Article contents
Nonlinear Bragg scattering of surface waves over a two-dimensional periodic structure
Published online by Cambridge University Press: 04 August 2022
Abstract
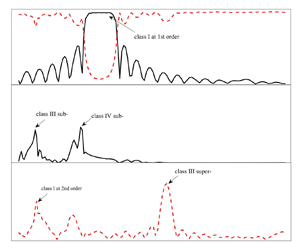
Bragg scattering of nonlinear surface waves over a wavy bottom is studied using two-dimensional fully nonlinear numerical wave tanks (NWTs). In particular, we consider cases of high nonlinearity which lead to complex wave generation and transformations, hence possible multiple Bragg resonances. The performance of the NWTs is well verified by benchmarking experiments. Classic Bragg resonances associated with second-order triad interactions among two surface (linear incident and reflected waves) and one bottom wave components (class I), and third-order quartet interactions among three surface (linear incident and reflected waves, and second-order reflected/transmitted waves) and one bottom wave components (class III) are observed. In addition, class I Bragg resonance occurring for the second-order (rather than linear) transmitted waves, and Bragg resonance arising from quintet interactions among three surface and two bottom wave components, are newly captured. The latter is denoted class IV Bragg resonance which magnifies bottom nonlinearity. It is also found that wave reflection and transmission at class III Bragg resonance have a quadratic rather than a linear relation with the bottom slope if the bottom size increases to a certain level. The surface wave and bottom nonlinearities are found to play opposite roles in shifting the Bragg resonance conditions. Finally, the results indicate that Bragg resonances are responsible for the phenomena of beating and parasitic beating, leading to a significantly large local free surface motion in front of the depth transition.
- Type
- JFM Papers
- Information
- Copyright
- © The Author(s), 2022. Published by Cambridge University Press
References
- 12
- Cited by





