Hostname: page-component-8448b6f56d-gtxcr Total loading time: 0 Render date: 2024-04-23T11:47:16.452Z Has data issue: false hasContentIssue false
  • English
  • Français

Flow structure on finite-span wings due to pitch-up motion

Published online by Cambridge University Press:  05 December 2011

T. O. Yilmaz  and
D. Rockwell
T. O. Yilmaz
Affiliation:
Department of Mechanical Engineering and Mechanics, Lehigh University, Bethlehem, PA 18018, USA
D. Rockwell*
Affiliation:
Department of Mechanical Engineering and Mechanics, Lehigh University, Bethlehem, PA 18018, USA
*
†Email address for correspondence: dor0@lehigh.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

The flow structure on low-aspect-ratio wings arising from pitch-up motion is addressed via a technique of particle image velocimetry. The objectives are to: determine the onset and evolution of the three-dimensional leading-edge vortex; provide complementary interpretations of the vortex structure in terms of streamlines, projections of spanwise and surface-normal vorticity, and surfaces of constant values of the second invariant of the velocity gradient tensor (iso-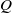 surfaces); and to characterize the effect of wing planform (rectangular versus elliptical) on this vortex structure. The pitch-up motion of the wing (plate) is from 0 to 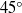over a time span corresponding to four convective time scales, and the Reynolds number based on chord is 10 000. Volumes of constant magnitude of the second invariant of the velocity gradient tensor are interpreted in conjunction with three-dimensional streamline patterns and vorticity projections in orthogonal directions. The wing motion gives rise to ordered vortical structures along its wing surface. In contrast to development of the classical two-dimensional leading-edge vortex, the flow pattern evolves to a strongly three-dimensional form at high angle of attack. The state of the vortex system, after attainment of maximum angle of attack, has a similar form for extreme configurations of wing planform. Near the plane of symmetry, a large-scale region of predominantly spanwise vorticity dominates. Away from the plane of symmetry, the flow is dominated by two extensive regions of surface-normal vorticity, i.e. swirl patterns parallel to the wing surface. This similar state of the vortex structure is, however, preceded by different sequences of events that depend on the magnitude of the spanwise velocity within the developing vortex from the leading edge of the wing. Spanwise velocity of the order of one-half the free stream velocity, which is oriented towards the plane of symmetry of the wing, results in regions of surface-normal vorticity. In contrast, if negligible spanwise velocity occurs within the developing leading-edge vortex, onset of the regions of surface-normal vorticity occurs near the tips of the wing. These extremes of large and insignificant spanwise velocity within the leading-edge vortex are induced respectively on rectangular and elliptical planforms.

JFM classification

Biological Fluid Dynamics: Swimming/flying Vortex Flows: Vortex dynamics
Type
Papers
Information
Journal of Fluid Mechanics , Volume 691 , 25 January 2012 , pp. 518 - 545
Copyright
Copyright © Cambridge University Press 2011

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1. Baik, Y. C., Bernal, L. P., Shyy, W. & Ol, M. V. 2011 Unsteady force generation and vortex dynamics of pitching and plunging flat plates at low Reynolds number. AIAA Paper 2011-220.CrossRefGoogle Scholar
2. Baik, Y. C., Rausch, J. M., Bernal, L. P. & Ol, M. V. 2009 Experimental investigation of pitching and plunging aerofoils at Reynolds number between and . AIAA Paper 2009-4030.CrossRefGoogle Scholar
3. Blondeaux, P., Fornarelli, F., Guglielmini, L., Triantafyllou, M. S. & Verzicco, R. 2005 Numerical experiments on flapping foils mimicking fish-like locomotion. Phys. Fluids 17, 113601.CrossRefGoogle Scholar
4. Bohl, D. G. & Koochesfahani, M. M. 2004 MTV measurements of axial flow in a concentrated vortex core. Phys. Fluids 16, 4185–4191.CrossRefGoogle Scholar
5. Brunton, S. L., Rowley, C. W., Taira, K., Colonius, T., Collins, J. & Williams, D. R. 2008 Unsteady aerodynamic forces on small-scale wings: experiments, simulations, and models. AIAA Paper 2008-520.CrossRefGoogle Scholar
6. Buchholz, J. H. J. & Smits, A. J. 2006 On the evolution of the wake structure produced by a low-aspect-ratio pitching panel. J. Fluid Mech. 546, 433–443.CrossRefGoogle Scholar
7. Buchner, A.-J, Buchmann, N. A. & Soria, J. 2010 Wake measurements of a pitching plate using multi-component, multi-dimensional PIV techniques. AFMC Paper 2010-221.Google Scholar
8. Carr, L. W. 1988 Progress in analysis and prediction of dynamics stall. J. Aircraft 25, 6–17.CrossRefGoogle Scholar
9. Cohn, R. K. & Koochesfahani, M. M. 1993 Effect of boundary conditions on axial flow in a concentrated vortex core. Phys. Fluids 5, 280–282.CrossRefGoogle Scholar
10. Dong, H., Mittal, R. & Najjar, F. M. 2006 Wake topology and hydrodynamic performance of low-aspect-ratio flapping foils. J. Fluid Mech. 566, 309–343.CrossRefGoogle Scholar
11. Eldredge, J. D., Wang, C. & Ol, M. V. 2009 A computational study of a canonical pitch-up, pitch-down wing maneuver. AIAA Paper 2009-3687.Google Scholar
12. Freymuth, P. 1989 Visualizing the connectivity of vortex systems for pitching wings. Trans. ASME: J. Fluids Engng 111, 217–220.Google Scholar
13. Geers, L. F. G., Tummers, M. J. & Hanjalic, K. 2005 Particle imaging velocimetry-based identification of coherent structures in normally impinging multiple jets. Phys. Fluids 17, 1–13.CrossRefGoogle Scholar
14. Granlund, K., Ol, M. V. & Bernal, L. 2011 Experiments on pitching plates: force and flow field measurements at low Reynolds numbers. AIAA Paper 2011-872.Google Scholar
15. Green, M. A., Rowley, C. W. & Haller, G. 2007 Detection of Lagrangian coherent structures in three-dimensional turbulence. J. Fluid Mech. 572, 111–120.CrossRefGoogle Scholar
16. Hill, M. J. M. 1894 On a spherical vortex. Phil. Trans. R. Soc. Lond. 185, 213–245.Google Scholar
17. Hunt, J. C. R., Wray, A. A. & Moin, P. 1988 Eddies, stream, and convergence zones in turbulent flows. Center for Turbulence Research Rep. CTR-S88.Google Scholar
18. Koochesfahani, M. M. 1989 Vortical patterns in the wake of an oscillating aerofoil. AIAA J. 27, 1200–1205.CrossRefGoogle Scholar
19. Lehmann, F. O. 2004 The mechanisms of lift enhancement in insect flight. Naturwissenschaften 91, 101–122.CrossRefGoogle ScholarPubMed
20. Lentink, D. & Dickinson, M. H. 2009 Rotational accelerations stabilize leading edge vortices on revolving fly wings. J. Expl Biol. 212, 2705–2719.CrossRefGoogle ScholarPubMed
21. McCroskey, W. J. 1982 Unsteady aerofoils. Annu. Rev. Fluid Mech. 14, 285–311.CrossRefGoogle Scholar
22. McCroskey, W. J., Carr, L. W. & McAlister, K. W. 1976 Dynamic stall experiments on oscillating aerofoils. AIAA J. 14, 57–63.CrossRefGoogle Scholar
23. Ohmi, K., Coutanceau, M., Daube, O. & Ta Phuoc, L. O. C. 1991 Further experiments on vortex formation around an oscillating and translating aerofoil at large incidences. J. Fluid Mech. 225, 607–630.CrossRefGoogle Scholar
24. Ol, M. V., Altman, A., Eldredge, J. D., Garmann, D. J. & Lian, Y. 2010 Résumé of the AIAA FDTC low Reynolds number discussion group’s canonical cases. AIAA Paper 2010-1085.CrossRefGoogle Scholar
25. Ol, M. V., Bernal, L., Kang, C. K. & Shyy, W. 2009 Shallow and deep dynamic stall for flapping low Reynolds number aerofoils. Exp. Fluids 46, 883–901.CrossRefGoogle Scholar
26. Parker, K., Von Ellenrieder, K. D. & Soria, J. 2005 Using stereo multi-grid DPIV measurements to investigate the vertical skeleton behind a finite-span flapping wing. Exp. Fluids 39, 281–298.CrossRefGoogle Scholar
27. Parker, K., Von Ellenrieder, K. D. & Soria, J. 2007 Morphology of the forced oscillatory flow past a finite-span wing at low Reynolds number. J. Fluid Mech. 571, 327–357.CrossRefGoogle Scholar
28. Prasad, A. K. 2000 Stereoscopic particle image velocimetry. Exp. Fluids 29, 103–116.CrossRefGoogle Scholar
29. Robinson, O. & Rockwell, D. 1993 Construction of three-dimensional images of flow structure via particle tracking techniques. Exp. Fluids 14, 257–270.CrossRefGoogle Scholar
30. Sane, S. P. 2003 The aerodynamics of insect flight. J. Expl Biol. 206, 4191–4208.CrossRefGoogle ScholarPubMed
31. Shyy, W., Aona, H., Chimakurthi, S. K., Trizila, P., Kang, C.-K., Cesnik, C. E. S. & Liu, H. 2010 Recent progress in flapping wing aerodynamics and aeroelasticity. Prog. Aerosp. Sci. 46, 284–327.CrossRefGoogle Scholar
32. Shyy, W., Lian, Y., Tang, J., Liu, H., Trizila, P., Stanford, B., Bernal, L., Cesnik, C., Friedmann, P. & Ifju, P. 2008 Computational aerodynamics of low Reynolds number plunging, pitching and flexible wings for MAV applications. Acta Mechanica Sin. 24, 351–373.CrossRefGoogle Scholar
33. Taira, K. & Colonius, T. 2009a Three-dimensional flows around low-aspect-ratio flat-plate wings at low Reynolds numbers. J. Fluid Mech. 623, 187–207.CrossRefGoogle Scholar
34. Taira, K. & Colonius, T. 2009b Effect of tip vortices in low-Reynolds number post stall flow control. AIAA J. 47, 749–756.CrossRefGoogle Scholar
35. Trizila, P., Kang, C.-K., Aono, H., Shyy, W. & Visbal, M. 2011 Low Reynolds aerodynamics of a flapping rigid flat plate. AIAA J. 49 (4), 806–823.CrossRefGoogle Scholar
36. Visbal, M. 2010 Numerical investigation of deep dynamic stall of a plunging aerofoil. AIAA Paper 2010-4458.CrossRefGoogle Scholar
37. Visbal, M. R. 2011 Three-dimensional flow structure on a heaving low-aspect-ratio wing. AIAA Paper 2011-219.CrossRefGoogle Scholar
38. Visbal, M., Gogineni, S. & Gaitonde, D. 1998 Direct numerical simulation of a forced transitional plane wall jet. AIAA Paper 1998-2643.CrossRefGoogle Scholar
39. Visbal, M. R. & Shang, J. S. 1989 Investigation of the flow structure around a rapidly pitching aerofoil. AIAA J. 27, 1044–1051.CrossRefGoogle Scholar
40. Von Ellenrieder, K. D., Parker, K. & Soria, J. 2003 Flow structures behind a heaving and pitching finite-span wing. J. Fluid Mech. 490, 129–138.CrossRefGoogle Scholar
41. Wang, Z. J. 2005 Dissecting insect flight. Annu. Rev. Fluid Mech. 37, 183–210.CrossRefGoogle Scholar
42. Yilmaz, T. O., Ol, M. & Rockwell, D. 2010 Scaling of flow separation on a pitching low aspect ratio plate. J. Fluids Struct. 26, 1034–1041.CrossRefGoogle Scholar
43. Yilmaz, T. O. & Rockwell, D. 2009 Three-dimensional flow structure on a maneuvering wing. Exp. Fluids 48, 539–544.CrossRefGoogle Scholar