No CrossRef data available.
Article contents
Experimental study of a single bubble's motion in a liquid metal under a horizontal magnetic field
Published online by Cambridge University Press: 31 May 2024
Abstract
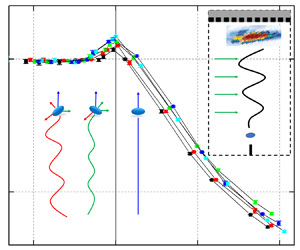
An ultrasonic phased array system is introduced to study the three-dimensional (3-D) movement of a single bubble in a GaInSn alloy under a transverse magnetic field (MF), which is verified by bubble experiments in water. The 3-D motion trajectories of individual bubbles in the GaInSn are obtained under a horizontal MF. As the MF becomes stronger, the bubble successively oscillates in random directions (R mode), a direction perpendicular to the MF (V mode), a direction parallel to the MF (P mode) and finally it rises straight (S mode). The significant anisotropy of the oscillation directions at a moderate MF intensity may be due to the anisotropy of the vortex structure around the bubble. Furthermore, the oscillation amplitude gradually declines with increasing MF intensity until the bubble trajectory finally becomes a straight line. Our measurements allow us to specify the characteristic regions for the observed bubble modes in the  $N-Eo-Re$ parameter space (N is the magnetic interaction parameter, Eo is the Eötvös number and Re is the Reynolds number). In addition, more detailed characteristics of bubble terminal velocity are revealed, showing that the bubble velocities are closely related to the motion modes. The increase in bubble velocity at a moderate MF intensity is caused by the weakening oscillation. At a high strength, the MF monotonically suppresses the rise velocity of the bubble with a fixed scaling law.
$N-Eo-Re$ parameter space (N is the magnetic interaction parameter, Eo is the Eötvös number and Re is the Reynolds number). In addition, more detailed characteristics of bubble terminal velocity are revealed, showing that the bubble velocities are closely related to the motion modes. The increase in bubble velocity at a moderate MF intensity is caused by the weakening oscillation. At a high strength, the MF monotonically suppresses the rise velocity of the bubble with a fixed scaling law.
JFM classification
- Type
- JFM Papers
- Information
- Copyright
- © The Author(s), 2024. Published by Cambridge University Press





