Hostname: page-component-77c89778f8-gq7q9 Total loading time: 0 Render date: 2024-07-19T01:56:35.093Z Has data issue: false hasContentIssue false
  • English
  • Français

The converging flow of viscoplastic fluid in a wedge or cone

Published online by Cambridge University Press:  17 March 2021

Jesse J. Taylor-West Open the ORCID record for Jesse J. Taylor-West [Opens in a new window]  and
Andrew J. Hogg Open the ORCID record for Andrew J. Hogg [Opens in a new window]
Jesse J. Taylor-West*
Affiliation:
School of Mathematics, University of Bristol, Woodland Road, BristolBS8 1UG, UK
Andrew J. Hogg
Affiliation:
School of Mathematics, University of Bristol, Woodland Road, BristolBS8 1UG, UK
*
†Email address for correspondence: j.taylor-west@bristol.ac.uk
Get access Rights & Permissions [Opens in a new window]

Abstract

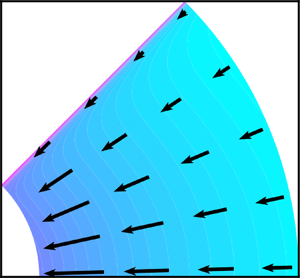
Converging flows of viscoplastic fluids, driven steadily through wedges and axisymmetric cones, are studied analytically and numerically. When the yield stress is relatively large, the bulk of the fluid flows plastically apart from within thin layers where the fluid is strongly sheared in order to achieve no slip at the boundary. Conversely, when the yield stress is relatively small, the motion is viscously dominated with weak corrections to the velocity and stress fields due to viscoplastic effects. For both regimes, viscoplasticity induces a weak angular velocity, directed away from the boundaries, and purely radial flow is not possible. The structure of the flow is calculated using asymptotic methods, confirmed by finite element numerical simulations. Flows of both Bingham and Herschel–Bulkley fluids are analysed, and both planar and axisymmetric geometries are considered. Although these cases differ in their details, they share the same qualitative structure. In particular, the viscoplastic boundary layers that emerge when the yield stress is relatively large, ensure not only that no slip is enforced, but also, through an intermediate matching layer, that the shear rates remain bounded.

JFM classification

Boundary Layers: Boundary layer structure Non-Newtonian Flows: Non-Newtonian Flows Low-Reynolds-number flows: Low-Reynolds-number flows
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 915 , 25 May 2021 , A69
Check for updates
Copyright
© The Author(s), 2021. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Ackerberg, R.C. 1965 The viscous incompressible flow inside a cone. J. Fluid Mech. 21 (1), 47–81.CrossRefGoogle Scholar
Alexandrov, S., Lyamina, E. & Mishuris, G. 2007 Flow of viscoplastic materials through converging channels. Proc. Appl. Maths Mech. 7 (1), 1060603–1060604.CrossRefGoogle Scholar
Alnæs, M.S., Blechta, J., Hake, J., Johansson, A., Kehlet, B., Logg, A., Richardson, C., Ring, J., Rognes, M.E. & Wells, G.N. 2015 The FEniCS project version 1.5. Arch. Numer. Softw. 3 (100), 9–23.Google Scholar
Ancey, C. 2007 Plasticity and geophysical flows: a review. J. Non-Newtonian Fluid Mech. 142 (1–3), 4–35.CrossRefGoogle Scholar
Ara, A., Khan, N., Sultan, F. & Ullah, S. 2019 Numerical simulation of Jeffery–Hamel flow of Bingham plastic fluid and heat transfer in the presence of magnetic field. Appl. Comput. Maths 18, 135–148.Google Scholar
Balmforth, N.J. & Craster, R.V. 1999 A consistent thin-layer theory for Bingham plastics. J. Non-Newtonian Fluid Mech. 84 (1), 65–81.CrossRefGoogle Scholar
Balmforth, N.J., Craster, R.V., Hewitt, D.R., Hormozi, S. & Maleki, A. 2017 Viscoplastic boundary layers. J. Fluid Mech. 813, 929–954.CrossRefGoogle Scholar
Balmforth, N.J., Frigaard, I.A. & Ovarlez, G. 2014 Yielding to stress: recent developments in viscoplastic fluid mechanics. Annu. Rev. Fluid Mech. 46 (1), 121–146.CrossRefGoogle Scholar
Banks, W.H.H., Drazin, P.G. & Zaturska, M.B. 1988 On perturbations of Jeffery–Hamel flow. J. Fluid Mech. 186, 559–581.CrossRefGoogle Scholar
Brewster, M.E., Chapman, S.J., Fitt, A.D. & Please, C.P. 1995 Asymptotics of slow flow of very small exponent power-law shear-thinning fluids in a wedge. Eur. J. Appl. Maths 6 (6), 559–571.CrossRefGoogle Scholar
Cristescu, N. 1975 Plastic flow through conical converging dies, using a viscoplastic constitutive equation. Intl J. Mech. Sci. 17 (6), 425–433.CrossRefGoogle Scholar
Dean, W.R. 1934 Note on the divergent flow of fluid. Lond. Edinb. Dubl. Phil. Mag. J. Sci. 18 (121), 759–777.CrossRefGoogle Scholar
Drazin, P.G. & Riley, N. 2006 The Navier–Stokes Equations: A Classification of Flows and Exact Solutions. Cambridge University Press.CrossRefGoogle Scholar
Durban, D. 1984 Rate effects in steady forming processes of plastic materials. Intl J. Mech. Sci. 26 (4), 293–304.CrossRefGoogle Scholar
Durban, D. 1985 On some simple steady forming process of viscoplastic solids. Acta Mechanica 57 (3), 123–141.CrossRefGoogle Scholar
Durban, D. 1986 On generalized radial flow patterns of viscoplastic solids with some applications. Intl J. Mech. Sci. 28 (2), 97–110.CrossRefGoogle Scholar
Fraenkel, L.E. 1962 Laminar flow in symmetrical channels with slightly curved walls. I. On the Jeffery–Hamel solutions for flow between plane walls. Proc. R. Soc. Lond. A 267 (1328), 119–138.Google Scholar
Frigaard, I.A., Paso, K. & de Souza Mendes, P.R. 2017 Bingham's model in the oil and gas industry. Rheol. Acta 56, 259–282.CrossRefGoogle Scholar
Hamel, G. 1917 Spiralförmige Bewegungen zäher Flüssigkeiten. Jahresbericht der Deutschen Mathematiker- Vereinigung 25, 34–60.Google Scholar
Harrison, W.J. 1919 The pressure in a viscous liquid moving through a channel with diverging boundaries. Proc. Camb. Phil. Soc. 19, 307–312.Google Scholar
Hill, R. 1950 The Mathematical Theory of Plasticity. Clarendon Press.Google Scholar
Hull, A.M. & Pearson, J.R.A. 1984 On the converging flow of viscoelastic fluids through cones and wedges. J. Non-Newtonian Fluid Mech. 14, 219–247.CrossRefGoogle Scholar
Jay, P., Magnin, A. & Piau, J.M. 2002 Numerical simulation of viscoplastic fluid flows through an axisymmetric contraction. Trans. ASME: J. Fluids Engng 124 (3), 700–705.Google Scholar
Jeffery, G.B. 1915 The two-dimensional steady motion of a viscous fluid. Lond. Edinb. Dubl. Phil. Mag. J. Sci. 29 (172), 455–465.CrossRefGoogle Scholar
Logg, A., Mardal, K.-A. & Wells, G.N. 2012 Automated Solution of Differential Equations by the Finite Element Method. Springer.CrossRefGoogle Scholar
Luu, L.-H., Philippe, P. & Chambon, G. 2015 Experimental study of the solid-liquid interface in a yield-stress fluid flow upstream of a step. Phys. Rev. E 91, 013013.CrossRefGoogle Scholar
Nadai, A. 1924 Über die Gleit- und Verzweigungsflächen einiger Gleichgewichtszustände bildsamer Massen und die Nachspannungen bleibend verzerrter Körper. Z. Phys. 30, 106–138.CrossRefGoogle Scholar
Nagler, J. 2017 Jeffery–Hamel flow of non-Newtonian fluid with nonlinear viscosity and wall friction. Z. Angew. Math. Mech. 38, 815–830.CrossRefGoogle Scholar
Oldroyd, J.G. 1947 Two-dimensional plastic flow of a Bingham solid: a plastic boundary-layer theory for slow motion. Math. Proc. Cambridge 43 (3), 383–395.CrossRefGoogle Scholar
Piau, J.-M. 2002 Viscoplastic boundary layer. J. Non-Newtonian Fluid Mech. 102 (2), 193–218.CrossRefGoogle Scholar
Piau, J.-M. & Debiane, K. 2004 The adhesive or slippery flat plate viscoplastic boundary layer for a shear-thinning power-law viscosity. J. Non-Newtonian Fluid Mech. 117 (2), 97–107.CrossRefGoogle Scholar
Rabideau, B.D., Moucheront, P., Bertrand, F., Rodts, S., Roussel, N., Lanos, C. & Coussot, P. 2010 The extrusion of a model yield stress fluid imaged by MRI velocimetry. J. Non-Newtonian Fluid Mech. 165 (7), 394–408.CrossRefGoogle Scholar
Rosenhead, L. 1940 The steady two-dimensional radial flow of viscous fluid between two inclined plane walls. Proc. R. Soc. Lond. A 175 (963), 436–467.Google Scholar
Sandru, N. & Camenshi, C. 1979 Viscoplastic flow through inclined planes with application to the strip drawing. Intl J. Engng Sci. 17 (6), 773–784.CrossRefGoogle Scholar
Saramito, P. 2016 Complex fluids: modeling and algorithms. In Viscoplastic Fluids, 91–142. Springer.CrossRefGoogle Scholar
Shield, R.T. 1955 Plastic flow in a converging conical channel. J. Mech. Phys. Solids 3 (4), 246–258.CrossRefGoogle Scholar
Tokpavi, D.L., Magnin, A. & Jay, P. 2008 Very slow flow of Bingham viscoplastic fluid around a circular cylinder. J. Non-Newtonian Fluid Mech. 154 (1), 65–76.CrossRefGoogle Scholar
Walton, I.C. & Bittleston, S.H. 1991 The axial flow of a Bingham plastic in a narrow eccentric annulus. J. Fluid Mech. 222, 39–60.CrossRefGoogle Scholar
Wildman, R.D., Blackburn, S., Benton, D.M., McNeil, P.A. & Parker, D.J. 1999 Investigation of paste flow using positron emission particle tracking. Powder Technol. 103 (3), 220–229.CrossRefGoogle Scholar