Hostname: page-component-8448b6f56d-cfpbc Total loading time: 0 Render date: 2024-04-24T06:54:30.564Z Has data issue: false hasContentIssue false
  • English
  • Français

Sojourn functionals for spatiotemporal Gaussian random fields with long memory

Part of: Geometric probability and stochastic geometry Limit theorems Stochastic processes

Published online by Cambridge University Press:  09 February 2023

N. N. Leonenko  and
M. D. Ruiz-Medina
N. N. Leonenko*
Affiliation:
Cardiff University
M. D. Ruiz-Medina*
Affiliation:
University of Granada
*
*Postal address: Cardiff University, Cardiff, Wales, UK. Email address: LeonenkoN@cardiff.ac.uk
**Postal address: University of Granada, Granada, Spain. Email address: mruiz@ugr.es
Get access Rights & Permissions [Opens in a new window]

Abstract

This paper addresses the asymptotic analysis of sojourn functionals of spatiotemporal Gaussian random fields with long-range dependence (LRD) in time, also known as long memory. Specifically, reduction theorems are derived for local functionals of nonlinear transformation of such fields, with Hermite rank 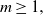$m\geq 1,$ under general covariance structures. These results are proven to hold, in particular, for a family of nonseparable covariance structures belonging to the Gneiting class. For 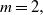$m=2,$ under separability of the spatiotemporal covariance function in space and time, the properly normalized Minkowski functional, involving the modulus of a Gaussian random field, converges in distribution to the Rosenblatt-type limiting distribution for a suitable range of values of the long-memory parameter.

Keywords

Asymptotic normalityexcursion setsLRDRosenblatt-type distributionspatiotemporal random fields

MSC classification

Primary: 60G60: Random fields 60G15: Gaussian processes 60F05: Central limit and other weak theorems
Secondary: 60D05: Geometric probability and stochastic geometry
Type
Original Article
Information
Journal of Applied Probability , Volume 60 , Issue 1 , March 2023 , pp. 148 - 165
Check for updates
Copyright
© The Author(s), 2023. Published by Cambridge University Press on behalf of Applied Probability Trust

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Adler, R. J. and Taylor, J. E. (2007). Random Fields and Geometry. Springer, New York.Google Scholar
Aharonyan, N. G. and Khalatyan, V. (2020). Distribution of the distance between two random points in a body from $\mathbb{R}^{n}.$ J. Contemp. Math. Anal. 55, 329–334.Google Scholar
Armstrong, R. T. et al. (2018). Porous media characterization using Minkowski functionals: theories, applications and future directions. Transport Porous Media 130, 305–335.CrossRefGoogle Scholar
Azaïs, J.-M. and Wschebor, M. (2009). Level Sets and Extrema of Random Processes and Fields. John Wiley, Hoboken.CrossRefGoogle Scholar
Berman, S. M. (1979). High level sojourns for strongly dependent Gaussian processes. Z. Wahrscheinlichkeitsth. 50, 223–236.CrossRefGoogle Scholar
Bulinski, A., Spodarev, E. and Timmermann, F. (2012). Central limit theorems for the excursion volumes of weakly dependent random fields. Bernoulli 18, 100–118.CrossRefGoogle Scholar
Christakos, G. (2000). Modern Spatiotemporal Geostatistics. Oxford University Press.Google Scholar
Cressie, N. and Huang, H. C. (1999). Classes of nonseparable, spatio-temporal stationary covariance functions. J. Amer. Statist. Assoc. 94, 1330–1340.CrossRefGoogle Scholar
Dobrushin, R. L. and Major, P. (1979). Non-central limit theorem for non-linear functionals of Gaussian fields. Z. Wahrscheinlichkeitsth. 50, 1–28.CrossRefGoogle Scholar
Erdélyi, A., Magnus, W., Obergettinger, F. and Tricomi, F. G. (1955). Higher Tran-scendental Functions, Vol. 3. McGraw-Hill, New York.Google Scholar
Estrade, A. and León, J. R. (2016). A central limit theorem for the Euler characteristic of a Gaussian excursion set. Ann. Prob. 44, 3849–3878.CrossRefGoogle Scholar
Feller, W. (1971). An Introduction to Probability Theory and Its Applications, Vol. 2. John Wiley, New York.Google Scholar
Gneiting, T. (2002). Nonseparable, stationary covariance functions for space–time data. J. Amer. Statist. Assoc. 97, 590–600.CrossRefGoogle Scholar
Gregorová, E. et al. (2018). Microstructure characterization of mullite foam by image analysis, mercury porosimetry and X-ray computed microtomography. Ceramics Internat. 44, 12315–12328.CrossRefGoogle Scholar
Haubold, H. J, Mathai, A. M. and Saxena, R. K. (2011). Mittag-Leffler functions and their applications. J. Appl. Math. 2011, article no. 2986285, 51 pp. Available at http://dx.doi.org/10.1155/2011/298628.CrossRefGoogle Scholar
Ivanov, A. V. and Leonenko, N. N. (1989). Statistical Analysis of Random Fields. Kluwer Academic, Dordrecht.CrossRefGoogle Scholar
Ivonin, D., Kalnin, T., Grachev, E. and Shein, E. (2020). Quantitative analysis of pore space structure in dry and wet soil by integral geometry methods. Geosci. 10, article no. 365.CrossRefGoogle Scholar
Kratz, M. F. and León, J. R. (1997). Hermite polynomial expansion for non-smooth functionals of stationary Gaussian processes: crossings and extremes. Stoch. Process. Appl. 66, 237–252.CrossRefGoogle Scholar
Kratz, M. F. and León, J. R. (2001). Central limit theorems for level functionals of stationary Gaussian processes and fields. J. Theoret. Prob. 14, 639–672.CrossRefGoogle Scholar
Lellouche, S. and Souris, M. (2020). Distribution of distances between elements in a compact set. Stats 3, 1–15.CrossRefGoogle Scholar
Leonenko, N. N. (1999). Limit Theorems for Random Fields with Singular Spectrum. Kluwer Academic, Dordrecht.CrossRefGoogle Scholar
Leonenko, N. N. and Olenko, A. (2014). Sojourn measures of Student and Fisher–Snedecor random fields. Bernoulli 20, 1454–1483.CrossRefGoogle Scholar
Leonenko, N. N. and Olenko, A. (2013). Tauberian and Abelian theorems for long-range dependent random fields. Methodology Comput. Appl. Prob. 15, 715–742.CrossRefGoogle Scholar
Leonenko, N. N. and Ruiz-Medina, M. D. (2017). Increasing domain asymptotics for the first Minkowski functional of spherical random fields. Theory Prob. Math. Statist. 97, 120–141.Google Scholar
Leonenko, N. N., Ruiz-Medina, M. D. and Taqqu, M. S. (2017). Non-central limit theorems for random fields subordinated to gamma-correlated random fields. Bernoulli 23, 3469–3507.CrossRefGoogle Scholar
Leonenko, N. N., Ruiz-Medina, M. D. and Taqqu, M. S. (2017). Rosenblatt distribution subordinated to Gaussian random fields with long-range dependence. Stoch. Anal. Appl. 35, 144–177.CrossRefGoogle Scholar
Linde, A. and Mukhanov, V. F. (1997). Non-Gaussian isocurvature perturbations from inflation. Phys. Rev. D 56, R535–R539.CrossRefGoogle Scholar
Lord, R. D. (1954). The distribution of distance in a hypersphere. Ann. Math. Statist. 25, 794–798.CrossRefGoogle Scholar
Major, P. (1981). Multiple Wiener–Itô Integrals. Springer, Cham.CrossRefGoogle Scholar
Makogin, V. and Spodarev, E. (2022). Limit theorems for excursion sets of subordinated Gaussian random fields with long-range dependence. Stochastics 94, 111–142.CrossRefGoogle Scholar
Marinucci, D. and Peccati, G. (2011). Random Fields on the Sphere: Representation, Limit Theorems and Cosmological Applications. Cambridge University Press.CrossRefGoogle Scholar
Marinucci, D., Rossi, M. and Vidotto, A. (2020). Non-universal fluctuations of the empirical measure for isotropic stationary fields on $\mathbb{S}^{2}\times \mathbb{R}.$ Ann. Appl. Prob. 31, 2311–2349.Google Scholar
Marinucci, D. and Vadlamani, S. (2013). High-frequency asymptotics for Lipschitz–Killing curvatures of excursion sets on the sphere. Ann. Appl. Prob. 26, 462–506.Google Scholar
Mosser, L., Dubrule, O. and Blunt, M. J. (2017). Reconstruction of three-dimensional porous media using generative adversarial neural networks Phys. Rev. E 96, 043309.Google Scholar
Novikov, D., Schmalzing, J. and Mukhanov, V. F. (2000). On non-Gaussianity in the cosmic microwave background. Astronom. Astrophys. 364, 17–25.Google Scholar
Pabst, W., Uhlrová, T. and Gregorová, E. (2028). Microstructure characterization of porous ceramics via Minkowski functionals. In Proc. 12th Pacific Rim Conference on Ceramic and Glass Technology (Ceramic Transactions 264), John Wiley, Hoboken, pp. 53–64.Google Scholar
Peccati, G. and Taqqu, M. S. (2011). Wiener Chaos: Moments, Cumulants and Diagrams. Springer, New York.CrossRefGoogle Scholar
Pyrcz, M. J. and Deutsch, C. V. (2014). Geostatistical Reservoir Modeling. Oxford University Press.Google Scholar
Simon, T. (2014). Comparing Fréchet and positive stable laws. Electron. J. Prob. 19, 25 pp.CrossRefGoogle Scholar
Steele, J. H. (2007). Characterizing 3D microstructure using the Minkowski functionals. Microsc. Microanal. 13, 1658–1659.CrossRefGoogle Scholar
Taqqu, M. S. (1975). Weak convergence to fractional Brownian motion and to the Rosenblatt process. Z. Wahrscheinlichkeitsth. 31, 287–302.CrossRefGoogle Scholar
Taqqu, M. S. (1979). Convergence of integrated processes of arbitrary Hermite rank. Z. Wahrscheinlichkeitsth. 50, 53–83.CrossRefGoogle Scholar
Tsukanov, A. et al. (2020). Effect of cold-sintering parameters on structure, density, and topology of Fe–Cu nanocomposites. Materials 13, article no. 541, 19 pp.CrossRefGoogle ScholarPubMed