Hostname: page-component-848d4c4894-jbqgn Total loading time: 0 Render date: 2024-06-25T17:46:17.412Z Has data issue: false hasContentIssue false
  • English
  • Français

Recursive estimation of distributional fix-points

Part of: Sequential methods Special processes Stochastic analysis Applications

Published online by Cambridge University Press:  14 July 2016

Paul Embrechts  and
Harro Walk
Paul Embrechts*
Affiliation:
ETH Zürich
Harro Walk*
Affiliation:
Universität Stuttgart
*
∗Postal address: Department of Mathematics, ETH, CH-8092 Zürich, Switzerland. Email address: embrecht@math.ethz.ch
∗∗Postal address: Mathematisches Institut A, Universität Stuttgart, 70550 Stuttgart, Germany. Email address: walk@mathematik.uni-stuttgart.de
Get access Rights & Permissions [Opens in a new window]

Abstract

In various stochastic models the random equation 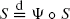of implicit renewal theory appears where the real random variable S and the stochastic process Ψ with index space and state space R are independent. By use of stochastic approximation the distribution function of S is recursively estimated on the basis of independent or ergodic copies of Ψ. Under integrability assumptions almost sure L1-convergence is proved. The choice of gains in the recursion is discussed. Applications are given to insurance mathematics (perpetuities) and queueing theory (stationary waiting and queueing times).

Keywords

Random equationdistributional fix-pointrecursive estimationstochastic approximationinsurancestochastic discountingperpetuityqueueing theoryG/G/1stationary waiting timestationary queueing time

MSC classification

Primary: 62L20: Stochastic approximation
Secondary: 60H25: Random operators and equations 62P05: Applications to actuarial sciences and financial mathematics 60K25: Queueing theory
Type
Research Papers
Information
Journal of Applied Probability , Volume 37 , Issue 1 , March 2000 , pp. 73 - 87
Copyright
Copyright © 2000 by The Applied Probability Trust 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Aebi, M., Embrechts, P., and Mikosch, T. (1994). Stochastic discounting, aggregate claims and the bootstrap. Adv. Appl. Prob. 26, 183–206.Google Scholar
Embrechts, P., and Goldie, C. M. (1994). Perpetuities and random equations. In Asymptotic Statistics: Proc. Fifth Prague Symp., September 1993, eds. Mandl, P. and Huskova, M. Physica-Verlag, Heidelberg, pp. 75–86.Google Scholar
Embrechts, P., Klueppelberg, C., and Mikosch, T. (1997). Modelling Extremal Events for Insurance and Finance. Springer, Berlin.Google Scholar
Fabian, V. (1968). On asymptotic normality in stochastic approximation. Ann. Math. Statist. 39, 1327–1332.Google Scholar
Goldie, C. M. (1991). Implicit renewal theory and tails of solutions of random equations. Ann. Appl. Prob. 1, 126–166.CrossRefGoogle Scholar
Goldie, C. M. and Grübel, R. (1996). Perpetuities with thin tails. Adv. Appl. Prob. 28, 463–480.Google Scholar
Györfi, L., and Masry, E. (1990). The L 1 and L 2 strong consistency of recursive kernel density estimation from dependent samples. IEEE Trans. Inf. Theory IT 36, 531–539.Google Scholar
Kesten, H. (1973). Random difference equations and renewal theory for products of random matrices. Acta Math. 131, 207–248.Google Scholar
Krengel, U. (1985). Ergodic Theorems. De Gruyter, Berlin.Google Scholar
Landers, D., and Rogge, L. (1978). An ergodic theorem for Fréchet-valued random variables. Proc. Amer. Math. Soc. 72, 49–53.Google Scholar
Letac, G. (1986). A contraction principle for certain Markov chains and its applications. In Random Matrices and their Applications (Contemp. Math. 50), eds. Cohen, J. E., Kesten, H. and Newman, C. M. Amer. Math. Soc., Providence, RI, pp. 263–273.Google Scholar
Ljung, L., Pflug, G., and Walk, H. (1992). Stochastic Approximation and Optimization of Random Systems. Birkhäuser, Basel.Google Scholar
Ljung, L. and Söderström, I. (1983). Theory and Practice of Recursive Identification. MIT Press, Cambridge, MA.Google Scholar
Polyak, B. T. (1990). New method of stochastic approximation type. Automat. Remote Control 51, 937–946.Google Scholar
Polyak, B. T., and Juditsky, A. B. (1992). Acceleration of stochastic approximation by averaging. SIAM J. Control and Optimization 30, 838–855.CrossRefGoogle Scholar
Polyak, B. T. and Tsypkin, Ya. Z. (1979). Adaptive estimation algorithms (convergence, optimality, stability). Automat. Remote Control 40, 378–389.Google Scholar
Reed, M., and Simon, B. (1980). Methods of Modern Mathematical Physics, Vol. I, Functional Analysis. Academic Press, New York.Google Scholar
Robbins, H., and Siegmund, D. (1971). A convergence theorem for nonnegative almost supermartingales and some applications. In Optimizing Methods in Statistics, ed. Rustagi, J.S. Academic Press, New York, pp. 233–257.Google Scholar
Ruppert, D. (1991). Stochastic approximation. In Handbook of Sequential Analysis, eds. Gosh, B. K. and Sen, P. K. Marcel Dekker, New York, pp. 503–529.Google Scholar
Tempel'man, A. A. (1972). Ergodic theorems for general dynamical systems. Trans. Moscow Math. Soc. 26, 94–132.Google Scholar
Thavaneswaran, A., and Abraham, B. (1988). Estimation for nonlinear time series models using estimating equations. J. Time Ser. Anal. 9, 99–108.Google Scholar
Venter, J. H. (1967). An extension of the Robbins–Monro procedure. Ann. Math. Statist. 38, 181–190.CrossRefGoogle Scholar
Vervaat, W. (1979). On a stochastic difference equation and representation of non-negative infinitely divisible random variables. Adv. Appl. Prob. 11, 750–783.Google Scholar
Walk, H. (1988). Limit behaviour of stochastic approximation processes. Statistics & Decisions 6, 109–128.Google Scholar
Walk, H. and Zsidó, L. (1989). Convergence of the Robbins–Monro method for linear problems in a Banach space. J. Math. Anal. Appl. 139, 152–177.Google Scholar
Wei, C. Z. (1987). Multivariate adaptive stochastic approximation. Ann. Statist. 15, 1115–1130.Google Scholar