Hostname: page-component-76fb5796d-5g6vh Total loading time: 0 Render date: 2024-04-27T23:01:03.776Z Has data issue: false hasContentIssue false
  • English
  • Français

Queues with time-dependent arrival rates I—the transition through saturation

Published online by Cambridge University Press:  14 July 2016

G. F. Newell
G. F. Newell*
Affiliation:
Institute of Transportation and Traffic Engineering, University of California, Berkeley
Get access Rights & Permissions [Opens in a new window]

Abstract

Suppose that the arrival rate λ(t) of customers to a service facility increases with time at a nearly constant rate, dλ(t)/dt = a, so as to pass through the saturation condition, λ(t) = μ = service capacity, at some time which we label as t = 0. The stochastic properties of the queue are investigated here through use of the diffusion approximation (Fokker-Planck equation). 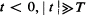It is shown that there is a characteristic time Tproportional to α–2/3 such that if , then the queue distribution stays close to the prevailing equilibrium distribution associated with the λ(t) and μ, evaluated at time t. For |t| = O(T), however, the mean queue length is much less than the equilibrium mean, and is measured in units of some characteristic length L which is proportional to α–1/3. For 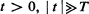, the queue is approximately normally distributed with a mean of the order L larger than that predicted by deterministic queueing models. Numerical estimates are given for the mean and variance of the distribution for all t. The queue distributions are also evaluated in non-dimensional units.

Type
Research Papers
Information
Journal of Applied Probability , Volume 5 , Issue 2 , August 1968 , pp. 436 - 451
Copyright
Copyright © Applied Probability Trust 1968 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1] Oliver, R. M. and Samuel, A. H. (1962) Reducing letter delays in post offices. Operat. Res. 10, 839–892.Google Scholar
[2] Gazis, D. C. and Potts, R. B. (1963) The oversaturated intersection. 2nd International Symposium on the Theory of Traffic Flow, London, OECD Paris 1965, 221–237.Google Scholar
[3] May, A. D. and Keller, H. E. M. (1967) A deterministic queueing model. Transportation Res. 1, 117–128.Google Scholar
[4] Kingman, J. F. C. (1965) The heavy traffic approximation in the theory of queues. Proc. Symposium on Congestion Theory, Smith, W. L. and Wilkinson, W. E. (eds.), Univ. of North Carolina Monograph Series in Probability and Statistics.Google Scholar
[5] Newell, G. F. (1965) Approximate methods for queues with application to the fixed-cycle traffic light. SIAM Rev. 7, 223–240.Google Scholar
[6] Cox, D. R. and Miller, H. D. (1965) The Theory of Stochastic Processes. Chapter 5. John Wiley & Sons, New York.Google Scholar
[7] Cox, D. R. and Smith, W. L. (1961). Queues. Methuen, London.Google Scholar
[8] Gaver, D. P. (1968) Diffusion approximation and models for certain congestion problems. (In press).Google Scholar