Hostname: page-component-848d4c4894-cjp7w Total loading time: 0 Render date: 2024-06-20T22:08:20.251Z Has data issue: false hasContentIssue false
  • English
  • Français

On the probability of covering the circle by random arcs

Published online by Cambridge University Press:  14 July 2016

F. W. Huffer  and
L. A. Shepp
F. W. Huffer*
Affiliation:
Florida State University
L. A. Shepp*
Affiliation:
AT & T Bell Laboratories
*
∗Postal address: Department of Statistics, Florida State University, Tallahassee, FL 32306-3033, USA.
∗∗Postal address: AT & T Bell Laboratories, 600 Mountain Avenue, Murray Hill, NJ 07974, USA.
Get access Rights & Permissions [Opens in a new window]

Abstract

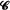Arcs of length lk, 0 < lk < 1, k = 1, 2, ···, n, are thrown independently and uniformly on a circumference having unit length. Let P(l1, l2, · ··, ln) be the probability that 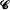is completely covered by the n random arcs. We show that P(l1, l2,· ··, ln) is a Schur-convex function and that it is convex in each argument when the others are held fixed.

Keywords

COVERAGE PROBABILITIESSCHUR-CONVEXGEOMETRICAL PROBABILITY
Type
Research Papers
Information
Journal of Applied Probability , Volume 24 , Issue 2 , June 1987 , pp. 422 - 429
Copyright
Copyright © Applied Probability Trust 1987 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

Research supported by Office of Naval Research Contract N00014-76-C-0475.

References

Huffer, F. W. (1987) Inequalities for the M/G/∞ queue and related shot noise processes. J. Appl. Prob. 24(4).CrossRefGoogle Scholar
Huffer, F. W. (1986) Variability orderings related to coverage problems on the circle. J. Appl. Prob. 23, 97–106.Google Scholar
Janson, S. (1983) Random coverings of the circle with arcs of random lengths. In Probability and Mathematical Statistics: Essays in Honour of Carl-Gustav Esseen, ed. Gut, A. and Holst, L. Department of Mathematics, Uppsala University, Sweden.Google Scholar
Marshall, A. W. and Olkin, I. (1979) Inequalities: Theory of Majorization and Its Applications. Academic Press, New York.Google Scholar
Shepp, L. A. (1972) Covering the circle with random arcs. Israel J. Math. 11, 328–345.Google Scholar
Siegel, A. F. and Holst, L. (1982) Covering the circle with random arcs of random sizes. J. Appl. Prob. 19, 373–381.Google Scholar
Solomon, H. (1978) Geometric Probability. SIAM, Philadelphia, PA.CrossRefGoogle Scholar
Stevens, W. L. (1939) Solution to a geometrical problem in probability. Ann. Eugenics 9, 315–320.CrossRefGoogle Scholar
Wschebor, M. (1973) Sur le recouvrement du cercle par des ensembles placés au hasard. Israel J. Math. 15, 1–11.Google Scholar