Hostname: page-component-848d4c4894-tn8tq Total loading time: 0 Render date: 2024-07-04T16:04:09.531Z Has data issue: false hasContentIssue false
  • English
  • Français

On the critical infection rate of the one-dimensional basic contact process: numerical results

Published online by Cambridge University Press:  14 July 2016

Herbert Ziezold  and
Christian Grillenberger
Herbert Ziezold*
Affiliation:
Gesamthochschule Kassel
Christian Grillenberger*
Affiliation:
Gesamthochschule Kassel
*
∗ Postal address: Gesamthochschule Kassel, FB 17 Mathematik, Postf. 101380, 3500 Kassel, W. Germany.
∗ Postal address: Gesamthochschule Kassel, FB 17 Mathematik, Postf. 101380, 3500 Kassel, W. Germany.
Get access Rights & Permissions [Opens in a new window]

Abstract

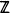Instead of the basic contact process on with infection rate λ we consider for m ≧ 0 the Markov process starting with ξ0(k) = 1 for k ≧ 0 and ξ0(k)= 0 for k < 0 and with changing only those k which are at most m places to the right of the left-most infected cell. For m = 0, 1,· ··, 14 direct computations give critical values which are lower bounds for the critical value of the original basic contact process.

Keywords

COUPLED PROCESSESCRITICAL VALUEINTERACTING PARTICLE SYSTEM
Type
Research Papers
Information
Journal of Applied Probability , Volume 25 , Issue 1 , March 1988 , pp. 1 - 8
Copyright
Copyright © Applied Probability Trust 1988 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1] Brower, R. C., Furman, M. A., and Moshe, M. (1978) Critical exponents for the reggeon quantum spin model. Phys. Lett. B 76, 213–219.Google Scholar
[2] Dobrushin, R. L. (1971) Markov processes with a large number of locally interacting components: existence of a limit process and its ergodicity. Probl. Inf. Trans. 7, 149–164.Google Scholar
[3] Durrett, R. (1980) On the growth of one-dimensional contact processes. Ann. Prob. 8, 890–907.Google Scholar
[4] Durrett, R. and Griffeath, D. (1983) Supercritical contact processes on Z. Ann. Prob. 11, 1–15.CrossRefGoogle Scholar
[5] Gray, L. and Griffeath, D. (1982) A stability criterion for attractive nearest-neighbor spin systems on Z. Ann. Prob. 10, 67–85.Google Scholar
[6] Griffeath, D. (1975) Ergodic theorems for graph interactions. Adv. Appl. Prob. 7, 179–194.Google Scholar
[7] Griffeath, D. (1979) Pointwise ergodicity of the basic contact process. Ann. Prob. 7, 139–143.CrossRefGoogle Scholar
[8] Griffeath, D. (1981) The basic contact process. Stock. Proc. Appl. 11, 151–186.Google Scholar
[9] Griffeath, D. and Liggett, T. M. (1982) Critical phenomena for Spitzer's reversible nearest-particle systems. Ann. Prob. 10, 881–895.Google Scholar
[10] Harris, T. E. (1974) Contact interactions on a lattice. Ann. Prob. 2, 969–988.Google Scholar
[11] Holley, R. and Liggett, T. M. (1978) The survival of contact processes. Ann. Prob. 6, 198–206.Google Scholar
[12] Liggett, T. M. (1972) Existence theorems for infinite particle systems. Trans. Amer. Math. Soc. 165, 471–481.CrossRefGoogle Scholar
[13] Liggett, T. M. (1985) Interacting Particle Systems. Springer-Verlag, New York.Google Scholar
[14] Richardson, D. (1973) Random growth in a tesselation. Proc. Camb. Phil. Soc. 74, 515–528.Google Scholar
[15] Schürger, K. and Tautu, P. (1976) A Markovian configuration model for carcinogenesis. In Mathematical Models in Medicine. Lecture Notes in Biomathematics 11, Springer-Verlag, Berlin.Google Scholar
[16] Spitzer, F. (1971) Random Fields and Interacting Particle Systems . Mathematical Association of America, Washington.Google Scholar