Article contents
On an inequality of Heyde
Published online by Cambridge University Press: 14 July 2016
Extract
In [3] Heyde proposed an extended version of the well-known Hájek-Rényi inequality to include random variables without finite moments. The purpose of this note is to point out that the theorem in [3] is in error, and to prove the following theorem in its stead:
Theorem. Let X1, X2, ··· be any sequence of random variables, and define 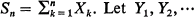 be independent random variables, each with mean zero and finite variance, and define Zk = Xk - Yk for k ≧ 1. Let c1, c2, ··· be a non-increasing sequence of positive numbers.
be independent random variables, each with mean zero and finite variance, and define Zk = Xk - Yk for k ≧ 1. Let c1, c2, ··· be a non-increasing sequence of positive numbers.
- Type
- Short Communications
- Information
- Copyright
- Copyright © Applied Probability Trust 1970
References
- 1
- Cited by




