Hostname: page-component-7479d7b7d-pfhbr Total loading time: 0 Render date: 2024-07-12T12:35:16.688Z Has data issue: false hasContentIssue false
  • English
  • Français

Modelling hierarchical systems by a continuous-time homogeneous Markov chain using two-wave panel data

Part of: Applications Markov processes Nonparametric inference Inference from stochastic processes

Published online by Cambridge University Press:  14 July 2016

Philippe Carette
Philippe Carette*
Affiliation:
Vrije Universiteit Brussel
*
∗Postal address: Center for Manpower Planning, Pleinlaan 2, B-1050 Brussel, Belgium. Email address: phcarett@vub.ac.be.
Get access Rights & Permissions [Opens in a new window]

Abstract

An open hierarchical (manpower) system divided into a totally ordered set of k grades is discussed. The transitions occur only from one grade to the next or to an additional (k+1)th grade representing the external environment of the system. The model used to describe the dynamics of the system is a continuous-time homogeneous Markov chain with k+1 states and infinitesimal generator R = (rij) satisfying rij = 0 if i > j or i + 1 < j ≤ k (i, j = 1,…,k+1), the transition matrix P between times 0 and 1 being P = expR. In this paper, two-wave panel data about the hierarchical system are considered and the resulting fact that, in general, the maximum-likelihood estimated transition matrix 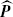cannot be written as an exponential of an infinitesimal generator R having the form described above. The purpose of this paper is to investigate when this can be ascribed to the effect of sampling variability.

Keywords

Continuous-time Markov chainembedding problemstochastic matrixpanel datainference

MSC classification

Primary: 60J27: Continuous-time Markov processes on discrete state spaces 62M02: Markov processes
Secondary: 62G10: Hypothesis testing 62P25: Applications to social sciences
Type
Research Papers
Information
Journal of Applied Probability , Volume 36 , Issue 3 , September 1999 , pp. 644 - 653
Copyright
Copyright © Applied Probability Trust 1999 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bartholomew, D. J. (1982). Stochastic Models for Social Processes, 3rd edn. Wiley, Chichester.Google Scholar
Bartholomew, D., Forbes, A., and McClean, S. (1991). Statistical Techniques for Manpower Planning. Wiley, Chichester.Google Scholar
Bishop, Y. M. M., Fienberg, F. F., and Holland, P. W. (1975). Discrete Multivariate Analysis. MIT Press, Cambridge, MA.Google Scholar
Carette, P. (1995). Characterizations of embeddable 3 × 3 stochastic matrices with a negative eigenvalue. New York J. Math. 1, 120–129.Google Scholar
Carette, P. (1997). New results on the embedding problem of homogeneous Markov chains with finitely many states. , Vrije Universiteit Brussel.Google Scholar
Carette, P. (1998). Compatibility of multi-wave panel data and the continuous-time homogeneous Markov chain. Appl. Stoch. Models Data Anal. 14, 219–228.Google Scholar
Cohen, J. E., and Singer, B. (1979). Malaria in Nigeria: constrained continuous-time Markov models for discrete-time longitudinal data on human mixed-species interactions. Lect. Math. Life Sci. 12, 69–133.Google Scholar
Cuthbert, J. R. (1973). The logarithm function for finite-state Markov semi-groups. J. London Math. Soc. 6, 524–532.Google Scholar
Elfving, G. (1937). Zur Theorie der markoffschen Ketten. Acta Soc. Sci. Fennicae n. Ser. A2.Google Scholar
Freedman, D. (1971). Markov Chains. Holden-Day, San Francisco.Google Scholar
Frydman, H. (1980). The embedding problem for Markov chains with three states. Math. Proc. Camb. Phil. Soc. 87, 285–294.Google Scholar
Frydman, H. (1983). On a number of poisson matrices in bang-bang representations for 3 × 3 embeddable matrices. J. Multivariate Anal. 13, 464–472.CrossRefGoogle Scholar
Frydman, H., and Singer, B. (1979). Total positivity and the embedding problem for Markov chains. Math. Proc. Camb. Phil. Soc. 86, 339–344.Google Scholar
Gantmacher, F. R. (1960). The Theory of Matrices, Vol. 1. Chelsea, New York.Google Scholar
Goodman, G. S. (1970). An intrinsic time for non-stationary finite Markov chains. Z. Wahrscheinlichkeitsth. 16, 165–180.Google Scholar
Johansen, S. (1973). A central limit theorem for finite semi-groups and its application to the imbedding problem for finite-state Markov chains. Z. Wahrscheinlichkeitsth. 26, 171–190.Google Scholar
Johansen, S. (1974). Some results on the imbedding problem for finite Markov chains. J. London Math. Soc. 8, 345–351.Google Scholar
Johansen, S., and Ramsey, F. L. (1979). A bang-bang representation for 3 × 3 embeddable stochastic matrices. Z. Wahrscheinlichkeitsth. 47, 107–118.Google Scholar
Kingman, J. F. C. (1962). The imbedding problem for finite Markov chains. Z. Wahrscheinlichkeitsth. 1, 14–24.Google Scholar
McClean, S., and Devine, C. (1995). A nonparametric maximum likelihood estimator for incomplete renewal data. Biometrika 82, 791–803.Google Scholar
McClean, S. I., and Montgomery, E. (1995). Estimation for continuous-time non-homogeneous Markov and semi-Markov manpower models. In Proc. 7th Internat. Symp. Applied Stochastic Models and Data Analysis, ed. Janssen, J. and McClean, S. University of Ulster, Northern Ireland, pp. 384–395.Google Scholar
Singer, B., and Cohen, J. E. (1980). Estimating malaria incidence and recovery rates from panel surveys. Math. Biosci. 49, 273–305.Google Scholar
Singer, B., and Spilerman, S. (1976). The representation of social processes by Markov models. Amer. J. Sociol. 82, 1–54.Google Scholar
Singer, B., and Spilerman, S. (1977). Fitting stochastic models to longitudinal survey data – some examples in the social sciences. Bull. Int. Statist. Inst. 47, 283–300.Google Scholar
Speakman, J. M. O. (1967). Two Markov chains with a common skeleton. Z. Warscheinlichkeitsth. 7, 224.Google Scholar