Hostname: page-component-848d4c4894-8bljj Total loading time: 0 Render date: 2024-06-26T09:09:57.619Z Has data issue: false hasContentIssue false
  • English
  • Français

Mean-square and almost-sure convergence of supercritical age-dependent branching processes

Published online by Cambridge University Press:  14 July 2016

Edgar Z. Ganuza  and
S. D. Durham
Edgar Z. Ganuza
Affiliation:
University of South Carolina
S. D. Durham
Affiliation:
University of South Carolina
Get access Rights & Permissions [Opens in a new window]

Abstract

Letting Z(t) be the number of objects alive at time t in a general supercritical age-dependent branching process generated by a single ancestor born at time 0, one achieves (Theorem 1) mean-square convergence of Z(t)/E[Z(t)] provide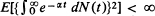d and 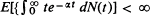, where N(t) is the number of offspring of the initial ancestor born by time t and α is the (positive) Malthusian parameter defined by 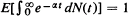. If the stronger conditions that (Theorem 2) 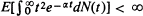and hold also, then the convergence is almost-sure. It is of interest that the embedded Galton-Watson process of successive generations need not have a finite mean for the conditions of the above theorems to hold. Similar results are obtained for the age-distribution as well.

Keywords

AGE-DEPENDENT BRANCHING PROCESSESALMOST-SURE CONVERGENCERATES OF RENEWAL CONVERGENCEAGE DISTRIBUTIONS
Type
Research Papers
Information
Journal of Applied Probability , Volume 11 , Issue 4 , December 1974 , pp. 678 - 686
Copyright
Copyright © Applied Probability Trust 1974 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Athreya, K. B. and Ney, P. E. (1972) Branching Processes. Springer-Verlag, Berlin.Google Scholar
Crump, K. S. and Mode, C. J. (1968) A general age-dependent branching process I. J. Math. Anal. Appl. 24, 494–508.Google Scholar
Crump, K. S. and Mode, C. J. (1969) A general age-dependent branching process II. J. Math. Anal. Appl. 25, 8–17.Google Scholar
Doney, R. A. (1972a) A limit theorem for a class of supercritical branching processes. J. Appl. Prob. 9, 707–724.Google Scholar
Doney, R. A. (1972b) Age-dependent birth-and-death processes. Z. Wahrscheinlichkeitsth. 22, 69–90.Google Scholar
Durham, S. D. (1971) Limit theorems for a general critical branching process. J. Appl. Prob. 8, 1–16.Google Scholar
Feller, W. (1966) An Introduction to Probability Theory and its Applications. John Wiley, New York.Google Scholar
Ganuza, E. (1972) Limit laws for supercritical one-dimensional age-dependent branching processes with age-dependent transition probabilities. Ph. D. Dissertation, University of Colorado.Google Scholar
Ganuza, E. (1973) On the supercritical general branching process. To appear.Google Scholar
Harris, T. E. (1963) The Theory of Branching Processes. Springer-Verlag, Berlin.Google Scholar
Jagers, P. (1968) Renewal theory and the almost-sure convergence of branching processes. Ark. Mat. 7, 495–504.Google Scholar
Jagers, P. (1969) A general stochastic model for population development Skand. Aktuartidskr. 52, 84–103.Google Scholar
Mode, C. J. (1971) Multitype Branching Processes: Theory and Applications. American Elsevier, New York.Google Scholar