Hostname: page-component-76fb5796d-skm99 Total loading time: 0 Render date: 2024-04-26T08:01:10.951Z Has data issue: false hasContentIssue false
  • English
  • Français

Large deviations of Poisson Telecom processes

Part of: Distribution theory - Probability Stochastic processes Limit theorems

Published online by Cambridge University Press:  12 October 2022

Mikhail Lifshits Open the ORCID record for Mikhail Lifshits [Opens in a new window]  and
Sergei Nikitin
Mikhail Lifshits*
Affiliation:
St. Petersburg State University
Sergei Nikitin*
Affiliation:
St. Petersburg State University
*
*Postal address: St. Petersburg State University, University Emb. 7/9, 199034, St. Petersburg, Russia.
*Postal address: St. Petersburg State University, University Emb. 7/9, 199034, St. Petersburg, Russia.
Get access Rights & Permissions [Opens in a new window]

Abstract

We study large-deviation probabilities of Telecom processes appearing as limits in a critical regime of the infinite-source Poisson model elaborated by I. Kaj and M. Taqqu. We examine three different regimes of large deviations (LD) depending on the deviation level. A Telecom process 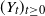$(Y_t)_{t \ge 0}$ scales as 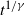$t^{1/\gamma}$ , where t denotes time and 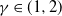$\gamma\in(1,2)$ is the key parameter of Y. 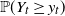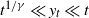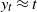We must distinguish moderate LD ${\mathbb P}(Y_t\ge y_t)$ with $t^{1/\gamma} \ll y_t \ll t$ , intermediate LD with $ y_t \approx t$ , and ultralarge LD with 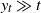$ y_t \gg t$ . The results we obtain essentially depend on another parameter of Y, namely the resource distribution. We solve completely the cases of moderate and intermediate LD (the latter being the most technical one), whereas the ultralarge deviation asymptotics is found for the case of regularly varying distribution tails. In all the cases considered, the large-deviation level is essentially reached by the minimal necessary number of ‘service processes’.

Keywords

Large-deviation probabilitiesTelecom processPoisson random measureteletrafficworkload

MSC classification

Primary: 60F10: Large deviations
Secondary: 60F05: Central limit and other weak theorems 60G57: Random measures 60E07: Infinitely divisible distributions; stable distributions
Type
Original Article
Information
Journal of Applied Probability , Volume 60 , Issue 1 , March 2023 , pp. 267 - 283
Check for updates
Copyright
© The Author(s), 2022. Published by Cambridge University Press on behalf of Applied Probability Trust

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Cohen, S. and Taqqu, M. (2004). Small and large scale behavior of the Poissonized Telecom process, Methodology Comput. Appl. Prob. 6, 363–379.CrossRefGoogle Scholar
Dembo, A. and Zeitouni, O. (2010). Large Deviations Techniques and Applications, Springer, New York.CrossRefGoogle Scholar
Gaigalas, R. and Kaj, I. (2003). Convergence of scaled renewal processes and a packet arrival model. Bernoulli 9, 671–703.CrossRefGoogle Scholar
Gaigalas, R. (2006). A Poisson bridge between fractional Brownian motion and stable Lévy motion. Stoch. Process Appl. 116, 447–462.CrossRefGoogle Scholar
Kaj, I. (2002). Stochastic Modeling in Broadband Communications Systems, SIAM, Philadelphia.CrossRefGoogle Scholar
Kaj, I. (2005). Limiting fractal random processes in heavy-tailed systems. In Fractals in Engineering: New Trends in Theory and Applications, eds J. Levy-Vehel and E. Lutton, Springer, London, pp. 199–218.CrossRefGoogle Scholar
Kaj, I. (2006). Aspects of wireless network modeling based on Poisson point processes, Fields Institute Workshop on Applied Probability, Carleton University, Ottawa.Google Scholar
Kaj, I., Leskelä, L., Norros, I., and Schmidt, V. (2007). Scaling limits for random fields with long-range dependence, Ann. Prob. 35, 528–550.CrossRefGoogle Scholar
Kaj, I. and Taqqu, M. S. (2008). Convergence to fractional Brownian motion and to the Telecom process: The integral representation approach. In In and Out of Equilibrium, Vol. II., Progress in Prob. 60, Birkhäuser, Basel, pp. 383–427.10.1007/978-3-7643-8786-0_19CrossRefGoogle Scholar
Kurtz, T. G. (1996). Limit theorems for workload input models. In Stochastic Networks: Theory and Applications, eds F. P. Kelly, S. Zachary, and I. Ziedins, Clarendon Press, Oxford, pp. 119–140.Google Scholar
Lifshits, M. (2014). Random Processes by Example, World Scientific, Singapore.CrossRefGoogle Scholar
Pipiras, V. and Taqqu, M. S. (2000). The limit of a renewal–reward process with heavy-tailed rewards is not a linear fractional stable motion. Bernoulli 6, 607–614.10.2307/3318508CrossRefGoogle Scholar
Rosenkrantz, W. A. and Horowitz, J. (2002). The infinite source model for internet traffic: Statistical analysis and limit theorems, Methods Appl. Anal. 9, 445–462.Google Scholar
Taqqu, M. S. (2002). The modeling of Ethernet data and of signals that are heavy-tailed with infinite variance, Scand. J. Statist. 29, 273–295.CrossRefGoogle Scholar