Hostname: page-component-76fb5796d-r6qrq Total loading time: 0 Render date: 2024-04-26T03:02:08.567Z Has data issue: false hasContentIssue false
  • English
  • Français

Asymptotic persistence time formulae for multitype birth–death processes

Part of: Markov processes

Published online by Cambridge University Press:  21 March 2023

Frank G Ball Open the ORCID record for Frank G Ball [Opens in a new window]  and
Damian Clancy Open the ORCID record for Damian Clancy [Opens in a new window]
Frank G Ball*
Affiliation:
University of Nottingham
Damian Clancy*
Affiliation:
Heriot-Watt University
*
*Postal address: School of Mathematical Sciences, University of Nottingham, Nottingham, NG7 2RD, UK. Email address: frank.ball@nottingham.ac.uk
**Postal address: Department of Actuarial Mathematics and Statistics, Maxwell Institute for Mathematical Sciences, Heriot-Watt University, Edinburgh, EH14 4AS, UK. Email address: d.clancy@hw.ac.uk
Get access Rights & Permissions [Opens in a new window]

Abstract

We consider a class of processes describing a population consisting of k types of individuals. The process is almost surely absorbed at the origin within finite time, and we study the expected time taken for such extinction to occur. We derive simple and precise asymptotic estimates for this expected persistence time, starting either from a single individual or from a quasi-equilibrium state, in the limit as a system size parameter N tends to infinity. Our process need not be a Markov process on 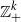$ {\mathbb Z}_+^k$; we allow the possibility that individuals’ lifetimes may follow more general distributions than the exponential distribution.

Keywords

Large deviationspopulation processesstochastic epidemic models

MSC classification

Primary: 60J27: Continuous-time Markov processes on discrete state spaces
Secondary: 92D30: Epidemiology 92D40: Ecology
Type
Original Article
Information
Journal of Applied Probability , Volume 60 , Issue 3 , September 2023 , pp. 895 - 920
Check for updates
Copyright
© The Author(s), 2023. Published by Cambridge University Press on behalf of Applied Probability Trust

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Assaf, M. and Meerson, B. (2010). Extinction of metastable stochastic populations. Phys. Rev. E 81, article no. 021116.CrossRefGoogle ScholarPubMed
Assaf, M. and Meerson, B. (2017). WKB theory of large deviations in stochastic populations. J. Phys. A 50, article no. 263001.10.1088/1751-8121/aa669aCrossRefGoogle Scholar
Ball, F. G. (1983). The threshold behaviour of epidemic models. J. Appl. Prob. 20, 227–241.10.2307/3213797CrossRefGoogle Scholar
Ball, F. G., Britton, T. and Neal, P. (2014). On expected durations of birth–death processes, with applications to branching processes and SIS epidemics. Preprint. Available at https://arxiv.org/abs/1408.0641.Google Scholar
Ball, F. G., Britton, T. and Neal, P. (2016). On expected durations of birth–death processes, with applications to branching processes and SIS epidemics. J. Appl. Prob. 53, 203–215.10.1017/jpr.2015.19CrossRefGoogle Scholar
Ball, F. G. and O’Neill, P. D. (1994). Strong convergence of stochastic epidemics. Adv. Appl. Prob. 26, 629–655.10.2307/1427812CrossRefGoogle Scholar
Chazottes, J. B., Collet, P. and Méléard, S. (2019). On time scales and quasi-stationary distributions for multitype birth-and-death processes. Ann. Inst. H. Poincaré Prob. Statist. 55, 2249–2294.10.1214/18-AIHP948CrossRefGoogle Scholar
Clancy, D. (2018). Persistence time of SIS infections in heterogeneous populations and networks. J. Math. Biol. 77, 545–570.CrossRefGoogle ScholarPubMed
Clancy, D. (2018). Precise estimates of persistence time for SIS infections in heterogeneous populations. Bull. Math. Biol. 80, 2871–2896.10.1007/s11538-018-0491-6CrossRefGoogle ScholarPubMed
Clancy, D. and Pollett, P. K. (2003). A note on quasi-stationary distributions of birth–death processes and the SIS logistic epidemic. J. Appl. Prob. 40, 821–825.10.1239/jap/1059060909CrossRefGoogle Scholar
Davis, M. H. A. (1993). Markov Models and Optimization. Chapman and Hall, London.10.1007/978-1-4899-4483-2CrossRefGoogle Scholar
Diekmann, O., Heesterbeek, J. A. P. and Roberts, M. G. (2010). The construction of next-generation matrices for compartmental epidemic models. J. R. Soc. Interface 7, 873–885.10.1098/rsif.2009.0386CrossRefGoogle ScholarPubMed
Ethier, S. N. and Kurtz, T. G. (2005). Markov Processes: Characterization and Convergence. John Wiley, New York.Google Scholar
Hernández-Suárez, C. M. and Castillo-Chavez, C. (1999). A basic result on the integral for birth–death Markov processes. Math. Biosci. 161, 95–104.10.1016/S0025-5564(99)00034-6CrossRefGoogle ScholarPubMed
Keilson, J. and Ramaswamy, R. (1984). Convergence of quasistationary distributions in birth–death processes. Stoch. Process. Appl. 18, 301–312.10.1016/0304-4149(84)90302-8CrossRefGoogle Scholar
Kelly, F. P. (2011). Reversibility and Stochastic Networks. Cambridge University Press.Google Scholar
Kryscio, R. J. and Lefèvre, C. (1989). On the extinction of the S-I-S stochastic logistic epidemic. J. Appl. Prob. 26, 685–694.10.2307/3214374CrossRefGoogle Scholar
Laub, A. J. (2005). Matrix Analysis for Scientists and Engineers. Society for Industrial and Applied Mathematics, Philadelphia.Google Scholar
Mode, C. J. (1971). Multitype Branching Processes: Theory and Applications. Elsevier, New York.Google Scholar
Ovaskainen, O. and Meerson, B. (2010). Stochastic models of population extinction. Trends Ecol. Evolution 25, 643–652.10.1016/j.tree.2010.07.009CrossRefGoogle ScholarPubMed
Sellke, T. (1983). On the asymptotic distribution of the size of a stochastic epidemic. J. Appl. Prob. 20, 390–394.CrossRefGoogle Scholar
Van den Driessche, P. and Watmough, J. (2002). Reproduction numbers and sub-threshold endemic equilibria for compartmental models of disease transmission. Math. Biosci. 180, 29–48.10.1016/S0025-5564(02)00108-6CrossRefGoogle ScholarPubMed
Zachary, S. (2007). A note on insensitivity in stochastic networks. J. Appl. Prob. 44, 238–248.CrossRefGoogle Scholar