Transform inversions, in which density and survival functions are computed from their associated moment generating function 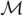$\mathcal{M}$, have largely been based on methods which use values of 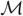$\mathcal{M}$ in its convergence region. Prominent among such methods are saddlepoint approximations and Fourier-series inversion methods, including the fast Fourier transform. In this paper we propose inversion methods which make use of values for 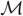$\mathcal{M}$ which lie outside of its convergence region and in its analytic continuation. We focus on the simplest and perhaps richest setting for applications in which 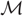$\mathcal{M}$ is either a meromorphic function in its analytic continuation, so that all of its singularities are poles, or else the singularities are isolated essential. Asymptotic expansions of finite- and infinite-orders are developed for density and survival functions using the poles of 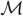$\mathcal{M}$ in its analytic continuation. For finite-order expansions, the expansion error is a contour integral in the analytic continuation, which we approximate using the saddlepoint method based on following the path of steepest descent. Such saddlepoint error approximations accurately determine expansion errors and, thus, provide the means for determining the order of the expansion needed to achieve some preset accuracy. They also provide an additive correction term which increases accuracy of the expansion. Further accuracy is achieved by computing the expansion errors numerically using a contour path which ultimately tracks the steepest descent direction. Important applications include Wilks’ likelihood ratio test in MANOVA, compound distributions, and the Sparre Andersen and Cramér–Lundberg ruin models.