Hostname: page-component-77c89778f8-5wvtr Total loading time: 0 Render date: 2024-07-24T03:40:24.525Z Has data issue: false hasContentIssue false
  • English
  • Français

An exponential change of measure for the Feller diffusion and some implications for superprocesses

Part of: Markov processes Stochastic processes Stochastic analysis

Published online by Cambridge University Press:  14 July 2016

Robert J. Adler  and
Srikanth K. Iyer
Robert J. Adler*
Affiliation:
Technion, Israel Institute of Technology
Srikanth K. Iyer*
Affiliation:
Indian Institute of Technology
*
∗Postal address: Faculty of Industrial Engineering and Management, Technion, Haifa, 32000 Israel. Email address: robert@ieadler.technion.ac.il
∗∗Postal address: Department of Mathematics, Indian Institute of Technology, Kanpur, UP 27516, India. Email address: skiyer@iitk.ernet.in
Get access Rights & Permissions [Opens in a new window]

Abstract

Let Xt be a Feller (branching) diffusion with drift αx. We consider new processes, the probability measures of which are obtained from that of X via changes of measure involving suitably normalized exponential functions of 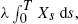with λ > 0. The new processes can be thought of as ‘self-reinforcing’ versions of the old.

Depending on the values of α, T and λ, the process under the new measure is shown to exhibit explosion in finite time. We also obtain a number of other results related to the new processes.

Since the Feller diffusion is also the total mass process of a superprocess, we relate the finite-time explosion property to the behaviour of superprocesses with local self-interaction, and raise some interesting questions for these.

Keywords

Feller diffusionchange of measureoccupation measureself-reinforcementself-interactionsuperprocess

MSC classification

Primary: 60J55: Local time and additive functionals 60G57: Random measures
Secondary: 60G30: Continuity and singularity of induced measures 60H15: Stochastic partial differential equations
Type
Short Communications
Information
Journal of Applied Probability , Volume 37 , Issue 1 , March 2000 , pp. 236 - 245
Copyright
Copyright © 2000 by The Applied Probability Trust 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

Research supported in part by US–Israel Binational Science Foundation, Israel Science Foundation, and National Science Foundation (RJA).

Research supported in part by ONR Grant No. N00014-94-1-0191 (SKI).

References

Adler, R. J., and Ivanitskaya, L. (1996). A superprocess with a disappearing self-interaction. J. Theor. Prob. 9, 245–261.Google Scholar
Adler, R. J., and Iyer, S. K. (1998). On the exponential change of measure for the superprocess. Submitted. Available at http://iew3.technion.ac.il:8080/Home/Users/Adler.phtml.Google Scholar
Adler, R. J., and Tribe, R. (1998). Uniqueness for a historical SDE with a singular interaction. J. Theor. Prob. 11, 515–533.Google Scholar
Dawson, D. (1978). Geostochastic calculus. Canad. J. Statist. 6, 143–168.CrossRefGoogle Scholar
Dawson, D. (1993). Measure valued Markov processes. In Ecole dEté de Probabilités de Saint-Flour, XXI (Lecture Notes in Math. 1541). Springer, New York, pp. 1–260.Google Scholar
Dawson, D., and Fleischmann, K. (1994). A super-Brownian motion with a single point catalyst. Stoch. Proc. Appl. 49, 3–40.Google Scholar
Dawson, D., and Perkins, E. A. (1991). Historical processes. Amer. Math. Soc. Mem. 93, 1–179.Google Scholar
Iscoe, I. (1986). A weighted occupation time for a class of measure valued branching processes. Z. Wahrscheinlichkeitsth. 71, 85–116.CrossRefGoogle Scholar
Iscoe, I. (1986). Ergodic theory and a local occupation time for measure valued critical branching Brownian motion. Stochastics 18, 197–243.Google Scholar
Perkins, E. (1992). Measure valued branching diffusions with spatial interactions. Prob. Theory Rel. Fields 94, 189–245.Google Scholar
Pitman, J., and Yor, M. (1982). A decomposition of Bessel bridges. Z. Wahrscheinlichkeitsth. 59, 425–457.Google Scholar
Revuz, D., and Yor, M. (1994). Continuous Martingales and Brownian Motion, 2nd edn. Springer, Berlin.Google Scholar
Varadhan, S. R. S. (1969). Appendix to Symanzik, K. In Local Quantum Theory, ed. R. Jost. Academic Press, New York, pp. 219–226.Google Scholar
Westwater, J. (1980) On Edwards' model for polymer chains Commun. Math. Phys. 72, 131–174.Google Scholar
Westwater, J. (1982). On Edwards' model for polymer chains III, Borel summability. Commun. Math. Phys. 84, 459–470.Google Scholar