1. Introduction
The Agricultural Act of 2014 offers new crop insurance options to farmers producing all major U.S. commodity crops. Shallow loss (SL) insurance offered under the program could act as a substitute for commodity programs, especially in cotton.Footnote 1, Footnote 2 A new Yield Exclusion (YE) provision also makes substantial potential changes to the existing individual-coverage insurance products in terms of effective coverage levels. Further, farmers can now separate irrigated and nonirrigated acres in enterprise unit coverage. The risk profile of irrigated and nonirrigated acres is different because of higher variance in productivity, which depends on weather/soil moisture conditions; this is more evident in cotton.
In these new policies, farmers can change their decision every year. Previous studies have suggested that there may be low participation in the early stages of a program, especially for a program in which farmers can change their decision every year (Coble et al., Reference Coble, Knight, Pope and Williams1996; Zering, McCorkle, and Moore, Reference Zering, McCorkle and Moore1987). Farmers adding a Stacked Income Protection Plan (STAX) policy were only 14% in 2015. With respect to acreage, 29% of cotton acreage added STAX. In Texas, only 20% of total insured acres were in STAX. Only 0.1% of total cotton acres were insured with Supplemental Coverage Option (SCO) in 2015. Regarding YE, out of 89% of total eligible insured acres, only 23% selected YE for the 2015 crop (U.S. Department of Agriculture, Risk Management Agency [USDA-RMA], 2016).
Over the years, U.S. farm programs have been moving away from commodity programs to insurance programs. In addition to other factors, SL coverage for cotton was intended to comply with a 2009 World Trade Organization (WTO) ruling. In cotton, participation in SL program was significantly lower than expected, as the participation was expected to substitute for commodity program participation.Footnote 3 Analyzing the net benefit of the SL program and the YE provision could give insight into understanding the lower participation and provide direction for future policy making.Footnote 4
We are not aware of previous studies examining optimal insurance decisions based on land productivity and farmers’ evaluation of county yield and its correlation to farm yield. The understanding of farmers’ knowledge is necessary to predict the success of implementing new policies, especially in SL insurance programs. Further, to our knowledge, there are also no published studies analyzing YE provisions, which have larger cost-benefit implications for farmers. Therefore, this study addresses the broader lack of knowledge about cotton farmers regarding implications of their insurance decisions in the current policy scenario and also addresses some of the potential impacts of SL insurance and the YE provision.
These new policies have the potential to affect farmers’ decisions on risk management strategies, and it is important to understand those decisions for future farm bill implementation. Compared with other crops, cotton has only a limited safety net available and has higher exposure to new policies. With availability of limited resources, analyzing the cotton insurance choices can give a broader assessment of the implications of experience under the Agricultural Act of 2014 for the development of future policies. The primary previous study examining these new options addressed only irrigated cotton farms in the northern High Plains of Texas (Bulut and Collins, Reference Bulut and Collins2013). Two earlier studies (Dismukes et al., Reference Dismukes, Coble, Miller and O'Donoghue2013; Paulson, Woodard, and Babcock, Reference Paulson, Woodard and Babcock2013) provide broad national estimates but no estimates specific to the Texas High Plains region, which is a major cotton-producing region (U.S. Department of Agriculture, National Agricultural Statistics Services [USDA-NASS], 2009, 2015). Other authors have studied the implications of SL insurance for other major crops (Cooper, Hungerford, and O'Donoghue, Reference Cooper, Hungerford and O'Donoghue2015; Zulauf and Schnitkey, Reference Zulauf and Schnitkey2015). This study addresses the effect of choosing SL insurance along with YE, which was not addressed previously. Again, understanding the cost-benefit structure of these policies could give direction for the development of upcoming farm bills.
The objective of this study is to assess the benefits of the new crop insurance products and provisions for nonirrigated cotton farmers in the Texas southern High Plains. We use simulation techniques to analyze farmer welfare benefits from alternative combinations of underlying yield or revenue insurance coverages, two new SL products (STAX and SCO), and YE.Footnote 5 This is the first analysis conducted using farmers’ assessments of farm and county yield distributions and farm-county yield correlations, which are critical underlying elements when choosing an area-type insurance product represented by SL products because their benefits are triggered by a county yield, not farm yield/revenue.Footnote 6 This study evaluates the benefits of different insurance policies in an enterprise unit insurance product as farmers can separate irrigated and nonirrigated acres in the new program.Footnote 7
The differences between STAX and SCO are shown in Table 1. As the two different SL insurance products have different benefit structures, the understanding of farm-level productivity may help a farmer to decide which one is the optimal SL insurance policy. To address this possibility, we assess the optimal insurance choice between a high- (higher farm yield than county) and low-productivity farm (lower farm yield than county). Further, the YE policy increases actual production history (APH) yield with an increase in the premium, which may lead farmers to change their coverage level choices compared with previous years. This option is also modeled.
Table 1. Difference between Stacked Income Protection Plan (STAX) and Supplemental Coverage Option (SCO)

We should note at the outset that moral hazard effects are not considered in our analysis. The potential for moral hazard in crop insurance has been recognized at least since the 1980s (Coble and Knight, Reference Coble, Knight, Just and Pope2002; Coble et al., Reference Coble, Knight, Pope and Williams1997; Nelson and Loehman, Reference Nelson and Loehman1987; Skees and Reed, Reference Skees and Reed1986; Smith and Goodwin, Reference Smith and Goodwin1996). The reason we do not consider moral hazard responses affecting input use and net revenue is because of the additional demands it would have placed on cooperating producers who were already being asked to provide extensive data through a careful assessment and review process. This is a weakness of the study, which needs to be addressed in future research.
2. Conceptual Framework
The farmer's choice of insurance depends on protecting yield, price/revenue, risk aversion characteristics, and policy subsidy effects on insurance premiums. Risk aversion directly relates to willingness to pay for risk shifting, and premium subsidies reduce the cost of that insurance at each coverage level. The combination of these factors leads to optimal product choice.
The choice of SL insurance depends on both farm yield and county yield. The SCO yield guarantee is based on the farm yield, and STAX is based on county yield, but both products trigger losses based on county yield. One factor of SL insurance choice is yield correlation between the farm and county. In other words, if the farm yield distribution is similar to the county yield distribution, SL products act simply as a more highly subsidized version of individual farm insurance.Footnote 8 The farm yield distribution does not affect the yield guarantee in STAX; however, in the case of SCO, low- and high-productivity farms have different yield guarantees based on farm yield. The high-productivity farm has a higher yield guarantee compared with the county yield. The low-productivity farm has a lower yield guarantee compared with county yield. This difference in yield guarantee and subsidy rate determines the optimal policy and benefits from the SL insurance policy. The addition of YE changes the yield guarantee on SCO, but not on STAX.
Farmers are assumed to seek to maximize their expected utility of ending wealth under uncertainty. The expected utility evaluation of insurance choices as risk management tools is conditioned on farmers’ risk preferences and subjective evaluations of the risk they confront. This analysis assumes the farmers are risk averse and have risk preferences consistent with a constant relative risk aversion (CRRA) function. The CRRA function implies the decision of the individual does not vary in terms of budget share, or income elasticities are equal to 1. Mathematically, the utility function assuming CRRA is the following:
 $$\begin{equation}
{U_{n\alpha i}} = \frac{{{W_{n\alpha i}}^{1 - r}}}{{1 - r}}.
\end{equation}$$
$$\begin{equation}
{U_{n\alpha i}} = \frac{{{W_{n\alpha i}}^{1 - r}}}{{1 - r}}.
\end{equation}$$
In equation (1), W is the net stochastic ending wealth for choosing specific insurance (α) with coverage level i, n is the number of simulations, and r is the coefficient of relative risk aversion (Arrow-Pratt coefficient). The ending wealth (equation 2) consists of initial farmer wealth, farmer insurance premiums (net of subsidy), actual revenue, and indemnities.
 $$\begin{eqnarray}
{W_{n\alpha i}} & = & {\rm{Initial\ Wealth}} + {\rm{Actual\ Revenu}}{{\rm{e}}_n} - {\rm{Production\ Cost}} \nonumber\\
&&+\, {\rm{\ \ Indemnit}}{{\rm{y}}_{n\alpha i}}{\rm{\ }} - {\rm{\ Net\ Insurance\ Premiu}}{{\rm{m}}_{\alpha i}}.
\end{eqnarray}$$
$$\begin{eqnarray}
{W_{n\alpha i}} & = & {\rm{Initial\ Wealth}} + {\rm{Actual\ Revenu}}{{\rm{e}}_n} - {\rm{Production\ Cost}} \nonumber\\
&&+\, {\rm{\ \ Indemnit}}{{\rm{y}}_{n\alpha i}}{\rm{\ }} - {\rm{\ Net\ Insurance\ Premiu}}{{\rm{m}}_{\alpha i}}.
\end{eqnarray}$$
The initial wealth and production cost are assumed constant for all insurance policies. The net insurance premium is the farmer paid insurance premium after subsidy, which is different for each insurance policy and coverage level. The actual revenue is the product of n simulations of harvest price and yield.Footnote 9 The different risk management choices were examined with the certainty equivalent (CE) of the net stochastic ending wealth (W nαi). This analysis used a model that is consistent with Vedenov and Power (Reference Vedenov and Power2008), Power, Vedenov, and Hong (Reference Power, Vedenov and Hong2009), Wang et al. (Reference Wang, Barnett, Coble and Harri2012), Dismukes et al. (Reference Dismukes, Coble, Miller and O'Donoghue2013), and Bulut and Collins (Reference Bulut and Collins2014) using a CRRA utility function. The expected utility is as follows:
 $$\begin{equation}
E\left[ {{U_{n\alpha i}}} \right] = \ \mathop \sum \limits_1^n {\omega _{n\alpha i\ }}\frac{{W_{n\alpha i}^{1 - r}}}{{1 - r}}.
\end{equation}$$
$$\begin{equation}
E\left[ {{U_{n\alpha i}}} \right] = \ \mathop \sum \limits_1^n {\omega _{n\alpha i\ }}\frac{{W_{n\alpha i}^{1 - r}}}{{1 - r}}.
\end{equation}$$
Here, E represents the expectation operator, and ωnαi is the probability of the respective ending wealth. The r was set equal to 2 to represent the moderate level of risk aversion level,Footnote 10 which has been used in several previous studies (Bulut and Collins, Reference Bulut and Collins2014; Dismukes et al., Reference Dismukes, Coble, Miller and O'Donoghue2013; Power, Vedenov, and Hong, Reference Power, Vedenov and Hong2009; Vedenov and Power, Reference Vedenov and Power2008). We calculated the CE from expected utility as shown in equation (4). The CE is a measure of expected benefits calculated considering all the costs and subsidies associated with agricultural production, insurance cost, and farmer's initial wealth. The benefits are higher for the insurance choice having the highest CE. The results are expressed in net benefit per acre for easier interpretation. It is calculated with the difference of two CEs, which is shown in equation (5) (CE of a specific insurance with a coverage level, CEαi, and CE of no insurance, CE0). Further, this difference is divided by net acresFootnote 11 to express the results in dollars per acre unit as shown in equation (5).
3. Data
The data for this study were collected through use of a focus group of farmers used to develop a representative nonirrigated cotton farm for Lynn County, Texas, during summer 2014. The Texas southern High Plains is the largest contiguous cotton-growing region of the United States (USDA-NASS, 2009, 2015). Lynn County was chosen, as cotton was the major planted crop of the county with most of it being nonirrigated cotton. On average, for the last 10 years in Lynn County, 90% of the planted acres have been cotton, and 75% of the cotton acres were nonirrigated cotton (USDA-NASS, 2014). This condition minimized the effect of revenue and insurance choices from other crops. The group of farmers participating in the process of developing the representative farm was not a random sample, but rather a group of typical farmers representing their county.Footnote 12 The participants (4 farmers from Lynn County) developed a consensus about typical farming operations in the county to create the representative 2,500-acre nonirrigated cotton farm.Footnote 13
The information obtained from the focus group included the financial and physical structure of initial wealth, operating costs, farm and county yield distribution characteristics, and correlations between farm and county yields (see the online supplementary material for the questionnaire and focus group process in detail). We calculated the beginning net worth and the final net worth from the information collected from the focus group to estimate the financial status of the representative farm. In this process, we constructed a balance sheet, budget, and income statement (see Appendices I, II, and III in the online supplementary material). The premium cost for each insurance type is calculated using the RMA cost estimator to get information about base premium rate, a county reference yield for the respective insurance product, and a subsidy rate for the different coverage levels (USDA-RMA, 2014b; Appendix IV in the online supplementary material). While deciding on an insurance policy, farmers update their county yield information through insurance agents.Footnote 14 Indemnity functions for each policy are shown in Appendix V in the online supplementary material (USDA-RMA, 2014a).
Each insurance policy has different risk protection structures. The different crop insurance policy choices include an underlying policy only (Common Crop Insurance Provisions [CCIP]), an underlying policy with SCO endorsement, STAX Revenue Protection (STAX-RP) only, STAX Revenue Protection with Harvest Price Exclusion (STAX-RPHPE) only, an underlying CCIP with STAX-RP, and an underlying CCIP with STAX-RPHPE. All possible coverage levels for these different policies were analyzed. This study also conducted a sensitivity analysis to assess the impact of APH YE. For both a low- and a high-productivity nonirrigated cotton farm, a 20% increase in APH was added to approximate the typical effects of a YE for Lynn County.Footnote 15
4. Simulation Process
We use a project evaluation and review technique type method of three-point estimation to estimate the parameters required for simulating beta yield distributions for high-productivity and low-productivity nonirrigated cotton farms for Lynn County (Davidson and Cooper, Reference Davidson and Cooper1976). This method was used to compute the sample mean and sample standard deviation of subjective yield distributions based on the elicited 10th fractile, 90th fractile, and mode of the distribution collected from the cotton farmers.
We assume a beta distribution for farm and county yields as in previous studies (Babcock and Hennessy, Reference Babcock and Hennessy1996; Borges and Thurman, Reference Borges and Thurman1994; Coble et al., Reference Coble, Knight, Pope and Williams1996). The parameters required to simulate the beta distribution are mean, variance, and lower and upper bounds. The upper and lower bounds for the beta distribution were calculated using lower bound (a) = max (µ − 4s, 0) and upper bound (c) = µ + 2s, where, µ is the sample mean and s is the sample standard deviation (Babcock, Hart, and Hayes, Reference Babcock, Hart and Hayes2002). When the lower and upper bounds are not 0 and 1, respectively, the sample mean and sample variance should be modified as follows (U.S. Department of Commerce, National Institute of Standards and Technology, 2012):
 $$\begin{equation}
{\rm{Modified\ Mean\ }}\left( {\bar{x}} \right) = {\rm{\ }}\frac{{{\rm{sample\ mean\ }} - {\rm{\ lower\ bound}}}}{{{\rm{upper\ bound\ }} - {\rm{\ lower\ bound}}}},
\end{equation}$$ \\
$$\begin{equation}
{\rm{Modified\ Mean\ }}\left( {\bar{x}} \right) = {\rm{\ }}\frac{{{\rm{sample\ mean\ }} - {\rm{\ lower\ bound}}}}{{{\rm{upper\ bound\ }} - {\rm{\ lower\ bound}}}},
\end{equation}$$ \\
 $$\begin{equation}
{\rm{Modified\ Variance}}\left( {{{\bar{s}}^2}} \right) = {\rm{\ }}\frac{{{\rm{sample\ variance}}}}{{{{\left( {{\rm{upper\ bound\ }} - {\rm{\ lower\ bound}}} \right)}^2}}}.
\end{equation}$$
$$\begin{equation}
{\rm{Modified\ Variance}}\left( {{{\bar{s}}^2}} \right) = {\rm{\ }}\frac{{{\rm{sample\ variance}}}}{{{{\left( {{\rm{upper\ bound\ }} - {\rm{\ lower\ bound}}} \right)}^2}}}.
\end{equation}$$
The modified mean and standard deviation were used to calculate the alpha and beta parameters of beta distribution as in equation (11) and (12):
 $$\begin{equation}
{\rm{alpha}} = \ \overline {x\ } \left( {\frac{{\ \bar{x}\ \left( {1\ - \ \bar{x}} \right)\ }}{{{{\bar{s}}^2}}}\ - 1} \right),
\end{equation}$$
$$\begin{equation}
{\rm{alpha}} = \ \overline {x\ } \left( {\frac{{\ \bar{x}\ \left( {1\ - \ \bar{x}} \right)\ }}{{{{\bar{s}}^2}}}\ - 1} \right),
\end{equation}$$
 $$\begin{equation}
{\rm{beta}} = \ \left( {\frac{{\ {\rm{alpha}}\ \left( {1\ - \ \bar{x}\ } \right)}}{{\bar{x}}}} \right).
\end{equation}$$
$$\begin{equation}
{\rm{beta}} = \ \left( {\frac{{\ {\rm{alpha}}\ \left( {1\ - \ \bar{x}\ } \right)}}{{\bar{x}}}} \right).
\end{equation}$$
The harvest price is assumed to be log normally distributed as assumed by USDA-RMA (2015b). This study uses the strength-of-relationship method as one of the dependence-assessment methods to elicit correlations among yields and price (Clemen, Fischer, and Winkler, Reference Clemen, Fischer and Winkler2000). In this method, farmers were asked to choose the relationship between there farm yield and county yield subjectively to calculate the yield correlation as in equation (13).
 $$\begin{equation}
{r_s} = \ \left( {\frac{{\ s\ - \ 4}}{3}} \right)
\end{equation}$$
$$\begin{equation}
{r_s} = \ \left( {\frac{{\ s\ - \ 4}}{3}} \right)
\end{equation}$$
A correlated probability matrix of 50,000 observations (n) of yields and prices was simulated using the Phoon, Quek, and Huang multivariate simulation method (Anderson, Harri, and Coble, Reference Anderson, Harri and Coble2009; Phoon, Quek, and Huang, Reference Phoon, Quek and Huang2004). The inverse transformation method was used to simulate the yield distribution. Simulated yields and price were used to evaluate all the policies stated previously for land of low- and high-productivity farm yield. The insurance premium, indemnity, expected utility, and CE were calculated to identify the optimal policy choice.
5. Description of Data
The Lynn County nonirrigated cotton representative farm consists of 2,500 acres, of which 667 acres is owned and 1,833 acres is share leased. Both low- and high-productivity farms are assumed to be the same size to make our results comparable. The yield of a low-productivity farm has a mean of 302 pounds per acre with standard deviation of 146 pounds. The yield of a high-productivity farm has a mean of 494 pounds per acre with standard deviation of 187 pounds. The RMA-expected county yield is 282 pounds per acre. The county yield expectation of the RMA is lower than that obtained from the farmers. The expected price of cotton is $0.64 per pound, and standard deviation is $0.114 per pound. Based on information provided by the farmers, the correlation between farm and county yield is 0.67, which is moderate. The rank correlation matrix is presented in the Table 2. Even though the correlation was generated using farmers’ information, the sensitivity analysis of the correlation between farm and county yield was conducted. The sensitivity analysis was conducted assuming the correlation between farm and county yield as low, or very low, or high or very high. Other information used in the simulation and construction of the Lynn County nonirrigated cotton farm is given in Appendix IV in the online supplementary material.
Table 2. Rank Correlation Matrix

6. Simulation Results and Discussion
When the farmers did not purchase insurance, the estimated net revenues per acre are $462.08 and $350.34 for the high- and low-productivity farms, respectively.Footnote 16 The benefits from simulating different insurance policies are compared with the no insurance net revenue dollars per acre.Footnote 17 Farmers can choose any one of the following possible combinations of different policies,Footnote 18 which are CCIP product only, CCIP in combination with SL product, CCIP with YE, or CCIP with YE and SL product.
The CCIP products are traditional products, and farmers have a general understanding of these products. Among the CCIP products only, the optimal coverage level is at 75% for all CCIP products, which are Yield Protection, RP, and RPHPE. Among the CCIP products, RP has highest dollar benefit of $28.49 per acre more than no insurance at the 75% coverage level (Tables 3 and 4). The results for STAX and SCO are discussed focusing on RMA-expected county yield.Footnote 19 The RMA-expected county yield is the yield used to calculate the insurance premium and the indemnity. The two SL products are different in payment guarantee but have the same trigger point. The SCO policy payment guarantee is same as CCIP products. At the 75% coverage level, all SCO policies are optimal. The RP with SCO has highest dollar benefit among all the different SCO policies with $28 per acre more (Tables 3 and 4, Figure 1). However, as seen in Figure 1, the CCIP products alone have a higher dollars per acre benefit compared with a CCIP with SCO policy for all coverage levels. This result is linked to the fact that although the SCO carries the same underlying subsidy rate as the CCIP and pays on farm yields, it is triggered at the county yield, so it is less effective for risk management than a standard CCIP policy.
Table 3. Summary of Optimal Insurance Coverage for Lynn County High-Productivity Nonirrigated Cotton Farm in Dollars per Acre Benefit Using Risk Management Agency Expected County Yield Compared with No Insurance Benefit for Risk-Averse Farmer
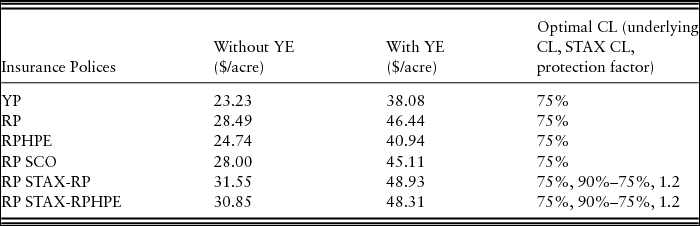
Notes: CL, coverage level; RP, Revenue Protection; RPHPE, Revenue Protection with Harvest Price Exclusion; SCO, Supplemental Coverage Option; STAX, Stacked Income Protection Plan; YE, Yield Exclusion; YP, Yield Protection.
Table 4. Results for Common Crop Insurance Provisions and Supplemental Coverage Option (SCO) Insurance Policy for Lynn County High-Productivity Nonirrigated Cotton Farm in Dollars per Acre Benefit Using Risk Management Agency Expected County Yield Compared with No Insurance Benefit for Risk-Averse Farmer
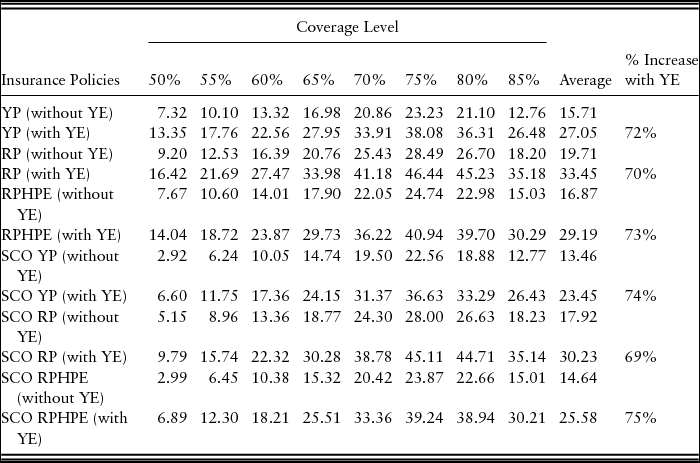
Notes: RP, Revenue Protection; RPHPE, Revenue Protection with Harvest Price Exclusion; YE, Yield Exclusion; YP, Yield Protection.
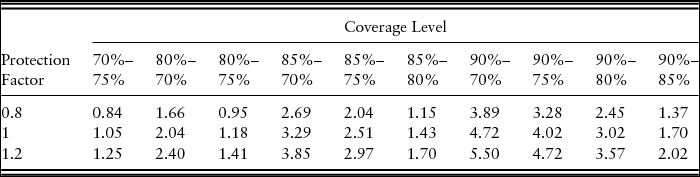
By contrast, at the 70%–90% coverage level, STAX policies generate the highest CEs at all protection factors.Footnote 20 Among the STAX policies and protection factor choices, the highest dollar benefit is $2.07 per acre for STAX-RP with 1.2 protection factor compared with RP alone (Table 5). The results from STAX-RPHPE are presented in Table 6. The STAX policy has a higher premium subsidy than the CCIP, and although triggered and paid on the county yield, the STAX policy adds revenue, on average, to the farm. Thus, it does have some, albeit small, positive net return over the premium.
Table 5. Results for Stacked Income Protection Plan–Revenue Protection Insurance for Lynn County High-Productivity Nonirrigated Cotton Farm in Dollars per Acre Benefit Using Risk Management Agency Expected County Yield Compared with No Insurance Benefit for Risk-Averse Farmer
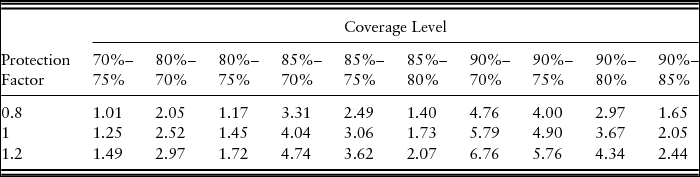
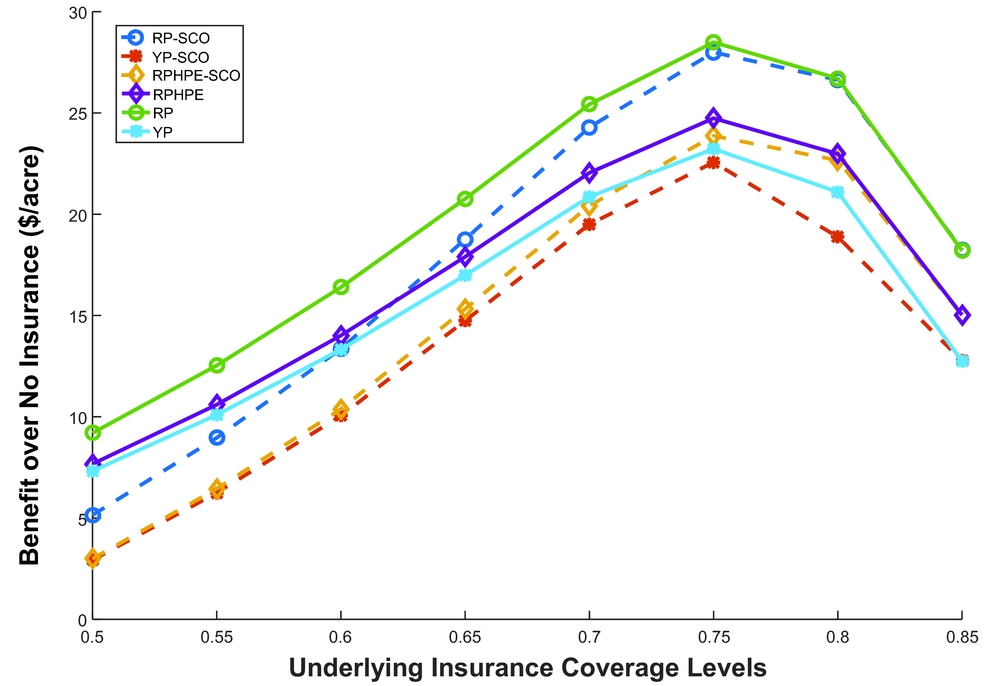
Figure 1. Dollar per Acre Benefit over No Insurance, Using Risk Management Agency Expected Yield and Coefficient of Risk Averse (r) as 2 from Common Crop Insurance Provisions Alone and Supplemental Coverage Option (SCO) for a Lynn County Nonirrigated Cotton High-Productivity Farm (notes: RP, Revenue Protection; RPHPE, Revenue Protection with Harvest Price Exclusion; YP, Yield Protection)
Table 6. Results for Stacked Income Protection Plan–Revenue Protection with Harvest Price Exclusion Insurance for Lynn County High-Productivity Nonirrigated Cotton Farm in dollars per Acre Benefit Using Risk Management Agency Expected County Yield Compared with No Insurance Benefit for Risk Averse Farmer
The choice between SCO and STAX is governed by various factors (Table 1). Figure 2 compares the dollars per acre benefit of two different SL products in combination with CCIP products. In the figure, a STAX protection factor of 100% was chosen to directly compare its benefit with SCO, as SCO has only a 100% protection factor. Figure 2 also shows all possible coverages for SCO policies. However, the figure only shows three different coverage ranges for STAX-RP (70%–85%, 75%–90%, and 75%–85%).Footnote 21 In any coverage level of underlying (CCIP) policy, STAX has higher dollar benefits per acre compared with SCO at similar SL coverages (Figure 2). This result is mostly because of a higher premium subsidy for STAX and enterprise unit insurance.
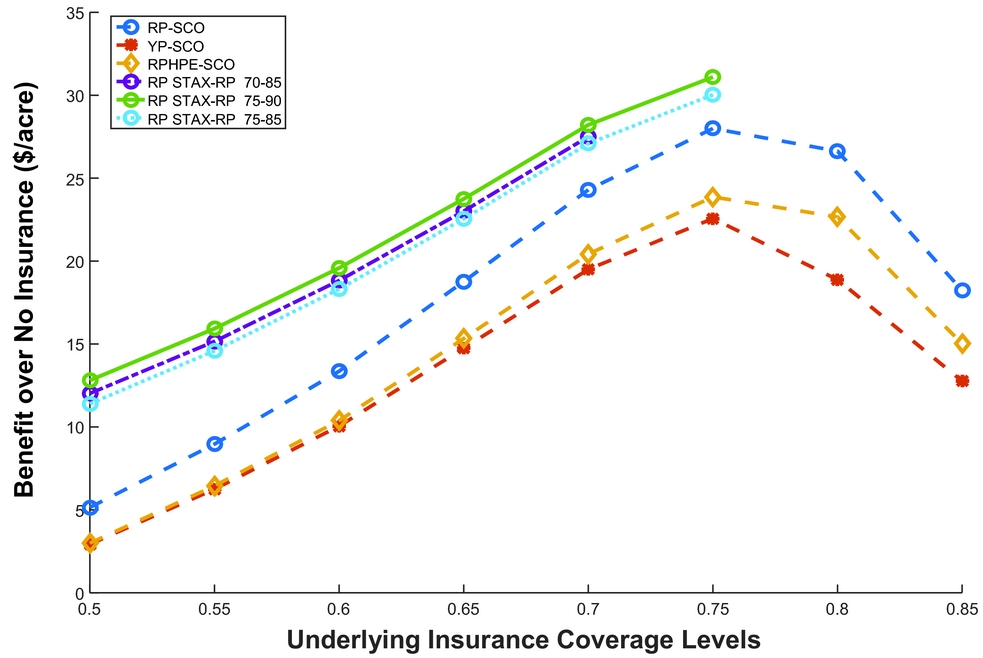
Figure 2. Dollar per Acre Benefit over No Insurance, Using Risk Management Agency Expected Yield and Coefficient of Risk Averse (r) as 2 from Shallow Loss Insurance (Supplemental Coverage Option [SCO] and Stacked Income Protection Plan [STAX]) for a Lynn County Nonirrigated Cotton High-Productivity Farm (notes: RP, Revenue Protection; RPHPE, Revenue Protection with Harvest Price Exclusion; YP, Yield Protection)
As the indemnity trigger is the same for both SL policies, the probability of receiving an indemnity is the same for SCO and STAX. Both STAX and SCO are triggered by county yield, which does not depend on farm productivity. Further, the indemnity payment for STAX is independent of farm productivity; however, the SCO indemnity payment is based on farm productivity. In this study, we found the optimal insurance choice in an enterprise unit insurance result for high- and low-productivity farms was qualitatively the same.Footnote 22 STAX is optimal because of the effect of the subsidy on the premium, while the guaranteed yield (the farm productivity) affects the indemnity payment for SCO. The low-productivity farm has, on average, a lower yield guarantee compared with an area insurance product.Footnote 23 SCO was also not optimal for the high-productivity farm.
Comparing the dollars per acre benefits among different insurance products discussed previously, CCIP alone has higher benefits than combining with SCO. However, CCIP in combination with STAX-RP has a higher net benefit than CCIP alone. The optimal insurance choice with the highest benefit per acre is underlying (CCIP) RP at the 75% coverage level with STAX-RP for 75% to 90% coverage range with a 1.2 protection factor (Table 3). The dollars per acre benefit is $31.55 from the combination of policies compared with no insurance. However, it should be noted that the added benefit of STAX, although positive, was relatively small numerically.
The YE provision does not affect the indemnity payment for STAX. However, CCIP and SCO indemnities are paid under the farm expected yield; therefore, YE increases the indemnity amount (Table 4). When YE increases the APH by 20%, the average dollars per acre benefit on all coverage levels for CCIP alone or SCO is at least 69% higher. The YE does not change the optimal coverage level choice in either high- or low-productivity farms; however, this result suggests that farmers using YE provisions could decrease their coverage level compared with previous years to get the same dollar benefits at lower average cost.Footnote 24 The YE provisions seem relevant in the Texas High Plains with respect to farmers’ incentives for higher benefits, as these counties are mostly affected by drought and have more years eligible for exclusion than in most other regions. Use of YE results in a higher APH and higher yield guarantee.
In other studies on cotton, the optimal insurance choice was RP with an 85% coverage level (Davis, Anderson, and Smith, Reference Davis, Anderson and Smith2014; Dismukes et al., Reference Dismukes, Coble, Miller and O'Donoghue2013) and 80% coverage level (Bulut and Collins, Reference Bulut and Collins2014). Similar to the results here, Bulut and Collins also found the RP with STAX is optimal at the 75% coverage level and has higher benefits in all coverage levels. Fewer cotton farmers have taken coverage levels higher than 75% than for many other crops; in 2013, only 5% of cotton farmers took a coverage level of more than 80% (Dismukes et al., Reference Dismukes, Coble, Miller and O'Donoghue2013). Cotton farmers would not be expected to change their CCIP coverage levels when taking STAX, as they normally do not take higher than 75% coverage levels.
As stated earlier, there has been low participation in the SL program. Low participation may have been a function of two primary reasons. First, the products were new and introduced late in the decision cycle (especially 2015). Lack of complete understanding by both agents and farmers likely slowed adoption. Second, soil moisture and weather were favorable for nonirrigated cotton in 2015 and 2016. This may have caused lower participation in this insurance program as producers may have anticipated small county-wide losses. Gardner and Kramer (Reference Gardner, Kramer, Hazell, Pomerada and Valdez1986) talked about increases in participation in a new program over time, but the weather and price of cotton will likely play a major role in future participation in the new SL insurance program.
7. Conclusion
In the Agricultural Act of 2014, cotton was largely removed from commodity programs, in part because of the 2009 WTO ruling. SL insurance products (SCO and STAX) were added, largely as a substitute for historical commodity programs. STAX is specifically designed for cotton farmers to give them similar potential benefits compared with historical commodity program payments as an insurance product. The trigger for the payment is county yield for STAX and SCO, while the payment is based on county yield for STAX and on farm yield for SCO. STAX offers a 4-percentage-point wider coverage range than SCO and a 20% additional protection factor, but STAX is independent of an underlying CCIP policy unlike SCO. Another policy provision is YE, which increases APH yields of the farm resulting in potentially higher yield guarantees and higher net benefits for a farmer. The addition of these insurance policies gives farmers more diverse choices to protect their agricultural risk either based on their own risk preferences or farm risk characteristics. The policies seem to increase the complexity of insurance decisions, which may have contributed to low participation.
As previous literature has suggested, the insurance premium subsidy has played a critical role in increasing participation in federal crop insurance programs. Although the SL products, especially STAX, do generate higher expected returns to farmers, they do not appear to alter optimal individual CCIP coverage choices. This result is important because it means that the program did not likely alter underlying risk management decisions and these policies were indeed likely treated as “additional” coverage rather than substitute coverage. However, despite the apparent per acre net benefits, overall participation has been low.
We found the optimal coverage level at 75% with or without YE, and the farmers were better off taking CCIP alone rather than with SCO. There are few dollars per acre more benefit when enrolled in STAX but not compared with previous commodity program benefits. Between 2003 and 2009, on average, cotton commodity program benefits were $208 per harvested acreFootnote 25 (Schnepf, Reference Schnepf2010), while in 2015, the amount was $15 per insured acre from SL (USDA-RMA, 2015a). We found the maximum net benefit from STAX was $4.47 per acre. The net benefit is likely one of the reasons for low participation in the SL program and calls for inclusion of cotton back in commodity programs. Currently, cotton farmers are taking on average 70%–75% CCIP coverage. This choice of CCIP coverage level does not seem to give much room for farmers to realize large benefits from adding SL insurance. This is worthy of serious consideration as policy makers develop future farm programs, with possible changes to subsidy levels for CCIP and SL programs and potential restructuring of other commodity programs for cotton and other crops.
Supplementary material
To view supplementary material for this article, please visit https://doi.org/10.1017/aae.2018.15












