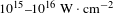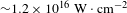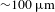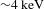1 Introduction
Laser–plasma interaction (LPI) at intensities
${\sim}10^{16}~\text{W}\,\cdot \,\text{cm}^{-2}$
is a regime of interaction dominated by parametric instabilities, where collisional absorption begins to turn off and non-collisional laser-driven instabilities – mainly stimulated Brillouin scattering (SBS), stimulated Raman scattering (SRS) and two-plasmon decay (TPD) – begin to dominate the scene. The growth of such instabilities results partly in laser absorption in the underdense plasma and partly in energy loss by inelastic light scattering (SBS, SRS). In addition, some of these instabilities (SRS and TPD) generate nonthermal ‘hot’ electrons (HE), capable of escaping the plasma, and carrying a relevant fraction of the laser energy. The strong nonlinearity of these mechanisms, the role of electron kinetic effects in their growth/damping and their mutual interplay, often giving rise to daughter instabilities, make it very hard to accurately depict the interaction scenario. Moreover, this aim is complicated by the impact of local conditions of interaction – varying in lengths of the order of the speckle size (
${\sim}\unicode[STIX]{x03BC}\text{m}$
) – and by the characteristic time of growth/damping – typically shorter than one picosecond – in plasmas which usually have dimensions of the order of 1 mm and are produced by high-energy lasers with duration of
${\sim}0.1{-}1~\text{ns}$
.
The interest in this interaction regime mainly concerns the physics of inertial confinement fusion (ICF), where the laser–plasma coupling and the generation of HE can considerably affect the implosion of the fuel pellet. In particular, accurate knowledge of parametric instabilities is crucial in the shock ignition (SI) concept[Reference Betti, Zhou, Anderson, Perkins, Theobald and Solodov1], where ignition is produced by a strong shock driven in a pre-formed millimetre-size plasma corona by a short spike (300–500 ps) at intensity
${\sim}10^{16}~\text{W}\,\cdot \,\text{cm}^{-2}$
. These interaction conditions, in fact, notably enhance the extent of parametric instabilities with respect to conventional direct-drive ICF schemes, where the laser intensity is a factor of ten to twenty lower. A further peculiarity of shock ignition is the role played by HE produced by the shock-driving spike in achieving ignition conditions. In fact, HE produced during the compression phase in conventional (direct-drive) ICF schemes are detrimental, because they preheat the fuel, increasing its entropy and therefore preventing its compression. In contrast, in SI, HE produced by the SI spike are generated at the end of the compression phase, when the target areal density
$\langle \unicode[STIX]{x1D70C}r\rangle$
is already large enough to stop the less energetic of them; in this way, they deliver their energy in the compressed corona layer, providing an extra pressure, possibly improving the compression[Reference Nora, Theobald, Betti, Marshall, Michel, Seka, Yaakobi, Lafon, Stoeckl, Delettrez, Solodov, Casner, Reverdin, Ribeyre, Vallet, Peebles, Beg and Wei2–Reference Bell and Tzoufras5]. Only the most energetic HE are expected to reach the pre-compressed fuel and enhance the fuel temperature[Reference Trela, Theobald, Anderson, Batani, Betti, Casner, Delettrez, Frenje, Glebov, Ribeyre, Solodov, Stoeckl and Stoeckl6], before the arrival of the shock driven by the laser spike. In order to assess the compression performance in SI, it is therefore decisive to investigate the amount and, above all, the energy distribution of HE. This task is strictly related to the investigation of the HE sources, mainly SRS and TPD instabilities, which produce HE with different energetic spectra and with different angular distributions. SRS usually generates HE of some tens of keV, with energy mainly depending on the density region where SRS is excited. TPD provides instead a hotter (and potentially detrimental) component, often temperatures in excess of 100 keV, by a staged acceleration mechanism occurring close to the quarter critical density region[Reference Yan, Ren, Li, Maximov, Mori, Sheng and Tsung7].
Most of the experiments devoted to investigating LPI for ICF studies have been carried out at intensities of
${\lesssim}10^{15}~\text{W}\,\cdot \,\text{cm}^{-2}$
, mainly by using 351 nm laser light, in conditions relevant for conventional direct- or indirect-drive ICF schemes[Reference Craxton, Anderson, Boehly, Goncharov, Harding, Knauer, McCrory, McKenty, Meyerhofer, Myatt, Schmitt, Sethian, Short, Skupsky, Theobald, Kruer, Tanaka, Betti, Collins, Delettrez, Hu, Marozas, Maximov, Michel, Radha, Regan, Sangster, Seka, Solodov, Soures, Stoeckl and Zuegel8, Reference Kirkwood, Moody, Kline, Dewald, Glenzer, Divol, Michel, Hinkel, Berger, Williams, Milovich, Yin, Rose, MacGowan, Landen, Rosen and Lindl9]. Due to the nonlinearity of the processes, extrapolating these results to laser intensities typical of SI is infeasible. On the other hand, the experimental investigation of parametric instabilities in SI conditions is hard, since it requires the interaction of a sub-ns pulse at intensity
${\sim}10^{16}~\text{W}\,\cdot \,\text{cm}^{-2}$
with a millimetre-size and hot (
$T_{e}>4~\text{keV}$
) plasma. Such conditions are presently attainable only at very large laser installations, such as the National Ignition Facility (NIF)[Reference Moses, Boyd, Remington, Keane and Al-Ayat10] and the Laser MegaJoule (LMJ) facility[Reference Casner, Caillaud, Darbon, Duval, Thfouin, Jadaud, LeBreton, Reverdin, Rosse, Rosch, Blanchot, Villette, Wrobel and Miquel11], which were designed for indirect-drive ICF.
A full numerical investigation of LPI in SI conditions is also impracticable because of the huge computational costs due to the large plasma size; therefore, 2D particle-in-cell simulations of LPI in this regime are presently limited to an interaction time of a few picoseconds (that is, a time much shorter than the duration of the shock ignition spike). It is worth remarking that 2D and 3D simulations are needed to model laser filamentation, spraying, cavitation and side scattering, which can be important in the SI regime. Advanced fully kinetic PIC simulations[Reference Klimo and Tikhonchuk12–Reference Riconda, Weber, Tikhonchuk and Hron14] reveal the importance of nonlinear and kinetic effects, of secondary decay processes and of competition/interplay between parametric instabilities, where all these processes govern the instability growth and make the outcome hard to predict. After a linear stage of growth, electron plasma waves (EPWs) and ionic acoustic waves (IAWs), driven respectively by SRS and SBS, enter in a nonlinear evolution, resulting in consecutive stages of damping and excitation, leading to a burst-like behaviour. In the case of EPWs, this behaviour can be produced by the ponderomotive trapping of thermal electrons or by the bowing and filamentation of EPWs into the laser speckles[Reference Yin, Albright, Rose, Bowers, Bergen, Montgomery, Kline and Fernandez15, Reference Yin, Albright, Bowers, Daughton and Rose16], resulting in a phase detuning of the waves[Reference Morales and O’Neil17] and finally in an SRS pattern of picosecond or sub-picosecond bursts. Simulations also reveal the possibility of competition between instabilities, usually ruled by laser pump depletion or because they are driven in the same density region. Particularly important is the competition between SRS and TPD in the region close to
$n_{c}/4$
, because of its impact on the energy and amount of HE generated. Recent 2D PIC simulations by Xiao et al.
[Reference Xiao, Liu, Zheng and He18] and by Weber et al.
[Reference Weber and Riconda19] showed that SRS and TPD can dominate over each other, depending on the laser intensity, density scalelength and overall plasma temperature. It is shown that the absolute SRS instability begins to dominate the scene at
$n_{c}/4$
density at temperatures higher than
${\sim}5~\text{keV}$
(that is, in conditions close to SI). Klimo et al.
[Reference Klimo and Tikhonchuk12, Reference Klimo, Psikal, Tikhonchuk and Weber13] showed also the occurrence of cavitation near
$n_{c}/4$
, resulting in a considerable absorption of laser energy and in the damping of TPD instability driven at higher plasma densities. Particular attention should be paid to stimulated Raman side scattering (SRSS), the coupling geometry where light is scattered at angles near
$90^{\circ }$
, is then refracted towards lower densities, and finally exits the plasma at large angles with respect to laser incidence. It is well known that basic theory predicts that SRSS has the lowest threshold in inhomogeneous plasmas because of the large resonant region along the transverse direction. Despite that, very few experiments have shown evidence of SRSS, which was usually explained by the large collisional absorption of side-scattered light. A recent work by Xiao et al.
[Reference Xiao, Zhuo, Yin, Liu, Zheng, Zhao and He20] revisited the theory of SRSS, including the effect of the laser beam width on the threshold of the instability, which could explain the scarcity of experimental evidence of SRSS. According to Xiao et al., SRSS, preferentially driven at low plasma densities where collisional absorption is low, can however be strong and compete with backward SRS at SI intensities, resulting in the scattering of a significant amount of laser energy.
To date, only a few experiments on LPI at SI-relevant intensities have been carried out in moderate kilojoule-class laser facilities, as for example at OMEGA[Reference Nora, Theobald, Betti, Marshall, Michel, Seka, Yaakobi, Lafon, Stoeckl, Delettrez, Solodov, Casner, Reverdin, Ribeyre, Vallet, Peebles, Beg and Wei2, Reference Theobald, Nora, Seka, Lafon, Anderson, Hohenberger, Marshall, Michel, Solodov, Stoeckl, Edgell, Yaakobi, Casner, Reverdin, Ribeyre, Shvydky, Vallet, Peebles, Beg, Wei and Betti3, Reference Theobald, Nora, Lafon, Casner, Ribeyre, Anderson, Betti, Delettrez, Frenje, Glebov, Gotchev, Hohenberger, Hu, Marshall, Meyerhofer, Sangster, Schurtz, Seka, Smalyuk, Stoeckl and Yaakobi21], LULI[Reference Goyon, Depierreux, Yahia, Loisel, Baccou, Courvoisier, Borisenko, Orekhov, Rosmej and Labaune22, Reference Depierreux, Loiseau, Michel, Tassin, Stenz, Masson-Laborde, Goyon, Yahia and Labaune23] and PALS[Reference Koester, Antonelli, Atzeni, Badziak, Baffigi, Batani, Cecchetti, Chodukowski, Consoli, Cristoforetti, De Angelis, Folpini, Gizzi, Kalinowska, Krousky, Kucharik, Labate, Levato, Liska, Malka, Maheut, Marocchino, Nicolai, O’Dell, Parys, Pisarczyk, Raczka, Renner, Rhee, Ribeyre, Richetta, Rosinski, Ryc, Skala, Schiavi, Schurtz, Smid, Spindloe, Ullschmied, Wolowski and Zaras24–Reference Batani, Antonelli, Barbato, Boutoux, Colatis, Feugeas, Folpini, Mancelli, Nicolai, Santos, Trela, Tikhonchuk, Badziak, Chodukowski, Jakubowska, Kalinowska, Pisarczyk, Rosinski, Sawicka, Baffigi, Cristoforetti, DAmato, Koester, Gizzi, Viciani, Atzeni, Schiavi, Skoric, Guskov, Honrubia, Limpouch, Klimo, Skala, Gu, Krousky, Renner, Smid, Weber, Dudzak, Krus and Ullschmied26]. Due to the lower available energy, typical SI interaction conditions were relaxed, typically resulting in colder (
${\sim}1{-}2~\text{keV}$
) or in shorter (
$L=n_{e}/(\text{d}n_{e}/\text{d}x)\sim 100~\unicode[STIX]{x03BC}\text{m}$
) inhomogeneous plasmas or otherwise in shorter laser pulses. Such experiments are unable to fully reproduce the expected LPI in the SI regime but are anyway necessary to investigate the effects of different experimental parameters on the growth of parametric instabilities and on HE generation, so that a scaling to real SI conditions becomes more reliable, in view of future full-scale SI experiments. These experiments showed that the energy lost during the interaction – due to laser reflection, SBS and SRS – can reach 40%–50% of the laser energy, depending on the irradiation geometry and on the laser intensity. Among these processes, SBS and laser back-reflectivity are usually of the order of
${\sim}10\%$
, rising to
${\sim}20\%$
when full-aperture scattering is accounted for[Reference Baton, Koenig, Brambrink, Schlenvoigt, Rousseaux, Debras, Laffite, Loiseau, Philippe, Rybeyre and Schurtz27]. Conversely, the variability of SRS reflectivity is much larger, going from a fraction of a percent, obtained in experiments using a planar geometry of interaction[Reference Goyon, Depierreux, Yahia, Loisel, Baccou, Courvoisier, Borisenko, Orekhov, Rosmej and Labaune22, Reference Baton, Koenig, Brambrink, Schlenvoigt, Rousseaux, Debras, Laffite, Loiseau, Philippe, Rybeyre and Schurtz27, Reference Hohenberger, Theobald, Hu, Anderson, Betti, Boehly, Casner, Fratanduono, Lafon, Meyerhofer, Nora, Ribeyre, Sangster, Schurtz, Seka, Stoeckl and Yaakobi28], up to 36%, obtained in spherical irradiation experiments[Reference Theobald, Nora, Seka, Lafon, Anderson, Hohenberger, Marshall, Michel, Solodov, Stoeckl, Edgell, Yaakobi, Casner, Reverdin, Ribeyre, Shvydky, Vallet, Peebles, Beg, Wei and Betti3, Reference Theobald, Nora, Lafon, Casner, Ribeyre, Anderson, Betti, Delettrez, Frenje, Glebov, Gotchev, Hohenberger, Hu, Marshall, Meyerhofer, Sangster, Schurtz, Seka, Smalyuk, Stoeckl and Yaakobi21]. Experiments seem to suggest that SRS is the main source of HE, reaching conversion efficiencies up to
${\sim}9\%$
of laser energy in spherical irradiation conditions[Reference Theobald, Nora, Seka, Lafon, Anderson, Hohenberger, Marshall, Michel, Solodov, Stoeckl, Edgell, Yaakobi, Casner, Reverdin, Ribeyre, Shvydky, Vallet, Peebles, Beg, Wei and Betti3]; recent experiments carried out at OMEGA showed that such large HE fluxes can significantly contribute to the ablation pressure[Reference Nora, Theobald, Betti, Marshall, Michel, Seka, Yaakobi, Lafon, Stoeckl, Delettrez, Solodov, Casner, Reverdin, Ribeyre, Vallet, Peebles, Beg and Wei2], providing an extra pressure as large as
${\sim}30\%$
.
In recent years, we investigated LPI and shock generation at the Prague Asterix Laser System (PALS) facility by using a 300 ps laser pulse at
$3\unicode[STIX]{x1D714}_{0}$
irradiation (
$\unicode[STIX]{x1D706}_{0}=438~\text{nm}$
). The laser energy of
${\sim}250~\text{J}$
enabled irradiation of a
${\sim}2~\text{keV}$
plasma with scalelength
$L=n_{e}/(\text{d}n_{e}/\text{d}x)\sim 100~\unicode[STIX]{x03BC}\text{m}$
, at a maximum laser intensity of
${\sim}6\times 10^{15}~\text{W}\,\cdot \,\text{cm}^{-2}$
. Experimental data yielded a detailed description of the extent and timing of parametric instabilities[Reference Cristoforetti, Colatis, Antonelli, Atzeni, Baffigi, Batani, Barbato, Boutoux, Dudzak, Koester, Krousky, Labate, Nicolai, Renner, Skoric, Tikhonchuk and Gizzi29, Reference Cristoforetti, Antonelli, Atzeni, Baffigi, Barbato, Batani, Boutoux, Colaitis, Dostal, Dudzak, Juha, Koester, Marocchino, Mancelli, Nicolai, Renner, Santos, Schiavi, Skoric, Smid, Straka and Gizzi30], in particular of SRS, and enabled us to establish a correlation with the measured HE energy distribution.
In this paper we investigate LPI and HE generation of the full energy (
${\sim}650~\text{J}$
) PALS laser pulse at
$1\unicode[STIX]{x1D714}_{0}$
irradiation (
$\unicode[STIX]{x1D706}_{0}=1314~\text{nm}$
), resulting in a maximum intensity of
${\sim}1.2\times 10^{16}~\text{W}\,\cdot \,\text{cm}^{-2}$
, a value seldom reached in experiments. In such irradiation conditions the plasma is heated to a temperature in excess of 4 keV, which is crucial for our studies because of the strong temperature dependence of the threshold and the damping of parametric instabilities (and therefore their respective weights), of the density where they are driven, and finally of the HE energy distribution. Moreover, the use of infrared laser light resulted in an even larger value of laser irradiance
$I\unicode[STIX]{x1D706}^{2}\approx 2\times 10^{16}~\text{W}\,\cdot \,\unicode[STIX]{x03BC}\text{m}^{2}\,\cdot \,\text{cm}^{-2}$
, enhancing ponderomotive effects on quivering electrons and nonlinear effects in their dynamics. We therefore believe that the interaction regime explored here gives valuable information for the understanding of LPI in SI conditions. Besides, it is worth noting that while conventional ICF schemes make use of ultraviolet (
$3\unicode[STIX]{x1D714}$
) lasers, in the shock ignition scheme
$2\unicode[STIX]{x1D714}$
or even
$1\unicode[STIX]{x1D714}$
lasers could in principle be considered for the final irradiation spike driving the strong shock[Reference Atzeni, Marocchino and Schiavi31].
2 Experimental setup
The laser pulse (300 ps), used in the fundamental mode (
$\unicode[STIX]{x1D706}_{0}=1314~\text{nm}$
), was smoothed by a random phase plate and focused at normal incidence on a flat thin target by a
$f/\#2$
optical system. Laser energy ranged from 630 to 660 J. Accurate imaging and calorimetry were set up to measure the effective energy enclosed in the 100
$\unicode[STIX]{x03BC}\text{m}$
full-width at half-maximum (FWHM) Gaussian focal spot and to calculate the peak laser intensity
$I=1.2\times 10^{16}~\text{W}\,\cdot \,\text{cm}^{-2}$
.
Thin multilayer targets were used. The front layer, namely the interaction layer, with thickness ranging from 10 to
$180~\unicode[STIX]{x03BC}\text{m}$
, was made of Parylene-C plastic, to mimic the low-
$Z$
ablation layer in ICF targets. A ‘tracer’ layer of titanium,
$10~\unicode[STIX]{x03BC}\text{m}$
thick, was used to characterize the HE propagating into the target through K
$_{\unicode[STIX]{x1D6FC}}$
spectroscopy. A final
$25~\unicode[STIX]{x03BC}\text{m}$
thick Al layer was used for the measurement of shock breakout time, with the purpose of estimating shock velocity and driving pressure. A companion paper describing results of shock hydrodynamics is in preparation[Reference Antonelli, Trela, Barbato, Boutoux, Nicolai, Batani, Tikhonchuk, Mancelli, Atzeni, Schiavi, Baffigi, Cristoforetti, Viciani, Gizzi, Smid, Renner, Dostal, Dudzak, Juha and Krus32].
Figure 1. Experimental setup used for the investigation of parametric instabilities.
A scheme of the optical diagnostics used for investigating the parametric instabilities is reported in Figure 1. The backscattered light collected by the focusing lens was spectrally filtered and characterized by two calorimeters. One of them measured the energy backscattered in the spectral range around
$\unicode[STIX]{x1D706}\approx 1314~\text{nm}$
, due to laser reflection and SBS, and the other measured the energy in the range 1600–2500 nm, due to SRS. The retrieval of backscattered energy was made possible by an accurate calibration of the spectral transmission of the optical line in the infrared range. Light scattered by SRS outside the cone of the focusing lens was also collected by means of an
$f/\#7$
optical system, at angles spanning from
${\sim}20^{\circ }$
, close to the backscattering cone, to
$62^{\circ }$
, and sent to a near-infrared (NIR) spectrometer NIRQuest Ocean Optics via an IR low-OH optical fibre. The spectral range covered by the NIR spectrometer was 1100–2530 nm, thus excluding the
$\unicode[STIX]{x1D714}_{0}/2$
light at
$\unicode[STIX]{x1D706}=2628~\text{nm}$
and the longer wavelengths. Light emission in the UV–Vis range, including harmonics and half-harmonics of laser light, was collected by means of an
$f/\#8$
optical system at an angle of
$30^{\circ }$
. A pick-off reflection from this line was conveyed by an optical fibre to an additional Ocean Optics spectrometer, covering the spectral range 200–900 nm. The remaining part of the light was spectrally dispersed by a Czerny–Turner monochromator, and relayed onto the entrance slit of a Hamamatsu C7700 optical streak camera. This setup allowed time-resolution of the
$3/2\unicode[STIX]{x1D714}_{0}$
harmonics, in a spectral window of 60 nm at a maximum temporal resolution of 25 ps, calculated by considering the temporal spread produced by the spectrometer[Reference Visco, Drake, Froula, Glenzer and Pollock33] and the time resolution of the streak camera. As will be shown below, half-harmonics of laser light reveal information on the timing of both TPD and SRS.
K
$_{\unicode[STIX]{x1D6FC}}$
emission of titanium was produced by the collisions of HE with the Ti tracer layer, resulting in the
$2\text{p}\rightarrow 1\text{s}$
K-shell fluorescence. K
$_{\unicode[STIX]{x1D6FC}}$
spectroscopy was carried out by using a spherically bent crystal of quartz (211) and image plates (BAS-MS), or alternatively Kodak AA400 X-ray film, as detectors. The spectral resolution of the line profile allowed us to subtract the continuum background emission, mainly due to Bremsstrahlung and recombination continuum. A Bremsstrahlung cannon spectrometer (BCS) using K-edge and differential filtering (14 filters of increasing
$Z$
from Al to Pb) was also used with imaging plates to measure the X-ray spectrum and, indirectly, calculate the temperature of the HE distribution. The BCS was looking at the front side of the target at
$30^{\circ }$
from the laser axis.
Figure 2. Instantaneous values of electron temperature
$T_{e}$
(red squares) and density scalelength
$L$
(blue stars) in the density range
$0.05{-}0.25\,n_{c}$
, as obtained by CHIC hydrosimulations in the experimental conditions of the interaction. The dashed line indicates the laser pulse profile.
3 Interaction conditions
The plasma density where parametric instabilities are driven and their timing depend on local and instantaneous plasma conditions (temperature and density scalelength) and the laser intensity. Interaction conditions were modelled by radiative-hydrodynamic simulations carried out with the codes CHIC[Reference Breil, Galera and Maire34] and DUED[Reference Atzeni, Schiavi, Califano, Cattani, Cornolti, Del Sarto, Liseykina, Macchi and Pegoraro35]. In the CHIC code, the onset of SRS and TPD processes as well as the generation of HE was also implemented[Reference Colaitis, Duchateau, Ribeyre, Maheut, Boutoux, Antonelli, Nicolai, Batani and Tikhonchuk36] by means of appropriate scaling laws and using local and instantaneous values of laser intensity and plasma parameters. The code, therefore, accounts for the interplay between TPD/SRS and the hydrodynamics of the plasma.
The resulting values of electron temperature and density scalelength
$L=n_{e}/(\text{d}n_{e}/\text{d}x)$
, in the density range of interest for TPD and SRS instabilities (0.05–0.25
$n_{c}$
), are plotted in Figure 2 at different interaction times. While the plasma temperature reaches the maximum value approximately a hundred picoseconds after the laser peak, and successively falls, the density scalelength monotonically increases till the end of the interaction. Simulations show that collisional absorption is only
${\sim}9\%$
, due to the high intensity and the long wavelength of the laser (high
$I\unicode[STIX]{x1D706}^{2}$
). The energy converted into HE is also a few percent (
$\unicode[STIX]{x1D716}_{HE}^{TPD}=1.1\%$
,
$\unicode[STIX]{x1D716}_{HE}^{SRS}=2.3\%$
), suggesting that non-collisional absorption by parametric instabilities is comparable to collisional absorption. It is worth noting that the extent of parametric instabilities is certainly underestimated by the code, as side-scattering SRS, inflationary and secondary scattering processes are neglected. Also, due to the scarcity of experimental results for infrared laser light, scaling laws in this regime should be taken with caution. According to the model implemented in CHIC, the temperature of the two HE populations is 39 keV for SRS and 83 keV for TPD. In the experiment, the HE energy distribution was estimated by the measurements of K
$_{\unicode[STIX]{x1D6FC}}$
and Bremsstrahlung X-ray emission. Experimental data of K
$_{\unicode[STIX]{x1D6FC}}$
emission could be satisfactorily reproduced with GEANT4 Monte Carlo simulations by using a two-temperature distribution for the HE energy, with temperature values of 40 keV and 85 keV, in agreement with the values given by CHIC simulations. The experimental calibration of the reflectivity of the crystal used for the Ti K
$_{\unicode[STIX]{x1D6FC}}$
spectroscopy also allowed us to calculate the energy conversion efficiency of HE, giving
$\unicode[STIX]{x1D716}_{HE}=5.3\%\pm 2\%$
. Further details on the experimental HE characterization in this experiment can be found in a companion paper, now in preparation[Reference Antonelli, Trela, Barbato, Boutoux, Nicolai, Batani, Tikhonchuk, Mancelli, Atzeni, Schiavi, Baffigi, Cristoforetti, Viciani, Gizzi, Smid, Renner, Dostal, Dudzak, Juha and Krus32].
The plasma conditions, determined by plasma hydrodynamics, and the resulting interaction scenario depicted above, can be significantly modified by considering micrometre-scale variations of temperature and density, which are produced by the profile smoothing of the laser beam. The use of a random phase plate, in fact, limits the longitudinal and the transverse spatial coherence of the beam, subdividing the profile into small beamlets with random phases; according to simple calculations[Reference Batani, Bleu and Lower37], in our experimental conditions this gives rise to the formation of
${\sim}10^{4}$
speckles of size
$3.2~\unicode[STIX]{x03BC}\text{m}\times 3.2~\unicode[STIX]{x03BC}\text{m}\times 14~\unicode[STIX]{x03BC}\text{m}$
in the focal volume. The expected intensity distribution in the speckle ensemble, produced by the interference of the various beamlets[Reference Rose and Dubois38], is exponential
$f(I)\propto \text{exp}(-I/I_{av})/I_{av}$
, where
$I_{av}$
is the average laser intensity, which results in a tail of local high intensities reaching
${\sim}10^{17}~\text{W}\,\cdot \,\text{cm}^{-2}$
in a fraction of the speckles. Local laser power into the speckles is therefore 1–10 GW – that is, well above the critical power for ponderomotive filamentation (
$P_{c}\approx 0.2{-}0.6~\text{GW}$
at relevant plasma temperatures[Reference Pesme, Huller, Myatt, Riconda, Maximov, Tikhonchuk, Labaune, Fuchs, Depierreux and Baldis39]). This implies that filamentation is rapidly driven into the speckles, further enhancing the local laser intensity and plasma temperature and modifying the plasma density profiles, in times of the order of a few picoseconds. Filamentation instability is therefore expected to strongly affect the onset and growth of parametric instabilities. Ponderomotive filamentation, not included in the CHIC simulations, is here investigated by particle-in-cell (PIC) simulations of LPI carried out with plasma parameters (density, temperature) defined by hydrosimulations, as shown in the following.
4 Reflectivity, backward- and side-stimulated Raman scattering
Light backscattered in the focusing cone was dominated by laser reflection and SBS light (
$\unicode[STIX]{x1D706}\approx 1314~\text{nm}$
), consisting of 14%–20% of the laser energy, where the relative fractions of SBS and laser light could not be determined. A significant fraction of laser energy
${\sim}$
0.6%–4% consisted also of light back-reflected in the spectral range
$1600{-}2500~\text{nm}$
. This radiation was produced by convective backward SRS (BRS) occurring at densities lower than
$n_{c}/4$
. Infrared light at longer wavelengths, including
$\unicode[STIX]{x1D714}_{0}/2$
light due to absolute SRS driven at
$n_{c}/4$
density, could not be quantified because of the poor transmissivity of the backscattering optical line.
Figure 3. Typical time-integrated SRS spectra acquired at
$\unicode[STIX]{x1D703}=20^{\circ }$
(BRS) and
$\unicode[STIX]{x1D703}=50^{\circ }$
(SRSS).
Typical time-integrated spectra of SRS scattered light up to
$\unicode[STIX]{x1D706}=2530~\text{nm}$
acquired at different angles are reported in Figure 3. Due to the small
$f/\#$
of the focusing lens, the spectrum measured at
$\unicode[STIX]{x1D703}=20^{\circ }$
, very close to the focusing cone, is likely comparable to the BRS spectrum. Considering a plasma temperature of
${\sim}4~\text{keV}$
, as given by hydrosimulations for times close to the laser peak, the measured emission originates from BRS driven in the range of densities 0.14–0.20
$n_{c}$
, with a probable maximum emission coming from
$n_{e}\approx 0.17{-}0.18\,n_{c}$
(Figure 4). It is worth noting that the spectra acquired by the IR spectrometer do not allow one to determine the highest density where BRS is driven, because of the limited spectral range of our IR spectrometer. However, temperature values of
${\sim}4~\text{keV}$
fix the maximum density to
${\sim}0.23\,n_{c}$
– that is, close to the density where absolute TPD/SRS is also driven (see section below). Moreover, streaked spectra shown in Section 6, acquired at a slightly larger angle (
$30^{\circ }$
) confirm that the stronger SRS emission comes from the
$n_{e}\approx 0.17{-}0.18\,n_{c}$
region (later in Figure 7). Since the Landau cutoff condition for large damping,
$k_{e}\unicode[STIX]{x1D706}_{D}\approx 0.3$
, corresponds to densities of
${\sim}0.13\,n_{c}$
(
$\unicode[STIX]{x1D706}_{SRS}\approx 2200~\text{nm}$
,
$k_{e}=1.41\,\unicode[STIX]{x1D714}_{0}/c$
) and
${\sim}0.15\,n_{c}$
(
$\unicode[STIX]{x1D706}_{SRS}\approx 2350~\text{nm}$
,
$k_{e}=1.32\,\unicode[STIX]{x1D714}_{0}/c$
), for plasma temperatures of 3 keV and 4 keV, respectively, it is evident that BRS is limited by this effect in the low-plasma-density region. In this way, Landau damping limits the BRS growth to higher densities when plasma temperature is large. This feature agrees with the shift of the BRS peak region from 0.12
$n_{c}$
to 0.18
$n_{c}$
, obtained by comparing the results in shots at
$3\unicode[STIX]{x1D714}_{0}$
irradiation[Reference Cristoforetti, Antonelli, Atzeni, Baffigi, Barbato, Batani, Boutoux, Colaitis, Dostal, Dudzak, Juha, Koester, Marocchino, Mancelli, Nicolai, Renner, Santos, Schiavi, Skoric, Smid, Straka and Gizzi30], where maximum plasma temperature was 2–2.5 keV, with the ones obtained in the present work.
While the IR spectra acquired at
$\unicode[STIX]{x1D703}=62^{\circ }$
did not show any appreciable emission, the ones acquired at
$\unicode[STIX]{x1D703}=50^{\circ }$
(Figure 3) showed evidence of SRSS, suggesting that this instability was driven at lower plasma densities and fell at higher densities where BRS became dominant. According to the spectra, SRSS was driven at densities 0.08–0.17
$n_{c}$
, with a maximum growth rate around
$n_{e}\sim 0.12\,n_{c}$
(Figure 4). Considering light refraction across the density distribution obtained by CHIC simulations, SRSS light was emitted at an angle
$65^{\circ }<\unicode[STIX]{x1D703}^{\prime }<90^{\circ }$
, in agreement with the PIC simulations of Xiao et al.
[Reference Xiao, Zhuo, Yin, Liu, Zheng, Zhao and He20]. The side-scattered EPWs excited at the lower densities (
$\unicode[STIX]{x1D706}_{SRSS}\approx 2000~\text{nm}$
,
$k_{e}=1.12\,\unicode[STIX]{x1D714}_{0}/c$
) correspond to
$k_{e}\unicode[STIX]{x1D706}_{D}\approx 0.3$
for a plasma temperature
$T_{e}\approx 4~\text{keV}$
, as expected at times near the laser peak; this suggests that SRSS, as BRS, is limited at lower densities by Landau damping.
Figure 4. Scheme of regions of density where parametric instabilities are driven.
A deeper insight into the experimental data can be obtained by calculating the thresholds of BRS and SRSS at the densities of interest. According to Liu et al.
[Reference Liu, Rosenbluth and White40], the BRS threshold can be expressed by
$(\unicode[STIX]{x1D708}_{0}/c)^{2}>1/(k_{0}L)$
, where
$\unicode[STIX]{x1D708}_{0}$
is the quiver velocity of an electron in the laser field and
$L$
is the density scalelength. Taking
$L=75~\unicode[STIX]{x03BC}\text{m}$
, i.e. the expected scalelength value at the laser peak and
$k_{0}=(\unicode[STIX]{x1D714}_{0}/c)\sqrt{1-(\unicode[STIX]{x1D714}_{p}/\unicode[STIX]{x1D714}_{0})^{2}}\approx 0.98(\unicode[STIX]{x1D714}_{0}/c)$
, corresponding to the density
$n_{e}/n_{c}=0.18$
, given by the spectral peak in the BRS spectrum, we obtain the threshold intensity
$I_{BRS}>2.7\times 10^{15}~\text{W}\,\cdot \,\text{cm}^{-2}$
. This value is approximately six times lower than the average intensity at the laser peak, and much lower than the local intensity expected from filamentation and in high-intensity speckles. For calculating the SRSS threshold, as pointed out by Xiao et al.
[Reference Xiao, Zhuo, Yin, Liu, Zheng, Zhao and He20], we have to account for the finite beam size that limits the instability gain growing in the transverse direction. This mechanism results in a threshold much higher than the classical one and can explain why SRSS is seldom observed in the experiments. According to Ref. [Reference Xiao, Zhuo, Yin, Liu, Zheng, Zhao and He20], in our case the threshold can be expressed as
$$\begin{eqnarray}\displaystyle \frac{\unicode[STIX]{x1D708}_{0}}{c}>40\left(\frac{V_{cs}}{D}\right)\left(\frac{\unicode[STIX]{x1D714}_{0}-\unicode[STIX]{x1D714}_{p}}{\unicode[STIX]{x1D714}_{p}}\right)^{1/2}\left(\frac{1}{k_{e}c}\right), & & \displaystyle\end{eqnarray}$$
where
$D$
is the focal spot diameter,
$k_{e}$
is the EPW wavevector and
$V_{cs}$
is the convective velocity of scattered light into the transverse direction. In turn
$V_{cs}=c^{2}k_{s}/\unicode[STIX]{x1D714}_{s}$
, where the subscript
$s$
refers to the scattered light. By taking
$D=100~\unicode[STIX]{x03BC}\text{m}$
and
$n_{e}/n_{c}=0.12$
, as obtained in the experiment, we obtain an intensity threshold
$I_{SRSS}>6.3\times 10^{15}~\text{W}\,\cdot \,\text{cm}^{-2}$
, which is overcome during the interaction. We have to consider that convective SRSS grows while the scattered light propagates transversally through many speckles; it is therefore more correct to consider the average laser intensity and not the local intensity, which can be somewhere higher. This threshold is quite large, suggesting that it was not probably overcome in many of the experiments devoted to ICF, which explains why SRSS was not observed except in very few works. This also suggests that in SI conditions SRSS may result in a significant amount of energy scattered at large angles and should be taken into account. It is interesting also to calculate the SRSS threshold intensity at higher densities, where BRS is observed to dominate in the experiment. By taking the density
$n_{e}/n_{c}=0.18$
, considered above for the BRS, we obtain an SRSS threshold
$I_{SRSS}>4\times 10^{15}~\text{W}\,\cdot \,\text{cm}^{-2}$
. Despite this value being overcome during the interaction, it is clear that the SRSS gain at this density is lower than the BRS gain. Furthermore, while the envelope laser intensity has to be considered for SRSS, the local intensity given by filamentation and by the high-intensity tail into the speckles has to be considered for BRS. This is due to the fact that convective BRS instability grows in the longitudinal direction – that is, along and not across the speckles. These considerations make it clear that, at higher plasma densities, BRS modes are strongly favoured and damp the SRSS modes. This is in agreement with the experimental results.
5 Half-integer harmonic spectra
A valuable tool for investigating TPD and SRS is the observation of half-integer harmonic spectra, produced by the nonlinear coupling of laser light (
$\unicode[STIX]{x1D714}_{0}$
) or integer harmonics (
$2\unicode[STIX]{x1D714}_{0}$
,
$3\unicode[STIX]{x1D714}_{0}$
, …) with EPWs driven by the instabilities. A UV–Vis time-integrated spectrometer allowed us to measure
$3/2\unicode[STIX]{x1D714}_{0}$
,
$5/2\unicode[STIX]{x1D714}_{0}$
and
$7/2\unicode[STIX]{x1D714}_{0}$
spectra, which will be discussed in the present section. In the next section, the time-resolved spectrum of
$3/2\unicode[STIX]{x1D714}_{0}$
, acquired with an optical streak camera, will be discussed.
Figure 5. Time-integrated half-integer harmonic spectra plotted versus the shift with respect to their nominal frequency. Dashed, red and green lines correspond to the peaks produced by Thomson scattering with EPWs driven by TPD, BRS and SRSS, respectively.
All the half-integer harmonic spectra exhibited several peaks, produced by different instabilities or by instabilities driven at different densities. In Figure 5 time-integrated half-integer harmonic spectra are plotted versus the shift with respect to their nominal frequency, for a fruitful comparison of the spectral position of the different peaks. Spectra refer to the same shot of the BRS spectrum reported in Figure 3. The two inner peaks (dashed lines), clearly visible in the
$3/2\unicode[STIX]{x1D714}_{0}$
spectrum and just appearing in higher-order half-integer harmonics, are produced by Thomson scattering of the laser light and higher laser harmonics with the EPWs driven by TPD or absolute SRS (aSRS) instabilities at densities close to
$n_{c}/4$
. The double-hump structure of the 3/2
$\unicode[STIX]{x1D714}_{0}$
emission is usually considered as a spectral signature of the TPD instability. In principle, however, it could also be generated by the presence of both Thomson up-scattering of laser light (
$\unicode[STIX]{x1D714}_{0}+\unicode[STIX]{x1D714}_{e}$
) and Thomson down-scattering of the
$2\unicode[STIX]{x1D714}_{0}$
light (
$2\unicode[STIX]{x1D714}_{0}-\unicode[STIX]{x1D714}_{e}$
) with the EPW generated by absolute SRS instability. According to the theory, when driven at
$n_{e}\approx n_{c}/4$
as in the present experiment (see below), TPD and SRS can also coalesce in a hybrid TPD/SRS instability[Reference Afeyan and Williams41], as claimed in the interpretation of some experimental works[Reference Seka, Afeyan, Boni, Goldman, Short, Tanaka and Johnston42]. In the conditions of temperature and density profiles expected in this experiment, the threshold of TPD is lower than that of absolute SRS, therefore suggesting a faster growth of the former instability, leading to a prevalence of TPD or eventually to a hybrid instability rather than to a pure aSRS. The frequency shift of TPD blue and red EPWs from the central frequency shift
$\unicode[STIX]{x1D714}_{0}/2$
is given by
$|\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D714}|/\unicode[STIX]{x1D714}_{0}=(9/4)(v_{th}^{2}/c^{2})\unicode[STIX]{x1D705}$
, where
$\unicode[STIX]{x1D705}=\boldsymbol{k}_{B}\,\cdot \,\boldsymbol{k}_{0}/k_{0}^{2}-1/2$
,
$\boldsymbol{k}_{B}$
is the blue EPW wavevector and
$v_{th}$
is the thermal velocity. For large plasma temperatures, corrections to this formula should be applied by considering the relativistic modification of the Langmuir wave dispersion relation[Reference Xiao, Liu, Zheng and He18]. Detailed calculations for a plasma temperature
$T_{e}\approx 3{-}4~\text{keV}$
, as given by hydrosimulations at times close to the laser peak, show that the measured frequency shift of these peaks,
$\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D714}/\unicode[STIX]{x1D714}_{0}=(0.5{-}1.5)\times 10^{-2}$
, corresponds to absolute TPD driven at densities
$n_{e}\approx 0.245\,n_{c}$
(Figure 4). A similar density would be obtained by considering absolute SRS and SRS/TPD hybrid modes, since in all the cases
$k_{e}\approx k_{0}$
. More details on the timing of such instabilities will be provided by time-resolved spectra, discussed in the next section. The peaks at larger shifts cannot be produced by TPD EPWs, since they would be strongly Landau damped at the expected plasma temperatures (
$k_{e}\unicode[STIX]{x1D706}_{D}\approx 0.4{-}0.8$
). The only possibility is that such peaks were produced by Thomson scattering of integer-harmonic light (
$2\unicode[STIX]{x1D714}_{0}$
,
$3\unicode[STIX]{x1D714}_{0}$
,
$4\unicode[STIX]{x1D714}_{0}$
), strongly visible in the acquired spectra, with the EPWs driven by backward- and side SRS. The generation of
$2\unicode[STIX]{x1D714}_{0}$
and higher harmonics is usually associated to the nonlinear interaction of laser light with plasma waves excited near the critical density, and depends critically on plasma steepness, laser intensity and laser polarization[Reference Baffigi, Cristoforetti, Fulgentini, Giulietti, Koester, Labate and Gizzi43, Reference Gizzi, Giulietti, Giulietti, Audebert, Bastiani, Geindre and Mysyrowicz44]; the presence of such peaks is therefore indirect evidence that a fraction of laser light reaches the critical density surface. The coupling combinations are reported in Figure 5, where the peaks on the blue side of the nominal half-harmonic frequencies are produced by Thomson down-scattering, while the peaks on the red side are due to Thomson up-scattering processes. It is worth noting that the spectral profile of the different peaks is strongly affected by the geometrical matching conditions, such as the angle of acquisition (
$\unicode[STIX]{x1D703}=30^{\circ }$
), the angle of EPW propagation and the direction of propagation of matching integer-harmonic light. In this way, geometrical parameters result in a distortion of the real spectral distribution of EPWs driven by SRS at different plasma densities. Coupling effects can therefore explain the discrepancies between the corresponding peaks in the different half harmonics. In some cases, a small EPW propagation can improve the matching of light and EPW wavevector; in other cases, Thomson scattering with secondary EPWs produced by Langmuir decay instability (LDI), which could be easily driven in these interaction conditions, could also generate the observed half-harmonic peaks. A typical scheme of Thomson scattering geometry is sketched in Figure 6; it refers to the up-scattering process of
$3\unicode[STIX]{x1D714}_{0}$
harmonic light with the EPW driven by SRSS at
$n_{e}\approx 0.12\,n_{c}$
, resulting in the generation of
$7/2\unicode[STIX]{x1D714}_{0}$
light. In this case, it is evident that the scattering geometry involving the secondary EPW produced by LDI, represented by dotted vectors, easily generates
$7/2\unicode[STIX]{x1D714}_{0}$
light more compatible with the angle of observation of the spectrometer (
$\unicode[STIX]{x1D703}=30^{\circ }$
). The refraction of the light across the density plasma profile, probably also including density fluctuations, could however strongly mitigate the geometrical constraints due to matching conditions, making it quite hard to determine the occurring processes.
Figure 6. Geometry of the Thomson up-scattering of
$3\unicode[STIX]{x1D714}_{0}$
harmonic light with the EPW driven by SRSS at
$n_{e}\approx 0.12\,n_{c}$
. The dotted vectors refer to the up-scattering geometry involving the secondary EPW produced by LDI.
The blue-side feature in the
$3/2\unicode[STIX]{x1D714}_{0}$
spectra (right red line) is clearly visible also in
$5/2\unicode[STIX]{x1D714}_{0}$
and
$7/2\unicode[STIX]{x1D714}_{0}$
spectra and is peaked at a shift
$\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D714}/\unicode[STIX]{x1D714}_{0}\approx 0.03{-}0.05$
. This feature is produced by Thomson down-scattering of
$2\unicode[STIX]{x1D714}_{0}$
light (and of
$3\unicode[STIX]{x1D714}_{0}$
and
$4\unicode[STIX]{x1D714}_{0}$
light in the corresponding
$5/2\unicode[STIX]{x1D714}_{0}$
and
$7/2\unicode[STIX]{x1D714}_{0}$
spectra) by SRS EPWs with energy
$\unicode[STIX]{x1D714}_{e}\approx 0.45{-}0.47~\unicode[STIX]{x1D714}_{0}$
. Such EPWs, in turn, correspond to backscattered SRS light peaked at
$\unicode[STIX]{x1D706}\approx 2400{-}2480~\text{nm}$
, which is exactly the spectral range of the peaks observed by the IR spectrometer (black curve in Figure 3). This is a confirmation that such a peak is produced by the light coupling with BRS EPWs, driven at densities
$n_{e}\approx 0.17{-}0.18\,n_{c}$
. The same EPWs give rise to the left red peak (with the same shift) in the
$5/2\unicode[STIX]{x1D714}_{0}$
spectra (left red line) by Thomson up-scattering of
$2\unicode[STIX]{x1D714}_{0}$
light. It can also be seen that the red peak with the same shift, due to the combination (
$\unicode[STIX]{x1D714}_{0}+\unicode[STIX]{x1D714}_{e}$
), is not visible in the
$3/2\unicode[STIX]{x1D714}_{0}$
spectrum plotted in Figure 5; in other shots, the peak is visible but it is usually less intense than the corresponding blue one. To be observed at an angle of
$30^{\circ }$
, SRS EPWs should match with laser light
$\unicode[STIX]{x1D714}_{0}$
propagating almost perpendicularly to the laser incidence direction; the absence or low intensity of this peak can thus possibly be explained by the scarcity of laser light which is side-scattered in the plasma.
The spectrum of
$7/2\unicode[STIX]{x1D714}_{0}$
exhibits light emitted with much larger frequency shift values,
$-0.12<\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D714}/\unicode[STIX]{x1D714}_{0}<0.18$
. This emission, labelled with green lines in Figure 5, is produced by Thomson scattering of
$3\unicode[STIX]{x1D714}_{0}$
and
$4\unicode[STIX]{x1D714}_{0}$
light with EPWs generated by SRS at low plasma densities. The extreme values of frequency shift correspond to EPWs with energy
$\unicode[STIX]{x1D714}_{e}\approx 0.35{-}0.38~\unicode[STIX]{x1D714}_{0}$
, giving rise to scattered SRS light with
$\unicode[STIX]{x1D706}\approx 2000{-}2100~\text{nm}$
. These wavelengths correspond to the edge of the red spectrum in Figure 3, suggesting that these features are produced by Thomson scattering with EPWs at low densities (0.08–0.17
$n_{c}$
) driven by SRSS. Peaks originating from SRSS at low plasma densities are absent in
$3/2\unicode[STIX]{x1D714}_{0}$
and
$5/2\unicode[STIX]{x1D714}_{0}$
spectra. It can be shown that
$2\unicode[STIX]{x1D714}_{0}$
and
$3\unicode[STIX]{x1D714}_{0}$
light propagating in the low-density region at large angles (
$\unicode[STIX]{x1D703}>55^{\circ }$
) is needed to produce such features, while these constraints are relaxed for the formation of
$7/2\unicode[STIX]{x1D714}_{0}$
SRSS peaks. We therefore speculate that the scarcity of large-angle scattered light can explain the experimental results.
6 Timing of TPD and SRS instabilities
Time-resolved spectroscopy of three-halves harmonics is here used for investigating the growth of TPD and BRS along the plasma density profile. Two distinct spectra are reported in Figure 7, showing typical features observed in the various shots. The spectra obtained by the intensity lineout in the different windows reported in the figure clearly exhibit the presence and the temporal evolution of the peaks already discussed in the previous section.
Figure 7. Time-resolved
$3/2\unicode[STIX]{x1D714}_{0}$
spectra. The time spanned across the vertical axis is 500 ps, with a time resolution of 25 ps. The laser pulse profile is indicated by the red curve and the peak time by the yellow dashed line. The spectra on the right are obtained by the lineout in windows a, b and c.
The two peaks produced by EPWs at density close to
$n_{c}/4$
due to TPD (or hybrid TPD/aSRS) with the smaller shift with respect to
$\unicode[STIX]{x1D706}=876~\text{nm}$
, begin to grow
${\sim}100{-}150~\text{ps}$
before the laser peak (yellow dashed line in the figure) – that is, in the leading part of the pulse. An accurate analysis of the splitting of these peaks at early times suggests that such instability begins to grow at a density
$n_{e}\approx 0.247\,n_{c}$
when the temperature is around 2 keV. After the onset of the instability, the distance between the peaks increases with time; this shift is mainly produced by the growth of the plasma temperature and by a migration of TPD (or hybrid TPD/aSRS) to slightly lower densities (
$n_{e}\approx 0.244\,n_{c}$
). The maximum splitting of the peaks is compatible with TPD (or hybrid TPD/aSRS) driven at a temperature of
${\sim}3.5{-}4~\text{keV}$
, which is close to the value given by CHIC simulations at times before the laser peak. The instability is finally damped at times close to the laser peak or a few tens of picoseconds after it, depending on the shot.
At times comparable to the disappearance of the TPD peaks, the peak produced by convective BRS becomes visible. In some shots, as shown in Figure 7 left, absolute instabilities at
${\sim}n_{c}/4$
and convective BRS coexist for a few tens of picoseconds. Since Landau damping of TPD/aSRS EPW is here low (
$k_{e}\unicode[STIX]{x1D706}_{D}\approx 0.14$
), the data suggest that the instability is damped by laser pump depletion due to BRS growth at lower densities. In some shots, a corresponding red-shifted peak, produced by
$\unicode[STIX]{x1D714}_{0}+\unicode[STIX]{x1D714}_{e}$
coupling, is visible in streaked images; this peak is usually less intense than the blue one, as shown for example by the spectrum b in Figure 7. Time-resolved spectra show also that BRS is present during all the trailing part of the laser pulse, often in visible bursts, and persists at late times. As already discussed in Ref. [Reference Cristoforetti, Antonelli, Atzeni, Baffigi, Barbato, Batani, Boutoux, Colaitis, Dostal, Dudzak, Juha, Koester, Marocchino, Mancelli, Nicolai, Renner, Santos, Schiavi, Skoric, Smid, Straka and Gizzi30], this is made possible by the increase of the density scalelength of the plasma at late times, which compensates the fall of laser intensity.
Another interesting piece of information is that BRS is initially driven as convective instability at a lower plasma density, corresponding to the lower wavelength edge of the BRS spectrum in Figure 3, and successively moves to higher densities. This can be clearly observed in
$\#$
52810 and by comparing the blue-shifted peaks in spectra a and b in Figure 7. In the tail of the laser pulse BRS reaches the plasma region close to
$n_{c}/4$
and is finally damped.
Now that local conditions (density, time) where SRS and TPD are driven have been discussed, it is possible to inspect the relation between these instabilities and the experimental HE temperatures.
The energy of HE generated by BRS can be calculated by considering the phase velocity
$v_{ph}=\unicode[STIX]{x1D714}_{e}/k_{e}$
, where
$\unicode[STIX]{x1D714}_{e}$
and
$k_{e}$
are the energy and the momentum of the EPW at the density of interest. By taking a maximum BRS reflectivity
$\unicode[STIX]{x1D706}=2400{-}2450~\text{nm}$
, as given by experimental spectra, corresponding to BRS driven at densities
$0.17{-}0.18\,n_{c}$
, and a plasma temperature of
${\sim}4~\text{keV}$
, corresponding to the laser peak time, we obtain an HE energy of
${\approx}40~\text{keV}$
. This value is in very good agreement with the colder HE temperature values given by the experimental data and by CHIC simulations. It is worth noting that HE generated by SRSS at lower densities, estimated at
$n_{e}\sim 0.12\,n_{c}$
as given by the peak of the SRSS spectrum (red curve in Figure 3), are expected to have a lower temperature
${\approx}25~\text{keV}$
. This suggests that low-density SRSS has a weaker impact on LPI and HE generation with respect to high-density BRS.
An estimate of the energy of HE generated by absolute TPD (or hybrid TPD/aSRS) is more tricky and less reliable. By considering the phase velocity of EPWs retrieved by the half-harmonic spectra, we obtain HE temperature values higher than
$100~\text{keV}$
. However, it is well known that such an approach is usually not reliable for estimating HE energy, since the acceleration of electrons at
$n_{c}/4$
usually can occur in different stages[Reference Yan, Ren, Li, Maximov, Mori, Sheng and Tsung7]; that is, thermal electrons are initially trapped and accelerated at lower densities, and their energy is successively boosted by absolute TPD or hybrid TPD/aSRS modes driven near
$n_{c}/4$
. These values suggest, however, that the experimental hotter component of HE could be produced by absolute instabilities driven in the plasma region close to
$n_{c}/4$
.
7 PIC simulations
Kinetic simulations of LPI have been performed with the relativistic electromagnetic PIC code EPOCH[Reference Arber, Bennett, Brady, Lawrence-Douglas, Ramsay, Sircombe, Gillies, Evans, Schmitz and Bell45] in the planar 2D geometry. Absorbing boundary conditions have been applied for the electromagnetic fields leaving the simulation box, while the particles have been thermalized to provide the cold return current. The initial density profile has been taken from the hydrodynamic simulations with the code CHIC corresponding to the peak of the laser pulse on target (time of 0 in Figure 2). The simulation is covering the density region from 0.03
$n_{c}$
to
$n_{c}$
, and thus resonance absorption and absolute and convective parametric instabilities including filamentation instability, BRS, TPD, SBS and parametric decay are accounted for. The plasma density gradient in the transverse direction is neglected for the sake of simplicity, as its characteristic scale is much smaller than that of the longitudinal density gradient. The initial electron temperature is set to 4.3 keV in the simulation box, in agreement with the hydrodynamic simulation. The average ion model is used to describe the ion species in the plastic (CH) target with an effective charge
$Z=3.5$
and a mass of 6.5 times the proton mass, with ions having an initial temperature of 250 eV. Coulomb collisions are neglected, as collisional absorption is relatively weak in this range of plasma temperatures and densities.
The simulation box has dimensions of
$355\unicode[STIX]{x1D706}_{0}$
in the longitudinal direction and
$200\unicode[STIX]{x1D706}_{0}$
in the transverse direction, with 40 cells per laser wavelength (
$\unicode[STIX]{x1D706}_{0}$
). Each cell includes 25 particles of each species, with the weight varying according to the local plasma density. The laser pulse has a Gaussian spatial profile with an FWHM of
$100~\unicode[STIX]{x03BC}\text{m}$
and the electric field vector in the simulation plane (p-polarization). It is propagating along the density gradient (normal with respect to the initial target surface). The temporal profile has a 1 ps ramp followed by a constant intensity (9 ps) corresponding to the peak of the laser pulse.
The first five picoseconds of the interaction is significantly influenced by a fast increase in the laser intensity, much faster than in the experiment. Thus we present here the results for the quasi-stationary stage of interaction, corresponding to the time from 5 to 9 ps. The longitudinal profile of the electron energy flux allows one to localize spatial zones where the laser absorption takes place. The electrons propagating into the target behind the critical density are responsible for a transport of about 10% of the incident laser energy flux, which gives the overall collisionless absorption. This electron energy flux is dominated by HE with a distribution which can be best fitted by the sum of two exponential functions with temperatures of 49 and 85 keV. The absorption process takes place in three spatially separated regions. About 1.3% of laser energy is absorbed in a low-density plasma in front of the quarter critical density surface, with the absorption rate being almost constant in this region. This region includes also the region where SRSS is observed in the experiment; however, since SRSS is driven more favourably in the s-polarization plane, the current simulation is not able to quantify this instability. About the same energy fraction (1.3%) is absorbed in a narrow region extending to about
$10\unicode[STIX]{x1D706}_{0}$
down from the critical density. The remaining part of 7.6% is absorbed in a region extending to 20–30
$\unicode[STIX]{x1D706}_{0}$
around
$n_{c}/4$
. This region includes the range of densities where BRS and TPD are observed in the experiment. These numbers correspond to the maximum laser pulse intensity; therefore, the overall absorption into HE may be overestimated for two reasons: laser interaction at times before and after the laser peak may be less efficient in producing HE, and accounting for the third spatial dimension may be less favourable for HE production. Considering these factors, HE conversion efficiency obtained by PIC simulation may be consistent with the value observed in the experiment
$\unicode[STIX]{x1D716}_{HE}=5.3\%\pm 2\%$
.
Figure 8. Spectrum of backscattered light recorded in front of the target during the quasi-stationary stage of the interaction (5–9 ps). The frequency is normalized to the laser frequency
$\unicode[STIX]{x1D714}_{0}$
.
Figure 9. Distribution of the Poynting flux in the laser propagation direction (in units
$\text{W}\,\cdot \,\text{cm}^{-2}$
) averaged temporally over 3 ps during the quasi-steady stage of interaction and spatially over one laser wavelength. Red and blue colours represent therefore incident and backscattered light, respectively. The incident laser beam is propagating from the left and the black vertical lines show the position of the quarter critical and critical density surfaces. The black dashed line is shown to guide the eye for the opening angle of backward propagating light.
Analysis of the simulation results shows that the overall interaction process is dominated by the laser beam filamentation, followed by SBS and SRS (see Figure 9 later). TPD is observed only during the initial transient stage of the interaction, and it is then quickly suppressed and replaced by strong SRS in the filaments, which develop in this region. These parametric processes manifest themselves in the spectrum of backscattered light shown in Figure 8. It consists of a weakly shifted part near the laser frequency, a broad downshifted wing and narrow features at the three-halves, second and third harmonics, as can be seen in Figure 8. A strong peak near the laser frequency is due to SBS, which develops in filaments over the plasma density profile up to the quarter critical density (see also Figure 9). A broad low-frequency wing in Figure 8 shows a double-hump feature around 0.5
$\unicode[STIX]{x1D714}_{0}$
and extends to both higher and lower frequencies. The part of the spectrum to the right from 0.5
$\unicode[STIX]{x1D714}_{0}$
corresponds to SRS originating from plasma densities lower than the quarter critical density. The most intense part of the spectrum in the frequency range 0.5–0.7
$\unicode[STIX]{x1D714}_{0}$
corresponds to SRS daughter waves generated in plasma with densities extending from 0.25
$n_{c}$
to 0.08
$n_{c}$
. The left wing at frequencies below 0.5
$\unicode[STIX]{x1D714}_{0}$
may be due to the resonance transformation of SRS-driven plasma waves into electromagnetic waves on local density inhomogeneities produced by filamentation[Reference Liao, Li, Li, Su, Zheng, Liu, Wang, Hu, Yan, Dunn, Nilsen, Hunter, Liu, Wang, Chen, Ma, Lu, Jin, Kodama, Sheng and Zhang46]. The harmonics
$2\unicode[STIX]{x1D714}_{0}$
and
$3\unicode[STIX]{x1D714}_{0}$
come from interaction at the critical surface. The peak around 1.5
$\unicode[STIX]{x1D714}_{0}$
has also a two-hump structure. It is similar to the feature near 1.5
$\unicode[STIX]{x1D714}_{0}$
observed in the experiment (Figure 7), but as TPD was weak in the simulation, electron plasma waves at this stage of interaction are likely produced by SRS or by a secondary parametric decay of SRS-driven plasma waves. The red-shifted component at 1.45
$\unicode[STIX]{x1D714}_{0}$
, corresponding to the wavelength of 900 nm, can be attributed to Thomson scattering of the laser wave or SBS daughter wave on the electron plasma waves induced by SRS. This component was observed also in some experimental shots. A weaker blue-shifted component (1.55
$\unicode[STIX]{x1D714}_{0}$
) is due to the scattering of the second harmonic on electron plasma waves excited near
$n_{c}/4$
, and corresponds to the experimental BRS feature shown in Figure 7. All these spectral features observed in simulations are therefore qualitatively similar to the ones observed in the experiment during the trailing part of the laser pulse. The double-hump structure of the 3/2
$\unicode[STIX]{x1D714}_{0}$
emission measured in the raising part of the laser pulse and related to TPD could here not be simulated; plasma conditions considered in the simulation, in fact, correspond to the peak intensity, where convective BRS dominates. The overall energy balance in the simulation box is largely dominated by SBS, which is responsible for 60% of laser energy reflected through the front simulation box boundary; the fraction of energy reflected in the back focusing cone is
${\sim}30\%$
(that is, larger than the value measured in the experiment), which may be explained by a temporal dependence of SBS on the interaction time. The SRS part of the backscattered light accounts only for 3% of laser energy. This value is in good agreement with the experimental value
${\sim}0.6\%{-}4\%$
, but it is in contrast to both the experimental data (
$5.3\%\pm 2\%$
) and the numerical value of energy transferred to HE in the region where SRS is driven (
${\sim}7.6\%$
). This discrepancy indicates that there are secondary processes (for example, parametric decay instability or resonance absorption) able to damp and transform the energy of SRS scattered light waves into plasma waves on local density modulations before they reach the front box boundary. These processes are described in more detail in Ref. [Reference Gu, Klimo, Nicolai, Shekhanov, Weber and Tikhonchuk47]. About
$22\%$
of laser energy is leaving the simulation box through the lateral boundaries and the lateral energy flux of electrons accounts for less than
$1\%$
of laser energy.
For the sake of clarity, a summary of the amount of laser energy spent in different channels, including both experimental and numerical data, is reported in Table 1. It is worth remarking that PIC results simulate
${\sim}$
4 ps of interaction at the laser peak intensity. Moreover, collisions are not included in PIC simulations; therefore, all the energy values referring to PIC data should be renormalized, taking into account the extent of collisional absorption.
Table 1. Energy spent in different energy channels during the interaction. The * symbol indicates mechanisms which have been observed but not quantified
a Simulations do not include collisions. Therefore, these values should be rescaled for the presence of collisional absorption.
b The value includes the energy scattered through the front (60%) and lateral (22%) boundaries of the simulation box.
c The value includes the estimated amount of HE driven by TPD and SRS.
Distribution of the electromagnetic field intensity in the simulation box averaged over 3 ps during the quasi-steady phase of the interaction is plotted in Figure 9. The laser pulse is propagating from the left (front) boundary and two thick vertical black lines correspond to the positions of the quarter critical and critical density surfaces. It can be seen clearly that the central part is dominated by the forward propagating incident laser (red regions) and the lateral side is dominated by backscattered light (blue regions). Filamentation, with a transverse size of the order of a few microns, similar to the speckle size, is observed for both the incident laser light, beginning at densities around 0.08
$n_{c}$
, and the backward propagating light in all the backscattering cone. Here, filamentation is excited spontaneously by numerical noise rather than by spatial intensity modulations. However, since the laser power into the speckles significantly exceeds the critical power for ponderomotive filamentation, we do not expect that the description of this process is qualitatively affected by the accurate modelling of speckle intensity statistics. It can be seen that only a small portion of the laser light, around
${\sim}20\%$
of the pulse energy, can penetrate behind the quarter critical density surface. The light propagates in narrow filaments with a finite angle with respect to the direction of incidence, and thus the process of resonance absorption at critical density is also accounted for. On the other hand, this process cannot significantly contribute to the overall energy balance since only
${\sim}1\%{-}2\%$
of laser energy reaches the critical density surface. The light filaments in front of the quarter critical density surface with transverse size of a few microns are also clearly observed. The intensity of the light in these filaments can be locally an order of magnitude higher than the incident pulse intensity (not shown in the figure because of temporal averaging). As our simulation is performed in a 2D planar geometry, the intensity in filaments can be even higher in the real 3D geometry because of filamentation and self-focusing in the third dimension. The black dashed line included in Figure 9 is a guide for the eye showing the backscattering light cone. Its angle is
$23^{\circ }$
with respect to the target normal. Most of the scattered light in the simulation is enclosed in the cone with this opening angle.
8 Conclusions
In the present experiment, LPI of an infrared laser pulse with a multilayer target at shock ignition intensity was characterized in detail. According to hydrodynamic simulations, the plasma temperature reaches values in excess of 4 keV during the interaction. The combination of laser intensity
${\sim}10^{16}~\text{W}\,\cdot \,\text{cm}^{-2}$
and temperature
${\sim}4~\text{keV}$
makes this experiment interesting to understand the characteristics of parametric instabilities in the SI regime.
On one hand, the value of plasma temperature determines the density range where convective BRS is driven. When temperature increases, Landau damping of BRS daughter plasma waves pushes the instability towards denser regions. On the other hand, plasma temperature is expected to rule the balance between TPD and SRS, because the threshold of TPD strongly increases in hot plasmas, leading to the damping of the instability. In our experiment, the presence of EPWs in the proximity of
$n_{c}/4$
, probably due to TPD or hybrid TPD/aSRS, is observed at early times of interaction when the plasma temperature is still low, and successively is suppressed at times close to the laser peak, when the temperature reaches the maximum value. At a comparable time, experimental spectra show evidence of the convective BRS onset. However, since the BRS is driven at lower densities, and therefore could not compete with absolute TPD, it is possible that TPD at
$n_{c}/4$
is damped by laser pump depletion due to BRS growth at lower densities or in filaments. As expected, PIC simulation carried out at laser peak time shows that TPD rapidly damps and SRS becomes dominant.
We want also to emphasize that a joint observation of
$3/2\unicode[STIX]{x1D714}_{0}$
,
$5/2\unicode[STIX]{x1D714}_{0}$
and
$7/2\unicode[STIX]{x1D714}_{0}$
allowed the detection and characterization of TPD (or hybrid TPD/aSRS), BRS and SRSS, driven in different density regions of the plasma.
A meaningful result of the present work is also the measurement of SRSS, which was rarely experimentally observed. This was measured at an angle of
${\sim}50^{\circ }$
which, considering plasma refraction, corresponds to light scattered at angles of
$65^{\circ }{-}90^{\circ }$
. According to recent simulations[Reference Xiao, Liu, Zheng and He18], SRSS is expected to become important at SI laser intensities, leading to laser energy scattered at large angles and to laser pump depletion that can damp TPD and SRS driven in denser plasma regions.
The results of 2D PIC simulations performed in the relevant interaction conditions confirm the framework delineated by the measurements and contribute to shedding further light on LPI and collisionless absorption mechanisms. PIC results show that filamentation instability rules the transport and the absorption of the laser light, in agreement with thresholds of classical theory. Filamentation is driven in the underdense plasma, in front of and slightly beyond the
$n_{c}/4$
region, and results in local laser intensities up to an order of magnitude higher than the value of incident intensity. In this way, filamentation rules the onset of SBS and SRS. Collisionless absorption of laser light by SRS becomes comparable to or even stronger than collisional absorption, and is responsible for the generation of HE with a probable conversion efficiency of the order of several percent. Secondary processes, such as parametric decay and resonance absorption, result in the partial absorption of BRS scattered light, so that calorimetry of the BRS light exiting the plasma could result in an underestimation of the overall collisionless absorbed energy. Inverse resonance absorption of SRS-driven plasma waves, in turn, results in a broad spectral range of infrared scattered light extending to frequencies lower than 0.5
$\unicode[STIX]{x1D714}_{0}$
.
Finally, experimental data, CHIC hydrodynamic simulations and PIC kinetic simulations suggest the presence of two HE components: the lower energy one, with a temperature around 40 keV, generated by the damping of BRS waves, and the higher energy one, with a temperature of
${\sim}$
80–100 keV, probably generated by instabilities driven in the proximity of
$n_{c}/4$
.
Acknowledgements
We would like to acknowledge financial support from the LASERLAB-EUROPE Access to Research Infrastructure activity within the ECs seventh Framework Program. This work has been carried out within the framework of the EUROfusion Consortium and has received funding from the Euratom research and training programme 2014–2018 under grant agreement No. 633053. The views and opinions expressed herein do not necessarily reflect those of the European Commission. This work was partially supported by the project ELITAS (ELI Tools for Advanced Simulation) CZ.02.1.01/0.0/0.0/16_013/0001793 and HIFI (High Field Initiative, CZ.02.1.01/0.0/0.0/15_003/0000449), ADONIS (Advanced research using high-intensity laser produced photons and particles, CZ.02.1.01/0.0/0.0/16_019/0000789), and ELITAS (ELI Tools for Advanced Simulations, CZ.02.1.01/0.0/0.0/16_013/0001793), all from European Regional Development Fund. The Czech participants appreciate financial support from the Czech Ministry of Education, Youth and Sports within grants LTT17015, LM2015083, and CZ.02.1.01/0.0/0.0/16_013/0001552 (EF16_013/0001552). The work of JIHT RAS group was done in the frame of the state assignment of FASO of Russia (topic #01201357846). We acknowledge SciTech Precision and Rutherford Appleton Laboratory Target Fabrication Group for the supplied targets. Finally, we thank the technical staff of PALS for help in running the experiments.
Open access
