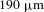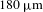1 Introduction
Recently, fiber lasers and amplifiers develop rapidly due to the demands of high energy and high peak power pulses in industries[Reference Hendow1] and scientific researches[Reference Richardson, Nilsson and Clarkson2]. The key technology in this progress is the development of larger mode field area fibers (especially very large mode field area (VLMA) fibers with mode-field diameters (MFDs) beyond ![]() $50~\unicode[STIX]{x03BC}\text{m}$) which is an effective way to increase the storage energy and mitigate intensity-related nonlinear effects[Reference Broderick, Offerhaus, Richardson, Sammut, Caplen and Dong3].
$50~\unicode[STIX]{x03BC}\text{m}$) which is an effective way to increase the storage energy and mitigate intensity-related nonlinear effects[Reference Broderick, Offerhaus, Richardson, Sammut, Caplen and Dong3].
Pulses with 26 mJ energy, 50 ns width and near diffraction limited beam quality have been reported with large pitch fiber in Q-switched fiber laser whose core diameter is ![]() $135~\unicode[STIX]{x03BC}\text{m}$[Reference Jansen, Stutzki, Liem, Jauregui, Limpert and Tunnermann4]. Using fiber with
$135~\unicode[STIX]{x03BC}\text{m}$[Reference Jansen, Stutzki, Liem, Jauregui, Limpert and Tunnermann4]. Using fiber with ![]() $200~\unicode[STIX]{x03BC}\text{m}$ core diameter in the final amplifier stage, pulses with
$200~\unicode[STIX]{x03BC}\text{m}$ core diameter in the final amplifier stage, pulses with ![]() ${>}82~\text{mJ}$ of pulse energy, 25 Hz repetition rate, and 500 ns pulse width are reported by using a cascade of four-stage Ytterbium-doped fiber amplifiers[Reference Cheng, Chang, Galvanauskas, Mamidipudi, Changkakoti and Gatchell5]. However, the maximum peak power for the nanosecond pulses in the above work is only around 3 MW[Reference Dinger, Grundmann, Hapke and Ruppik6, Reference Lin, Wang, Deng, Zhang, Xu, Zhu, Li and Huang7] which is mainly restricted by nonlinearity, e.g., stimulated Brillouin scattering (SBS), stimulated Raman scattering (SRS) and self-focusing (SF) in fiber.
${>}82~\text{mJ}$ of pulse energy, 25 Hz repetition rate, and 500 ns pulse width are reported by using a cascade of four-stage Ytterbium-doped fiber amplifiers[Reference Cheng, Chang, Galvanauskas, Mamidipudi, Changkakoti and Gatchell5]. However, the maximum peak power for the nanosecond pulses in the above work is only around 3 MW[Reference Dinger, Grundmann, Hapke and Ruppik6, Reference Lin, Wang, Deng, Zhang, Xu, Zhu, Li and Huang7] which is mainly restricted by nonlinearity, e.g., stimulated Brillouin scattering (SBS), stimulated Raman scattering (SRS) and self-focusing (SF) in fiber.
To improve the peak power further, we developed a new technology, i.e., utilizing broadband superluminescent pulsed light, such as the superluminescent diode light, super fluorescence or spontaneous emission light, as the seed source of the cascaded fiber amplifiers in as early as 2009 under the support of National High Technology Research and Development Program of China. We termed it as a superluminescent pulse amplification (SPA) technology. Broad bandwidth of wavelength helps to increase the SBS threshold in the VLMA fiber further, which makes higher peak power in fiber more achievable. Moreover, superluminescent light with nonlongitudinal mode and chaotic mode phase will suppress the modal interference, and make the light field intensity in the fiber more uniform, which mitigates the frequency modulation to amplitude modulation (FM-to-AM) effects, and scale up the peak power in the fiber.
In this paper, the limiting factors in achieving nanosecond pulses with high pulse energy and high peak power in fiber amplifiers are reviewed first. Then the influence of superluminescent pulses on the limitations of fiber amplifiers’ performance is analyzed. Moreover, a review of our experimental results for superluminescent pulses amplified in the fibers is made. Nanosecond pulses with peak power as high as 8 MW and pulse energy as much as 100 mJ are demonstrated. To improve the brightness of SPA light in the future work, we introduce our novel evaluation term and a more reasonable criterion which is denoted by a new parameter of brightness factor for active large mode area fiber designs. A core-doped active large pitch fiber with a core diameter of ![]() $190~\unicode[STIX]{x03BC}\text{m}$ and an MFD of
$190~\unicode[STIX]{x03BC}\text{m}$ and an MFD of ![]() $180~\unicode[STIX]{x03BC}\text{m}$ is designed by this method. The designed fiber allows near diffracted limited beam quality operation, and it can achieve 100 mJ pulse energy and 540 W average power by analyzing the mode coupling effects induced by heat.
$180~\unicode[STIX]{x03BC}\text{m}$ is designed by this method. The designed fiber allows near diffracted limited beam quality operation, and it can achieve 100 mJ pulse energy and 540 W average power by analyzing the mode coupling effects induced by heat.
2 Theoretical analysis for the limitations
2.1 Classical limitations for fiber amplifiers
Besides the extractable energy, the performance of fiber amplifiers is mainly limited to nonlinear effects and fiber damages.
Nonlinear effects
Even though most of the advantages of fiber amplifiers and lasers benefit from the fiber geometry, this geometry is also the source of its main limitations. Specifically, the long path lengths of the tightly confined light in the fiber core make the system more susceptible to nonlinear effects, even at modest powers. Various nonlinear effects can occur in optical fibers, but those that most degrade the performance of nanosecond fiber lasers are SBS (which usually dominates with narrowband signals), SRS (which usually dominates with broadband signals), self-phase modulation (SPM, which is important for short and ultrashort pulses) and SF (which sets the ultimate power limit).
The thresholds of SRS and SBS can be calculated as below[Reference Dawson, Messerly, Beach, Shverdin, Stappaerts, Sridharan, Pax, Heebner, Siders and Barty8]:
 $$\begin{eqnarray}\begin{array}{@{}l@{}}\displaystyle P_{SRS}=\frac{16\cdot K\cdot A_{\mathit{eff}}}{g_{R}\cdot L_{\mathit{eff}}},\\ \displaystyle P_{SBS}=\frac{21\cdot K\cdot A_{\mathit{eff}}}{g_{B}\cdot L_{\mathit{eff}}}\frac{\unicode[STIX]{x1D6E5}\unicode[STIX]{x1D708}_{B}+\unicode[STIX]{x1D6E5}\unicode[STIX]{x1D708}_{p}}{\unicode[STIX]{x1D6E5}\unicode[STIX]{x1D708}_{B}},\end{array}\end{eqnarray}$$
$$\begin{eqnarray}\begin{array}{@{}l@{}}\displaystyle P_{SRS}=\frac{16\cdot K\cdot A_{\mathit{eff}}}{g_{R}\cdot L_{\mathit{eff}}},\\ \displaystyle P_{SBS}=\frac{21\cdot K\cdot A_{\mathit{eff}}}{g_{B}\cdot L_{\mathit{eff}}}\frac{\unicode[STIX]{x1D6E5}\unicode[STIX]{x1D708}_{B}+\unicode[STIX]{x1D6E5}\unicode[STIX]{x1D708}_{p}}{\unicode[STIX]{x1D6E5}\unicode[STIX]{x1D708}_{B}},\end{array}\end{eqnarray}$$ where ![]() $g_{R}$ and
$g_{R}$ and ![]() $g_{B}$ are Raman and Brillouin gain coefficients, respectively,
$g_{B}$ are Raman and Brillouin gain coefficients, respectively, ![]() $A_{\mathit{eff}}$ is the effective mode area,
$A_{\mathit{eff}}$ is the effective mode area, ![]() $L_{\mathit{eff}}$ is the effective fiber length and
$L_{\mathit{eff}}$ is the effective fiber length and ![]() $K$ is a polarization-dependent coefficient which is taken as 1 when the light is line polarization and 2 when the polarization of light is random. The threshold for SBS also depends on the bandwidth of laser. In the equation,
$K$ is a polarization-dependent coefficient which is taken as 1 when the light is line polarization and 2 when the polarization of light is random. The threshold for SBS also depends on the bandwidth of laser. In the equation, ![]() $\unicode[STIX]{x1D6E5}\unicode[STIX]{x1D708}_{B}$ is the bandwidth of Brillouin gain spectrum,
$\unicode[STIX]{x1D6E5}\unicode[STIX]{x1D708}_{B}$ is the bandwidth of Brillouin gain spectrum, ![]() $\unicode[STIX]{x1D6E5}\unicode[STIX]{x1D708}_{p}$ is the bandwidth of laser.
$\unicode[STIX]{x1D6E5}\unicode[STIX]{x1D708}_{p}$ is the bandwidth of laser.
Different from the SBS and SRS effects which have sharp power thresholds, the SPM effect which results in spectral broadening has no threshold, and occurs in fiber amplifiers ubiquitously. The output spectrum induced by SPM can be calculated by solving the nonlinear Schrodinger (NLS) equations for coherent and incoherent pulses, respectively.
The ultimate limit for the fiber lasers is always SF[Reference Jauregui, Limpert and Tünnermann9]. Unlike other nonlinear effects, the SF limit is dependent only on the peak power of the beam; it does not depend on the peak intensity. This limit is ![]() ${\sim}4~\text{MW}$ for linearly polarized light and
${\sim}4~\text{MW}$ for linearly polarized light and ![]() ${\sim}6~\text{MW}$ for circularly polarized single-mode lasers at wavelengths around
${\sim}6~\text{MW}$ for circularly polarized single-mode lasers at wavelengths around ![]() $1~\unicode[STIX]{x03BC}\text{m}$.
$1~\unicode[STIX]{x03BC}\text{m}$.
Damage limits
Bulk damage and surface damage of fibers also limit the performance of fiber lasers and amplifiers. The study of Smith and Do[Reference Smith, Do, Hadley and Farrow10] shows that the bulk damage of fiber induced by nanosecond pulses occurs at a precise threshold irradiance. For multimode lasers, silica bulk damage occurs at a constant irradiance of ![]() $1.2~\text{kW}~\unicode[STIX]{x03BC}\text{m}^{-2}$, which means that the bulk damage limit could be as high as 36 MW for fibers with core diameter of
$1.2~\text{kW}~\unicode[STIX]{x03BC}\text{m}^{-2}$, which means that the bulk damage limit could be as high as 36 MW for fibers with core diameter of ![]() $200~\unicode[STIX]{x03BC}\text{m}$.
$200~\unicode[STIX]{x03BC}\text{m}$.
As for surface damage, in general, facets are more fragile and irregularities, roughness or dirt on the facet dramatically reduce the damage threshold. However, in the study of Smith and Do, it was shown that by proper polishing, the facet damage threshold can be made equal to the bulk damage. Moreover, the end cap spliced at the output of fibers can eliminate the surface damage for most fiber systems.
2.2 Theory analysis for the thresholds of superluminescent pulses amplified in fiber amplifiers
SF effects
With rapid development of high power pulsed fiber lasers and amplifiers, the pulse peak powers are getting increased. Megawatt level peak powers have been reported. With such high peak power, SF effect becomes the most important factor that limits the fiber amplifier output power. SF effect has been theoretically predicted and experimentally verified for over 50 years. Theory of SF effect gives the widely accepted power threshold for SF ![]() $P_{cr}=\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D706}^{2}/(4\unicode[STIX]{x1D70B}n_{0}n_{2})$. It is worth noting that this threshold formula is under the hypothesis that the propagated light is coherent. In our study[Reference Li, Zhang, Shen, Yan, Xin, Hao and Gong11], coherent property of light is taken into consideration by utilizing Wigner transform method in solving SF threshold of partially coherent light in LMA silica fibers. The formula of Equation (2) for SF threshold
$P_{cr}=\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D706}^{2}/(4\unicode[STIX]{x1D70B}n_{0}n_{2})$. It is worth noting that this threshold formula is under the hypothesis that the propagated light is coherent. In our study[Reference Li, Zhang, Shen, Yan, Xin, Hao and Gong11], coherent property of light is taken into consideration by utilizing Wigner transform method in solving SF threshold of partially coherent light in LMA silica fibers. The formula of Equation (2) for SF threshold ![]() $P_{cr}$ in MW unit applicable for both coherent and partially coherent light in LMA silica fibers is derived, which only depends on beam quality factor
$P_{cr}$ in MW unit applicable for both coherent and partially coherent light in LMA silica fibers is derived, which only depends on beam quality factor ![]() $\text{M}^{2}$ and bandwidth. It can be conveniently used to estimate SF threshold in experiment and design partially coherent high power fiber amplifiers.
$\text{M}^{2}$ and bandwidth. It can be conveniently used to estimate SF threshold in experiment and design partially coherent high power fiber amplifiers.
where ![]() $N=1+N_{\text{mod}}\unicode[STIX]{x1D70F}_{\text{mod}}L_{sf}/\unicode[STIX]{x1D70F}_{c}$,
$N=1+N_{\text{mod}}\unicode[STIX]{x1D70F}_{\text{mod}}L_{sf}/\unicode[STIX]{x1D70F}_{c}$, ![]() $L_{sf}$ is SF typical distance,
$L_{sf}$ is SF typical distance, ![]() $N_{\text{mod}}$ is fiber LP mode number,
$N_{\text{mod}}$ is fiber LP mode number, ![]() $\unicode[STIX]{x1D70F}_{\text{mod}}$ is mode dispersion factor,
$\unicode[STIX]{x1D70F}_{\text{mod}}$ is mode dispersion factor, ![]() $\unicode[STIX]{x1D70F}_{c}$ is coherent time and
$\unicode[STIX]{x1D70F}_{c}$ is coherent time and ![]() $N$ describes the temporal incoherence or induced spatial incoherence; larger
$N$ describes the temporal incoherence or induced spatial incoherence; larger ![]() $N$ implies poorer coherence
$N$ implies poorer coherence
For ![]() $N=1$, 2, 3, 5, 10, 20 and 100, the relations between SF power threshold
$N=1$, 2, 3, 5, 10, 20 and 100, the relations between SF power threshold ![]() $P_{cr}$ and beam quality factor
$P_{cr}$ and beam quality factor ![]() $\text{M}^{2}$ are displayed in Figure 1. All the curves are fitted by 2 order polynomial fittings with a confidence level of
$\text{M}^{2}$ are displayed in Figure 1. All the curves are fitted by 2 order polynomial fittings with a confidence level of ![]() $R>0.9952$. It is shown that SF threshold
$R>0.9952$. It is shown that SF threshold ![]() $P_{cr}$ is getting higher for larger
$P_{cr}$ is getting higher for larger ![]() $N$. It also can be noticed that when
$N$. It also can be noticed that when ![]() $\text{M}^{2}$ approaches 1,
$\text{M}^{2}$ approaches 1, ![]() $P_{cr}$ approaches the classical SF threshold of 4.2 MW for completely coherent light, regardless of the value of
$P_{cr}$ approaches the classical SF threshold of 4.2 MW for completely coherent light, regardless of the value of ![]() $N$.
$N$.

Figure 1. The dependence of the thresholds of SF on the beam quality.
SRS effects
SRS is an important limiting factor for achieving high peak power intensity in fiber amplifier systems. It was proposed to use partially coherent light to increase the SRS threshold significantly. In our study[Reference Li, Zhang, Shen, Yan, Hao and Gong12], the SRS threshold of partially coherent light in silica fibers is investigated by both experiments and theoretical analysis, which show that the SRS threshold is independent on light coherency when the bandwidth of the light is much narrower than 30 nm. We define the SRS suppression ratio ![]() $\times$ as power ratio of signal power to Raman power in dB which can be readily read out from measured spectrum. As shown in Figure 2, where solid circles represent theoretical predictions and solid triangles represent experimental data, the SRS critical power
$\times$ as power ratio of signal power to Raman power in dB which can be readily read out from measured spectrum. As shown in Figure 2, where solid circles represent theoretical predictions and solid triangles represent experimental data, the SRS critical power ![]() $P_{cr}$ decreases with increased SRS suppression ratio
$P_{cr}$ decreases with increased SRS suppression ratio ![]() $\times$ (dB). It can be seen that for SRS suppression ratio
$\times$ (dB). It can be seen that for SRS suppression ratio ![]() $\times$ greater than 15 dB, the experiment data agree with the theoretical predictions with maximum relative error of less than 2%. In another aspect, our prediction is failed for SRS suppression ratio
$\times$ greater than 15 dB, the experiment data agree with the theoretical predictions with maximum relative error of less than 2%. In another aspect, our prediction is failed for SRS suppression ratio ![]() $\times$ is less than 10 dB. However the prediction can be improved by taking into consideration the pump light depletion by SRS in our future work.
$\times$ is less than 10 dB. However the prediction can be improved by taking into consideration the pump light depletion by SRS in our future work.

Figure 2. The SRS thresholds in experiments and prediction.
Nevertheless, both the SRS experiment and theory results of incoherent light demonstrate that SRS has no relation to the phase status of the light. Therefore, partially coherent light does not help to break through the SRS limit. To understand the physical details, our theoretical model for SRS of partially coherent light in fibers is developed in Ref. [Reference Li, Zhang, Shen, Yan, Hao and Gong12].
SPM effects
For incoherent pulses, according to the Khinchin theorem, the output spectrum due to SPM is the Fourier transform of the first-order electric-field correlation function ![]() $K(z,\unicode[STIX]{x1D70F})$ of the output pulses, where
$K(z,\unicode[STIX]{x1D70F})$ of the output pulses, where ![]() $z$ is the position along the fiber,
$z$ is the position along the fiber, ![]() $\unicode[STIX]{x1D70F}$ is correlation time. Based on Manassah model[Reference Manassah13] and its improved form[Reference Kuznetsov, Podivilov and Babin14], the output spectrum for incoherent pulses can be written as
$\unicode[STIX]{x1D70F}$ is correlation time. Based on Manassah model[Reference Manassah13] and its improved form[Reference Kuznetsov, Podivilov and Babin14], the output spectrum for incoherent pulses can be written as
 $$\begin{eqnarray}\displaystyle & & \displaystyle I(z,\unicode[STIX]{x1D714})=\frac{1}{2\unicode[STIX]{x1D70B}}\int _{-\infty }^{+\infty }\,dTG(z,T)P(0,T)\nonumber\\ \displaystyle & & \displaystyle \quad \times \,\int _{-\infty }^{+\infty }d\unicode[STIX]{x1D70F}\frac{\unicode[STIX]{x1D705}(0,\unicode[STIX]{x1D70F})\text{e}^{\text{i}\unicode[STIX]{x1D714}^{\prime }\unicode[STIX]{x1D70F}}}{[1+(\unicode[STIX]{x1D6FE}P(0,T)L_{\mathit{eff}}(z,T))^{2}(1-|\unicode[STIX]{x1D705}(0,\unicode[STIX]{x1D70F})|^{2})]^{2}},\nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle I(z,\unicode[STIX]{x1D714})=\frac{1}{2\unicode[STIX]{x1D70B}}\int _{-\infty }^{+\infty }\,dTG(z,T)P(0,T)\nonumber\\ \displaystyle & & \displaystyle \quad \times \,\int _{-\infty }^{+\infty }d\unicode[STIX]{x1D70F}\frac{\unicode[STIX]{x1D705}(0,\unicode[STIX]{x1D70F})\text{e}^{\text{i}\unicode[STIX]{x1D714}^{\prime }\unicode[STIX]{x1D70F}}}{[1+(\unicode[STIX]{x1D6FE}P(0,T)L_{\mathit{eff}}(z,T))^{2}(1-|\unicode[STIX]{x1D705}(0,\unicode[STIX]{x1D70F})|^{2})]^{2}},\nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$ where ![]() $\unicode[STIX]{x1D6FE}$ is the nonlinear coefficient of the fiber,
$\unicode[STIX]{x1D6FE}$ is the nonlinear coefficient of the fiber, ![]() $T$ is the time measured in a frame of reference moving with the pulse at the group velocity
$T$ is the time measured in a frame of reference moving with the pulse at the group velocity ![]() $v_{g}$,
$v_{g}$, ![]() $G(z,T)$ is the power gain between the output pulse power
$G(z,T)$ is the power gain between the output pulse power ![]() $P(z,T)$ and the input pulse power
$P(z,T)$ and the input pulse power ![]() $P(0,T)$,
$P(0,T)$, ![]() $L_{\mathit{eff}}$ is the effective length of fiber,
$L_{\mathit{eff}}$ is the effective length of fiber, ![]() $\unicode[STIX]{x1D705}(0,\unicode[STIX]{x1D70F})=K(0,\unicode[STIX]{x1D70F})/P_{0}$ is the normalized correlation function of the input light and
$\unicode[STIX]{x1D705}(0,\unicode[STIX]{x1D70F})=K(0,\unicode[STIX]{x1D70F})/P_{0}$ is the normalized correlation function of the input light and ![]() $P_{0}$ is the peak power of input pulse.
$P_{0}$ is the peak power of input pulse.

Figure 3. The SPM-induced spectrum broadening at high peak power intensity: (a) the measured output pulse shape of the PCF fiber amplifier stage, and the predicted output pulse shape based on laser rate equations at different output pulse energy; (b) at pulse energy of 0.595 mJ, the RMS bandwidth of the output spectrum as a function of nonlinear coefficient; (c) the output spectrum at different peak power of output pulses; (d) the measured and calculated broadening factors as a function of peak power, and compared with the calculated results in small-signal model.

Figure 4. The experimental setup for cascaded fiber amplifiers in multimode operation.

Figure 5. The feasibility of 50 mJ pulse energy and 5 MW peak power delivered by the multistage fiber amplifier system.

Figure 6. The experimental setup for cascaded fiber amplifiers in single-mode operation.
However, in fiber amplifiers where high peak power is generated, we notice that the predicted results with Equation (3) are larger than the experimental results, as shown in the inset of Figure 3(a). The main reason might be that when the peak power intensity is larger than ![]() $1~\text{GW}~\text{cm}^{-2}$, the higher order nonlinear terms need to be considered in the NLS equation. In experiments[Reference Shen, Zhang, Hao, Li, Yan and Gong15], we notice that limited to the extraction ability of the experimental system, the peak power of pulses delivered by our amplifier lays in a relative narrow range (from 8 to 50 kW). So, we attempt to utilize a modified constant
$1~\text{GW}~\text{cm}^{-2}$, the higher order nonlinear terms need to be considered in the NLS equation. In experiments[Reference Shen, Zhang, Hao, Li, Yan and Gong15], we notice that limited to the extraction ability of the experimental system, the peak power of pulses delivered by our amplifier lays in a relative narrow range (from 8 to 50 kW). So, we attempt to utilize a modified constant ![]() $\unicode[STIX]{x1D6FE}^{\prime }$ to replace the nonlinear coefficient
$\unicode[STIX]{x1D6FE}^{\prime }$ to replace the nonlinear coefficient ![]() $\unicode[STIX]{x1D6FE}$ in our extended model based on cubic nonlinear term to predict the SPM-induced spectral broadening in our experimental condition. As shown in Figures 3(b)–(d), an excellent agreement between the experimental results especially at peak power of 25 and 50 kW and our easy approach is observed.
$\unicode[STIX]{x1D6FE}$ in our extended model based on cubic nonlinear term to predict the SPM-induced spectral broadening in our experimental condition. As shown in Figures 3(b)–(d), an excellent agreement between the experimental results especially at peak power of 25 and 50 kW and our easy approach is observed.
3 Experimental results for superluminescent pulse amplification in fiber amplifiers
We have reported the generation of nanosecond pulses with 55 mJ energy and 4.8 MW peak power in a multistage fiber amplifier system[Reference Zhang, Shen, Chen and Zheng16], which is seeded with 10 nm broadband pulses from a superluminescence diode (SLD). The experiment setup is shown in Figure 4. High energy and high peak power for nanosecond pulses are obtained simultaneously from fiber amplifier. Especially the peak power is at least two times the previous peak power for nanosecond pulses and approaches the SF critical power.
And at the same pump condition (250 mJ, 1 ms), without injection of seed pulses, the forward amplified spontaneous emission (ASE) energy is measured (0.56 mJ). With the seed pulses, the ASE energy must be lower than this value. So, the ASE ratio must be lower than 1% in the largest pulse energy we obtained.
The feasibility of 50 mJ pulse energy and 5 MW peak power delivered by the multistage fiber amplifier system is analyzed in Figure 5, including the extractable energy, bulk damage limit, SRS and SBS thresholds, and the classical self-focus limit.
It is noticeable that because of the multimode fibers used in the multistage fiber amplifier system, the beam quality is not good. The measured beam quality beta factor which refers to the value that the actual beam’s far-field divergence divided by the reference, i.e., the diffraction-limit beam’s far-field divergence is 11.
To explore the performance of superluminescent pulses in single-mode operation, we also report the construction of a cascaded fiber amplifier where a ![]() $40~\unicode[STIX]{x03BC}\text{m}$-core-diameter photonic crystal fiber is utilized in the main amplifier stage[Reference Shen, Zhang, Hao, Li, Li, Yan and Gong17]. Single-transverse-mode, linearly polarized, 7.5 ns pulses with 1.5 mJ energy, 123 kW peak power and 10 nm spectral bandwidth centered at 1062 nm are generated. The experimental setup is shown in Figure 6. To our knowledge, the pulse energy we obtain is the highest from
$40~\unicode[STIX]{x03BC}\text{m}$-core-diameter photonic crystal fiber is utilized in the main amplifier stage[Reference Shen, Zhang, Hao, Li, Li, Yan and Gong17]. Single-transverse-mode, linearly polarized, 7.5 ns pulses with 1.5 mJ energy, 123 kW peak power and 10 nm spectral bandwidth centered at 1062 nm are generated. The experimental setup is shown in Figure 6. To our knowledge, the pulse energy we obtain is the highest from ![]() $40~\unicode[STIX]{x03BC}\text{m}$-core-diameter photonic crystal fibers, and also the highest for long pulses (
$40~\unicode[STIX]{x03BC}\text{m}$-core-diameter photonic crystal fibers, and also the highest for long pulses (![]() ${>}1~\text{ns}$) with linear polarization and single transverse mode. The output pulse energy as a function of pump energy and the beam quality of the output pulses are shown in Figure 7.
${>}1~\text{ns}$) with linear polarization and single transverse mode. The output pulse energy as a function of pump energy and the beam quality of the output pulses are shown in Figure 7.

Figure 7. The output pulse energy as a function of pump energy and the beam quality of the output pulses.

Figure 8. End face of the large pitch fiber used and its several major modes.
4  $200~\unicode[STIX]{x03BC}\text{m}$ very large mode fiber design
$200~\unicode[STIX]{x03BC}\text{m}$ very large mode fiber design
The fiber output of high power, high energy and high beam quality at the same time is the future developing direction. To satisfy the developing requirement, the first step is designing and manufacturing the very large mode fiber. The fiber designs are usually guided in terms of transversal mode discrimination, i.e., different propagation losses, gains between modes. However, no standard of how much the discrimination should be is unified. The brightness of the fiber laser is a relative synthetical and representative performance parameter. To evaluate the brightness of superluminescent light, we present a novel evaluation term and a more reasonable criterion which is described by a new parameter of brightness factor for active large mode area fiber design[Reference Zhang, Chen, Hao, Yan and Gong18]. The brightness factor evaluation method is based on the transverse mode competition mechanism in fiber lasers and amplifiers. Brightness factor can be seen as a description of fiber general property since it can represent the output laser brightness of the fiber laser system and its ability to resist nonlinear effect.
With both desirable factors including high brightness and high nonlinear effect resistance taken into consideration, we propose a new parameter of brightness factor ![]() $\unicode[STIX]{x1D6E4}$ for the characterization of laser beams. It is defined as
$\unicode[STIX]{x1D6E4}$ for the characterization of laser beams. It is defined as
where ![]() $\unicode[STIX]{x1D702}$ is the power conversion efficiency of the pump laser to output signal,
$\unicode[STIX]{x1D702}$ is the power conversion efficiency of the pump laser to output signal, ![]() $d_{\mathit{eff}}$ is the diameter of the fundamental mode,
$d_{\mathit{eff}}$ is the diameter of the fundamental mode, ![]() $\text{M}^{2}$ denotes the beam quality,
$\text{M}^{2}$ denotes the beam quality, ![]() $\unicode[STIX]{x1D706}$ is the signal wavelength. Herein,
$\unicode[STIX]{x1D706}$ is the signal wavelength. Herein, ![]() $\unicode[STIX]{x1D702}/(\text{M}^{2}\unicode[STIX]{x1D706})^{2}$ denotes the output laser brightness in unit pump power. Brightness factor has instructive meaning in two aspects. (i) When the MFD of fundamental mode is fixed, the higher the output laser brightness in unit pump power is, the higher the pump conversion efficiency and the better focus intensity of the fiber laser will be. (ii) When the required laser brightness is fixed, the larger the MFD of FM is, the smaller the power density in the fiber will be, which can effectively resist nonlinear effect for high peak power pulses. Brightness factor can represent the output laser brightness of fiber laser system and its ability to resist nonlinear effect. Therefore, it can be seen as a description of fiber’s general properties.
$\unicode[STIX]{x1D702}/(\text{M}^{2}\unicode[STIX]{x1D706})^{2}$ denotes the output laser brightness in unit pump power. Brightness factor has instructive meaning in two aspects. (i) When the MFD of fundamental mode is fixed, the higher the output laser brightness in unit pump power is, the higher the pump conversion efficiency and the better focus intensity of the fiber laser will be. (ii) When the required laser brightness is fixed, the larger the MFD of FM is, the smaller the power density in the fiber will be, which can effectively resist nonlinear effect for high peak power pulses. Brightness factor can represent the output laser brightness of fiber laser system and its ability to resist nonlinear effect. Therefore, it can be seen as a description of fiber’s general properties.
A core-doped active large pitch fiber with a core diameter of ![]() $190~\unicode[STIX]{x03BC}\text{m}$ and an FM MFD of
$190~\unicode[STIX]{x03BC}\text{m}$ and an FM MFD of ![]() $180~\unicode[STIX]{x03BC}\text{m}$ is designed by this method[Reference Zhang, Chen, Ren, Yan and Gong19]. The endface of the designed fiber and its major modes is shown in Figure 8, which allows the effective single-mode operation by mode competition.
$180~\unicode[STIX]{x03BC}\text{m}$ is designed by this method[Reference Zhang, Chen, Ren, Yan and Gong19]. The endface of the designed fiber and its major modes is shown in Figure 8, which allows the effective single-mode operation by mode competition.
For the large pitch fiber with a core diameter of ![]() $190~\unicode[STIX]{x03BC}\text{m}$, we analyze the influence of mode coupling on the MFD and beam quality of output laser. The result shows that with the increase of the initial pump power, the fiber mode instability is enhanced, the MFD of output laser increases and the beam quality declines. The beam quality is the main factor restricting the promotion of average power for large mode area fiber. In the case of
$190~\unicode[STIX]{x03BC}\text{m}$, we analyze the influence of mode coupling on the MFD and beam quality of output laser. The result shows that with the increase of the initial pump power, the fiber mode instability is enhanced, the MFD of output laser increases and the beam quality declines. The beam quality is the main factor restricting the promotion of average power for large mode area fiber. In the case of ![]() $\text{M}^{2}<2$, the maximum average power reaches 540 W and the available pulse energy is
$\text{M}^{2}<2$, the maximum average power reaches 540 W and the available pulse energy is ![]() $80~\text{mJ}~\text{m}^{-1}$, which is suitable for high energy, high average power pulse amplifier with a repetition rate of more than 5 kHz.
$80~\text{mJ}~\text{m}^{-1}$, which is suitable for high energy, high average power pulse amplifier with a repetition rate of more than 5 kHz.
5 Conclusions
In this paper, to achieve nanosecond pulses with high pulse energy and high peak power in fiber amplifiers, we develop a new technology called SPA technology, i.e., utilizing broadband superluminescent pulsed light to seed the cascaded fiber amplifiers. The limiting factors in achieving nanosecond pulses with high pulse energy and high peak power in fiber amplifiers and the influence of superluminescent pulses on the limitations of fiber amplifiers’ performance is reviewed. Moreover, a review of our experimental results for superluminescent pulses amplified in the fibers is made. In multimode operation, for nanosecond pulses with peak power as high as 4.8 MW and pulse energy as much as 55 mJ are demonstrated. In single-mode operation, linearly polarized, 7.5 ns pulses with 1.5 mJ energy, 123 kW peak power are achieved. Moreover, we developed a new evaluation of the brightness of superluminescent light, and based on this criterion, a novel fiber with a core diameter of ![]() $190~\unicode[STIX]{x03BC}\text{m}$ and in single-mode operation is designed.
$190~\unicode[STIX]{x03BC}\text{m}$ and in single-mode operation is designed.
Acknowledgments
This research was supported by the National High Technology Research and Development Program of China, the National Natural Science Foundation of China (No. 61475081), and the State Key Laboratory of Tribology, Tsinghua University (No. SKLT2014B09).