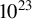1 Introduction
The research on inertial confinement fusion (ICF) started as early as 1960s[
Reference Atzeni and Meyer-ter Vehn
1
], where powerful laser beams should compress the deuterium–tritium (DT) fuel to density over several hundred times of the critical value (
![]() ${\sim} {10}^{21}$
cm–3) at a laser wavelength of 1 μm and heat the DT fuel up to around 10 keV. Because the non-relativistic laser is unable to propagate into the over-dense plasma due to the permittivity of plasma less than zero, various alternative schemes[
Reference Tabak, Norreys, Tikhonchuk and Tanaka
2
] are being pursued, where the intense laser pulses generate electron or ion beams and deposit energy indirectly to the compressed DT fuel, which intrinsically decreases the energy conversion efficiency from the laser to the plasma. However, it has been known for long time that if the electron gyrofrequency of the electromagnetic wave (called laser here) is higher than the laser frequency, that is,
${\sim} {10}^{21}$
cm–3) at a laser wavelength of 1 μm and heat the DT fuel up to around 10 keV. Because the non-relativistic laser is unable to propagate into the over-dense plasma due to the permittivity of plasma less than zero, various alternative schemes[
Reference Tabak, Norreys, Tikhonchuk and Tanaka
2
] are being pursued, where the intense laser pulses generate electron or ion beams and deposit energy indirectly to the compressed DT fuel, which intrinsically decreases the energy conversion efficiency from the laser to the plasma. However, it has been known for long time that if the electron gyrofrequency of the electromagnetic wave (called laser here) is higher than the laser frequency, that is,
![]() ${\omega}_{\mathrm{c}}= eB/{m}_{\mathrm{e}}c>{\omega}_{\mathrm{L}}$
, the right-handed circularly polarized (RHCP) non-relativistic laser could propagate into the over-dense magnetized plasma[
Reference Ginzburg
3
–
Reference Boyd and Sanderson
5
]. Such a phenomenon was first studied for the whistler phenomenon of radio waves (wavelength of
${\omega}_{\mathrm{c}}= eB/{m}_{\mathrm{e}}c>{\omega}_{\mathrm{L}}$
, the right-handed circularly polarized (RHCP) non-relativistic laser could propagate into the over-dense magnetized plasma[
Reference Ginzburg
3
–
Reference Boyd and Sanderson
5
]. Such a phenomenon was first studied for the whistler phenomenon of radio waves (wavelength of
![]() ${\lambda}_{\mathrm{L}}>{10}^4$
m) under the conditions of extremely low plasma density and extremely weak geomagnetic field (magnetic field of
${\lambda}_{\mathrm{L}}>{10}^4$
m) under the conditions of extremely low plasma density and extremely weak geomagnetic field (magnetic field of
![]() ${B}_0<{10}^{-4}$
T) in the 1960s[
Reference Chen
4
]. With the quick increase of the magnetic field strength in recent years, it is interesting to re-investigate the phenomenon of magnetic-induced plasma transparency, especially in the case of heating highly magnetized over-dense plasma with powerful (far-)infrared lasers propagating inside.
${B}_0<{10}^{-4}$
T) in the 1960s[
Reference Chen
4
]. With the quick increase of the magnetic field strength in recent years, it is interesting to re-investigate the phenomenon of magnetic-induced plasma transparency, especially in the case of heating highly magnetized over-dense plasma with powerful (far-)infrared lasers propagating inside.
The electron gyrofrequency being higher than the laser frequency is equivalent to the strength of the magnetic field being larger than a critical value,
![]() ${B}_0>{B}_{\mathrm{c}}=1.07\times {10}^4$
${B}_0>{B}_{\mathrm{c}}=1.07\times {10}^4$
![]() ${\lambda}_{\mathrm{L},\mu \mathrm{m}}^{-1}$
T[
Reference Li and Yu
6
,
Reference Li and Yu
7
]. Under such a condition, the permittivity of the magnetized plasma, in the case of RHCP lasers, is always above unity for any plasma density even above the over-critical value,
${\lambda}_{\mathrm{L},\mu \mathrm{m}}^{-1}$
T[
Reference Li and Yu
6
,
Reference Li and Yu
7
]. Under such a condition, the permittivity of the magnetized plasma, in the case of RHCP lasers, is always above unity for any plasma density even above the over-critical value,
![]() ${n}_{\mathrm{e}}>{n}_{\mathrm{c}}\approx 1.12\times {10}^{21}\ {\lambda}_{\mathrm{L},\mu \mathrm{m}}^{-2}$
${n}_{\mathrm{e}}>{n}_{\mathrm{c}}\approx 1.12\times {10}^{21}\ {\lambda}_{\mathrm{L},\mu \mathrm{m}}^{-2}$
![]() $\textrm{cm}^{-3}$
. For powerful Nd:YAG or
$\textrm{cm}^{-3}$
. For powerful Nd:YAG or
![]() ${\mathrm{CO}}_2$
lasers, which have wavelengths of around 1 or 10
${\mathrm{CO}}_2$
lasers, which have wavelengths of around 1 or 10
![]() $\mu \textrm{m}$
, the required strength of the magnetic field should be above
$\mu \textrm{m}$
, the required strength of the magnetic field should be above
![]() ${10}^4$
or
${10}^4$
or
![]() ${10}^3$
T, respectively. In recent years, researchers have discovered several ways to generate the macroscopic magnetic field with strength close to or higher than
${10}^3$
T, respectively. In recent years, researchers have discovered several ways to generate the macroscopic magnetic field with strength close to or higher than
![]() ${10}^3$
T in experiments. For example, in the scheme of a laser-driven capacitor-coil, a quasistationary magnetic field up to 600 T was generated when the Nd:glass laser with duration of 1 ns, pulse energy of 500 J and intensity of
${10}^3$
T in experiments. For example, in the scheme of a laser-driven capacitor-coil, a quasistationary magnetic field up to 600 T was generated when the Nd:glass laser with duration of 1 ns, pulse energy of 500 J and intensity of
![]() ${10}^{17}$
${10}^{17}$
![]() $\mathrm{W}\;{\mathrm{cm}}^{-2}$
was focused onto a copper coil with a coil diameter of 500
$\mathrm{W}\;{\mathrm{cm}}^{-2}$
was focused onto a copper coil with a coil diameter of 500
![]() $\mu \textrm{m}$
and wire cross-section of 50
$\mu \textrm{m}$
and wire cross-section of 50
![]() $\mu \textrm{m}$
[
Reference Santos, Bailly-Grandvaux, Giuffrida, Forestier-Colleoni, Fujioka, Zhang, Korneev, Bouillaud, Dorard, Batani, Chevrot, Cross, Crowston, Dubois, Gazave, Gregori, d’Humières, Hulin, Ishihara, Kojima, Loyez, Marquès, Morace, Nicolaï, Peyrusse, Poyé, Raffestin, Ribolzi, Roth, Schaumann, Serres, Tikhonchuk, Vacar and Woolsey
8
,
Reference Tikhonchuk, Bailly-Grandvaux, Santos and Poye
9
]. In the scheme of magnetic field compression by electromagnetic flux, the seed magnetic field of 3.2 T is enhanced to as high as 1200 T with input current energy of around 3 MJ[
Reference Nakamura, Ikeda, Sawabe, Matsuda and Takeyama
10
]. Such compression is also achieved using powerful OMEGA laser beams with energy of several kilojoules[
Reference Gotchev, Chang, Knauer, Meyerhofer, Polomarov, Frenje, Li, Manuel, Petrasso, Rygg, Séguin and Betti
11
], then the seed magnetic field is increased to the world-record 4000 T inside the cylindrically compressed deuterium plasma, where the averaged plasma density is around
$\mu \textrm{m}$
[
Reference Santos, Bailly-Grandvaux, Giuffrida, Forestier-Colleoni, Fujioka, Zhang, Korneev, Bouillaud, Dorard, Batani, Chevrot, Cross, Crowston, Dubois, Gazave, Gregori, d’Humières, Hulin, Ishihara, Kojima, Loyez, Marquès, Morace, Nicolaï, Peyrusse, Poyé, Raffestin, Ribolzi, Roth, Schaumann, Serres, Tikhonchuk, Vacar and Woolsey
8
,
Reference Tikhonchuk, Bailly-Grandvaux, Santos and Poye
9
]. In the scheme of magnetic field compression by electromagnetic flux, the seed magnetic field of 3.2 T is enhanced to as high as 1200 T with input current energy of around 3 MJ[
Reference Nakamura, Ikeda, Sawabe, Matsuda and Takeyama
10
]. Such compression is also achieved using powerful OMEGA laser beams with energy of several kilojoules[
Reference Gotchev, Chang, Knauer, Meyerhofer, Polomarov, Frenje, Li, Manuel, Petrasso, Rygg, Séguin and Betti
11
], then the seed magnetic field is increased to the world-record 4000 T inside the cylindrically compressed deuterium plasma, where the averaged plasma density is around
![]() ${10}^{23}$
${10}^{23}$
![]() $\textrm{cm}^{-3}$
, and the plasma temperature is around 3 keV at the cylindrical axis and around 0.5 keV at the radius of 15
$\textrm{cm}^{-3}$
, and the plasma temperature is around 3 keV at the cylindrical axis and around 0.5 keV at the radius of 15
![]() $\mu \textrm{m}$
. In theory, a longitudinal magnetic field even as high as
$\mu \textrm{m}$
. In theory, a longitudinal magnetic field even as high as
![]() ${10}^6$
T is obtained in the scheme of intense laser-driven microtube implosions, but with a microscopic dimension smaller than 1
${10}^6$
T is obtained in the scheme of intense laser-driven microtube implosions, but with a microscopic dimension smaller than 1
![]() $\mu \textrm{m}$
[
Reference Murakami, Honrubia, Weichman, Arefiev and Bulanov
12
].
$\mu \textrm{m}$
[
Reference Murakami, Honrubia, Weichman, Arefiev and Bulanov
12
].
The collisional interaction of RHCP lasers with highly magnetized over-dense plasma has been studied by the authors previously. In the first paper[ Reference Li and Yu 6 ], the propagation of an RHCP laser from vacuum into highly magnetized over-dense plasma is studied, where the plasma temperature is assumed to be constant. In the second paper[ Reference Li and Yu 7 ], the process of collisional heating is studied and the plasma is heated from 0.1 keV to around 1 keV, with other parameters of the laser, plasma and magnetic field being fixed. In this paper, the parameter dependence of this process will be studied both qualitatively and quantitatively, the scaling laws of plasma temperature, averaged heating depth and energy conversion efficiency will be obtained, and then plasma heating under more ‘practical’ conditions will be investigated.
2 Parameter dependence of plasma heating
The permittivity of magnetized collisional plasma, in the case of an RHCP wave, is given in the previous work[ Reference Li and Yu 6 , Reference Li and Yu 7 ]:
where
![]() $n={n}_{\mathrm{e}}/{n}_{\mathrm{c}}$
is the dimensionless plasma density with
$n={n}_{\mathrm{e}}/{n}_{\mathrm{c}}$
is the dimensionless plasma density with
![]() ${n}_{\mathrm{c}}\approx 1.12\times {10}^{21}{\lambda}_{\mathrm{L},\mu \mathrm{m}}^{-2}$
${n}_{\mathrm{c}}\approx 1.12\times {10}^{21}{\lambda}_{\mathrm{L},\mu \mathrm{m}}^{-2}$
![]() $\textrm{cm}^{-3}$
,
$\textrm{cm}^{-3}$
,
![]() $B={B}_0/{B}_{\mathrm{c}}$
is the dimensionless magnetic field with
$B={B}_0/{B}_{\mathrm{c}}$
is the dimensionless magnetic field with
![]() ${B}_{\mathrm{c}}=1.07\times {10}^4$
${B}_{\mathrm{c}}=1.07\times {10}^4$
![]() $\ {\lambda}_{\mathrm{L},\mu \mathrm{m}}^{-1}$
T and
$\ {\lambda}_{\mathrm{L},\mu \mathrm{m}}^{-1}$
T and
![]() $\nu ={\nu}_{\mathrm{ei}}/{\omega}_{\mathrm{L}}\approx 1.72\;(\ln\;\Lambda) Zn{\lambda}_{\mathrm{L}}^{-1}{T}_{\mathrm{eV}}^{-3/2}$
is the dimensionless electron–ion collision rate[
Reference Kruer
13
], with
$\nu ={\nu}_{\mathrm{ei}}/{\omega}_{\mathrm{L}}\approx 1.72\;(\ln\;\Lambda) Zn{\lambda}_{\mathrm{L}}^{-1}{T}_{\mathrm{eV}}^{-3/2}$
is the dimensionless electron–ion collision rate[
Reference Kruer
13
], with
![]() ${\omega}_{\mathrm{L}}$
being the angular frequency of the laser, Z is the number of free electrons per atom,
${\omega}_{\mathrm{L}}$
being the angular frequency of the laser, Z is the number of free electrons per atom,
![]() ${T}_{\mathrm{eV}}$
is the plasma temperature in unit of electron-volts,
${T}_{\mathrm{eV}}$
is the plasma temperature in unit of electron-volts,
![]() ${\lambda}_{\mathrm{L}}$
is the wavelength of the laser in unit of micrometres and
${\lambda}_{\mathrm{L}}$
is the wavelength of the laser in unit of micrometres and
![]() $\mathit{\ln}\Lambda$
is the Coulomb logarithm. The complex refractive index of plasma is
$\mathit{\ln}\Lambda$
is the Coulomb logarithm. The complex refractive index of plasma is
![]() $\tilde{n}={n}_{\mathrm{r}}+{in}_{\mathrm{i}}=\sqrt{\varepsilon }$
, and thus
$\tilde{n}={n}_{\mathrm{r}}+{in}_{\mathrm{i}}=\sqrt{\varepsilon }$
, and thus
![]() ${n}_{\mathrm{r}}$
is always positive in the case
${n}_{\mathrm{r}}$
is always positive in the case
![]() $B>1$
and the RHCP laser could propagate into plasma with any high density and deposit energy. The dependence of plasma heating on the parameters of the laser, plasma and magnetic field will be studied both qualitatively and quantitatively.
$B>1$
and the RHCP laser could propagate into plasma with any high density and deposit energy. The dependence of plasma heating on the parameters of the laser, plasma and magnetic field will be studied both qualitatively and quantitatively.
2.1 Qualitative investigation
In this paper, plasma or gas of deuterium and tritium will be studied, and thus Z is equal to 1 and
![]() $\mathit{\ln}\Lambda$
is assumed to be 1. The basic parameters in this paper are similar to previous work[
Reference Li and Yu
6
,
Reference Li and Yu
7
], that is,
$\mathit{\ln}\Lambda$
is assumed to be 1. The basic parameters in this paper are similar to previous work[
Reference Li and Yu
6
,
Reference Li and Yu
7
], that is,
![]() ${\lambda}_{\mathrm{L}}=1$
${\lambda}_{\mathrm{L}}=1$
![]() $\ \mu \textrm{m}$
,
$\ \mu \textrm{m}$
,
![]() ${n}_{\mathrm{e}}={10}^{23}$
${n}_{\mathrm{e}}={10}^{23}$
![]() $\ \textrm{cm}^{-3}$
(n = 100),
$\ \textrm{cm}^{-3}$
(n = 100),
![]() ${B}_0={10}^5$
T (B = 10), and the initial plasma temperature is
${B}_0={10}^5$
T (B = 10), and the initial plasma temperature is
![]() ${T}_0=$
0.1 keV, showing that the dimensionless collision rate is much less than unity, that is,
${T}_0=$
0.1 keV, showing that the dimensionless collision rate is much less than unity, that is,
![]() $\nu \ll 1$
. In this way, the dimensionless wave vector of the RHCP laser inside the plasma can be approximated as follows under conditions of
$\nu \ll 1$
. In this way, the dimensionless wave vector of the RHCP laser inside the plasma can be approximated as follows under conditions of
![]() $\nu \ll 1$
and
$\nu \ll 1$
and
![]() $B>1$
:
$B>1$
:
 $$\begin{align}k&=\sqrt{\varepsilon}={k}_{\mathrm{r}}+{ik}_{\mathrm{i}}\approx {\left(1+\frac{n}{B-1}\right)}^{1/2} \nonumber \\[5pt] &\quad +\frac{i}{2}\frac{n\nu}{{\left(B-1\right)}^2}{\left(\frac{1}{1+n/\left(B-1\right)}\right)}^{1/2},\end{align}$$
$$\begin{align}k&=\sqrt{\varepsilon}={k}_{\mathrm{r}}+{ik}_{\mathrm{i}}\approx {\left(1+\frac{n}{B-1}\right)}^{1/2} \nonumber \\[5pt] &\quad +\frac{i}{2}\frac{n\nu}{{\left(B-1\right)}^2}{\left(\frac{1}{1+n/\left(B-1\right)}\right)}^{1/2},\end{align}$$
where
![]() $k$
is the dimensionless wave vector of the RHCP laser in plasma, equalling the complex refractive index of plasma, that is,
$k$
is the dimensionless wave vector of the RHCP laser in plasma, equalling the complex refractive index of plasma, that is,
![]() $k=\tilde{n}$
and
$k=\tilde{n}$
and
![]() ${n}_{\mathrm{r}}+{in}_{\mathrm{i}}={k}_{\mathrm{r}}+{ik}_{\mathrm{i}}$
. The dimensionless wave vector is further approximated in the region of
${n}_{\mathrm{r}}+{in}_{\mathrm{i}}={k}_{\mathrm{r}}+{ik}_{\mathrm{i}}$
. The dimensionless wave vector is further approximated in the region of
![]() $n\gg B\gg 1$
with the effect of plasma temperature and laser wavelength:
$n\gg B\gg 1$
with the effect of plasma temperature and laser wavelength:
 $$\begin{align}{k}_{\mathrm{L}} &={k}_{\mathrm{r}}+{ik}_{\mathrm{i}}\approx {\left(\frac{n_1}{B_1}\cdot \frac{\lambda_{\mathrm{L}}}{\lambda_1}\right)}^{1/2} \nonumber \\[4pt] &\quad +i\cdot 0.86\;(\ln\;\Lambda) Z{\left(\frac{n_1}{B_1{T}_{\mathrm{eV}}}\right)}^{3/2}\frac{\lambda_{\mathrm{L}}^{1/2}}{\lambda_1^{3/2}},\end{align}$$
$$\begin{align}{k}_{\mathrm{L}} &={k}_{\mathrm{r}}+{ik}_{\mathrm{i}}\approx {\left(\frac{n_1}{B_1}\cdot \frac{\lambda_{\mathrm{L}}}{\lambda_1}\right)}^{1/2} \nonumber \\[4pt] &\quad +i\cdot 0.86\;(\ln\;\Lambda) Z{\left(\frac{n_1}{B_1{T}_{\mathrm{eV}}}\right)}^{3/2}\frac{\lambda_{\mathrm{L}}^{1/2}}{\lambda_1^{3/2}},\end{align}$$
where the parameters of the laser, plasma and magnetic field at a wavelength of 1
![]() $\mu \textrm{m}$
are denoted by subscript ‘1’ and
$\mu \textrm{m}$
are denoted by subscript ‘1’ and
![]() ${k}_{\mathrm{L}}$
is the dimensionless wave vector at wavelength
${k}_{\mathrm{L}}$
is the dimensionless wave vector at wavelength
![]() ${\lambda}_{\mathrm{L}}$
. It is also found that laser is blue-shifted inside the plasma since
${\lambda}_{\mathrm{L}}$
. It is also found that laser is blue-shifted inside the plasma since
![]() ${k}_{\mathrm{r}}$
is always above unity, and at the same time, the wavelength of laser inside the plasma decreases with higher plasma density and weaker magnetic field. The power transmission of the normally incident laser from vacuum into plasma and its approximation under the condition of
${k}_{\mathrm{r}}$
is always above unity, and at the same time, the wavelength of laser inside the plasma decreases with higher plasma density and weaker magnetic field. The power transmission of the normally incident laser from vacuum into plasma and its approximation under the condition of
![]() $n\gg B\gg 1$
are obtained based on the Fresnel equations:
$n\gg B\gg 1$
are obtained based on the Fresnel equations:
 $$\begin{align}\textrm{Trans}.=\frac{4{k}_{\mathrm{r}}}{{\left(1+{k}_{\mathrm{r}}\right)}^2}\approx 4{\left(\frac{B}{n}\right)}^{1/2}=4{\left(\frac{B_1}{n_1}\cdot \frac{\lambda_1}{\lambda_{\mathrm{L}}}\right)}^{1/2}.\end{align}$$
$$\begin{align}\textrm{Trans}.=\frac{4{k}_{\mathrm{r}}}{{\left(1+{k}_{\mathrm{r}}\right)}^2}\approx 4{\left(\frac{B}{n}\right)}^{1/2}=4{\left(\frac{B_1}{n_1}\cdot \frac{\lambda_1}{\lambda_{\mathrm{L}}}\right)}^{1/2}.\end{align}$$
In this way, the power transmission increases with lower plasma density, higher magnetic field and shorter laser wavelength, while it is not sensitive to plasma temperature, laser intensity and heating duration. For example,
![]() $\textrm{Trans}.\approx 0.3$
for
$\textrm{Trans}.\approx 0.3$
for
![]() $B=2$
and
$B=2$
and
![]() $n=100$
, while
$n=100$
, while
![]() $\textrm{Trans}.\approx 0.7$
for
$\textrm{Trans}.\approx 0.7$
for
![]() $B=10$
and
$B=10$
and
![]() $n=100$
, showing that
$n=100$
, showing that
![]() $B>3$
is required for high-power transmission. The attenuation length at wavelength
$B>3$
is required for high-power transmission. The attenuation length at wavelength
![]() ${\lambda}_{\mathrm{L}}$
in practical unit becomes
${\lambda}_{\mathrm{L}}$
in practical unit becomes
 $$\begin{align}{L}_{\alpha, {\lambda}_{\mathrm{L}}}={\left(2{k}_{\mathrm{L}}{k}_{\mathrm{i}}\right)}^{-1}\approx 0.1\;(\ln\;{\Lambda})^{-1}{Z}^{-1}{\lambda}_1^{3/2}{\lambda}_{\mathrm{L}}^{1/2}{\left(\frac{B_1{T}_{\mathrm{eV}}}{n_1}\right)}^{3/2}.\end{align}$$
$$\begin{align}{L}_{\alpha, {\lambda}_{\mathrm{L}}}={\left(2{k}_{\mathrm{L}}{k}_{\mathrm{i}}\right)}^{-1}\approx 0.1\;(\ln\;{\Lambda})^{-1}{Z}^{-1}{\lambda}_1^{3/2}{\lambda}_{\mathrm{L}}^{1/2}{\left(\frac{B_1{T}_{\mathrm{eV}}}{n_1}\right)}^{3/2}.\end{align}$$
In this way, the absorption length increases with lower plasma density, higher plasma temperature (thus laser intensity and duration), higher magnetic field and larger laser wavelength, which means that the RHCP laser prefers to deposit energy locally in the region of a weaker magnetic field, lower plasma temperature and higher plasma density. The increase of attenuation length with larger laser wavelength seems counter-intuitive, and thus it is further studied by varying the laser wavelength while keeping other parameters constant, for example,
![]() ${B}_0={10}^5$
T,
${B}_0={10}^5$
T,
![]() ${n}_{\mathrm{e}}={10}^{23}$
${n}_{\mathrm{e}}={10}^{23}$
![]() $\ \textrm{cm}^{-3}$
and
$\ \textrm{cm}^{-3}$
and
![]() $T=100$
eV. It is found that when
$T=100$
eV. It is found that when
![]() ${\lambda}_{\mathrm{L}}<0.1$
${\lambda}_{\mathrm{L}}<0.1$
![]() $\ \mu \textrm{m}$
(in the region of
$\ \mu \textrm{m}$
(in the region of
![]() $B<1$
), the attenuation length increases with shorter laser wavelength; however, when
$B<1$
), the attenuation length increases with shorter laser wavelength; however, when
![]() ${\lambda}_{\mathrm{L}}>0.1$
${\lambda}_{\mathrm{L}}>0.1$
![]() $\ \mu \textrm{m}$
(in the region of
$\ \mu \textrm{m}$
(in the region of
![]() $B>1$
), the attenuation length indeed increases with larger laser wavelength. In this way, in the region of
$B>1$
), the attenuation length indeed increases with larger laser wavelength. In this way, in the region of
![]() $B>1$
, a laser with larger wavelength propagates deeper in the highly magnetized over-dense plasma.
$B>1$
, a laser with larger wavelength propagates deeper in the highly magnetized over-dense plasma.
2.2 Quantitative investigation
The quantitative dependence is obtained by solving the equation of energy conservation between the laser and plasma as in the previous work[
Reference Li and Yu
7
], which is based on the processes of laser transmission and collisional absorption. The dimensionless potential vector of an incident planar RHCP laser propagating in vacuum is expressed as
![]() $\boldsymbol{a}={a}_0{e}^{iz-t}\left(\overrightarrow{x}+i\overrightarrow{y}\right)$
, where
$\boldsymbol{a}={a}_0{e}^{iz-t}\left(\overrightarrow{x}+i\overrightarrow{y}\right)$
, where
![]() $t={\omega}_{\mathrm{L}}{t}_0$
is the dimensionless time,
$t={\omega}_{\mathrm{L}}{t}_0$
is the dimensionless time,
![]() $z={k}_{\mathrm{L}}{z}_0$
is the dimensionless space and
$z={k}_{\mathrm{L}}{z}_0$
is the dimensionless space and
![]() ${I}_{\mathrm{L}}{\lambda}_{\mathrm{L},\mu \mathrm{m}}^2\approx 1.37\times {10}^{18}{a}_0^2$
${I}_{\mathrm{L}}{\lambda}_{\mathrm{L},\mu \mathrm{m}}^2\approx 1.37\times {10}^{18}{a}_0^2$
![]() $\ \textrm{W cm}^{-2}$
with
$\ \textrm{W cm}^{-2}$
with
![]() ${a}_0\approx 0.01$
for
${a}_0\approx 0.01$
for
![]() ${I}_{\mathrm{L}}={10}^{14}$
${I}_{\mathrm{L}}={10}^{14}$
![]() $\ \textrm{W cm}^{-2}$
and
$\ \textrm{W cm}^{-2}$
and
![]() ${\lambda}_{\mathrm{L}}=1$
${\lambda}_{\mathrm{L}}=1$
![]() $\ \mu \textrm{m}$
. For a normally incident laser, the dimensionless potential vector of the laser in plasma becomes
$\ \mu \textrm{m}$
. For a normally incident laser, the dimensionless potential vector of the laser in plasma becomes
where
![]() $k$
is the dimensionless wave vector in Equation (2) and
$k$
is the dimensionless wave vector in Equation (2) and
![]() $t=2/\left(1+k\right)$
is the transmission coefficient for the potential vector of the laser from vacuum to plasma. In the process of collisional interaction, the transverse velocity of electron driven by the RHCP laser in the magnetized plasma is as follows:
$t=2/\left(1+k\right)$
is the transmission coefficient for the potential vector of the laser from vacuum to plasma. In the process of collisional interaction, the transverse velocity of electron driven by the RHCP laser in the magnetized plasma is as follows:
Thus, the rate of laser absorption in plasma is
![]() $\nabla \cdot {\boldsymbol{S}}_{\mathrm{t}}={\partial}_{\mathrm{z}}\left({a}_1{a}_1^{\ast}\right)$
, and the rate of plasma heating by transverse electron current is the imaginary part of
$\nabla \cdot {\boldsymbol{S}}_{\mathrm{t}}={\partial}_{\mathrm{z}}\left({a}_1{a}_1^{\ast}\right)$
, and the rate of plasma heating by transverse electron current is the imaginary part of
![]() $-{\boldsymbol{J}}_{\mathrm{t}}\cdot {\boldsymbol{E}}_{\mathrm{t}}=-{nu}_{\mathrm{t}}\cdot {a}_1$
. The equation of plasma heating is thus obtained based on energy conservation between the laser and plasma:
$-{\boldsymbol{J}}_{\mathrm{t}}\cdot {\boldsymbol{E}}_{\mathrm{t}}=-{nu}_{\mathrm{t}}\cdot {a}_1$
. The equation of plasma heating is thus obtained based on energy conservation between the laser and plasma:
where
![]() ${w}_{\mathrm{L}}=\left(1+\mathit{\operatorname{Re}}\left(\varepsilon \right)\right){a}^2/2$
is the dimensionless energy density of the laser propagating inside plasma and
${w}_{\mathrm{L}}=\left(1+\mathit{\operatorname{Re}}\left(\varepsilon \right)\right){a}^2/2$
is the dimensionless energy density of the laser propagating inside plasma and
![]() ${w}_{\mathrm{P}}$
is the dimensionless energy density of plasma. In this paper, only the ideal gas-like plasma will be studied, requiring the plasma temperature to be much higher than the Fermi temperature,
${w}_{\mathrm{P}}$
is the dimensionless energy density of plasma. In this paper, only the ideal gas-like plasma will be studied, requiring the plasma temperature to be much higher than the Fermi temperature,
![]() ${T}_{\mathrm{eV}}>{\varepsilon}_{\mathrm{F}}\approx 7.9\ {n}_{23}^{2/3}$
eV. In this case, the dimensionless energy density of plasma is expressed as
${T}_{\mathrm{eV}}>{\varepsilon}_{\mathrm{F}}\approx 7.9\ {n}_{23}^{2/3}$
eV. In this case, the dimensionless energy density of plasma is expressed as
![]() ${w}_{\mathrm{P}}=3 nT$
[
Reference Drake
14
], with
${w}_{\mathrm{P}}=3 nT$
[
Reference Drake
14
], with
![]() $T={T}_{\mathrm{eV}}/{m}_{\mathrm{e}}{c}^2$
being the dimensionless plasma temperature. It should be noted that the energy loss of cyclotron emission is not taken into account here, and thus this equation is valid only when the strength of the magnetic field is much smaller than
$T={T}_{\mathrm{eV}}/{m}_{\mathrm{e}}{c}^2$
being the dimensionless plasma temperature. It should be noted that the energy loss of cyclotron emission is not taken into account here, and thus this equation is valid only when the strength of the magnetic field is much smaller than
![]() ${10}^5$
T, which will be explained later in this paper.
${10}^5$
T, which will be explained later in this paper.
Equation (8) is solved with the plasma temperature shown as the two identical black curves in Figures 1(a) and 1(b) with the set of basic parameters
![]() ${\tau}_{\mathrm{L}}=1$
ns,
${\tau}_{\mathrm{L}}=1$
ns,
![]() ${\lambda}_{\mathrm{L}}=1$
${\lambda}_{\mathrm{L}}=1$
![]() $\ \mu \textrm{m}$
,
$\ \mu \textrm{m}$
,
![]() ${a}_0=0.01$
,
${a}_0=0.01$
,
![]() $n=100$
,
$n=100$
,
![]() ${T}_0=100$
eV and
${T}_0=100$
eV and
![]() $B=10$
, which could be translated into practical units as
$B=10$
, which could be translated into practical units as
![]() ${I}_{\mathrm{L}}\approx {10}^{14}$
${I}_{\mathrm{L}}\approx {10}^{14}$
![]() $\ \mathrm{W}/{\mathrm{cm}}^2$
,
$\ \mathrm{W}/{\mathrm{cm}}^2$
,
![]() ${n}_{\mathrm{e}}\approx {10}^{23}$
${n}_{\mathrm{e}}\approx {10}^{23}$
![]() $\ \textrm{cm}^{-3}$
and
$\ \textrm{cm}^{-3}$
and
![]() ${B}_0\approx {10}^5$
T. When only one of above parameters is changed, the modified plasma temperature is shown as the colourful curves in Figures 1(a) and 1(b). It should be noted that the solid red curve in Figure 1(a) is shown at 10 ns while all others are at 1 ns. In this way, the dependences of plasma temperature at the vacuum–plasma boundary and averaged heating depth (attenuation length) on the parameters of the laser, plasma and magnetic field are obtained and are listed in Table 1, where the upper arrow means ‘increase with’, down arrow means ‘decrease with’ and the right arrow means ‘not sensitive to’. The dependence of power transmission is also calculated based on Equation (8) and is given in Table 1, which is not sensitive to an initial temperature above 100 eV because the dimensionless collisional rate is already much smaller than 1 for temperatures above 100 eV. The tendencies are same for the qualitative results.
${B}_0\approx {10}^5$
T. When only one of above parameters is changed, the modified plasma temperature is shown as the colourful curves in Figures 1(a) and 1(b). It should be noted that the solid red curve in Figure 1(a) is shown at 10 ns while all others are at 1 ns. In this way, the dependences of plasma temperature at the vacuum–plasma boundary and averaged heating depth (attenuation length) on the parameters of the laser, plasma and magnetic field are obtained and are listed in Table 1, where the upper arrow means ‘increase with’, down arrow means ‘decrease with’ and the right arrow means ‘not sensitive to’. The dependence of power transmission is also calculated based on Equation (8) and is given in Table 1, which is not sensitive to an initial temperature above 100 eV because the dimensionless collisional rate is already much smaller than 1 for temperatures above 100 eV. The tendencies are same for the qualitative results.

Figure 1 The temperature of plasma versus laser propagation depth inside plasma for the incident planar flat-top RHCP laser with duration of 1 ns except for the red solid curve of 10 ns. Parameters of the two identical black curves in (a) and (b): laser wavelength of
![]() ${\lambda}_{\mathrm{L}}=1$
${\lambda}_{\mathrm{L}}=1$
![]() $\ \mu \textrm{m}$
, intensity of
$\ \mu \textrm{m}$
, intensity of
![]() ${I}_{\mathrm{L}}={10}^{14}$
${I}_{\mathrm{L}}={10}^{14}$
![]() $\ \mathrm{W}/{\mathrm{cm}}^2$
, duration of
$\ \mathrm{W}/{\mathrm{cm}}^2$
, duration of
![]() ${\tau}_{\mathrm{L}}=1$
ns, plasma density of
${\tau}_{\mathrm{L}}=1$
ns, plasma density of
![]() ${n}_{\mathrm{e}}={10}^{23}$
${n}_{\mathrm{e}}={10}^{23}$
![]() $\ \textrm{cm}^{-3}$
, initial plasma temperature of
$\ \textrm{cm}^{-3}$
, initial plasma temperature of
![]() ${T}_0=0.1$
keV and magnetic field of
${T}_0=0.1$
keV and magnetic field of
![]() ${B}_0={10}^5$
T. Each of the other six colourful curves has one of the above parameters being changed, that is, (a)
${B}_0={10}^5$
T. Each of the other six colourful curves has one of the above parameters being changed, that is, (a)
![]() ${\tau}_{\mathrm{L}}=10$
ns (red, solid),
${\tau}_{\mathrm{L}}=10$
ns (red, solid),
![]() ${n}_{\mathrm{e}}=2\times {10}^{23}$
${n}_{\mathrm{e}}=2\times {10}^{23}$
![]() $\ \textrm{cm}^{-3}$
(blue, solid),
$\ \textrm{cm}^{-3}$
(blue, solid),
![]() ${B}_0=2\times {10}^5$
T (green, solid) and
${B}_0=2\times {10}^5$
T (green, solid) and
![]() ${B}_0=0.5\times {10}^5$
T (orange, solid); (b)
${B}_0=0.5\times {10}^5$
T (orange, solid); (b)
![]() ${I}_{\mathrm{L}}={10}^{15}$
${I}_{\mathrm{L}}={10}^{15}$
![]() $\ \textrm{W}/\textrm{cm}^2$
(red, dotted),
$\ \textrm{W}/\textrm{cm}^2$
(red, dotted),
![]() ${T}_0=200$
eV (blue, dotted) and
${T}_0=200$
eV (blue, dotted) and
![]() ${\lambda}_{\mathrm{L}}=10$
${\lambda}_{\mathrm{L}}=10$
![]() $\ \mu \textrm{m}$
(green, dotted).
$\ \mu \textrm{m}$
(green, dotted).
Table 1 Power transmission of the laser (Trans.), increase of plasma temperature at the vacuum–plasma boundary (
![]() ${T}_{\mathrm{b}}-{T}_0$
), averaged heating depth in micrometres (
${T}_{\mathrm{b}}-{T}_0$
), averaged heating depth in micrometres (
![]() ${d}_{\mu \mathrm{m}}$
) and energy conversion efficiency from laser to plasma (
${d}_{\mu \mathrm{m}}$
) and energy conversion efficiency from laser to plasma (
![]() ${\eta}_{\mathrm{L}\to \mathrm{P}}$
) versus various parameters, where
${\eta}_{\mathrm{L}\to \mathrm{P}}$
) versus various parameters, where
![]() $\uparrow$
means ‘increase with’,
$\uparrow$
means ‘increase with’,
![]() $\downarrow$
means ‘decrease with’ and
$\downarrow$
means ‘decrease with’ and
![]() $\to$
means ‘not sensitive to’.
$\to$
means ‘not sensitive to’.

2.3 Scaling laws
The scaling law can be obtained but only within the restricted region of parameters. For the set of basic parameters,
![]() ${\lambda}_{\mathrm{L}}=1$
${\lambda}_{\mathrm{L}}=1$
![]() $\ \mu \textrm{m}$
,
$\ \mu \textrm{m}$
,
![]() ${I}_{\mathrm{L}}={10}^{14}$
${I}_{\mathrm{L}}={10}^{14}$
![]() $\ \textrm{W cm}^{-2}$
,
$\ \textrm{W cm}^{-2}$
,
![]() ${n}_{\mathrm{e}}={10}^{23}$
${n}_{\mathrm{e}}={10}^{23}$
![]() $\ \textrm{cm}^{-3}$
and
$\ \textrm{cm}^{-3}$
and
![]() ${B}_0={10}^5$
T, the scaling law of the averaged heating depth scales versus the initial plasma temperature (
${B}_0={10}^5$
T, the scaling law of the averaged heating depth scales versus the initial plasma temperature (
![]() ${T}_0$
) is approximately to be
${T}_0$
) is approximately to be
while the boundary plasma temperature (
![]() ${T}_{\mathrm{b}}$
) is not sensitive to
${T}_{\mathrm{b}}$
) is not sensitive to
![]() ${T}_0$
. In this way, the RHCP laser could heat the hotter over-dense plasma in larger deepness. For fixed initial plasma temperature of
${T}_0$
. In this way, the RHCP laser could heat the hotter over-dense plasma in larger deepness. For fixed initial plasma temperature of
![]() ${T}_0=0.1$
keV, the scaling law of the boundary plasma temperature versus the parameters of the laser, plasma and magnetic field is as follows:
${T}_0=0.1$
keV, the scaling law of the boundary plasma temperature versus the parameters of the laser, plasma and magnetic field is as follows:
and the scaling law of averaged heating depth is as follows:
 $$\begin{align}{d}_{\mu \mathrm{m}} &\approx \left(15+7.7\log \left({I}_{14}\cdot {t}_{\mathrm{ns}}\right) +10\log \left({\lambda}_{\mu \mathrm{m}}\right)\right) \nonumber \\ &\quad \cdot {\left({B}_0/{10}^5\right)}^{1.37}\cdot {n}_{23}^{-1.53},\end{align}$$
$$\begin{align}{d}_{\mu \mathrm{m}} &\approx \left(15+7.7\log \left({I}_{14}\cdot {t}_{\mathrm{ns}}\right) +10\log \left({\lambda}_{\mu \mathrm{m}}\right)\right) \nonumber \\ &\quad \cdot {\left({B}_0/{10}^5\right)}^{1.37}\cdot {n}_{23}^{-1.53},\end{align}$$
where
![]() ${d}_{\mu \mathrm{m}}$
is the averaged heating depth in micrometres,
${d}_{\mu \mathrm{m}}$
is the averaged heating depth in micrometres,
![]() ${T}_{\mathrm{b},\mathrm{keV}}$
is the boundary temperature in keV,
${T}_{\mathrm{b},\mathrm{keV}}$
is the boundary temperature in keV,
![]() ${t}_{\mathrm{ns}}$
is the heating duration in nanoseconds,
${t}_{\mathrm{ns}}$
is the heating duration in nanoseconds,
![]() ${I}_{14}$
is the laser intensity in
${I}_{14}$
is the laser intensity in
![]() ${10}^{14}$
${10}^{14}$
![]() $\ \textrm{W cm}^{-2}$
,
$\ \textrm{W cm}^{-2}$
,
![]() ${\lambda}_{\mu \mathrm{m}}$
is the wavelength of the incident laser in micrometres,
${\lambda}_{\mu \mathrm{m}}$
is the wavelength of the incident laser in micrometres,
![]() ${B}_0$
is the strength of the magnetic field in teslas,
${B}_0$
is the strength of the magnetic field in teslas,
![]() ${n}_{23}$
is the plasma density in units of
${n}_{23}$
is the plasma density in units of
![]() ${10}^{23}$
${10}^{23}$
![]() $\ \textrm{cm}^{-3}$
. The above two scaling laws work under conditions of
$\ \textrm{cm}^{-3}$
. The above two scaling laws work under conditions of
![]() $B>3$
,
$B>3$
,
![]() $t>0.01$
ns,
$t>0.01$
ns,
![]() ${I}_{\mathrm{L}}>{10}^{12}$
${I}_{\mathrm{L}}>{10}^{12}$
![]() $\ \textrm{W cm}^{-2}$
and
$\ \textrm{W cm}^{-2}$
and
![]() $0.1<{\lambda}_{\mathrm{L}}<20$
$0.1<{\lambda}_{\mathrm{L}}<20$
![]() $\ \mu \textrm{m}$
. It is found that both the boundary temperature and heating depth increase with the radiant exposure (
$\ \mu \textrm{m}$
. It is found that both the boundary temperature and heating depth increase with the radiant exposure (
![]() $\mathrm{J}/{\mathrm{cm}}^2$
), the heating depth is most sensitive to the strength of the magnetic field and plasma density, and the boundary plasma temperature is most sensitive to the strength of the magnetic field and laser wavelength. In this way, a laser with larger wavelength should be applied to increase the heating depth, although with the sacrifice of decreased plasma temperature.
$\mathrm{J}/{\mathrm{cm}}^2$
), the heating depth is most sensitive to the strength of the magnetic field and plasma density, and the boundary plasma temperature is most sensitive to the strength of the magnetic field and laser wavelength. In this way, a laser with larger wavelength should be applied to increase the heating depth, although with the sacrifice of decreased plasma temperature.
The energy conversion efficiency from the laser to plasma is as follows:
 $$\begin{align}{\eta}_{\mathrm{L}\to \mathrm{P}}&=\frac{W_{\mathrm{p}}}{W_{\mathrm{L}}}=\left({\int}_0^{\mathrm{z}_{\mathrm{max}}}3{n}_{\mathrm{e}}\Delta T\textrm{d}z\right) \cdot {\left({I}_{\mathrm{L}}\tau \right)}^{-1} \nonumber \\ &\quad \approx 0.048{n}_{23}\frac{\left({T}_{\mathrm{b},\mathrm{keV}}-{T}_{0,\mathrm{keV}}\right){d}_{\mu \mathrm{m}}}{I_{14}{\tau}_{\mathrm{ns}}}.\end{align}$$
$$\begin{align}{\eta}_{\mathrm{L}\to \mathrm{P}}&=\frac{W_{\mathrm{p}}}{W_{\mathrm{L}}}=\left({\int}_0^{\mathrm{z}_{\mathrm{max}}}3{n}_{\mathrm{e}}\Delta T\textrm{d}z\right) \cdot {\left({I}_{\mathrm{L}}\tau \right)}^{-1} \nonumber \\ &\quad \approx 0.048{n}_{23}\frac{\left({T}_{\mathrm{b},\mathrm{keV}}-{T}_{0,\mathrm{keV}}\right){d}_{\mu \mathrm{m}}}{I_{14}{\tau}_{\mathrm{ns}}}.\end{align}$$
Inserting Equations (10) and (11), the energy conversion efficiency becomes
 $$\begin{align}{\eta}_{\mathrm{L}\to \mathrm{P}} &\approx 0.055\cdot {\left({B}_0/{10}^5\right)}^{0.82} \nonumber \\ &\quad \cdot \frac{15+3.33\log \left({I}_{14}{\tau}_{\mathrm{ns}}\right)+10\log \left({\lambda}_{\mu \mathrm{m}}\right)}{{\left({I}_{14}{\tau}_{\mathrm{ns}}\right)}^{0.6}{n}_{23}^{0.53}{\lambda}_{\mu \mathrm{m}}^{0.75}}.\end{align}$$
$$\begin{align}{\eta}_{\mathrm{L}\to \mathrm{P}} &\approx 0.055\cdot {\left({B}_0/{10}^5\right)}^{0.82} \nonumber \\ &\quad \cdot \frac{15+3.33\log \left({I}_{14}{\tau}_{\mathrm{ns}}\right)+10\log \left({\lambda}_{\mu \mathrm{m}}\right)}{{\left({I}_{14}{\tau}_{\mathrm{ns}}\right)}^{0.6}{n}_{23}^{0.53}{\lambda}_{\mu \mathrm{m}}^{0.75}}.\end{align}$$
In this way, the conversion efficiency increases with strength of the magnetic field, while it decreases with the radiation exposure of the laser, plasma density and wavelength of the laser, which is shown in Table 1. It should be noted again that since Equation (8) is valid when
![]() ${B}_0\ll {10}^5$
T, the above scaling laws also work only in this region.
${B}_0\ll {10}^5$
T, the above scaling laws also work only in this region.
3
Plasma heating with a powerful
 ${\mathrm{CO}}_2$
laser
${\mathrm{CO}}_2$
laser
Because the maximum available longitudinal macroscopic magnetic field is around
![]() $4\times {10}^3$
T[
Reference Gotchev, Chang, Knauer, Meyerhofer, Polomarov, Frenje, Li, Manuel, Petrasso, Rygg, Séguin and Betti
11
], a powerful laser with wavelength longer than 2.5
$4\times {10}^3$
T[
Reference Gotchev, Chang, Knauer, Meyerhofer, Polomarov, Frenje, Li, Manuel, Petrasso, Rygg, Séguin and Betti
11
], a powerful laser with wavelength longer than 2.5
![]() $\mu \textrm{m}$
must be found for ‘practical’ heating of plasma with density above
$\mu \textrm{m}$
must be found for ‘practical’ heating of plasma with density above
![]() ${10}^{21}$
${10}^{21}$
![]() $\ \textrm{cm}^{-3}$
, which is of interest in the field of laser–plasma-interaction. At the Brookhaven National Laboratory (BNL)[
Reference Pogorelsky, Babzien, Ben-Zvi, Skaritka and Polyanskiy
15
], a
$\ \textrm{cm}^{-3}$
, which is of interest in the field of laser–plasma-interaction. At the Brookhaven National Laboratory (BNL)[
Reference Pogorelsky, Babzien, Ben-Zvi, Skaritka and Polyanskiy
15
], a
![]() ${\mathrm{CO}}_2$
laser at the wavelength of 9.4
${\mathrm{CO}}_2$
laser at the wavelength of 9.4
![]() $\mu \textrm{m}$
is being built with pulse duration of 100 ps and pulse energy of around 70 J, which translates to a maximum laser intensity of around
$\mu \textrm{m}$
is being built with pulse duration of 100 ps and pulse energy of around 70 J, which translates to a maximum laser intensity of around
![]() $7\times {10}^{17}$
$7\times {10}^{17}$
![]() $\ \textrm{W cm}^{-2}$
at a focal spot diameter of 10
$\ \textrm{W cm}^{-2}$
at a focal spot diameter of 10
![]() $\mu \textrm{m}$
. To the best of the authors’ knowledge, this is the most powerful laser with a wavelength above 2.5
$\mu \textrm{m}$
. To the best of the authors’ knowledge, this is the most powerful laser with a wavelength above 2.5
![]() $\mu \textrm{m}$
right now.
$\mu \textrm{m}$
right now.
In this way, over-dense plasma heating by a
![]() ${\mathrm{CO}}_2$
laser at a wavelength of 10
${\mathrm{CO}}_2$
laser at a wavelength of 10
![]() $\mu \textrm{m}$
and magnetic fields of
$\mu \textrm{m}$
and magnetic fields of
![]() $4\times {10}^3$
and
$4\times {10}^3$
and
![]() ${10}^4$
T will be studied and compared with a
${10}^4$
T will be studied and compared with a
![]() $\mathrm{Nd}:\mathrm{YAG}$
laser, as shown in Figures 2(a) and 2(b), respectively. The dimensionless magnetic field is chosen to be
$\mathrm{Nd}:\mathrm{YAG}$
laser, as shown in Figures 2(a) and 2(b), respectively. The dimensionless magnetic field is chosen to be
![]() $B=10$
for both cases, which is translated into
$B=10$
for both cases, which is translated into
![]() ${B}_0={10}^4$
T for the
${B}_0={10}^4$
T for the
![]() ${\mathrm{CO}}_2$
laser and
${\mathrm{CO}}_2$
laser and
![]() ${B}_0={10}^5$
T for the
${B}_0={10}^5$
T for the
![]() $\mathrm{Nd}:\mathrm{YAG}$
laser. In both cases, the laser intensity is
$\mathrm{Nd}:\mathrm{YAG}$
laser. In both cases, the laser intensity is
![]() ${10}^{14}$
${10}^{14}$
![]() $\ \textrm{W cm}^{-2}$
, the duration is 1 ns and the initial plasma temperature is 0.1 keV. The averaged heating depth is simulated at various plasma densities, shown as red dots and fitted with a curve that has the same scaling law as Equation (11). It is found that plasma with lower density in the range of 1021–1022
$\ \textrm{W cm}^{-2}$
, the duration is 1 ns and the initial plasma temperature is 0.1 keV. The averaged heating depth is simulated at various plasma densities, shown as red dots and fitted with a curve that has the same scaling law as Equation (11). It is found that plasma with lower density in the range of 1021–1022
![]() $\ \textrm{cm}^{-3}$
could be heated up to 0.1–1 keV within depth 10–100
$\ \textrm{cm}^{-3}$
could be heated up to 0.1–1 keV within depth 10–100
![]() $\mu \textrm{m}$
. For the realized magnetized plasma with
$\mu \textrm{m}$
. For the realized magnetized plasma with
![]() ${B}_0=4\times {10}^3$
T,
${B}_0=4\times {10}^3$
T,
![]() ${n}_{\mathrm{e}}={10}^{23}$
${n}_{\mathrm{e}}={10}^{23}$
![]() $\ \textrm{cm}^{-3}$
and
$\ \textrm{cm}^{-3}$
and
![]() ${T}_0=1$
keV (assumed uniform)[
Reference Gotchev, Chang, Knauer, Meyerhofer, Polomarov, Frenje, Li, Manuel, Petrasso, Rygg, Séguin and Betti
11
], if the 1-ns
${T}_0=1$
keV (assumed uniform)[
Reference Gotchev, Chang, Knauer, Meyerhofer, Polomarov, Frenje, Li, Manuel, Petrasso, Rygg, Séguin and Betti
11
], if the 1-ns
![]() ${\mathrm{CO}}_2$
laser pulse is focused to an intensity of
${\mathrm{CO}}_2$
laser pulse is focused to an intensity of
![]() ${10}^{14}$
or
${10}^{14}$
or
![]() ${10}^{16}$
${10}^{16}$
![]() $\ \textrm{W cm}^{-2}$
, the plasma temperature will increase from 1 to 3 keV within several micrometres, as shown in Figure 3(a).
$\ \textrm{W cm}^{-2}$
, the plasma temperature will increase from 1 to 3 keV within several micrometres, as shown in Figure 3(a).

Figure 2 Heating of plasma with different densities by
![]() ${\mathrm{CO}}_2$
laser and Nd:YAG laser with
${\mathrm{CO}}_2$
laser and Nd:YAG laser with
![]() ${I}_{\mathrm{L}}={10}^{14}$
${I}_{\mathrm{L}}={10}^{14}$
![]() $\ \textrm{W cm}^{-2}$
,
$\ \textrm{W cm}^{-2}$
,
![]() ${\tau}_{\mathrm{L}}=1$
ns and
${\tau}_{\mathrm{L}}=1$
ns and
![]() ${T}_0=0.1$
keV. (a) Plasma temperature at the vacuum–plasma boundary versus plasma density:
${T}_0=0.1$
keV. (a) Plasma temperature at the vacuum–plasma boundary versus plasma density:
![]() ${\lambda}_{\mathrm{L}}=1$
${\lambda}_{\mathrm{L}}=1$
![]() $\ \mu \textrm{m}$
,
$\ \mu \textrm{m}$
,
![]() ${B}_0={10}^5$
T (black) and
${B}_0={10}^5$
T (black) and
![]() ${\lambda}_{\mathrm{L}}=10$
${\lambda}_{\mathrm{L}}=10$
![]() $\ \mu \textrm{m}$
,
$\ \mu \textrm{m}$
,
![]() ${B}_0={10}^4$
T (red). (b) Averaged heating depth versus plasma density:
${B}_0={10}^4$
T (red). (b) Averaged heating depth versus plasma density:
![]() ${\lambda}_{\mathrm{L}}=1$
${\lambda}_{\mathrm{L}}=1$
![]() $\ \mu \textrm{m}$
,
$\ \mu \textrm{m}$
,
![]() ${B}_0={10}^5$
T (black) and
${B}_0={10}^5$
T (black) and
![]() ${\lambda}_{\mathrm{L}}=10$
${\lambda}_{\mathrm{L}}=10$
![]() $\ \mu \textrm{m}$
,
$\ \mu \textrm{m}$
,
![]() ${B}_0={10}^4$
T (red), where the dots denote simulated depth and the lines denote the fitted curve.
${B}_0={10}^4$
T (red), where the dots denote simulated depth and the lines denote the fitted curve.

Figure 3 Heating of various plasmas by
![]() ${\mathrm{CO}}_2$
laser. (a) The uniform plasma is similar to the compressed plasma in Gotchev et al.
[
Reference Gotchev, Chang, Knauer, Meyerhofer, Polomarov, Frenje, Li, Manuel, Petrasso, Rygg, Séguin and Betti
11
], with
${\mathrm{CO}}_2$
laser. (a) The uniform plasma is similar to the compressed plasma in Gotchev et al.
[
Reference Gotchev, Chang, Knauer, Meyerhofer, Polomarov, Frenje, Li, Manuel, Petrasso, Rygg, Séguin and Betti
11
], with
![]() ${I}_{\mathrm{L}}= {10}^{14}$
${I}_{\mathrm{L}}= {10}^{14}$
![]() $\ \textrm{W cm}^{-2}$
(blue) or
$\ \textrm{W cm}^{-2}$
(blue) or
![]() ${I}_{\mathrm{L}}={10}^{16}$
${I}_{\mathrm{L}}={10}^{16}$
![]() $\ \textrm{W cm}^{-2}$
(orange),
$\ \textrm{W cm}^{-2}$
(orange),
![]() ${\tau}_{\mathrm{L}}=1$
ns,
${\tau}_{\mathrm{L}}=1$
ns,
![]() ${B}_0=4\times {10}^3$
T and
${B}_0=4\times {10}^3$
T and
![]() ${T}_0=1$
keV. (b) Sandwiched target with plasma densities of
${T}_0=1$
keV. (b) Sandwiched target with plasma densities of
![]() ${n}_{\mathrm{e}}={10}^{22}$
${n}_{\mathrm{e}}={10}^{22}$
![]() $\ \textrm{cm}^{-3}$
(
$\ \textrm{cm}^{-3}$
(
![]() $0<z<15\ \mu \textrm{m}$
and
$0<z<15\ \mu \textrm{m}$
and
![]() $z>18$
$z>18$
![]() $\ \mu \textrm{m}$
) and
$\ \mu \textrm{m}$
) and
![]() ${n}_{\mathrm{e}}={10}^{23}$
${n}_{\mathrm{e}}={10}^{23}$
![]() $\ \textrm{cm}^{-3}$
(blue) or
$\ \textrm{cm}^{-3}$
(blue) or
![]() ${n}_{\mathrm{e}}=5\times {10}^{23}$
${n}_{\mathrm{e}}=5\times {10}^{23}$
![]() $\ \textrm{cm}^{-3}$
(yellow) (
$\ \textrm{cm}^{-3}$
(yellow) (
![]() $15\ \mu\textrm{m} <z<18$
$15\ \mu\textrm{m} <z<18$
![]() $\ \mu \textrm{m}$
), where
$\ \mu \textrm{m}$
), where
![]() ${I}_{\mathrm{L}}={10}^{16}$
${I}_{\mathrm{L}}={10}^{16}$
![]() $\ \textrm{W cm}^{-2}$
,
$\ \textrm{W cm}^{-2}$
,
![]() ${\tau}_{\mathrm{L}}=1$
ns,
${\tau}_{\mathrm{L}}=1$
ns,
![]() ${T}_0=0.1$
keV and
${T}_0=0.1$
keV and
![]() ${B}_0= {10}^4$
T.
${B}_0= {10}^4$
T.
The properties of local heating or heating of non-uniform over-dense plasma are studied with sandwiched targets, as shown in Figure 3(b), where the plasma densities are
![]() ${10}^{22}$
${10}^{22}$
![]() $\ \textrm{cm}^{-3}$
in the first and third layers and
$\ \textrm{cm}^{-3}$
in the first and third layers and
![]() ${10}^{23}$
or
${10}^{23}$
or
![]() $5\times {10}^{23}$
$5\times {10}^{23}$
![]() $\ \textrm{cm}^{-3}$
in the second layer. It is found that the
$\ \textrm{cm}^{-3}$
in the second layer. It is found that the
![]() ${\mathrm{CO}}_2$
laser indeed deposits energy in the region of higher plasma density. The tendency of energy deposition in the region of lower temperature and weaker magnetic field is similar but not shown here.
${\mathrm{CO}}_2$
laser indeed deposits energy in the region of higher plasma density. The tendency of energy deposition in the region of lower temperature and weaker magnetic field is similar but not shown here.
4 Discussion and conclusions
The energy loss of cyclotron emission will be discussed here, especially for the plasma heating with a
![]() ${\mathrm{CO}}_2$
laser at a magnetic field of
${\mathrm{CO}}_2$
laser at a magnetic field of
![]() ${B}_0={10}^4$
T. In this case, the frequency of cyclotron emission is around
${B}_0={10}^4$
T. In this case, the frequency of cyclotron emission is around
![]() ${f}_{\mathrm{c}}\approx 2.8\times {10}^{10}B(T)= 2.8\times {10}^{14}$
Hz, smaller than the critical plasma frequency of
${f}_{\mathrm{c}}\approx 2.8\times {10}^{10}B(T)= 2.8\times {10}^{14}$
Hz, smaller than the critical plasma frequency of
![]() $2.8\times {10}^{15}$
Hz, and thus the plasma is opaque to the cyclotron emission. The energy of cyclotron emission per volume is approximated to be
$2.8\times {10}^{15}$
Hz, and thus the plasma is opaque to the cyclotron emission. The energy of cyclotron emission per volume is approximated to be
![]() $6.21{B}_{\mathrm{kT}}^2{n}_{23}{T}_{\mathrm{keV}}{\tau}_{\mathrm{ns}}\left(\mathrm{J}/{\mathrm{mm}}^3\right)$
[
Reference Huba
16
] while the energy density of plasma is
$6.21{B}_{\mathrm{kT}}^2{n}_{23}{T}_{\mathrm{keV}}{\tau}_{\mathrm{ns}}\left(\mathrm{J}/{\mathrm{mm}}^3\right)$
[
Reference Huba
16
] while the energy density of plasma is
![]() $4.8\times {10}^4{n}_{23}{T}_{\mathrm{keV}}$
$4.8\times {10}^4{n}_{23}{T}_{\mathrm{keV}}$
![]() $\ (\mathrm{J}/{\mathrm{mm}}^3)$
, and thus their ratio is approximately
$\ (\mathrm{J}/{\mathrm{mm}}^3)$
, and thus their ratio is approximately
![]() $1.3\times {10}^{-4}{B}_{\mathrm{kT}}^2{\tau}_{\mathrm{ns}}$
, which is as small as 0.013 in the case of
$1.3\times {10}^{-4}{B}_{\mathrm{kT}}^2{\tau}_{\mathrm{ns}}$
, which is as small as 0.013 in the case of
![]() ${B}_0={10}^4$
T and
${B}_0={10}^4$
T and
![]() ${\tau}_{\mathrm{L}}=1$
ns. In this way, the red curves in Figure 2, the curves in Figure 3 and the scaling laws are valid under condition of
${\tau}_{\mathrm{L}}=1$
ns. In this way, the red curves in Figure 2, the curves in Figure 3 and the scaling laws are valid under condition of
![]() ${B}_0\le {10}^4$
T. The contribution of cyclotron emission will be discussed in the future.
${B}_0\le {10}^4$
T. The contribution of cyclotron emission will be discussed in the future.
The energy density and pressure in the high-energy density plasma and magnetic field are very high here, for example, in the case of
![]() ${B}_0={10}^4$
T,
${B}_0={10}^4$
T,
![]() ${n}_{\mathrm{e}}={10}^{23}$
${n}_{\mathrm{e}}={10}^{23}$
![]() $\ \textrm{cm}^{-3}$
and
$\ \textrm{cm}^{-3}$
and
![]() ${T}_{\mathrm{e}}=1$
keV. The energy density and pressure of the magnetic field are approximately
${T}_{\mathrm{e}}=1$
keV. The energy density and pressure of the magnetic field are approximately
![]() ${w}_{\mathrm{B}}\approx 400{B}_{\mathrm{kT}}^2=4\times {10}^4$
${w}_{\mathrm{B}}\approx 400{B}_{\mathrm{kT}}^2=4\times {10}^4$
![]() $\ \mathrm{J}/{\mathrm{mm}}^{3}$
and
$\ \mathrm{J}/{\mathrm{mm}}^{3}$
and
![]() ${P}_{\mathrm{B}}\approx$
400 Mbar, and the energy density and pressure of plasma are
${P}_{\mathrm{B}}\approx$
400 Mbar, and the energy density and pressure of plasma are
![]() ${w}_{\mathrm{P}}\approx 4.8\times {10}^4{n}_{23}{T}_{\mathrm{keV}}=4.8\times {10}^4$
${w}_{\mathrm{P}}\approx 4.8\times {10}^4{n}_{23}{T}_{\mathrm{keV}}=4.8\times {10}^4$
![]() $\ \mathrm{J}/{\mathrm{mm}}^{3}$
and
$\ \mathrm{J}/{\mathrm{mm}}^{3}$
and
![]() ${P}_{\mathrm{P}}\approx$
480 Mbar. Because the ion sound velocity is approximately
${P}_{\mathrm{P}}\approx$
480 Mbar. Because the ion sound velocity is approximately
![]() ${c}_{\mathrm{s}}\approx 300{T}_{\mathrm{keV}}^{1/2}$
${c}_{\mathrm{s}}\approx 300{T}_{\mathrm{keV}}^{1/2}$
![]() $\mu \mathrm{m}/\mathrm{ns}$
[
Reference Huba
16
] in our case, the plasma would disassemble in a very short time, that is, a fraction of 1 ns, if not well confined. In order to confine the heated plasma, the strong
$\mu \mathrm{m}/\mathrm{ns}$
[
Reference Huba
16
] in our case, the plasma would disassemble in a very short time, that is, a fraction of 1 ns, if not well confined. In order to confine the heated plasma, the strong
![]() ${\mathrm{CO}}_2$
laser should be coupled to setups with high compression pressure, for example in the scheme of strong magnetic field generation[
Reference Gotchev, Chang, Knauer, Meyerhofer, Polomarov, Frenje, Li, Manuel, Petrasso, Rygg, Séguin and Betti
11
] or magnetized linear inertial fusion (MagLIF)[
Reference Sinars
17
,
Reference Yager-Elorriaga, Gomez, Ruiz, Slutz, Harvey-Thompson, Jennings, Knapp, Schmit, Weis, Awe, Chandler, Mangan, Myers, Fein, Galloway, Geissel, Glinsky, Hansen, Harding, Lamppa, Lewis, Rambo, Robertson, Savage, Shipley, Smith, Schwarz, Ampleford, Beckwith, Peterson, Porter, Rochau and Sinars
18
]. In MagLIF, the axial magnetic field is used to limit the thermal conduction from the hot plasma to the cold linear walls during the implosion, while in this paper the magnetic field will further assist in the increase of plasma temperature. Furthermore, although the energy densities of the magnetic field and plasma are similar here, the energy conversion efficiency in the generation of a strong magnetic field by laser compression (the energy of the compression lasers is around 10 kJ[
Reference Gotchev, Chang, Knauer, Meyerhofer, Polomarov, Frenje, Li, Manuel, Petrasso, Rygg, Séguin and Betti
11
]) is much less than by plasma heating. In this way, investigation of the efficient generation of a strong magnetic field is required to improve the total energy conversion efficiency.
${\mathrm{CO}}_2$
laser should be coupled to setups with high compression pressure, for example in the scheme of strong magnetic field generation[
Reference Gotchev, Chang, Knauer, Meyerhofer, Polomarov, Frenje, Li, Manuel, Petrasso, Rygg, Séguin and Betti
11
] or magnetized linear inertial fusion (MagLIF)[
Reference Sinars
17
,
Reference Yager-Elorriaga, Gomez, Ruiz, Slutz, Harvey-Thompson, Jennings, Knapp, Schmit, Weis, Awe, Chandler, Mangan, Myers, Fein, Galloway, Geissel, Glinsky, Hansen, Harding, Lamppa, Lewis, Rambo, Robertson, Savage, Shipley, Smith, Schwarz, Ampleford, Beckwith, Peterson, Porter, Rochau and Sinars
18
]. In MagLIF, the axial magnetic field is used to limit the thermal conduction from the hot plasma to the cold linear walls during the implosion, while in this paper the magnetic field will further assist in the increase of plasma temperature. Furthermore, although the energy densities of the magnetic field and plasma are similar here, the energy conversion efficiency in the generation of a strong magnetic field by laser compression (the energy of the compression lasers is around 10 kJ[
Reference Gotchev, Chang, Knauer, Meyerhofer, Polomarov, Frenje, Li, Manuel, Petrasso, Rygg, Séguin and Betti
11
]) is much less than by plasma heating. In this way, investigation of the efficient generation of a strong magnetic field is required to improve the total energy conversion efficiency.
Plasma heating with more ‘practical’ magnetic fields[
Reference Battesti, Beard, Boser, Bruyant, Budker, Crooker, Daw, Flambaum, Inada, Irastorza, Karbstein, Kim, Kozlov, Melhem, Phipps, Pugnat, Rikken, Rizzo, Schott, Semertzidis, Ten Kate and Zavattini
19
] of 100 and 10 T is discussed here. (1) When
![]() ${B}_0=$
100 T, lasers with wavelength larger than 100
${B}_0=$
100 T, lasers with wavelength larger than 100
![]() $\mu \textrm{m}$
are required to satisfy the condition of
$\mu \textrm{m}$
are required to satisfy the condition of
![]() $B>1$
in the heating plasma with density above
$B>1$
in the heating plasma with density above
![]() ${10}^{21}$
${10}^{21}$
![]() $\ \textrm{cm}^{-3}$
. Here, the heating of low-density foam at room temperature is studied as to the possibility for the generation of warm dense matter. For example, conditions of
$\ \textrm{cm}^{-3}$
. Here, the heating of low-density foam at room temperature is studied as to the possibility for the generation of warm dense matter. For example, conditions of
![]() ${n}_{\mathrm{e}}=2\times {10}^{21}$
${n}_{\mathrm{e}}=2\times {10}^{21}$
![]() $\ \textrm{cm}^{-3}$
,
$\ \textrm{cm}^{-3}$
,
![]() ${T}_0=0.026$
eV (300 K),
${T}_0=0.026$
eV (300 K),
![]() ${\lambda}_{\mathrm{L}}=300$
${\lambda}_{\mathrm{L}}=300$
![]() $\ \mu \textrm{m}$
(or 1 THz),
$\ \mu \textrm{m}$
(or 1 THz),
![]() ${I}_{\mathrm{L}}={10}^{10}$
${I}_{\mathrm{L}}={10}^{10}$
![]() $\ \textrm{W cm}^{-2}$
,
$\ \textrm{W cm}^{-2}$
,
![]() ${\tau}_{\mathrm{L}}\,{=}\,0.1$
ns and
${\tau}_{\mathrm{L}}\,{=}\,0.1$
ns and
![]() ${B}_0=100$
T are applied, which results in plasma temperature between 0.125 eV (Fermi energy) and 4.2 eV within a depth of around 15
${B}_0=100$
T are applied, which results in plasma temperature between 0.125 eV (Fermi energy) and 4.2 eV within a depth of around 15
![]() $\mu \textrm{m}$
. The energy of this terahertz pulse is 0.9 mJ for the beam diameter of 300
$\mu \textrm{m}$
. The energy of this terahertz pulse is 0.9 mJ for the beam diameter of 300
![]() $\mu \textrm{m}$
, while a terahertz pulse with energy of 0.9 mJ has been efficiently generated from an organic DSTMS (4-N,N-dimethylamino-4’-N’-methyl-stilbazolium 2,4,6-trimethylbenzenesulfonate) crystal by a short-pulsed laser[
Reference Vicario, Ovchinnikov, Ashitkov, Agranat, Fortov and Hauri
20
]. It must be noted that the initial temperature of 0.026 eV is below the Fermi energy, and thus the energy density of ‘plasma’ in Equation (8) should be modified, which requires further investigation. (2) When
$\mu \textrm{m}$
, while a terahertz pulse with energy of 0.9 mJ has been efficiently generated from an organic DSTMS (4-N,N-dimethylamino-4’-N’-methyl-stilbazolium 2,4,6-trimethylbenzenesulfonate) crystal by a short-pulsed laser[
Reference Vicario, Ovchinnikov, Ashitkov, Agranat, Fortov and Hauri
20
]. It must be noted that the initial temperature of 0.026 eV is below the Fermi energy, and thus the energy density of ‘plasma’ in Equation (8) should be modified, which requires further investigation. (2) When
![]() ${B}_0=$
10 T, lasers with a wavelength larger than 1000
${B}_0=$
10 T, lasers with a wavelength larger than 1000
![]() $\mu \textrm{m}$
are required to heat the over-dense plasma, but the heating depth, boundary plasma temperature and energy conversion efficiency become too small to be applicable, as shown in the scaling laws. It might find applications in heating plasma with density below
$\mu \textrm{m}$
are required to heat the over-dense plasma, but the heating depth, boundary plasma temperature and energy conversion efficiency become too small to be applicable, as shown in the scaling laws. It might find applications in heating plasma with density below
![]() ${10}^{21}$
${10}^{21}$
![]() $\ \textrm{cm}^{-3}$
but is still over-dense for the 1000-
$\ \textrm{cm}^{-3}$
but is still over-dense for the 1000-
![]() $\mu \textrm{m}$
‘laser’, such as in the scheme of magnetic fusion, but not in the scope of this paper. In addition, Equation (8) is still valid for both RHCP and left-handed circularly polarized (LHCP) lasers in the region of
$\mu \textrm{m}$
‘laser’, such as in the scheme of magnetic fusion, but not in the scope of this paper. In addition, Equation (8) is still valid for both RHCP and left-handed circularly polarized (LHCP) lasers in the region of
![]() $B<1$
and
$B<1$
and
![]() $n<1$
, and thus it could also be used in applications such as magnetic field measurement due to the Faraday effect or magnetic splitting of a short-pulse laser in plasma[
Reference Weng, Zhao, Sheng, Yu, Luan, Chen, Yu, Murakami, Mori and Zhang
21
] if the plasma heating by the probe laser is to be necessarily taken into account.
$n<1$
, and thus it could also be used in applications such as magnetic field measurement due to the Faraday effect or magnetic splitting of a short-pulse laser in plasma[
Reference Weng, Zhao, Sheng, Yu, Luan, Chen, Yu, Murakami, Mori and Zhang
21
] if the plasma heating by the probe laser is to be necessarily taken into account.
The analytical study in this paper has clarified the main properties of plasma heating but is still very preliminary. For example, collisional heating might not be the only process of laser–plasma interaction in the intensity range of 1014–1016 cm–2 for
![]() ${\mathrm{CO}}_2$
lasers and at this high plasma density level; thus, the simplified calculation here is used to explain the basic heating results due to the phenomenon of magnetically-induced transparency. The effect of a non-uniform magnetic field is not discussed here. For example, the magnetic profile with a strong field at the centre and a weak one at the edge[
Reference Gotchev, Chang, Knauer, Meyerhofer, Polomarov, Frenje, Li, Manuel, Petrasso, Rygg, Séguin and Betti
11
] will generate magnetized plasma with a refractive index as the negative lens, which will defocus the laser. In addition, non-uniform plasma with a higher density at the centre will work as a positive lens. These effects will be discussed in the future work. Furthermore, only a transverse mode laser is taken into account, while the longitudinal mode also exists in the over-dense magnetized plasma, which will also be discussed in the future.
${\mathrm{CO}}_2$
lasers and at this high plasma density level; thus, the simplified calculation here is used to explain the basic heating results due to the phenomenon of magnetically-induced transparency. The effect of a non-uniform magnetic field is not discussed here. For example, the magnetic profile with a strong field at the centre and a weak one at the edge[
Reference Gotchev, Chang, Knauer, Meyerhofer, Polomarov, Frenje, Li, Manuel, Petrasso, Rygg, Séguin and Betti
11
] will generate magnetized plasma with a refractive index as the negative lens, which will defocus the laser. In addition, non-uniform plasma with a higher density at the centre will work as a positive lens. These effects will be discussed in the future work. Furthermore, only a transverse mode laser is taken into account, while the longitudinal mode also exists in the over-dense magnetized plasma, which will also be discussed in the future.
In conclusion, the collisional heating of highly magnetized over-dense plasma by an RHCP laser is completely studied here with novel phenomena discovered, for example, the laser is blue-shifted in the over-dense plasma, the heating depth increases with larger wavelength in the region of
![]() $B>1$
and the laser deposits energy locally due to a higher density, lower temperature or weaker magnetic field. The scaling laws are obtained, and thus the dependence of plasma heating on the parameters of the laser, plasma and magnetic field is quantitatively clarified, and the scaling law could be applied in guiding possible applications in the future. Plasma heating with a nanosecond
$B>1$
and the laser deposits energy locally due to a higher density, lower temperature or weaker magnetic field. The scaling laws are obtained, and thus the dependence of plasma heating on the parameters of the laser, plasma and magnetic field is quantitatively clarified, and the scaling law could be applied in guiding possible applications in the future. Plasma heating with a nanosecond
![]() ${\mathrm{CO}}_2$
laser at the intensity of
${\mathrm{CO}}_2$
laser at the intensity of
![]() ${10}^{16}$
cm–2 and magnetic field of
${10}^{16}$
cm–2 and magnetic field of
![]() $4\times {10}^3$
T is studied, and if well confined, the DT plasma with density of
$4\times {10}^3$
T is studied, and if well confined, the DT plasma with density of
![]() ${10}^{23}$
${10}^{23}$
![]() $\ \textrm{cm}^{-3}$
and initial temperature of 1 keV could be heated to nearly 10 keV within around 10 μm.
$\ \textrm{cm}^{-3}$
and initial temperature of 1 keV could be heated to nearly 10 keV within around 10 μm.
Acknowledgements
The authors gratefully acknowledge the discussion with Professor Vladimir Tikhonchuk of Centre Lasers Intenses et Applications and University of Bordeaux and Prof. Xu Han of the National University of Defense Technology. This work was supported by the Start-up fund from Shantou University (No. NTF21003), the Science and Technology Fund of Guangdong Province (No. STKJ2021018) and the National Natural Science Foundation of China (NSFC) (No. 12075317).
Data availability
The data that support the findings of this study are available from the corresponding author upon reasonable request.