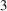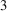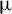1. Introduction
Laser plasma accelerators (LPAs) for protons have progressed to the point where various applications benefiting from the particular source characteristics are pursued as independent research fields[
Reference Albert, Couprie, Debus, Downer, Faure, Flacco, Gizzi, Grismayer, Huebl, Joshi, Labat, Leemans, Maier, Mangles, Mason, Mathieu, Muggli, Nishiuchi, Osterhoff, Rajeev, Schramm, Schreiber, Thomas, Vay, Vranic and Zeil1]. Ultra-high dose rate radiobiology was promoted as a key application for LPA protons early on[
Reference Wilks, Langdon, Cowan, Roth, Singh, Hatchett, Key, Pennington, Mackinnon and Snavely2]. LPA proton bunches, with up to
![]() ${10}^{13}$
protons per bunch, yield dose rates unreachable at clinical accelerators and can hence contribute to the current quest to investigate the radiobiological benefits of ultra-high dose rates[
Reference Esplen, Mendonca and Bazalova-Carter3]. Thanks to the now achievable reproducible multi-10 MeV kinetic energies on high repetition rate (
${10}^{13}$
protons per bunch, yield dose rates unreachable at clinical accelerators and can hence contribute to the current quest to investigate the radiobiological benefits of ultra-high dose rates[
Reference Esplen, Mendonca and Bazalova-Carter3]. Thanks to the now achievable reproducible multi-10 MeV kinetic energies on high repetition rate (
![]() $\sim$
Hz) laser systems, irradiation of mm-scale radiobiological samples is possible. Current radiobiological studies at LPA proton sources hence focus on small animal irradiations in a dose range from approximately 100 mGy to multi-10 Gy[
Reference Kroll, Brack, Bernert, Bock, Bodenstein, Brüchner, Cowan, Gaus, Gebhardt, Helbig, Karsch, Kluge, Kraft, Krause, Lessmann, Masood, Meister, Metzkes-Ng, Nossula, Pawelke, Pietzsch, Püschel, Reimold, Rehwald, Richter, Schlenvoigt, Schramm, Umlandt, Ziegler, Zeil and Beyreuther4]. As application-readiness is reached for LPA protons, technological developments not only focus on the primary source and according diagnostics but have also diversified to a broad range of dedicated setups for the specific application fields. For radiobiological studies, these developments include dedicated beamlines for protons[
Reference Aymar, Becker, Boogert, Borghesi, Bingham, Brenner, Burrows, Ettlinger, Dascalu, Gibson, Greenshaw, Gruber, Gujral, Hardiman, Hughes, Jones, Kirkby, Kurup, Lagrange, Long, Luk, Matheson, McKenna, McLauchlan, Najmudin, Lau, Parsons, Pasternak, Pozimski, Prise, Puchalska, Ratoff, Schettino, Shields, Smith, Thomason, Towe, Weightman, Whyte and Xiao5–
Reference Bin, Huebl, Mao, Nakamura, Geulig, Chang, Ji, He, Chant, Kober, Gonsalves, Bulanov, Celniker, Schroeder, Geddes, Esarey, Simmons, Schenkel, Blakely, Steinke and Snijders9], dosimetric systems[
Reference Richter, Karsch, Dammene, Kraft, Metzkes, Schramm, Schürer, Sobiella, Weber, Zeil and Pawelke10–
Reference Reimold, Assenbaum, Bernert, Beyreuther, Brack, Karsch, Kraft, Kroll, Nossula, Pawelke, Rehwald, Schlenvoigt, Schramm, Umlandt, Zeil, Ziegler and Metzkes-Ng13] and beam monitoring approaches[
Reference Haffa, Yang, Bin, Lehrack, Brack, Ding, Englbrecht, Gao, Gebhard, Gilljohann, Götzfried, Hartmann, Herr, Hilz, Kraft, Kreuzer, Kroll, Lindner, Metzkes-Ng, Ostermayr, Ridente, Rösch, Schilling, Schlenvoigt, Speicher, Taray, Würl, Zeil, Schramm, Karsch, Parodi, Bolton, Assmann and Schreiber14–
Reference Reimold, Assenbaum, Bernert, Beyreuther, Brack, Karsch, Kraft, Kroll, Loeser, Nossula, Pawelke, Püschel, Schlenvoigt, Schramm, Umlandt, Zeil, Ziegler and Metzkes-Ng17], all contributing to the ability to perform sophisticated experimental studies.
$\sim$
Hz) laser systems, irradiation of mm-scale radiobiological samples is possible. Current radiobiological studies at LPA proton sources hence focus on small animal irradiations in a dose range from approximately 100 mGy to multi-10 Gy[
Reference Kroll, Brack, Bernert, Bock, Bodenstein, Brüchner, Cowan, Gaus, Gebhardt, Helbig, Karsch, Kluge, Kraft, Krause, Lessmann, Masood, Meister, Metzkes-Ng, Nossula, Pawelke, Pietzsch, Püschel, Reimold, Rehwald, Richter, Schlenvoigt, Schramm, Umlandt, Ziegler, Zeil and Beyreuther4]. As application-readiness is reached for LPA protons, technological developments not only focus on the primary source and according diagnostics but have also diversified to a broad range of dedicated setups for the specific application fields. For radiobiological studies, these developments include dedicated beamlines for protons[
Reference Aymar, Becker, Boogert, Borghesi, Bingham, Brenner, Burrows, Ettlinger, Dascalu, Gibson, Greenshaw, Gruber, Gujral, Hardiman, Hughes, Jones, Kirkby, Kurup, Lagrange, Long, Luk, Matheson, McKenna, McLauchlan, Najmudin, Lau, Parsons, Pasternak, Pozimski, Prise, Puchalska, Ratoff, Schettino, Shields, Smith, Thomason, Towe, Weightman, Whyte and Xiao5–
Reference Bin, Huebl, Mao, Nakamura, Geulig, Chang, Ji, He, Chant, Kober, Gonsalves, Bulanov, Celniker, Schroeder, Geddes, Esarey, Simmons, Schenkel, Blakely, Steinke and Snijders9], dosimetric systems[
Reference Richter, Karsch, Dammene, Kraft, Metzkes, Schramm, Schürer, Sobiella, Weber, Zeil and Pawelke10–
Reference Reimold, Assenbaum, Bernert, Beyreuther, Brack, Karsch, Kraft, Kroll, Nossula, Pawelke, Rehwald, Schlenvoigt, Schramm, Umlandt, Zeil, Ziegler and Metzkes-Ng13] and beam monitoring approaches[
Reference Haffa, Yang, Bin, Lehrack, Brack, Ding, Englbrecht, Gao, Gebhard, Gilljohann, Götzfried, Hartmann, Herr, Hilz, Kraft, Kreuzer, Kroll, Lindner, Metzkes-Ng, Ostermayr, Ridente, Rösch, Schilling, Schlenvoigt, Speicher, Taray, Würl, Zeil, Schramm, Karsch, Parodi, Bolton, Assmann and Schreiber14–
Reference Reimold, Assenbaum, Bernert, Beyreuther, Brack, Karsch, Kraft, Kroll, Loeser, Nossula, Pawelke, Püschel, Schlenvoigt, Schramm, Umlandt, Zeil, Ziegler and Metzkes-Ng17], all contributing to the ability to perform sophisticated experimental studies.
Radiobiological studies and other experiments relying on the generation of application-specific volumetric dose distributions (e.g., material analysis[ Reference Barberio, Veltri, Scisciò and Antici18]) from single LPA proton bunches call for a reliable method to measure said volumetric dose distributions. For analysis purposes, a volumetric dose distribution is generally divided into lateral components and a depth dose profile, the latter being determined by the spectral components contained in the proton bunch depositing its energy in the sample. In contrast to spectrally stable proton sources such as (radiotherapy) cyclotrons, the inherent bunch-to-bunch fluctuations of the spectral intensity present at LPA proton sources require characterization with single-bunch resolution. The available methods include stacks of radiochromic films (RCFs)[ Reference Bolton, Borghesi, Brenner, Carroll, De Martinis, Fiorini, Flacco, Floquet, Fuchs, Gallegos, Giove, Green, Green, Jones, Kirby, McKenna, Neely, Nuesslin, Prasad, Reinhardt, Roth, Schramm, Scott, Ter-Avetisyan, Tolley, Turchetti and Wilkens19], ultrasound-based methods[ Reference Haffa, Yang, Bin, Lehrack, Brack, Ding, Englbrecht, Gao, Gebhard, Gilljohann, Götzfried, Hartmann, Herr, Hilz, Kraft, Kreuzer, Kroll, Lindner, Metzkes-Ng, Ostermayr, Ridente, Rösch, Schilling, Schlenvoigt, Speicher, Taray, Würl, Zeil, Schramm, Karsch, Parodi, Bolton, Assmann and Schreiber14, Reference Gerlach, Pinto, Kurichiyanil, Grau, Hérault, Hillbrand, Poulsen, Safai, Schippers, Schwarz, Søndergaard, Tommasino, Verroi, Vidal, Yohannes, Schreiber and Parodi15] or the prediction of the depth dose distributions based on a spectral time-of-flight (ToF) measurement[ Reference Reimold, Assenbaum, Bernert, Beyreuther, Brack, Karsch, Kraft, Kroll, Loeser, Nossula, Pawelke, Püschel, Schlenvoigt, Schramm, Umlandt, Zeil, Ziegler and Metzkes-Ng17]. With currently achievable mm-scale spatial dose distributions, sub-mm spatial resolution with a sensitivity of approximately 100 mGy is required, ideally with the capability for approximately Hz repetition rate operation. Plastic scintillators, widely applied for LPA proton detection[ Reference Green, Borghesi, Brenner, Carroll, Dover, Foster, Gallegos, Green, Kirby, Kirkby, McKenna, Merchant, Najmudin, Palmer, Parker, Prasad, Quinn, Rajeev, Read, Romagnani, Schreiber, Streeter, Tresca, Wahlström, Zepf and Neely20– Reference Mariscal, Djordjevíc, Grace, Hollinger, Ma, Scott, Song, Simpson, Rocca and Wang28], make an ideal candidate for a detector with these properties. They offer an instantaneous light output on the ns-timescale after dose deposition, have a density close to water and can flexibly be applied in shapes adapted to the specific detector setup. Due to their transparency and hence high transmission for their own emitted spectrum, optical scintillators are optimal for tomography methods applied to spatially resolve volumetric distributions.
In this publication, we present the compact and robust miniSCIDOM, a scintillator-based tomograph for the reconstruction of dose distributions generated by single LPA proton bunches. The detector principle is based on emission tomography from a hexagonally shaped scintillator, as prototyped by Kroll et al. [
Reference Kroll, Pawelke and Karsch29] for quality assurance at medical proton accelerators. Adaption of the approach to LPA requirements allows for the miniaturization to a reconstruction volume of approximately 1 cm
![]() ${}^3$
so that a single camera coupled with a bi-telecentric objective can image all four parallel 2D projections needed for reconstruction. The setup was characterized at a proton therapy cyclotron and an LPA proton source, yielding a spatial resolution better than 500
${}^3$
so that a single camera coupled with a bi-telecentric objective can image all four parallel 2D projections needed for reconstruction. The setup was characterized at a proton therapy cyclotron and an LPA proton source, yielding a spatial resolution better than 500
![]() $\unicode{x3bc}$
m and a lower detection limit of 100 mGy. Furthermore, the study focused on characterizing the ionization quenching typical for plastic scintillators, an effect that results in a reduction of light output as the proton’s ionization density along its track increases towards the stopping point. We find that the ultra-high dose rate achieved at LPA proton sources changes the ionization quenching behaviour compared to lower dose rate irradiations at the proton therapy cyclotron.
$\unicode{x3bc}$
m and a lower detection limit of 100 mGy. Furthermore, the study focused on characterizing the ionization quenching typical for plastic scintillators, an effect that results in a reduction of light output as the proton’s ionization density along its track increases towards the stopping point. We find that the ultra-high dose rate achieved at LPA proton sources changes the ionization quenching behaviour compared to lower dose rate irradiations at the proton therapy cyclotron.
2. Detector design and data processing
2.1. Detector setup
The miniSCIDOM detector (Figure 1) consists of a signal emitting and a signal detecting component and has a footprint of 70 mm diameter and a height of 370 mm. The signal emitting component comprises a plastic scintillator (EJ-200, Eljen Technologies[
30]) in the shape of a regular hexagonal prism with 10 mm hexagon side length and a thickness of 11 mm. When ionizing radiation impinges on the scintillator, it emits (luminescent) light (
![]() $\sim$
2 ns decay time) in the visible range centred around 425 nm. The light emitted from the scintillator travels to the detecting component either directly (scintillator top) or via three square ultraviolet (UV)-enhanced aluminium mirrors (Thorlabs PFSQ05-03-F01 & PFSQ10-03-F01) for two side projections (mirror 1/3 in Figure 1) and the beam axis projection (mirror 2 in Figure 1). The side and beam axis mirrors are tilted by 30° and 45°, respectively. The exposed scintillator surfaces are polished to couple the light out efficiently.
$\sim$
2 ns decay time) in the visible range centred around 425 nm. The light emitted from the scintillator travels to the detecting component either directly (scintillator top) or via three square ultraviolet (UV)-enhanced aluminium mirrors (Thorlabs PFSQ05-03-F01 & PFSQ10-03-F01) for two side projections (mirror 1/3 in Figure 1) and the beam axis projection (mirror 2 in Figure 1). The side and beam axis mirrors are tilted by 30° and 45°, respectively. The exposed scintillator surfaces are polished to couple the light out efficiently.

Figure 1 The miniSCIDOM detector consists of a plastic scintillator shaped like a regular hexagonal prism. It is imaged via three mirrors, a bi-telecentric objective and a CCD camera.
The core detecting component is a bi-telecentric objective (TC13056, Opto Engineering), which only accepts rays parallel to its main optical axis and hence images 2D parallel projections of the scintillation light. A charge-coupled device (CCD) camera coupled directly to the objective records a single image containing all four projections. The objective is designed for a fixed object distance of 157.8 mm and features a fixed magnification of 0.084 so that the camera pixel size (approximately 5
![]() $\unicode{x3bc}$
m
$\unicode{x3bc}$
m
![]() $\times$
5
$\times$
5
![]() $\unicode{x3bc}$
m) defines the achievable spatial resolution to 60
$\unicode{x3bc}$
m) defines the achievable spatial resolution to 60
![]() $\unicode{x3bc}$
m for the 2D projections. By using optical filters between the scintillator and the objective, the emitted scintillation light can either be spectrally filtered or attenuated to match the camera’s sensitivity and dynamic range. This allows for detector operation over the full range of deposited doses relevant for, for example, radiobiological studies.
$\unicode{x3bc}$
m for the 2D projections. By using optical filters between the scintillator and the objective, the emitted scintillation light can either be spectrally filtered or attenuated to match the camera’s sensitivity and dynamic range. This allows for detector operation over the full range of deposited doses relevant for, for example, radiobiological studies.
2.2. Signal reconstruction
The scintillator and imaging geometry defines three projection angles around the beam axis (0°, 120°, 240°) and a fourth projection along the beam axis. Figure 2(a) shows these four projections recorded in a single camera image. The coloured boxes mark the regions of interest (ROIs) for each projection that contribute to the reconstruction of the volumetric light distribution and define the reconstruction volume. The reconstruction algorithm performs best in the region where all projections overlap (Figures 2(b) and 2(c)), which results in a usable detector aperture of 10 mm diameter. The scintillator length of 11 mm is equivalent to the range of protons with a kinetic energy of 35 MeV.

Figure 2 Signal reconstruction. (a) False-colour raw data CCD camera image and selection of the different regions of interest (ROIs) for the four projections. The signal outside the ROI for the 0° projection corresponds to the signal imaged through the scintillator hexagon faces adjacent to the scintillator surface analysed for a specific projection. (b) Beam axis view of the scintillator with the lateral projection regions marked. The region where the lateral projections overlap (red hexagonal marking) is the lateral reconstruction area. (c) Volumetric representation of the reconstruction volume.
An iterative algorithm based on maximum-likelihood expectation maximization (MLEM) has been implemented in Python 3 to reconstruct the volumetric light distribution from the imaged projections. The iterative algorithm corrects a predicted volumetric light distribution by comparing the respective predicted projections with the measured projections and by subsequently applying a correction matrix to the predicted light distribution. To estimate the uncertainty for the reconstructed volumetric light distribution, the ratio of predicted and measured projections is used, averaged over all four projections (Figure 2(a)).
The reconstruction itself is preceded by several image preprocessing steps. Firstly, the ROIs (as shown in Figure 2(a)) are selected from the raw images by setting the ROI coordinates manually to correct for displacements or tilts introduced by the detector setup. The projection images are then filtered for noise reduction caused by salt-and-pepper noise (hot pixels) using a median filter (
![]() $2\times 2\ {\mathrm{pixel}}^2$
kernel, with signal threshold). Moreover, the projections imaged via mirrors are corrected for the mirror reflectivity to ensure the same signal level as the directly imaged 0° projection. Further image manipulations, such as translations, rotations, and image scaling, are introduced to compensate for small camera misalignments that cannot be eliminated completely due to the limited possibility for mechanical adjustment within the miniSCIDOM setup. These alignments are performed once after detector setup at an experimental site.
$2\times 2\ {\mathrm{pixel}}^2$
kernel, with signal threshold). Moreover, the projections imaged via mirrors are corrected for the mirror reflectivity to ensure the same signal level as the directly imaged 0° projection. Further image manipulations, such as translations, rotations, and image scaling, are introduced to compensate for small camera misalignments that cannot be eliminated completely due to the limited possibility for mechanical adjustment within the miniSCIDOM setup. These alignments are performed once after detector setup at an experimental site.
2.3. Correcting for ionization quenching
The light distribution emitted by a plastic scintillator upon irradiation with an energetic proton bunch is not linearly proportional to the absorbed dose. This results from an effect termed ‘ionization quenching’, which describes the scintillator’s light output dependency on ionization density along the proton track. As the ionization density increases towards a proton’s stopping point, the contribution of non-radiative de-excitation of the scintillator increases, leading to a decrease of light output[ Reference Birks31]. Ionization quenching can be quantified by a first-order model by Birks:
 $$\begin{align}\mathrm{d}L/\mathrm{d}x=\frac{S\cdot \left(\frac{\mathrm{d}E}{\mathrm{d}x}\right)}{1+ kB\cdot \left(\frac{\mathrm{d}E}{\mathrm{d}x}\right)},\end{align}$$
$$\begin{align}\mathrm{d}L/\mathrm{d}x=\frac{S\cdot \left(\frac{\mathrm{d}E}{\mathrm{d}x}\right)}{1+ kB\cdot \left(\frac{\mathrm{d}E}{\mathrm{d}x}\right)},\end{align}$$
where the light output per unit path length is
![]() $\mathrm{d}L/\mathrm{d}x$
, the unquenched scintillator light output is
$\mathrm{d}L/\mathrm{d}x$
, the unquenched scintillator light output is
![]() $S$
, the linear energy transfer (LET)
$S$
, the linear energy transfer (LET)
![]() $\mathrm{d}E/\mathrm{d}x$
is proportional to the ionization density and the material-dependent Birks constant is
$\mathrm{d}E/\mathrm{d}x$
is proportional to the ionization density and the material-dependent Birks constant is
![]() $kB$
. For the polyvinyltoluene-based plastic scintillator used in the miniSCIDOM,
$kB$
. For the polyvinyltoluene-based plastic scintillator used in the miniSCIDOM,
![]() $kB$
was determined to
$kB$
was determined to
![]() $kB=0.207\;\mathrm{mm}\;{\mathrm{MeV}}^{-1}$
[
Reference Torrisi32].
$kB=0.207\;\mathrm{mm}\;{\mathrm{MeV}}^{-1}$
[
Reference Torrisi32].
When employing plastic scintillators to measure and reconstruct spatial dose distributions generated by protons, ionization quenching needs to be taken into account. Correction for the effect as described by Equation (1) requires prior knowledge of the local LET distribution within the scintillator volume and hence of the proton spectrum generating the respective dose distribution. In general, Monte Carlo (MC) simulations of the incoming proton bunch and the full beam transport at the accelerator setup are required to derive LET values for light output corrections.

Figure 3 miniSCIDOM depth dose measurements at a proton therapy cyclotron. The data show the miniSCIDOM reconstruction (marked as MS in the legend, light blue), the simulated depth dose curve (red), the radiochromic film (RCF) measurement (green), the simulated fluence-weighted linear energy transfer (LET, pink) and the LET-corrected miniSCIDOM measurement (orange). The depth dose profiles for the miniSCIDOM and RCF are averaged over a circular ROI with 5 mm diameter. All depth dose curves are individually normalized. (a) Pristine Bragg peak (PBP) irradiation of the miniSCIDOM. (b) Spread-out Bragg peak (SOBP) irradiation of the miniSCIDOM.
3. miniSCIDOM characterization at a proton therapy cyclotron
3.1. Experiment
Characterization measurements with the miniSCIDOM were performed at the University Proton Therapy Dresden (UPTD, Dresden, Germany). Here, an experimental hall equipped with a horizontal fixed-beam proton beamline for the isochronous cyclotron Cyclone 230 (Proteus Plus clinical facility, IBA) is available for multidisciplinary research[ Reference Helmbrecht, Baumann, Enghardt, Fiedler, Krause and Lühr33]. Besides determining the spatial resolution properties of the detector, a key task of the experiment was to precisely measure the ionization quenching as it affects the reconstruction of volumetric dose distributions. To consider both the case of a locally almost uniform and a locally mixed LET, the miniSCIDOM was exposed to monoenergetic protons generating a pristine Bragg peak (PBP) in the scintillator volume as well as polyenergetic protons forming a so-called spread-out Bragg peak (SOBP). The latter case corresponds to the realistic scenario in which the miniSCIDOM is implemented at the LPA proton beamline[ Reference Kroll, Brack, Bernert, Bock, Bodenstein, Brüchner, Cowan, Gaus, Gebhardt, Helbig, Karsch, Kluge, Kraft, Krause, Lessmann, Masood, Meister, Metzkes-Ng, Nossula, Pawelke, Pietzsch, Püschel, Reimold, Rehwald, Richter, Schlenvoigt, Schramm, Umlandt, Ziegler, Zeil and Beyreuther4].
To measure a PBP, protons with a kinetic energy of 90 MeV irradiated the miniSCIDOM after traversing a set of range absorbers (45 mm of polycarbonate (PC) and 5.2 mm of acrylic glass) applied to place the PBP inside the miniSCIDOM reconstruction volume. SOBP measurements used the double-scattering setup described in Ref. [Reference Helmbrecht, Baumann, Enghardt, Fiedler, Krause and Lühr33] to generate a 20 mm wide SOBP from monoenergetic 150 MeV protons, shifted into the miniSCIDOM reconstruction volume by a 90 mm thick PC range absorber. For both setups, a final aperture with 7 mm diameter was placed in front of the miniSCIDOM to restrict the lateral beam profile to the reconstruction volume.
To derive the dose deposition inside the scintillator and the according LET distribution, both irradiation scenarios (comprising the proton bunch parameters and the beamline setup) were modelled using the MC simulation toolkit TOPAS[
34]. The simulations were benchmarked against measurements of the final volumetric dose distributions at the miniSCIDOM position using stacks of RCF (type EBT3, GafChromic[
35]). For both cases, the fluence-weighted
![]() ${\mathrm{LET}}_{\mathrm{t}}$
(also referred to as track-weighted[
Reference Smith, Winterhalter, Underwood, Aitkenhead, Richardson, Merchant, Kirkby, Kirby and Mackay36]) is applied as a measure for the average local LET. The
${\mathrm{LET}}_{\mathrm{t}}$
(also referred to as track-weighted[
Reference Smith, Winterhalter, Underwood, Aitkenhead, Richardson, Merchant, Kirkby, Kirby and Mackay36]) is applied as a measure for the average local LET. The
![]() ${\mathrm{LET}}_{\mathrm{t}}$
uses the local fluence of every proton energy bin as the weighting factor for the average LET at a certain position.
${\mathrm{LET}}_{\mathrm{t}}$
uses the local fluence of every proton energy bin as the weighting factor for the average LET at a certain position.
3.2. Results: ionization quenching
Figure 3 summarizes simulation and experimental results showing the depth dose distributions of the PBP and SOBP and the
![]() ${\mathrm{LET}}_{\mathrm{t}}$
. The volumetric light distribution measured by the miniSCIDOM was reconstructed and averaged within a 5 mm diameter lateral ROI to obtain a depth profile. The signal standard deviation within the lateral ROI was evaluated for each depth layer and amounts to less than 3% for the PBP and less than 5% for the SOBP case (averaged over all depth layers). In addition, the reconstruction algorithm yields an uncertainty of less than 3%. Both uncertainties are combined in the error bars shown with the miniSCIDOM data. Note that all data are normalized to their respective peak. The MC simulation (red) and RCF measurement result (green) show excellent agreement, validating the use of the simulated LET distributions to correct for ionization quenching in the miniSCIDOM detector. The error bars for the RCF measurement represent the uncertainty of the dose to water calibration of the films of 6%. Before applying the quenching correction, the miniSCIDOM depth distribution deviates significantly from the simulated and RCF distributions in both the PBP and SOBP cases in the entrance region and towards the distal edge. Once corrected for ionization quenching according to Equation (1), the miniSCIDOM reconstruction (orange) fits the simulated curve and lies almost completely inside the error bars of the RCF measurement for both cases.
${\mathrm{LET}}_{\mathrm{t}}$
. The volumetric light distribution measured by the miniSCIDOM was reconstructed and averaged within a 5 mm diameter lateral ROI to obtain a depth profile. The signal standard deviation within the lateral ROI was evaluated for each depth layer and amounts to less than 3% for the PBP and less than 5% for the SOBP case (averaged over all depth layers). In addition, the reconstruction algorithm yields an uncertainty of less than 3%. Both uncertainties are combined in the error bars shown with the miniSCIDOM data. Note that all data are normalized to their respective peak. The MC simulation (red) and RCF measurement result (green) show excellent agreement, validating the use of the simulated LET distributions to correct for ionization quenching in the miniSCIDOM detector. The error bars for the RCF measurement represent the uncertainty of the dose to water calibration of the films of 6%. Before applying the quenching correction, the miniSCIDOM depth distribution deviates significantly from the simulated and RCF distributions in both the PBP and SOBP cases in the entrance region and towards the distal edge. Once corrected for ionization quenching according to Equation (1), the miniSCIDOM reconstruction (orange) fits the simulated curve and lies almost completely inside the error bars of the RCF measurement for both cases.
Differences between the miniSCIDOM and simulated distribution remain in the entrance region and behind the PBP’s distal edge (depth
![]() $>$
6 mm in Figure 3(a)). In the entrance region, very close to the front scintillator surface, the primary scintillation signal is distorted by back-reflections from the scintillator surface as well as by slight misalignments of the scintillator edge with respect to the imaging objective. Behind the PBP’s distal edge, the discrepancy results from the background signal in the miniSCIDOM detector that is generated from scintillation light scattered from the scintillator’s rear surface. If the actual scintillation signal reaches close to the rear surface, a signal distortion can be observed. In summary, the experimental results obtained at the cyclotron proton source validate the application of the Birks model to correct for ionization quenching in PBP and SOBP LET distributions.
$>$
6 mm in Figure 3(a)). In the entrance region, very close to the front scintillator surface, the primary scintillation signal is distorted by back-reflections from the scintillator surface as well as by slight misalignments of the scintillator edge with respect to the imaging objective. Behind the PBP’s distal edge, the discrepancy results from the background signal in the miniSCIDOM detector that is generated from scintillation light scattered from the scintillator’s rear surface. If the actual scintillation signal reaches close to the rear surface, a signal distortion can be observed. In summary, the experimental results obtained at the cyclotron proton source validate the application of the Birks model to correct for ionization quenching in PBP and SOBP LET distributions.
3.3. Results: spatial resolution
The spatial resolution of the miniSCIDOM was tested with a perforated aluminium collimator inserted into the proton beam path in front of the detector, generating proton minibeams with 600
![]() $\unicode{x3bc}$
m diameter and 1 mm centre-to-centre distance. The measurements with the collimator were performed in the PBP setting as described above. RCF stacks irradiated at the same position as the miniSCIDOM detector served as reference. Figure 4 compares the results for an RCF stack (Figure 4(a)) re-binned to fit the miniSCIDOM resolution with reconstructed miniSCIDOM data (Figure 4(b)). The miniSCIDOM can clearly resolve all beams within its reconstruction volume. A Gaussian fit function is used to estimate the full width at half maximum (FWHM) of the individual minibeams reconstructed by the miniSCIDOM, yielding a mean value of 460
$\unicode{x3bc}$
m diameter and 1 mm centre-to-centre distance. The measurements with the collimator were performed in the PBP setting as described above. RCF stacks irradiated at the same position as the miniSCIDOM detector served as reference. Figure 4 compares the results for an RCF stack (Figure 4(a)) re-binned to fit the miniSCIDOM resolution with reconstructed miniSCIDOM data (Figure 4(b)). The miniSCIDOM can clearly resolve all beams within its reconstruction volume. A Gaussian fit function is used to estimate the full width at half maximum (FWHM) of the individual minibeams reconstructed by the miniSCIDOM, yielding a mean value of 460
![]() $\unicode{x3bc}$
m. The minibeam diameter is hence broadened by 15%, a value that is in agreement with the targeted spatial resolution in the 500
$\unicode{x3bc}$
m. The minibeam diameter is hence broadened by 15%, a value that is in agreement with the targeted spatial resolution in the 500
![]() $\unicode{x3bc}$
m range.
$\unicode{x3bc}$
m range.

Figure 4 Characterization of the spatial resolution with a perforated aluminium collimator, generating proton minibeams with 600
![]() $\unicode{x3bc}$
m diameter and 1 mm centre-to-centre spacing. (a) Measurement with a stack of radiochromic films (RCFs), where representative slices for the top, side and beam axis views are shown. (b) Measurement with the miniSCIDOM detector, where representative slices for the top, side and beam axis views derived from the reconstruction are shown. (c) Comparison between lateral profiles through the top views for the RCF and miniSCIDOM. The profiles are obtained at a fixed depth position (z = 3 mm) and integrated over 3 pixels in the x direction. Note that due to its limited reconstruction volume, the miniSCIDOM only resolves eight minibeams, whereas the RCF stack resolves 10. The minibeams at positions y = 11 mm and y = 12 mm are artefact minibeams imaged from a hexagon face adjacent to the scintillator surface analysed for the projection under consideration.
$\unicode{x3bc}$
m diameter and 1 mm centre-to-centre spacing. (a) Measurement with a stack of radiochromic films (RCFs), where representative slices for the top, side and beam axis views are shown. (b) Measurement with the miniSCIDOM detector, where representative slices for the top, side and beam axis views derived from the reconstruction are shown. (c) Comparison between lateral profiles through the top views for the RCF and miniSCIDOM. The profiles are obtained at a fixed depth position (z = 3 mm) and integrated over 3 pixels in the x direction. Note that due to its limited reconstruction volume, the miniSCIDOM only resolves eight minibeams, whereas the RCF stack resolves 10. The minibeams at positions y = 11 mm and y = 12 mm are artefact minibeams imaged from a hexagon face adjacent to the scintillator surface analysed for the projection under consideration.
Besides the minibeam broadening, comparison of the top and beam axis views clearly shows a stronger merging of the individual proton minibeams in the case of the miniSCIDOM. Whereas the signal recorded with the RCF shows a peak-to-valley ratio of 5, it is reduced to 1.6 for the miniSCIDOM (Figure 4(c)). The effect is dominated by scattering of the scintillation light inside the scintillator volume, but a contribution from the limited number of projections available for signal reconstruction cannot be excluded. The lateral spatial resolution of the miniSCIDOM detector does not depend on the spectral distribution of the proton bunches applied and is hence the same for LPA protons.
4. miniSCIDOM operation at a laser plasma accelerator proton source
4.1. Experiment
The miniSCIDOM detector was integrated into the ALBUS-2S beamline[
Reference Brack, Kroll, Gaus, Bernert, Beyreuther, Cowan, Karsch, Kraft, Kunz-Schughart, Lessmann, Metzkes-Ng, Obst-Huebl, Pawelke, Rehwald, Schlenvoigt, Schramm, Sobiella, Szabó, Ziegler and Zeil6] operated at the Draco PW high-power laser system at Helmholtz-Zentrum Dresden–Rossendorf[
Reference Schramm, Bussmann, Irman, Siebold, Zeil, Albach, Bernert, Bock, Brack, Branco, Couperus, Cowan, Debus, Eisenmann, Garten, Gebhardt, Grams, Helbig, Huebl, Kluge, Köhler, Krämer, Kraft, Kroll, Kuntzsch, Lehnert, Loeser, Metzkes, Michel, Obst, Pausch, Rehwald, Sauerbrey, Schlenvoigt, Steiniger and Zarini37,
Reference Ziegler, Albach, Bernert, Bock, Brack, Cowan, Dover, Garten, Gaus, Gebhardt, Goethel, Helbig, Irman, Kiriyama, Kluge, Kon, Kraft, Kroll, Loeser, Metzkes-Ng, Nishiuchi, Obst-Huebl, Püschel, Rehwald, Schlenvoigt, Schramm and Zeil38]. Based on the chromatic focusing properties of two pulsed solenoids, ALBUS-2S produces homogeneous mm-scale volumetric dose distributions at an in-air irradiation site from the angular and spectral broadband LPA proton bunch (Figure 5(a)). Spectral filtering apertures and scattering foils finetune the transported proton spectrum to form an application-adapted dose distribution[
Reference Kroll, Brack, Bernert, Bock, Bodenstein, Brüchner, Cowan, Gaus, Gebhardt, Helbig, Karsch, Kluge, Kraft, Krause, Lessmann, Masood, Meister, Metzkes-Ng, Nossula, Pawelke, Pietzsch, Püschel, Reimold, Rehwald, Richter, Schlenvoigt, Schramm, Umlandt, Ziegler, Zeil and Beyreuther4]. For the miniSCIDOM tests, single-peak proton bunches centred around 22 MeV with a bandwidth (FWHM) of approximately 10 MeV and a dose of approximately 1 Gy are applied. The bunch duration at the irradiation site is 20 ns, yielding a bunch dose rate of
![]() ${10}^8\ \mathrm{Gy}\;{\mathrm{s}}^{-1}$
.
${10}^8\ \mathrm{Gy}\;{\mathrm{s}}^{-1}$
.

Figure 5 miniSCIDOM measurements at an LPA proton source. (a) Experimental setup including the LPA proton source driven by the Draco PW laser system and the ALBUS-2S beamline. A time-of-flight (ToF) spectrometer serves as a spectrally resolving beam monitoring system. (b) Comparison of an RCF stack irradiation with seven proton bunches and the according depth dose simulated based on the seven proton bunch spectra measured by the ToF spectrometer. The error bar associated with the simulated dose represents the sum of the energy uncertainty and proton number calibration uncertainty. The error bar associated with the measured dose represents the calibration uncertainty of 6%. (c) Absolutely calibrated ToF proton energy spectra (
![]() $\mathrm{d}{N}_{\mathrm{p}}/\mathrm{d}{E}_{\mathrm{p}}$
) for three single proton bunches as prepared by the ALBUS-2S beamline. The error bars take into account the spectral resolution of the ToF spectrometer and the uncertainty of the absolute calibration of the spectra. (d) Comparison of the depth dose distribution inside the miniSCIDOM as predicted based on the measured ToF proton spectra and the measurement with the miniSCIDOM. The error bars for the ToF measurement represent the propagation of the uncertainties in the spectral measurement. (e) For proton bunch 3, the depth dose curves from the miniSCIDOM measurement (MS, light blue) and the ToF-based prediction (blue) are shown. Moreover, the depth dose distribution is simulated including ionization quenching (red), and a correction for ionization quenching (orange) based on the fluence-weighted linear energy transfer (LET, pink) is applied to the miniSCIDOM data.
$\mathrm{d}{N}_{\mathrm{p}}/\mathrm{d}{E}_{\mathrm{p}}$
) for three single proton bunches as prepared by the ALBUS-2S beamline. The error bars take into account the spectral resolution of the ToF spectrometer and the uncertainty of the absolute calibration of the spectra. (d) Comparison of the depth dose distribution inside the miniSCIDOM as predicted based on the measured ToF proton spectra and the measurement with the miniSCIDOM. The error bars for the ToF measurement represent the propagation of the uncertainties in the spectral measurement. (e) For proton bunch 3, the depth dose curves from the miniSCIDOM measurement (MS, light blue) and the ToF-based prediction (blue) are shown. Moreover, the depth dose distribution is simulated including ionization quenching (red), and a correction for ionization quenching (orange) based on the fluence-weighted linear energy transfer (LET, pink) is applied to the miniSCIDOM data.
A scintillator-based ToF spectrometer, installed downstream from all beam shaping elements, is the established spectral beam monitoring device at ALBUS-2S. It provides online transmission measurements of each single proton bunch sent to the irradiation site[ Reference Reimold, Assenbaum, Bernert, Beyreuther, Brack, Karsch, Kraft, Kroll, Loeser, Nossula, Pawelke, Püschel, Schlenvoigt, Schramm, Umlandt, Zeil, Ziegler and Metzkes-Ng17]. A benchmarked workflow for post-processing of the ToF spectra enables the MC simulation-based (FLUKA version 4-0.0[ Reference Battistoni, Bauer, Boehlen, Cerutti, Chin, Augusto, Ferrari, Ortega, Kozlowska, Magro, Mairani, Parodi, Sala, Schoofs, Tessonnier and Vlachoudis39]) forward-calculation of the depth dose distribution at the irradiation site as resulting from a specific spectral proton bunch distribution[ Reference Reimold, Assenbaum, Bernert, Beyreuther, Brack, Karsch, Kraft, Kroll, Loeser, Nossula, Pawelke, Püschel, Schlenvoigt, Schramm, Umlandt, Zeil, Ziegler and Metzkes-Ng17]. The forward-calculations are benchmarked against measurements of the depth dose distribution with stacks of RCFs, as illustrated in Figure 5(b). Note that the RCF stack was irradiated with seven consecutive proton bunches from the ALBUS-2S beamline to reach a dose level at which the dose uncertainty of the calibrated RCF stacks is reduced to the level of 6%. The forward-calculation based on the individually measured ToF spectra considers each of the proton bunches applied to the RCF stack. The forward-calculation reproduces the measured depth dose distribution well within the dose uncertainty range of the RCF stack measurement, confirming the depth dose prediction capabilities of the ToF spectrometer. It is hence the ideal reference device for miniSCIDOM measurements testing the reconstruction capabilities of depth dose distributions from ultra-high dose LPA proton bunches and ionization quenching in a mixed-LET irradiation field.
4.2. Results: ionization quenching
The miniSCIDOM was placed at the irradiation site behind a stainless steel aperture (8 mm thickness) with 7 mm diameter, matching the irradiated detector volume with its reconstruction volume. Three individual proton bunches differing in spectral shape were consecutively applied to the miniSCIDOM, the according spectra measured with the ToF spectrometer being shown in Figure 5(c). To generate depth dose distributions from the miniSCIDOM measurements, the volumetric scintillation light distributions were reconstructed. The uncertainty of the reconstructed volumetric light distribution amounts to less than 4%. Subsequently, the signal was evaluated along the beam axis (depth direction) and averaged over a lateral circular ROI with 5 mm diameter centred on the beam axis. Figure 5(d) compares the depth dose distributions for the three proton bunches measured with the miniSCIDOM detector with the forward-calculated depth dose distributions based on the spectra in Figure 5(c). For representation, the miniSCIDOM depth dose curves are normalized to the according ToF-measured data. Both curves show a perfect shape agreement within the error bars of the forward-calculation. This result emphasizes the applicability of the miniSCIDOM detector in measuring depth dose distributions at LPA proton sources, down to dose levels of 100 mGy as present in the distal edge region of the dose distributions measured. The lower detection threshold of the detector results from the scintillator’s conversion efficiency to optical emission from deposited energy, the efficiency of the imaging system and the CCD camera’s sensitivity. It is in agreement with the detector’s intended application for radiobiological studies with LPA protons.
It needs to be highlighted that the agreement of the results from miniSCIDOM-measured and forward-calculated depth dose distributions is unexpected according to the findings from the cyclotron measurements, which clearly show the requirement for an ionization quenching correction for the miniSCIDOM measurements. A representative proton bunch is analysed in more detail in Figure 5(e), where the light and dark blue lines reproduce the data for bunch 3 from Figure 5(d). The fluence-weighted
![]() ${\mathrm{LET}}_{\mathrm{t}}$
is derived from the ToF spectral data and features a clear increase towards the distal edge of the dose distribution (pink line). Applying the
${\mathrm{LET}}_{\mathrm{t}}$
is derived from the ToF spectral data and features a clear increase towards the distal edge of the dose distribution (pink line). Applying the
![]() ${\mathrm{LET}}_{\mathrm{t}}$
-based ionization quenching correction to the measured depth distribution (light blue) following Equation (1) yields a clear overestimation of the local depth dose (orange). On the other hand, MC simulations of the scintillator response including ionization quenching are performed based on the ToF-provided proton bunch spectrum (Figure 5(c), bunch 3). The resulting curve (red) yields a clear underestimation of the dose compared to the measurement. In summary, the miniSCIDOM measurements at the LPA proton source indicate that ionization quenching as described by a first-order Birks model (Equation (1)) is not present.
${\mathrm{LET}}_{\mathrm{t}}$
-based ionization quenching correction to the measured depth distribution (light blue) following Equation (1) yields a clear overestimation of the local depth dose (orange). On the other hand, MC simulations of the scintillator response including ionization quenching are performed based on the ToF-provided proton bunch spectrum (Figure 5(c), bunch 3). The resulting curve (red) yields a clear underestimation of the dose compared to the measurement. In summary, the miniSCIDOM measurements at the LPA proton source indicate that ionization quenching as described by a first-order Birks model (Equation (1)) is not present.
5. Discussion of dose rate effects
Besides presenting the dose reconstruction capabilities of the miniSCIDOM detector, the main result of this study concerns the unexpected ionization quenching behaviour observed at the LPA proton source. In contrast, for the proton therapy cyclotron data, ionization quenching is perfectly described by Birks’ model. Applying similar final energy spectra at both proton sources (i.e., similar proton range in the scintillator) leaves the time dependence of dose deposition inside the scintillator as the main difference between both irradiation setups. At the proton therapy cyclotron, 2 ns long bunches at 106 MHz repetition rate are generated. Here the dose rate range of
![]() $0.06$
–
$0.06$
–
![]() $1.86\;\mathrm{Gy}\;{\mathrm{s}}^{-1}$
was explicitly tested and did not show an influence on ionization quenching.
$1.86\;\mathrm{Gy}\;{\mathrm{s}}^{-1}$
was explicitly tested and did not show an influence on ionization quenching.
The dose deposition dynamics for LPA protons is derived from the ToF measurements and according MC simulations. Figure 6(a) shows the depth-resolved dose application on the ns-timescale for an LPA proton bunch. For the analysis, the scintillator depth is divided into 28 virtual layers and the temporal dose deposition for each layer is evaluated. As expected, lower-energy protons arrive last and deposit the majority of dose in the miniSCIDOM’s entrance region, which hence accumulates the dose over the longest time. From the information encoded in Figure 6(a), the depth-resolved dose rate is calculated as the ratio between 80% of the total absorbed dose per layer and the time it takes for the absorbed dose to rise from 10% to 90% (Figure 6(b)). The peak dose rate achieved inside the scintillator volume is approximately
![]() $2.5\times {10}^8\ \mathrm{Gy}\;{\mathrm{s}}^{-1}$
, hence up to a factor
$2.5\times {10}^8\ \mathrm{Gy}\;{\mathrm{s}}^{-1}$
, hence up to a factor
![]() ${10}^8$
higher than what the proton therapy cyclotron provided for the presented experiments.
${10}^8$
higher than what the proton therapy cyclotron provided for the presented experiments.

Figure 6 Analysis of the dose deposition dynamics at the LPA proton source based on Monte Carlo (MC) simulations for bunch 3 from Figure 5. (a) Depth- and time-resolved dose deposition inside the miniSCIDOM for virtual depth layers. (b) The depth-resolved dose rate is calculated as the ratio of 80% of the total absorbed dose per layer and the time it takes for the absorbed dose to rise from 10% to 90%. (c) The depth-resolved proton flux is calculated by taking 80% of the total particle fluence at the corresponding depth and dividing it by the time interval in between which 10% and 90% of the dose are deposited.
The current state of research for ultra-high dose rate irradiation of scintillators is sparse and the topic is to our knowledge mainly discussed in the context of dosimetry and beam monitoring for ultra-high dose rate radiation triggering of the radiobiological FLASH effect[
Reference Esplen, Mendonca and Bazalova-Carter3]. Ref. [Reference Hamel40] suggests that a saturation of the scintillator light output at ultra-high dose rate irradiation similar to ionization quenching might happen. According data only exist for electron irradiations and Di Martino et al. [
Reference Di Martino, Barca, Barone, Bortoli, Borgheresi, De Stefano, Di Francesco, Faillace, Giuliano, Grasso, Linsalata, Marfisi, Migliorati, Pacitti, Palumbo and Felici41] have shown for an organic scintillator-based device that saturation sets in above a dose rate of
![]() ${10}^4\;\mathrm{Gy}\;{\mathrm{s}}^{-1}$
. The effect is attributed to the temporary dead time of the scintillator due to the material’s response time. Favaudon et al. [
Reference Favaudon, Lentz, Heinrich, Patriarca, de Marzi, Fouillade and Dutreix42], on the other hand, have shown linearity for ultra-high dose rate electron irradiation of a gadolinium-based scintillator for dose rates up to
${10}^4\;\mathrm{Gy}\;{\mathrm{s}}^{-1}$
. The effect is attributed to the temporary dead time of the scintillator due to the material’s response time. Favaudon et al. [
Reference Favaudon, Lentz, Heinrich, Patriarca, de Marzi, Fouillade and Dutreix42], on the other hand, have shown linearity for ultra-high dose rate electron irradiation of a gadolinium-based scintillator for dose rates up to
![]() ${10}^4\;\mathrm{Gy}\;{\mathrm{s}}^{-1}$
. The ultra-high dose rate was achieved by
${10}^4\;\mathrm{Gy}\;{\mathrm{s}}^{-1}$
. The ultra-high dose rate was achieved by
![]() $\unicode{x3bc}$
s pulses delivering up to approximately 1 Gy doses in both cases. Our data, in contrast to Ref. [Reference Di Martino, Barca, Barone, Bortoli, Borgheresi, De Stefano, Di Francesco, Faillace, Giuliano, Grasso, Linsalata, Marfisi, Migliorati, Pacitti, Palumbo and Felici41], do not indicate a direct dose-related saturation behaviour, as the overall output signal of the miniSCIDOM scales as predicted by the ToF measurements with a deviation from linearity of less than 10%.
$\unicode{x3bc}$
s pulses delivering up to approximately 1 Gy doses in both cases. Our data, in contrast to Ref. [Reference Di Martino, Barca, Barone, Bortoli, Borgheresi, De Stefano, Di Francesco, Faillace, Giuliano, Grasso, Linsalata, Marfisi, Migliorati, Pacitti, Palumbo and Felici41], do not indicate a direct dose-related saturation behaviour, as the overall output signal of the miniSCIDOM scales as predicted by the ToF measurements with a deviation from linearity of less than 10%.
An effect also discussed in the context of ultra-high dose rates is whether the ultra-high instantaneous flux of protons through the scintillator can lead to an overlap of neighbouring proton tracks. A proton track is here defined as the volume around a single proton path in which the dose is deposited via secondary electrons. The consequences of track overlap include firstly a change in local LET compared to the prediction for a single proton. Secondly, the assumption of independent particles as underlying the MC simulations employed to predict the LET would not be valid anymore. The proton distance for the miniSCIDOM irradiation with LPA protons is estimated based on the depth-resolved proton current (Figure 6(c)) and the scintillator’s response time of
![]() ${t}_{\mathrm{resp}}=$
2.5 ns with the following relation:
${t}_{\mathrm{resp}}=$
2.5 ns with the following relation:
 $$\begin{align}d=\frac{1}{\sqrt{I\cdot {t}_{\mathrm{resp}}}},\end{align}$$
$$\begin{align}d=\frac{1}{\sqrt{I\cdot {t}_{\mathrm{resp}}}},\end{align}$$
yielding 1.3
![]() $\unicode{x3bc}$
m. In comparison to this value, the mean range of secondary electrons amounts to 20 nm in water[
Reference Plante and Cucinotta43] for a mean electron energy of 55 eV[
Reference Vera, Abril and Garcia-Molina44] as expected independently of the proton incident energy for energies of 50–300 MeV. The maximum kinetic energy transfer from protons to electrons can be calculated by the following relation:
$\unicode{x3bc}$
m. In comparison to this value, the mean range of secondary electrons amounts to 20 nm in water[
Reference Plante and Cucinotta43] for a mean electron energy of 55 eV[
Reference Vera, Abril and Garcia-Molina44] as expected independently of the proton incident energy for energies of 50–300 MeV. The maximum kinetic energy transfer from protons to electrons can be calculated by the following relation:
 $$\begin{align}{E}_{\mathrm{trans},{\max}}=\frac{2{m}_{\mathrm{e}}{c}^2\beta }{1-{\beta}^2},\end{align}$$
$$\begin{align}{E}_{\mathrm{trans},{\max}}=\frac{2{m}_{\mathrm{e}}{c}^2\beta }{1-{\beta}^2},\end{align}$$
with the electron rest mass
![]() ${m}_{\mathrm{e}}$
, speed of light
${m}_{\mathrm{e}}$
, speed of light
![]() $c$
and the
$c$
and the
![]() $\beta$
factor. Equation (3) yields 52 keV for a proton energy of 24 MeV (
$\beta$
factor. Equation (3) yields 52 keV for a proton energy of 24 MeV (
![]() $\beta$
= 0.22), that is, close to the spectral peak of the proton bunch (Figure 5(b)). The according electron range is 4.7
$\beta$
= 0.22), that is, close to the spectral peak of the proton bunch (Figure 5(b)). The according electron range is 4.7
![]() $\unicode{x3bc}$
m, making proton track interaction in principle possible. Even so, the dose deposited approximately
$\unicode{x3bc}$
m, making proton track interaction in principle possible. Even so, the dose deposited approximately
![]() $\unicode{x3bc}$
m away from the proton track is reduced by orders of magnitude compared to the track centre[
Reference Ogawa, Hirata, Matsuya and Kai45]. For this reason, we believe that dedicated MC simulations are required to investigate the role of track overlap either on actual local LET or MC simulation-based LET prediction in more detail, as, for example, performed by Kreipl et al. [
Reference Kreipl, Friedland and Paretzke46].
$\unicode{x3bc}$
m away from the proton track is reduced by orders of magnitude compared to the track centre[
Reference Ogawa, Hirata, Matsuya and Kai45]. For this reason, we believe that dedicated MC simulations are required to investigate the role of track overlap either on actual local LET or MC simulation-based LET prediction in more detail, as, for example, performed by Kreipl et al. [
Reference Kreipl, Friedland and Paretzke46].
In summary, at this point we cannot explain the experimental observation on altered ionization quenching behaviour at an LPA proton source. However, we hope that the high interest in ultra-high dose rate radiation characterization (from, e.g., the LPA source and FLASH community) will generate further data and hence insight in the near future.
6. Conclusions
The miniSCIDOM detector fulfils the diagnostic requirements arising when employing LPA proton sources for radiobiological studies, that is, a sub-mm spatial resolution for volumetric dose distributions up to approximately 1 cm
![]() ${}^3$
with a lower detection limit of 100 mGy with a sensitivity for single proton bunches. The realization of tomographic reconstruction via a single objective makes the setup robust and easy to align in any experiment. A point that could require further optimization is the treatment of the scintillator surfaces, that is, either roughening or polishing, to minimize the generation of background radiation through reflections.
${}^3$
with a lower detection limit of 100 mGy with a sensitivity for single proton bunches. The realization of tomographic reconstruction via a single objective makes the setup robust and easy to align in any experiment. A point that could require further optimization is the treatment of the scintillator surfaces, that is, either roughening or polishing, to minimize the generation of background radiation through reflections.
With the measured data indicating a linearity of dose deposition in the scintillator and light output, calibration of the device to provide dose values is in principle possible. Furthermore, the observed deviation from expected ionization quenching behaviour suggests the miniSCIDOM as a platform to study ultra-high dose rate effects in plastic scintillators.
Acknowledgements
We gratefully acknowledge the DRACO laser team and UPTD team for excellent experiment support. The work was partially supported by H2020 Laserlab Europe V (PRISES, Contract No. 871124) and by the European Union’s Horizon 2020 Research and Innovation Programme Impulse (Grant agreement No. 871161). We recognize the support of the Weizmann-Helmholtz Laboratory for Laser Matter Interaction (WHELMI).