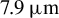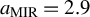1 Introduction
Over the past few decades, laser pulses have been widely used in fundamental science, industry, medicine and so on. In particular, the laser–matter interaction has entered into the relativistic regime due to the invention of the chirped pulse amplification (CPA) technique[
Reference Strickland and Mourou
1
]. Currently, the theoretical and experimental studies in this regime have mainly used Ti:sapphire and Nd:glass laser pulses with wavelengths of 0.8 or
![]() $1.0\;\unicode{x3bc} \mathrm{m}$
[
Reference An, Chi, Dang, Fu, Guo, Huang, He, Kong, Lan, Li, Liu, Shi, Sun, Wang, Wang, Wang, Wei, Wu, Xu, Xi, Yang, Zhang, Zhang, Zheng, Zhang and Zhang
2
–
Reference Hu, Zhao, Zhang, Lu, Wang, Hu, Shao and Yu
6
]. However, pulses in other wavelength bands, such as mid-infrared (mid-IR), are attracting increasing interest due to many applications, such as 2D infrared spectroscopy[
Reference Calabrese, Stingel, Shen and Petersen
7
] and time-resolved imaging of molecular structures[
Reference Blaga, Xu, DiChiara, Sistrunk, Zhang, Agostini, Miller, DiMauro and Lin
8
]. On the other hand, when the mid-IR pulse is enhanced to relativistic intensity, it can also be widely used in the laser interaction with matter, such as in the detection of electron energy[
Reference Wolter, Pullen, Baudisch, Sclafani, Hemmer, Senftleben, Schröter, Ullrich, Moshammer and Biegert
9
], terahertz (THz) emission[
Reference Wang, Kawata, Sheng, Li, Chen, Qian and Zhang
10
], high-order harmonic generation (HHG)[
Reference Popmintchev, Chen, Popmintchev, Arpin, Brown, Ališauskas, Andriukaitis, Balčiunas, Mücke, Pugzlys, Baltuška, Shim, Schrauth, Gaeta, Hernández-García, Plaja, Becker, Jaron-Becker, Murnane and Kapteyn
11
,
Reference Weisshaupt, Juvé, Holtz, Ku, Woerner, Elsaesser, Ališauskas, Pugžlys and Baltuška
12
] and charged particle acceleration[
Reference Pogorelsky, Polyanskiy and Kimura
13
–
Reference Zhang, Hafz, Ma, Qian, Shao and Sheng
15
], all of which would benefit from the long carrier wavelength, few-cycle duration and high peak intensity of the mid-IR pulse. To date, high-intensity mid-IR pulses have been achieved via traditional nonlinear optical methods, for example, optical parametric amplification[
Reference Chen, Wittmann, Morimoto, Baum and Riedle
16
,
Reference Elu, Baudisch, Pires, Tani, Frosz, Köttig, Ermolov, Russell and Biegert
17
], difference frequency generation[
Reference Pupeza, Sánchez, Zhang, Lilienfein, Seidel, Karpowicz, Paasch-Colberg, Znakovskaya, Pescher, Schweinberger, Pervak, Fill, Pronin, Wei, Krausz, Apolonski and Biegert
18
,
Reference Krogen, Suchowski, Liang, Flemens, Hong, Kärtner and Moses
19
], four-wave mixing[
Reference Pigeon, Tochitsky, Welch and Joshi
20
] and optical rectification[
Reference Junginger, Sell, Schubert, Mayer, Brida, Marangoni, Cerullo, Leitenstorfer and Huber
21
,
Reference Pigeon, Tochitsky, Gong and Joshi
22
]. Moreover, the
$1.0\;\unicode{x3bc} \mathrm{m}$
[
Reference An, Chi, Dang, Fu, Guo, Huang, He, Kong, Lan, Li, Liu, Shi, Sun, Wang, Wang, Wang, Wei, Wu, Xu, Xi, Yang, Zhang, Zhang, Zheng, Zhang and Zhang
2
–
Reference Hu, Zhao, Zhang, Lu, Wang, Hu, Shao and Yu
6
]. However, pulses in other wavelength bands, such as mid-infrared (mid-IR), are attracting increasing interest due to many applications, such as 2D infrared spectroscopy[
Reference Calabrese, Stingel, Shen and Petersen
7
] and time-resolved imaging of molecular structures[
Reference Blaga, Xu, DiChiara, Sistrunk, Zhang, Agostini, Miller, DiMauro and Lin
8
]. On the other hand, when the mid-IR pulse is enhanced to relativistic intensity, it can also be widely used in the laser interaction with matter, such as in the detection of electron energy[
Reference Wolter, Pullen, Baudisch, Sclafani, Hemmer, Senftleben, Schröter, Ullrich, Moshammer and Biegert
9
], terahertz (THz) emission[
Reference Wang, Kawata, Sheng, Li, Chen, Qian and Zhang
10
], high-order harmonic generation (HHG)[
Reference Popmintchev, Chen, Popmintchev, Arpin, Brown, Ališauskas, Andriukaitis, Balčiunas, Mücke, Pugzlys, Baltuška, Shim, Schrauth, Gaeta, Hernández-García, Plaja, Becker, Jaron-Becker, Murnane and Kapteyn
11
,
Reference Weisshaupt, Juvé, Holtz, Ku, Woerner, Elsaesser, Ališauskas, Pugžlys and Baltuška
12
] and charged particle acceleration[
Reference Pogorelsky, Polyanskiy and Kimura
13
–
Reference Zhang, Hafz, Ma, Qian, Shao and Sheng
15
], all of which would benefit from the long carrier wavelength, few-cycle duration and high peak intensity of the mid-IR pulse. To date, high-intensity mid-IR pulses have been achieved via traditional nonlinear optical methods, for example, optical parametric amplification[
Reference Chen, Wittmann, Morimoto, Baum and Riedle
16
,
Reference Elu, Baudisch, Pires, Tani, Frosz, Köttig, Ermolov, Russell and Biegert
17
], difference frequency generation[
Reference Pupeza, Sánchez, Zhang, Lilienfein, Seidel, Karpowicz, Paasch-Colberg, Znakovskaya, Pescher, Schweinberger, Pervak, Fill, Pronin, Wei, Krausz, Apolonski and Biegert
18
,
Reference Krogen, Suchowski, Liang, Flemens, Hong, Kärtner and Moses
19
], four-wave mixing[
Reference Pigeon, Tochitsky, Welch and Joshi
20
] and optical rectification[
Reference Junginger, Sell, Schubert, Mayer, Brida, Marangoni, Cerullo, Leitenstorfer and Huber
21
,
Reference Pigeon, Tochitsky, Gong and Joshi
22
]. Moreover, the
![]() ${\mathrm{CO}}_2$
laser obtained in a gas medium is also an important source of the high-intensity mid-IR pulse[
Reference Haberberger, Tochitsky and Joshi
23
,
Reference Polyanskiy, Pogorelsky and Yakimenko
24
]. However, due to the damage threshold of the optical crystal, it is still challenging to generate mid-IR pulses with relativistic intensity, few cycles and controllable carrier wavelengths. In recent years, plasma-based optical modulation has received significant attention, and several effective schemes have been proposed to obtain high-intensity mid-IR pulses, such as the plasma optical modulator[
Reference Yu, Zhao, Qian, Chen, Weng, Sheng, Jaroszynski, Mori and Zhang
25
], synchrotron radiation of refluxing electrons[
Reference Qu, Liu, Liu, Gray, McKenna, Li, Kawata and Kong
26
], laser filamentation[
Reference Mitrofanov, Voronin, Sidorov-Biryukov, Mitryukovsky, Fedotov, Serebryannikov, Meshchankin, Shumakova, Ališauskas, Pugžlys, Panchenko, Baltuška and Zheltikov
27
] and photon deceleration[
Reference Pai, Chang, Ha, Xie, Lin, Lin, Chen, Tsaur, Chu, Chen, Lin, Wang and Chen
28
–
Reference Zhu, Liu, Weng, Chen, Sheng and Zhang
34
]. Among them, photon deceleration is the most feasible and experimentally validated method. In general, when a relativistic intensity laser propagates in an underdense plasma, a strong plasma wave or nonlinear laser wakefield can be excited by the laser ponderomotive force. In the highly nonlinear regime or the bubble regime of the laser wakefield excitation, the photon frequency can be decreased or increased due to the effect of the refractive index gradient (
${\mathrm{CO}}_2$
laser obtained in a gas medium is also an important source of the high-intensity mid-IR pulse[
Reference Haberberger, Tochitsky and Joshi
23
,
Reference Polyanskiy, Pogorelsky and Yakimenko
24
]. However, due to the damage threshold of the optical crystal, it is still challenging to generate mid-IR pulses with relativistic intensity, few cycles and controllable carrier wavelengths. In recent years, plasma-based optical modulation has received significant attention, and several effective schemes have been proposed to obtain high-intensity mid-IR pulses, such as the plasma optical modulator[
Reference Yu, Zhao, Qian, Chen, Weng, Sheng, Jaroszynski, Mori and Zhang
25
], synchrotron radiation of refluxing electrons[
Reference Qu, Liu, Liu, Gray, McKenna, Li, Kawata and Kong
26
], laser filamentation[
Reference Mitrofanov, Voronin, Sidorov-Biryukov, Mitryukovsky, Fedotov, Serebryannikov, Meshchankin, Shumakova, Ališauskas, Pugžlys, Panchenko, Baltuška and Zheltikov
27
] and photon deceleration[
Reference Pai, Chang, Ha, Xie, Lin, Lin, Chen, Tsaur, Chu, Chen, Lin, Wang and Chen
28
–
Reference Zhu, Liu, Weng, Chen, Sheng and Zhang
34
]. Among them, photon deceleration is the most feasible and experimentally validated method. In general, when a relativistic intensity laser propagates in an underdense plasma, a strong plasma wave or nonlinear laser wakefield can be excited by the laser ponderomotive force. In the highly nonlinear regime or the bubble regime of the laser wakefield excitation, the photon frequency can be decreased or increased due to the effect of the refractive index gradient (
![]() $\partial \eta /\partial \xi$
) in different laser-rest frame positions, where
$\partial \eta /\partial \xi$
) in different laser-rest frame positions, where
![]() $\eta$
is the refractive index and
$\eta$
is the refractive index and
![]() $\xi =x- ct$
is the co-moving coordinate of the laser. Specifically, the photon frequency will be downshifted (red-shifted) corresponding to a refractive index gradient less than zero (
$\xi =x- ct$
is the co-moving coordinate of the laser. Specifically, the photon frequency will be downshifted (red-shifted) corresponding to a refractive index gradient less than zero (
![]() $\partial \eta /\partial \xi <0$
), that is, so-called ‘photon deceleration’, while the photon frequency will be upshifted (blue-shifted) corresponding to a refractive index gradient larger than zero (
$\partial \eta /\partial \xi <0$
), that is, so-called ‘photon deceleration’, while the photon frequency will be upshifted (blue-shifted) corresponding to a refractive index gradient larger than zero (
![]() $\partial \eta /\partial \xi >0$
)[
Reference Pai, Chang, Ha, Xie, Lin, Lin, Chen, Tsaur, Chu, Chen, Lin, Wang and Chen
28
,
Reference Wilks, Dawson, Mori, Katsouleas and Jones
35
–
Reference Zhu, Palastro and Antonsen
38
]. The fundamental physics of the photon deceleration is the coupling of the self-phase modulation (SPM) and group velocity dispersion (GVD), which makes part of the drive laser frequency downshift. Then, the resulting long-wavelength mid-IR pulse slips rapidly backwards into the bubble. Recently, a relativistic single-cycle mid-IR pulse has been generated by using a tailored plasma density structure[
Reference Nie, Pai, Hua, Zhang, Wu, Wan, Li, Zhang, Cheng, Su, Liu, Ma, Ning, He, Lu, Chu, Wang, Mori and Joshi
29
], which has already been demonstrated experimentally[
Reference Nie, Pai, Zhang, Ning, Hua, He, Wu, Su, Liu, Ma, Cheng, Lu, Chu, Wang, Zhang, Mori and Joshi
30
]. However, the positions of the convertor and coupler modules are difficult to control in these schemes, and these schemes require a long gas length for pulse compression, which may decrease the energy of the drive laser. In order to improve the efficiency of the laser energy conversion to the mid-IR pulse, a new method by using two co-propagating laser pulses (a drive light and a signal light) is proposed[
Reference Zhu, Weng, Chen, Sheng and Zhang
31
], but the mid-IR pulse wavelength is limited to
$\partial \eta /\partial \xi >0$
)[
Reference Pai, Chang, Ha, Xie, Lin, Lin, Chen, Tsaur, Chu, Chen, Lin, Wang and Chen
28
,
Reference Wilks, Dawson, Mori, Katsouleas and Jones
35
–
Reference Zhu, Palastro and Antonsen
38
]. The fundamental physics of the photon deceleration is the coupling of the self-phase modulation (SPM) and group velocity dispersion (GVD), which makes part of the drive laser frequency downshift. Then, the resulting long-wavelength mid-IR pulse slips rapidly backwards into the bubble. Recently, a relativistic single-cycle mid-IR pulse has been generated by using a tailored plasma density structure[
Reference Nie, Pai, Hua, Zhang, Wu, Wan, Li, Zhang, Cheng, Su, Liu, Ma, Ning, He, Lu, Chu, Wang, Mori and Joshi
29
], which has already been demonstrated experimentally[
Reference Nie, Pai, Zhang, Ning, Hua, He, Wu, Su, Liu, Ma, Cheng, Lu, Chu, Wang, Zhang, Mori and Joshi
30
]. However, the positions of the convertor and coupler modules are difficult to control in these schemes, and these schemes require a long gas length for pulse compression, which may decrease the energy of the drive laser. In order to improve the efficiency of the laser energy conversion to the mid-IR pulse, a new method by using two co-propagating laser pulses (a drive light and a signal light) is proposed[
Reference Zhu, Weng, Chen, Sheng and Zhang
31
], but the mid-IR pulse wavelength is limited to
![]() $5\;\unicode{x3bc} \mathrm{m}$
. Therefore, more feasible and efficient schemes for generating relativistic intensity, few-cycle and long-wavelength controllable mid-IR pulses are in high demand both in theory and experiments.
$5\;\unicode{x3bc} \mathrm{m}$
. Therefore, more feasible and efficient schemes for generating relativistic intensity, few-cycle and long-wavelength controllable mid-IR pulses are in high demand both in theory and experiments.
Frequency chirp widely exists in femtosecond (fs) lasers, which can be produced easily by adjusting the grating spacing of the compressor in experiments. Chirped laser pulses (CLPs) have also been widely applied in laser–plasma interaction, such as improving the quality of electron beams[
Reference Pathak, Vieira, Fonseca and Silva
39
–
Reference Rezaei-Pandari, Niknam, Massudi, Jahangiri, Hassaninejad and Khorashadizadeh
42
], enhancing the radiation intensity of THz emission[
Reference Wang, Sheng, Wu, Chen, Li, Zhang and Mima
43
–
Reference Gurjar, Gopal, Gupta, Kulagin and Suk
45
] and HHG[
Reference Kim and Nam
46
,
Reference Neyra, Videla, Pérez-Hernández, Ciappina, Roso and Torchia
47
]. In the nonlinear case, compared with un-chirped laser pulses, the negatively chirped laser pulses (NCLPs) are compressed longitudinally in plasma, while the positively chirped laser pulses (PCLPs) can be stretched[
Reference Zhang, Shen, Ji, Wang, Xu, Yu, Yi, Wang, Hafz and Kulagin
40
]. However, the evolution of density perturbation at the position of the CLP and its subsequent effect on the refractive index are not considered. In particular, the compression of the NCLP can enhance the intensity of drive laser pulses and the perturbation of plasma density. This characteristic can be used effectively to control the generation of long-wavelength mid-IR pulses by photon deceleration. According to the dispersion relation of laser pulses,
![]() ${\omega}^2={c}^2{k}^2+{\omega}_{\mathrm{p}}^2$
, the refractive index is a function of laser frequency and plasma frequency, which makes the refractive index change with the frequency distribution of the NCLP and the PCLP. Therefore, the generation process of mid-IR pulses can be hopefully controlled.
${\omega}^2={c}^2{k}^2+{\omega}_{\mathrm{p}}^2$
, the refractive index is a function of laser frequency and plasma frequency, which makes the refractive index change with the frequency distribution of the NCLP and the PCLP. Therefore, the generation process of mid-IR pulses can be hopefully controlled.
Here, in order to improve the generation of a relativistic intensity, few-cycle, long carrier wavelength mid-IR pulse, we propose a scheme to effectively enhance the mid-IR pulse generation efficiency by controlling the chirp parameters of the NCLP. Due to the difference of phase velocity and group velocity of different frequency components of the NCLP, the NCLP is rapidly compressed longitudinally, which increases the intensity of the drive laser and plasma density perturbation. More pulse components can thus enter into the photon deceleration region, where the refractive index gradient is negative, that is,
![]() $\partial \eta /\partial \xi <0$
. The mid-IR pulse is thus produced faster and the corresponding energy conversion efficiency becomes higher. Meanwhile, the quality of the mid-IR pulse can be controlled by changing the chirp parameters. The carrier-envelope phase (CEP) of the mid-IR pulse is also phase-locked with the central phase of the initial NCLP. Such a straight and efficient mid-IR source with relativistic intensity, few cycles and controllable wavelength can find a variety of scientific applications in many domains.
$\partial \eta /\partial \xi <0$
. The mid-IR pulse is thus produced faster and the corresponding energy conversion efficiency becomes higher. Meanwhile, the quality of the mid-IR pulse can be controlled by changing the chirp parameters. The carrier-envelope phase (CEP) of the mid-IR pulse is also phase-locked with the central phase of the initial NCLP. Such a straight and efficient mid-IR source with relativistic intensity, few cycles and controllable wavelength can find a variety of scientific applications in many domains.
2 Mode and scheme
The schematic diagram of the scheme is shown in Figure 1. The projections at the bottom represent the profile of the plasma. In the scheme, the generation of a mid-IR pulse by the NCLP, that is, the high-frequency component first and low-frequency second, can be divided into three stages: (I) the wakefield excitation stage; (II) the electron layer compression stage; and (III) the pulse converter stage. In stage (I), the NCLP excites a bubble to move forward at the group velocity of the drive laser pulse. At the same time, each frequency component of the NCLP produces a special curving profile of the refractive index, as shown by the green curve, and the photons in the range of
![]() $\partial \eta /\partial \xi <0$
move backward and others in the range of
$\partial \eta /\partial \xi <0$
move backward and others in the range of
![]() $\partial \eta /\partial \xi >0$
move forward, as directed by the blue arrows, which together with the plasma etching lead to the rapid compression of the NCLP in the longitudinal direction. Finally, the pulse width becomes shorter and the laser peak intensity increases dramatically after propagation of a few Rayleigh lengths at stage (II), so that the compressed pulse enters the mid-IR converter stage. At this point, stage (III), the photons are rapidly decelerated due to the greater negative refractive index gradient, and then the generated mid-IR pulse slips backward into the bubble and propagates forward together with the bubble.
$\partial \eta /\partial \xi >0$
move forward, as directed by the blue arrows, which together with the plasma etching lead to the rapid compression of the NCLP in the longitudinal direction. Finally, the pulse width becomes shorter and the laser peak intensity increases dramatically after propagation of a few Rayleigh lengths at stage (II), so that the compressed pulse enters the mid-IR converter stage. At this point, stage (III), the photons are rapidly decelerated due to the greater negative refractive index gradient, and then the generated mid-IR pulse slips backward into the bubble and propagates forward together with the bubble.

Figure 1 Schematic of laser chirp controlled few-cycle mid-IR pulse generation. Due to the special curving profile of the refractive index of the NCLP and the plasma etching, the pulse is rapidly compressed longitudinally. As a result, a large number of photons approach the photon deceleration phase, and produce the mid-infrared frequency component, which then slips backwards into the bubble and moves forward together with the bubble. The red curves represent the distribution of the laser electric field on-axis, and the green curves represent the corresponding distribution of the refractive index of the NCLP. The blue arrows denote the photon emission directions relative to the bubble.
Photon deceleration is caused essentially by plasma optical modulation. The basic physics of mid-IR generation in plasma by the NCLP can be interpreted by 1D nonlinear theory[ Reference Nie, Pai, Hua, Zhang, Wu, Wan, Li, Zhang, Cheng, Su, Liu, Ma, Ning, He, Lu, Chu, Wang, Mori and Joshi 29 ]. The electric field of a CLP with the polarization along the y-direction that propagates along the x-direction can be expressed as follows:
 $$ \begin{align}{E}_{\mathrm{L}}(t)={E}_{\mathrm{L}0}\exp \left(-\frac{r^2}{w_0^2}\right){\sin}^2\left(\frac{\pi t}{\tau_{\mathrm{d}}}\right)\sin \left[\omega (t)t\right],\end{align}$$
$$ \begin{align}{E}_{\mathrm{L}}(t)={E}_{\mathrm{L}0}\exp \left(-\frac{r^2}{w_0^2}\right){\sin}^2\left(\frac{\pi t}{\tau_{\mathrm{d}}}\right)\sin \left[\omega (t)t\right],\end{align}$$
where
![]() ${E}_{\mathrm{L}0}$
is the initial peak electric field,
${E}_{\mathrm{L}0}$
is the initial peak electric field,
![]() ${w}_0$
is the spot size and
${w}_0$
is the spot size and
![]() ${\tau}_{\mathrm{d}}$
is the full length of the laser pulse. Here,
${\tau}_{\mathrm{d}}$
is the full length of the laser pulse. Here,
![]() ${\omega (t)={\omega}_0\left[1-b\left(t/{T}_0-{t}_{\mathrm{c}}/{T}_0\right)\right]}$
is the local longitudinal frequency of a linearly CLP, where
${\omega (t)={\omega}_0\left[1-b\left(t/{T}_0-{t}_{\mathrm{c}}/{T}_0\right)\right]}$
is the local longitudinal frequency of a linearly CLP, where
![]() ${\omega}_0=2\pi c/{\lambda}_0$
is the center angular frequency,
${\omega}_0=2\pi c/{\lambda}_0$
is the center angular frequency,
![]() ${\lambda}_0$
is the center wavelength of the CLP,
${\lambda}_0$
is the center wavelength of the CLP,
![]() $c$
is the speed of light in a vacuum,
$c$
is the speed of light in a vacuum,
![]() ${T}_0$
is the laser period,
${T}_0$
is the laser period,
![]() ${t}_{\mathrm{c}}={\tau}_{\mathrm{d}}/2$
is the initial center of the laser pulse and
${t}_{\mathrm{c}}={\tau}_{\mathrm{d}}/2$
is the initial center of the laser pulse and
![]() $b$
is the linear chirp parameter. Here, we assume
$b$
is the linear chirp parameter. Here, we assume
![]() $b>0$
for a PCLP and
$b>0$
for a PCLP and
![]() $b<0$
for an NCLP.
$b<0$
for an NCLP.
The interaction of relativistic CLPs with underdense plasma can be described by the coupled equations under the Coulomb gauge[ Reference Zhang, Shen, Ji, Wang, Xu, Yu, Yi, Wang, Hafz and Kulagin 40 , Reference Afhami and Eslami 41 , Reference Sprangle, Esarey and Ting 48 – Reference Khachatryan, van Goor and Boller 51 ]:
 $$\begin{align}\left(2c\frac{\partial^2a}{\partial \xi \partial \tau }-\frac{\partial^2a}{\partial {\tau}^2}\right)={c}^2{k}_{\mathrm{p}}^2\frac{a}{1+\phi },\end{align}$$
$$\begin{align}\left(2c\frac{\partial^2a}{\partial \xi \partial \tau }-\frac{\partial^2a}{\partial {\tau}^2}\right)={c}^2{k}_{\mathrm{p}}^2\frac{a}{1+\phi },\end{align}$$
 $$\begin{align}2\frac{\partial^2\phi }{\partial {\xi}^2}={k}_{\mathrm{p}}^2\left[\frac{1+{p}_y^2}{{\left(1+\phi \right)}^2}-1\right],\end{align}$$
$$\begin{align}2\frac{\partial^2\phi }{\partial {\xi}^2}={k}_{\mathrm{p}}^2\left[\frac{1+{p}_y^2}{{\left(1+\phi \right)}^2}-1\right],\end{align}$$
where
![]() ${a}\left(\xi \right)=\left[e{A}\left(\xi \right)\right]/\left({m}_{\mathrm{e}}{c}^2\right)$
and
${a}\left(\xi \right)=\left[e{A}\left(\xi \right)\right]/\left({m}_{\mathrm{e}}{c}^2\right)$
and
![]() $\phi \left(\xi \right)=\left[e\Phi \left(\xi \right)\right]/\left({m}_{\mathrm{e}}{c}^2\right)$
are the normalized vector and scalar potentials associated with the laser pulse and the wakefield, respectively. Here,
$\phi \left(\xi \right)=\left[e\Phi \left(\xi \right)\right]/\left({m}_{\mathrm{e}}{c}^2\right)$
are the normalized vector and scalar potentials associated with the laser pulse and the wakefield, respectively. Here,
![]() $\xi =x- ct$
and
$\xi =x- ct$
and
![]() $\tau =t$
are in the laser-rest frame,
$\tau =t$
are in the laser-rest frame,
![]() ${k}_{\mathrm{p}}={\omega}_{\mathrm{p}}/c$
is the plasma wave number,
${k}_{\mathrm{p}}={\omega}_{\mathrm{p}}/c$
is the plasma wave number,
![]() ${\omega}_{\mathrm{p}}=\sqrt{\left(4\pi {n}_{\mathrm{e}}{e}^2\right)/{m}_{\mathrm{e}}}$
is the plasma frequency,
${\omega}_{\mathrm{p}}=\sqrt{\left(4\pi {n}_{\mathrm{e}}{e}^2\right)/{m}_{\mathrm{e}}}$
is the plasma frequency,
![]() $c$
is the speed of light in a vacuum,
$c$
is the speed of light in a vacuum,
![]() $e$
is the unit charge,
$e$
is the unit charge,
![]() ${n}_{\mathrm{e}}$
is the plasma density and
${n}_{\mathrm{e}}$
is the plasma density and
![]() ${m}_{\mathrm{e}}$
is the electron mass. Equation (3) can be solved numerically by the fourth-order Runge–Kutta method. In Equation (3),
${m}_{\mathrm{e}}$
is the electron mass. Equation (3) can be solved numerically by the fourth-order Runge–Kutta method. In Equation (3),
![]() ${p}_y={p}_{y0}+A$
is the transverse momentum component of electrons and
${p}_y={p}_{y0}+A$
is the transverse momentum component of electrons and
![]() $A$
is defined as
$A$
is defined as
![]() $A\sim {\int}_{\xi_0}^{\xi }{E}_{\mathrm{L}}\left({\xi}^{\prime}\right)\kern0.1em \mathrm{d}{\xi}^{\prime }$
, where
$A\sim {\int}_{\xi_0}^{\xi }{E}_{\mathrm{L}}\left({\xi}^{\prime}\right)\kern0.1em \mathrm{d}{\xi}^{\prime }$
, where
![]() ${\xi_0=\xi \left(\tau =0\right)}$
and
${\xi_0=\xi \left(\tau =0\right)}$
and
![]() ${p}_{y0}$
are the initial position and momentum of the plasma electron, respectively. Considering a cold plasma,
${p}_{y0}$
are the initial position and momentum of the plasma electron, respectively. Considering a cold plasma,
![]() ${p}_{y0}=0$
, the transverse momentum completely depends on the laser pulse. Compared with the un-chirped laser pulse, electrons driven by a CLP can still have a nonzero transverse momentum, which is constant behind the pulse.
${p}_{y0}=0$
, the transverse momentum completely depends on the laser pulse. Compared with the un-chirped laser pulse, electrons driven by a CLP can still have a nonzero transverse momentum, which is constant behind the pulse.
From Equation (2), we can get the refractive index of a CLP as follows:
 $$\begin{align}\eta \left(\tau \right)\simeq 1-\frac{\omega_{\mathrm{p}}^2}{2{\omega}^2\left(\tau \right)}\frac{1}{1+\phi},\quad 0<\tau <{\tau}_{\mathrm{d}}.\end{align}$$
$$\begin{align}\eta \left(\tau \right)\simeq 1-\frac{\omega_{\mathrm{p}}^2}{2{\omega}^2\left(\tau \right)}\frac{1}{1+\phi},\quad 0<\tau <{\tau}_{\mathrm{d}}.\end{align}$$
Therefore, the phase velocity and the group velocity can be expressed as
![]() ${v}_{\mathrm{p}}\left(\tau \right)\simeq c\left\{1+\left[{\omega}_{\mathrm{p}}^2/2{\omega}^2\left(\tau \right)\right]\left[1/\left(1+\phi \right)\right]\right\}$
and
${v}_{\mathrm{p}}\left(\tau \right)\simeq c\left\{1+\left[{\omega}_{\mathrm{p}}^2/2{\omega}^2\left(\tau \right)\right]\left[1/\left(1+\phi \right)\right]\right\}$
and
![]() ${v}_{\mathrm{g}}\left(\tau \right)\simeq c\left\{1-\left[{\omega}_{\mathrm{p}}^2/2{\omega}^2\left(\tau \right)\right]\left[1/\left(1+\phi \right)\right]\right\}$
, respectively. Here,
${v}_{\mathrm{g}}\left(\tau \right)\simeq c\left\{1-\left[{\omega}_{\mathrm{p}}^2/2{\omega}^2\left(\tau \right)\right]\left[1/\left(1+\phi \right)\right]\right\}$
, respectively. Here,
![]() $\phi$
is the solution of Equation (3).
$\phi$
is the solution of Equation (3).
The wavelength changes of the drive laser in a short time duration
![]() $\Delta \tau$
can be estimated by
$\Delta \tau$
can be estimated by
![]() $\lambda ={\lambda}_0+{\lambda}_0\Delta \tau \partial {v}_{\mathrm{p}}/\partial \xi$
[
Reference Mori
37
], and
$\lambda ={\lambda}_0+{\lambda}_0\Delta \tau \partial {v}_{\mathrm{p}}/\partial \xi$
[
Reference Mori
37
], and
![]() ${\lambda}_0\partial {v}_{\mathrm{p}}/\partial \xi$
is the difference of the phase velocity between the two adjacent crests. Then, using
${\lambda}_0\partial {v}_{\mathrm{p}}/\partial \xi$
is the difference of the phase velocity between the two adjacent crests. Then, using
![]() ${v}_{\mathrm{p}}=c{\eta}^{-1}$
, the change of
${v}_{\mathrm{p}}=c{\eta}^{-1}$
, the change of
![]() $\lambda$
gives the following:
$\lambda$
gives the following:
 $$\begin{align}\lambda ={\lambda}_0\left(1-c{\int}_0^{t_{\mathrm{i}}}{\eta}^{-2}\frac{\partial \eta }{\partial \xi } \mathrm{d}\tau \right),\end{align}$$
$$\begin{align}\lambda ={\lambda}_0\left(1-c{\int}_0^{t_{\mathrm{i}}}{\eta}^{-2}\frac{\partial \eta }{\partial \xi } \mathrm{d}\tau \right),\end{align}$$
where
![]() ${t}_{\mathrm{i}}$
is the interaction time,
${t}_{\mathrm{i}}$
is the interaction time,
![]() $\partial \eta /\partial \xi >0$
implies photon acceleration and
$\partial \eta /\partial \xi >0$
implies photon acceleration and
![]() $\partial \eta /\partial \xi <0$
means photon deceleration.
$\partial \eta /\partial \xi <0$
means photon deceleration.
We assume an average refractive index gradient of
![]() $-\partial \eta /\partial \xi \sim 3\times {10}^{-3}$
μm
$-\partial \eta /\partial \xi \sim 3\times {10}^{-3}$
μm
![]() ${}^{-1}$
for the case presented here when
${}^{-1}$
for the case presented here when
![]() ${a}_0>1$
, and thus the wavelength modulation can be estimated by Equation (5), which is as high as
${a}_0>1$
, and thus the wavelength modulation can be estimated by Equation (5), which is as high as
![]() $10{\lambda}_0$
over an interaction distance of about 3 mm. Due to the longitudinal compression of the NCLP, the drive pulse can excite a larger negative refractive index gradient.
$10{\lambda}_0$
over an interaction distance of about 3 mm. Due to the longitudinal compression of the NCLP, the drive pulse can excite a larger negative refractive index gradient.
3 Relativistic mid-infrared pulse generation
For the quantitative description for the generation of mid-IR pulses by NCLP interaction with underdense plasma, we first perform a series of 2D particle-in-cell (PIC) simulations by using the open source PIC code EPOCH[
Reference Arber, Bennett, Brady, Lawrence-Douglas, Ramsay, Sircombe, Gillies, Evans, Schmitz, Bell and Ridgers
52
]. The normalized vector potential of the laser pulse is
![]() ${a}_0=2$
, the peak intensity is
${a}_0=2$
, the peak intensity is
![]() ${I}_0=8.6\times {10}^{18}\;\mathrm{W}\;{\mathrm{cm}}^{-2}$
and the center wavelength of the CLPs is
${I}_0=8.6\times {10}^{18}\;\mathrm{W}\;{\mathrm{cm}}^{-2}$
and the center wavelength of the CLPs is
![]() ${\lambda}_0=0.8\;\unicode{x3bc} \mathrm{m}$
, while
${\lambda}_0=0.8\;\unicode{x3bc} \mathrm{m}$
, while
![]() ${w}_0=15\;\unicode{x3bc} \mathrm{m}$
and
${w}_0=15\;\unicode{x3bc} \mathrm{m}$
and
![]() ${{\tau}_{\mathrm{d}}=20{T}_0}$
are the spot size and pulse duration, respectively, where
${{\tau}_{\mathrm{d}}=20{T}_0}$
are the spot size and pulse duration, respectively, where
![]() ${T}_0\approx 2.64$
fs is the laser period. The effective chirp parameter range of the CLP, that is,
${T}_0\approx 2.64$
fs is the laser period. The effective chirp parameter range of the CLP, that is,
![]() $-0.1<b<0.1$
, can be obtained by considering
$-0.1<b<0.1$
, can be obtained by considering
![]() $1-b\left(t/{T}_0-{t}_{\mathrm{c}}/{T}_0\right)>0$
when
$1-b\left(t/{T}_0-{t}_{\mathrm{c}}/{T}_0\right)>0$
when
![]() $0<t<20{T}_0$
and
$0<t<20{T}_0$
and
![]() ${t}_{\mathrm{c}}=10{T}_0$
. The incident laser pulse has a spatial-temporal profile as defined by Equation (1) with the chirp parameter
${t}_{\mathrm{c}}=10{T}_0$
. The incident laser pulse has a spatial-temporal profile as defined by Equation (1) with the chirp parameter
![]() $b=-0.07$
, which corresponds to a pulse energy of about 803 mJ, a full width at half maximum (FWHM) of the spectrum of about 500 nm and a chirp rate of
$b=-0.07$
, which corresponds to a pulse energy of about 803 mJ, a full width at half maximum (FWHM) of the spectrum of about 500 nm and a chirp rate of
![]() $R=W/T\approx 18.9\;\mathrm{nm}/\mathrm{fs}$
[
Reference Brodzik
53
]. Here,
$R=W/T\approx 18.9\;\mathrm{nm}/\mathrm{fs}$
[
Reference Brodzik
53
]. Here,
![]() $W$
is the FWHM of the spectrum and
$W$
is the FWHM of the spectrum and
![]() $T$
is the FWHM of the pulse duration. Such a bandwidth pulse may be achieved by induced-phase modulation (IPM)[
Reference Su, Fang, Gao, Zhao, Chang and Wei
54
] with fused silica plates. A plasma channel is used to guide the propagation of focused laser pulses over many Rayleigh lengths[
Reference Esarey, Schroeder and Leemans
55
] and to excite a stable bubble structure. The simulation box has a total longitudinal length of
$T$
is the FWHM of the pulse duration. Such a bandwidth pulse may be achieved by induced-phase modulation (IPM)[
Reference Su, Fang, Gao, Zhao, Chang and Wei
54
] with fused silica plates. A plasma channel is used to guide the propagation of focused laser pulses over many Rayleigh lengths[
Reference Esarey, Schroeder and Leemans
55
] and to excite a stable bubble structure. The simulation box has a total longitudinal length of
![]() $3500\;\unicode{x3bc} \mathrm{m}$
, and the moving window technology is used. The size of the moving window is
$3500\;\unicode{x3bc} \mathrm{m}$
, and the moving window technology is used. The size of the moving window is
![]() $80\;\unicode{x3bc} \mathrm{m}$
(x)
$80\;\unicode{x3bc} \mathrm{m}$
(x)
![]() $\times$
$\times$
![]() $70\;\unicode{x3bc} \mathrm{m}$
(y) with grid cells of 2400
$70\;\unicode{x3bc} \mathrm{m}$
(y) with grid cells of 2400
![]() $\times$
1400 and 16 macroparticles per cell. The parabolic plasma channel has the transverse density distribution of
$\times$
1400 and 16 macroparticles per cell. The parabolic plasma channel has the transverse density distribution of
![]() ${n}_{\mathrm{e}}={n}_0+\Delta {nr}^2/{w}_0^2$
with a
${n}_{\mathrm{e}}={n}_0+\Delta {nr}^2/{w}_0^2$
with a
![]() $100\;\unicode{x3bc} \mathrm{m}$
up ramp, a
$100\;\unicode{x3bc} \mathrm{m}$
up ramp, a
![]() $3200\;\unicode{x3bc} \mathrm{m}$
plateau and a
$3200\;\unicode{x3bc} \mathrm{m}$
plateau and a
![]() $50\;\unicode{x3bc} \mathrm{m}$
down ramp, where
$50\;\unicode{x3bc} \mathrm{m}$
down ramp, where
![]() ${n}_0=3\times {10}^{18}\;{\mathrm{cm}}^{-3}$
is the background electron density on-axis,
${n}_0=3\times {10}^{18}\;{\mathrm{cm}}^{-3}$
is the background electron density on-axis,
![]() $\Delta n=n\left({w}_0\right)-n(0)=1.13\times {10}^{20}/{w}_0^2\left(\unicode{x3bc} \mathrm{m}\right)$
is the channel depth with the matched laser spot size[
Reference Esarey, Schroeder and Leemans
55
] and
$\Delta n=n\left({w}_0\right)-n(0)=1.13\times {10}^{20}/{w}_0^2\left(\unicode{x3bc} \mathrm{m}\right)$
is the channel depth with the matched laser spot size[
Reference Esarey, Schroeder and Leemans
55
] and
![]() $r$
is the radial distance from the channel axis. This plasma channel can be generated in several ways, which have been widely used in laser–plasma experiments[
Reference Esarey, Schroeder and Leemans
55
–
Reference Mizuta, Hosokai, Masuda, Zhidkov, Makito, Nakanii, Kajino, Nishida, Kando, Mori, Kotaki, Hayashi, Bulanov and Kodama
57
].
$r$
is the radial distance from the channel axis. This plasma channel can be generated in several ways, which have been widely used in laser–plasma experiments[
Reference Esarey, Schroeder and Leemans
55
–
Reference Mizuta, Hosokai, Masuda, Zhidkov, Makito, Nakanii, Kajino, Nishida, Kando, Mori, Kotaki, Hayashi, Bulanov and Kodama
57
].
Figures 2(a)–2(c) show the evolution of the transverse electric field (
![]() ${E}_y$
) of the drive laser and the electron density distribution (
${E}_y$
) of the drive laser and the electron density distribution (
![]() ${n}_{\mathrm{e}}$
), together with longitudinal electron density on-axis. In stage (I), one can see from Figure 2(a) that a stable bubble can be excited, and the laser pulse is located in front of the bubble. The length of the bubble corresponds to the plasma wavelength
${n}_{\mathrm{e}}$
), together with longitudinal electron density on-axis. In stage (I), one can see from Figure 2(a) that a stable bubble can be excited, and the laser pulse is located in front of the bubble. The length of the bubble corresponds to the plasma wavelength
![]() ${\lambda}_{\mathrm{p}}=\left(2\pi c\right)/\sqrt{\left(4\pi {n}_{\mathrm{e}}{e}^2\right)/{m}_{\mathrm{e}}}=19.3\;\unicode{x3bc} \mathrm{m}$
, and the maximum density perturbation is only
${\lambda}_{\mathrm{p}}=\left(2\pi c\right)/\sqrt{\left(4\pi {n}_{\mathrm{e}}{e}^2\right)/{m}_{\mathrm{e}}}=19.3\;\unicode{x3bc} \mathrm{m}$
, and the maximum density perturbation is only
![]() $6\times {10}^{18}\;{\mathrm{cm}}^{-3}$
. Here, the density up ramp of stage (I) can guide the NCLP propagation into the plasma without causing boundary electron injection, and it has almost no effect on the frequency profile of the laser pulses. After that, in stage (II) of Figure 1, the FWHM of the NCLP rapidly compresses to 9 fs when the propagation distance is 1.8 mm, which is well below the initial pulse width, as shown in Figure 2(b). Meanwhile, a small frequency downshift (about
$6\times {10}^{18}\;{\mathrm{cm}}^{-3}$
. Here, the density up ramp of stage (I) can guide the NCLP propagation into the plasma without causing boundary electron injection, and it has almost no effect on the frequency profile of the laser pulses. After that, in stage (II) of Figure 1, the FWHM of the NCLP rapidly compresses to 9 fs when the propagation distance is 1.8 mm, which is well below the initial pulse width, as shown in Figure 2(b). Meanwhile, a small frequency downshift (about
![]() $2\;\unicode{x3bc} \mathrm{m}$
) can be seen, represented by the black curve in Figure 2(e). With the compression of the drive laser in stage (II), the peak electric field of the NCLP can approach
$2\;\unicode{x3bc} \mathrm{m}$
) can be seen, represented by the black curve in Figure 2(e). With the compression of the drive laser in stage (II), the peak electric field of the NCLP can approach
![]() $1.7\times {10}^{13}\;\mathrm{V}\;{\mathrm{m}}^{-1}$
, and the plasma density in front of the bubble is increased in excess of
$1.7\times {10}^{13}\;\mathrm{V}\;{\mathrm{m}}^{-1}$
, and the plasma density in front of the bubble is increased in excess of
![]() $3\times {10}^{19}\;{\mathrm{cm}}^{-3}$
at
$3\times {10}^{19}\;{\mathrm{cm}}^{-3}$
at
![]() $t=2250{T}_0$
. The enhanced density peak provides a large negative refractive index gradient
$t=2250{T}_0$
. The enhanced density peak provides a large negative refractive index gradient
![]() $\partial \eta /\partial \xi$
, as shown in Figure 1, leading to more efficient photon deceleration. For example, at
$\partial \eta /\partial \xi$
, as shown in Figure 1, leading to more efficient photon deceleration. For example, at
![]() $t=2250{T}_0$
, one can estimate
$t=2250{T}_0$
, one can estimate
![]() $\partial \eta /\partial \xi \approx -8\times {10}^{-3}\;{\unicode{x3bc} \mathrm{m}}^{-1}$
. Therefore, compared with the un-chirped pulse, the NCLP can rapidly obtain a large refractive index gradient in a shorter plasma by severe compression. After
$\partial \eta /\partial \xi \approx -8\times {10}^{-3}\;{\unicode{x3bc} \mathrm{m}}^{-1}$
. Therefore, compared with the un-chirped pulse, the NCLP can rapidly obtain a large refractive index gradient in a shorter plasma by severe compression. After
![]() $t=2250{T}_0$
, the pulse enters into stage (III), where the large refractive index gradient leads to a rapid frequency downshift of photons. Assuming the number of photons to be constant, that is, regardless of the energy loss, the frequency downshift of photons will lead to a reduction of the laser pulse energy, which manifests as deceleration. Therefore, the low-frequency mid-IR pulse slips backward, and fills the entire bubble, as shown in Figure 2(c). The on-axis spectral evolution is shown in Figure 2(d), where one can see that the laser experiences a red-shift steadily before the pulse is compressed. Then the photons constantly slow down. As a result, the spectrum shows multiple mid-IR components. Figure 2(e) shows the spectral distributions at different times. A mid-IR pulse is generated with the maximum center wavelength of
$t=2250{T}_0$
, the pulse enters into stage (III), where the large refractive index gradient leads to a rapid frequency downshift of photons. Assuming the number of photons to be constant, that is, regardless of the energy loss, the frequency downshift of photons will lead to a reduction of the laser pulse energy, which manifests as deceleration. Therefore, the low-frequency mid-IR pulse slips backward, and fills the entire bubble, as shown in Figure 2(c). The on-axis spectral evolution is shown in Figure 2(d), where one can see that the laser experiences a red-shift steadily before the pulse is compressed. Then the photons constantly slow down. As a result, the spectrum shows multiple mid-IR components. Figure 2(e) shows the spectral distributions at different times. A mid-IR pulse is generated with the maximum center wavelength of
![]() ${\lambda}_{\mathrm{c}}=7.9\;\unicode{x3bc} \mathrm{m}$
at
${\lambda}_{\mathrm{c}}=7.9\;\unicode{x3bc} \mathrm{m}$
at
![]() $t=3600{T}_0$
. Figure 2(f) shows the temporal profile of the mid-IR pulse at
$t=3600{T}_0$
. Figure 2(f) shows the temporal profile of the mid-IR pulse at
![]() $t=3600{T}_0$
. The temporal FWHM of the mid-IR pulse is approximately 56.8 fs and the number of optical cycles is roughly 2.2. Considering the peak electric field of mid-IR pulses with
$t=3600{T}_0$
. The temporal FWHM of the mid-IR pulse is approximately 56.8 fs and the number of optical cycles is roughly 2.2. Considering the peak electric field of mid-IR pulses with
![]() ${E}_{\mathrm{MIR}}\approx 1.1\times {10}^{12}\;\mathrm{V}\;{\mathrm{m}}^{-1}$
, the normalized pulse intensity can be estimated as
${E}_{\mathrm{MIR}}\approx 1.1\times {10}^{12}\;\mathrm{V}\;{\mathrm{m}}^{-1}$
, the normalized pulse intensity can be estimated as
![]() ${{a}_{\mathrm{MIR}}=\left(e{\lambda}_{\mathrm{c}}{E}_{\mathrm{MIR}}\right)/\left(2\pi {m}_{\mathrm{e}}{c}^2\right)\approx 2.9}$
. Therefore, it is a relativistic, few-cycle and long-wavelength mid-IR pulse.
${{a}_{\mathrm{MIR}}=\left(e{\lambda}_{\mathrm{c}}{E}_{\mathrm{MIR}}\right)/\left(2\pi {m}_{\mathrm{e}}{c}^2\right)\approx 2.9}$
. Therefore, it is a relativistic, few-cycle and long-wavelength mid-IR pulse.

Figure 2 2D simulation of mid-IR generation with the NCLP. (a)–(c) Distributions of the plasma density (
![]() ${n}_{\mathrm{e}}$
) and transverse electric field (
${n}_{\mathrm{e}}$
) and transverse electric field (
![]() ${E}_y$
) at different times. The orange curve is the electron density on-axis. (d) Spectral evolution as a function of the propagation time. (e) Spectral distribution of the on-axis laser electric field at
${E}_y$
) at different times. The orange curve is the electron density on-axis. (d) Spectral evolution as a function of the propagation time. (e) Spectral distribution of the on-axis laser electric field at
![]() $t=150{T}_0$
(blue),
$t=150{T}_0$
(blue),
![]() $2250{T}_0$
(black) and
$2250{T}_0$
(black) and
![]() $3600{T}_0$
(red). (f) Temporal profile of the mid-IR electric field at
$3600{T}_0$
(red). (f) Temporal profile of the mid-IR electric field at
![]() $t=3600{T}_0$
.
$t=3600{T}_0$
.
The compression of the NCLP enhances the generation efficiency of the mid-IR pulse and shortens the length of the plasma. Therefore, in order to investigate the pulse compression process in detail, we present the refractive index distribution of the drive laser. Figure 3 shows the refractive index and the evolution of pulse length of the NCLP. Meanwhile, the case without chirp is also given for comparison. Since both the
![]() ${v}_{\mathrm{p}}$
and
${v}_{\mathrm{p}}$
and
![]() ${v}_{\mathrm{g}}$
are a function of laser frequency, the NCLP has different distribution of refractive index
${v}_{\mathrm{g}}$
are a function of laser frequency, the NCLP has different distribution of refractive index
![]() $\eta$
, SPM and GVD for different frequency component. Figures 3(a) and 3(b) show the laser electric field and refractive index at
$\eta$
, SPM and GVD for different frequency component. Figures 3(a) and 3(b) show the laser electric field and refractive index at
![]() $t=150{T}_0$
for the cases of the chirp parameter
$t=150{T}_0$
for the cases of the chirp parameter
![]() $b=-0.07$
and un-chirped laser pulses, respectively, where the results marked by the red curve (
$b=-0.07$
and un-chirped laser pulses, respectively, where the results marked by the red curve (
![]() ${\eta}_{\mathrm{PIC}}$
) come from the PIC simulation, and those marked by the black curve (
${\eta}_{\mathrm{PIC}}$
) come from the PIC simulation, and those marked by the black curve (
![]() ${\eta}_{\mathrm{t}}$
) are the analytical results from Equation (4). For the NCLP, due to the change of frequency component, we have
${\eta}_{\mathrm{t}}$
) are the analytical results from Equation (4). For the NCLP, due to the change of frequency component, we have
![]() $\partial \eta /\partial \xi >0$
caused by the fall of the refractive index at the low-frequency part of the NCLP, where the fall edge is experiencing a photon acceleration. However, for the un-chirped pulse, the refractive index is close to that at the tail of pulse.
$\partial \eta /\partial \xi >0$
caused by the fall of the refractive index at the low-frequency part of the NCLP, where the fall edge is experiencing a photon acceleration. However, for the un-chirped pulse, the refractive index is close to that at the tail of pulse.

Figure 3 Comparison of refractive index and evolution of the NCLP and un-chirped pulse. Longitudinal distribution of the laser electric field and refractive index in the cases of (a)
![]() $b=-0.07$
and (b) an un-chirped laser. (c), (d) The corresponding locations of the rise edge and the fall edge, corresponding to the case with and without chirp, respectively. The insets of (c) and (d) show the evolution of the laser peak electric field
$b=-0.07$
and (b) an un-chirped laser. (c), (d) The corresponding locations of the rise edge and the fall edge, corresponding to the case with and without chirp, respectively. The insets of (c) and (d) show the evolution of the laser peak electric field
![]() ${E}_{\mathrm{p}}$
.
${E}_{\mathrm{p}}$
.
To record the distance between the reference points and the pulse center, the position change of the rise edge and the fall edge in the propagation process is shown in Figures 3(c) and 3(d). Due to the plasma etching in the wakefield, the rise edges of the NCLP and un-chirped pulse both compress toward the center of the pulse, as shown by the red dots in Figures 3(c) and 3(d). However, the fall edge of the NCLP also compresses toward the center due to the positive refractive index gradient (photon acceleration). Therefore, at the earlier stage of interaction, the longitudinal bunching effect of the NCLP results from the photon acceleration and plasma etching. This compression on both edges results in a dramatic increase in pulse intensity and the efficient generation of a mid-IR pulse. The insets of Figures 3(c) and 3(d) show the evolution of the peak laser electric field. One can see that the intensity of the NCLP is significantly enhanced, approaching its maximum value of about
![]() $1.8\times {10}^{13}\;\mathrm{V}\;{\mathrm{m}}^{-1}$
(
$1.8\times {10}^{13}\;\mathrm{V}\;{\mathrm{m}}^{-1}$
(
![]() $9.2\times {10}^{12}\;\mathrm{V}\;{\mathrm{m}}^{-1}$
for the case of the un-chirped laser) at
$9.2\times {10}^{12}\;\mathrm{V}\;{\mathrm{m}}^{-1}$
for the case of the un-chirped laser) at
![]() $t=2000{T}_0$
, which verifies the feasibility of the chirped pulse compression scheme in Figure 1. After that, the electric field intensity gradually decreases due to the generation of mid-IR frequency components and the defocusing effect of the drive laser.
$t=2000{T}_0$
, which verifies the feasibility of the chirped pulse compression scheme in Figure 1. After that, the electric field intensity gradually decreases due to the generation of mid-IR frequency components and the defocusing effect of the drive laser.
The generated mid-IR pulse by photon deceleration is a few-cycle pulse, and its CEP is very important for subsequent applications, since the CEP can directly affect the process of laser–matter interaction. Due to the difference between the phase velocity and the group velocity of waves of different frequency, there must be a phase slip between the drive NCLP
![]() ${\mathrm{CEP}}_0$
and the generated mid-IR pulse
${\mathrm{CEP}}_0$
and the generated mid-IR pulse
![]() ${\mathrm{CEP}}_{\mathrm{MIR}}$
. When the CEP is dephased by
${\mathrm{CEP}}_{\mathrm{MIR}}$
. When the CEP is dephased by
![]() $2\pi$
, the propagation length of pulse is
$2\pi$
, the propagation length of pulse is
![]() ${L}_{2\pi}\simeq \left({n}_{\mathrm{c}}/{n}_{\mathrm{e}}\right){\lambda}_0$
[
Reference Huijts, Andriyash, Rovige, Vernier and Faure
58
]. Therefore, the CEP shift of the NCLP can be expressed as follows:
${L}_{2\pi}\simeq \left({n}_{\mathrm{c}}/{n}_{\mathrm{e}}\right){\lambda}_0$
[
Reference Huijts, Andriyash, Rovige, Vernier and Faure
58
]. Therefore, the CEP shift of the NCLP can be expressed as follows:
 $$\begin{align} \begin{array}{l@{}l}{\Delta}_{\mathrm{CEP}}\,& ={\mathrm{CEP}}_0-{\mathrm{CEP}}_{\mathrm{MIR}}\\ {}& \approx 2\pi \times \left(\frac{n_{\mathrm{e}}l}{n_{\mathrm{c}}{\lambda}_0}-\lfloor\frac{n_{\mathrm{e}}l}{n_{\mathrm{c}}{\lambda}_0}\rfloor\right)\end{array},\end{align}$$
$$\begin{align} \begin{array}{l@{}l}{\Delta}_{\mathrm{CEP}}\,& ={\mathrm{CEP}}_0-{\mathrm{CEP}}_{\mathrm{MIR}}\\ {}& \approx 2\pi \times \left(\frac{n_{\mathrm{e}}l}{n_{\mathrm{c}}{\lambda}_0}-\lfloor\frac{n_{\mathrm{e}}l}{n_{\mathrm{c}}{\lambda}_0}\rfloor\right)\end{array},\end{align}$$
where
![]() $\lfloor \rfloor$
is the least integer function and
$\lfloor \rfloor$
is the least integer function and
![]() $l$
is the length of the mid-IR pulse generation time. The phase of the generated mid-IR pulse should be consistent with that of the drive laser at the mid-IR pulse generation time. Then, the mid-IR pulse slips rapidly backwards into the bubble, where there are almost no electrons, that is,
$l$
is the length of the mid-IR pulse generation time. The phase of the generated mid-IR pulse should be consistent with that of the drive laser at the mid-IR pulse generation time. Then, the mid-IR pulse slips rapidly backwards into the bubble, where there are almost no electrons, that is,
![]() ${\omega}_{\mathrm{p}}\approx 0$
,
${\omega}_{\mathrm{p}}\approx 0$
,
![]() ${v}_{\mathrm{p}}\approx {v}_{\mathrm{g}}\approx c$
. Therefore, the
${v}_{\mathrm{p}}\approx {v}_{\mathrm{g}}\approx c$
. Therefore, the
![]() ${\Delta}_{\mathrm{CEP}}$
between the drive laser and the mid-IR pulse is fixed at the generation time. To illustrate this point, the dependence of the
${\Delta}_{\mathrm{CEP}}$
between the drive laser and the mid-IR pulse is fixed at the generation time. To illustrate this point, the dependence of the
![]() ${\mathrm{CEP}}_{\mathrm{MIR}}$
at
${\mathrm{CEP}}_{\mathrm{MIR}}$
at
![]() $t=3600{T}_0$
on the
$t=3600{T}_0$
on the
![]() ${\mathrm{CEP}}_0$
is shown in Figure 4. One can see that the phase difference between
${\mathrm{CEP}}_0$
is shown in Figure 4. One can see that the phase difference between
![]() ${\mathrm{CEP}}_0$
and
${\mathrm{CEP}}_0$
and
![]() ${\mathrm{CEP}}_{\mathrm{MIR}}$
is fixed for the fixed plasma density and length, and there is a nearly linear relationship of the phase difference
${\mathrm{CEP}}_{\mathrm{MIR}}$
is fixed for the fixed plasma density and length, and there is a nearly linear relationship of the phase difference
![]() ${\Delta}_{\mathrm{CEP}}$
. The mid-IR pulse peak electric field changes with the variation of the initial
${\Delta}_{\mathrm{CEP}}$
. The mid-IR pulse peak electric field changes with the variation of the initial
![]() $\mathrm{{CEP}}_0$
, and the direction of peak electric field changes periodically, that is, a linear change from
$\mathrm{{CEP}}_0$
, and the direction of peak electric field changes periodically, that is, a linear change from
![]() $-\pi$
to
$-\pi$
to
![]() $0$
with
$0$
with
![]() ${\mathrm{CEP}}_0$
changing from
${\mathrm{CEP}}_0$
changing from
![]() $0$
to
$0$
to
![]() $\pi$
, as shown in Figure 4(a). The inset of Figure 4(a) provides the temporal variation of the mid-IR electric field with different
$\pi$
, as shown in Figure 4(a). The inset of Figure 4(a) provides the temporal variation of the mid-IR electric field with different
![]() ${\mathrm{CEP}}_0$
(
${\mathrm{CEP}}_0$
(
![]() $0$
,
$0$
,
![]() $\pi /2$
and
$\pi /2$
and
![]() $\pi$
). One can be seen from Figure 4(b) that the
$\pi$
). One can be seen from Figure 4(b) that the
![]() ${\mathrm{CEP}}_{\mathrm{MIR}}$
is locked on the
${\mathrm{CEP}}_{\mathrm{MIR}}$
is locked on the
![]() ${\mathrm{CEP}}_0$
, and the difference of
${\mathrm{CEP}}_0$
, and the difference of
![]() ${\mathrm{CEP}}_{\mathrm{MIR}}$
and
${\mathrm{CEP}}_{\mathrm{MIR}}$
and
![]() ${\mathrm{CEP}}_0$
is about 0.6
${\mathrm{CEP}}_0$
is about 0.6
![]() $\pi$
at
$\pi$
at
![]() $t=3600{T}_0$
, which is in excellent agreement with the theoretical calculation
$t=3600{T}_0$
, which is in excellent agreement with the theoretical calculation
![]() ${\Delta}_{\mathrm{CEP}}\approx 0.6\;\pi$
.
${\Delta}_{\mathrm{CEP}}\approx 0.6\;\pi$
.

Figure 4 The evolution of the CEP at
![]() $t=3600{T}_0$
. (a) The generated mid-IR electric field as a function of the initial drive pulse phase
$t=3600{T}_0$
. (a) The generated mid-IR electric field as a function of the initial drive pulse phase
![]() $\mathrm{CEP}_0$
. The inset shows the electric field waveform for different
$\mathrm{CEP}_0$
. The inset shows the electric field waveform for different
![]() $\mathrm{CEP}_0$
of the initial drive pulse (
$\mathrm{CEP}_0$
of the initial drive pulse (
![]() $0$
, blue dashed;
$0$
, blue dashed;
![]() $\pi /2$
, black solid;
$\pi /2$
, black solid;
![]() $\pi$
, red dot dash). (b) The phase evolution of the mid-IR electric field with
$\pi$
, red dot dash). (b) The phase evolution of the mid-IR electric field with
![]() $\mathrm{CEP}_0$
variation.
$\mathrm{CEP}_0$
variation.
4 Discussion
The process and efficiency of mid-IR pulse generation with the chirp parameter of
![]() $b=-0.07$
have been expatiated in the above section. It is significant that the NCLP can effectively enhance the energy conversion efficiency of mid-IR pulses when the NCLP is rapidly compressed in the plasma. To investigate the maximum energy conversion efficiency (
$b=-0.07$
have been expatiated in the above section. It is significant that the NCLP can effectively enhance the energy conversion efficiency of mid-IR pulses when the NCLP is rapidly compressed in the plasma. To investigate the maximum energy conversion efficiency (
![]() $\mathrm{Effi}_{\mathrm{max}}$
) with different chirp parameters, we make the NCLP incident into a semi-infinite plasma channel at
$\mathrm{Effi}_{\mathrm{max}}$
) with different chirp parameters, we make the NCLP incident into a semi-infinite plasma channel at
![]() $x\ge 0$
. We show the results of different negative chirp parameters in Table 1, where
$x\ge 0$
. We show the results of different negative chirp parameters in Table 1, where
![]() ${t}_{\mathrm{MIR}}$
is the diagnosing time. The rapid and drastic compression of the NCLP enhances the intensity of the drive pulse and the plasma perturbation, which make the generation time of the mid-IR pulses earlier. It can be seen in Table 1 that the energy conversion efficiency with
${t}_{\mathrm{MIR}}$
is the diagnosing time. The rapid and drastic compression of the NCLP enhances the intensity of the drive pulse and the plasma perturbation, which make the generation time of the mid-IR pulses earlier. It can be seen in Table 1 that the energy conversion efficiency with
![]() $b=-0.07$
is increased by about 2.6 times as compared to the case of the un-chirped pulse. The improvement of energy conversion efficiency can be attributed to the chirp variation with the same initial laser intensity. The NCLP with b = –0.07 corresponds to the Fourier limit duration of about 2.9 fs, which approaches the single laser period of the
$b=-0.07$
is increased by about 2.6 times as compared to the case of the un-chirped pulse. The improvement of energy conversion efficiency can be attributed to the chirp variation with the same initial laser intensity. The NCLP with b = –0.07 corresponds to the Fourier limit duration of about 2.9 fs, which approaches the single laser period of the
![]() $0.8\;\unicode{x3bc} \mathrm{m}$
wavelength. Therefore,
$0.8\;\unicode{x3bc} \mathrm{m}$
wavelength. Therefore,
![]() $b=-0.07$
or
$b=-0.07$
or
![]() $R\approx 18.9\;\mathrm{nm}/\mathrm{fs}$
is the optimum chirp parameter. In contrast, the energy conversion efficiency with
$R\approx 18.9\;\mathrm{nm}/\mathrm{fs}$
is the optimum chirp parameter. In contrast, the energy conversion efficiency with
![]() $b=0.07$
is only about
$b=0.07$
is only about
![]() $1\%$
with the peak intensity of
$1\%$
with the peak intensity of
![]() $6.3\times {10}^{16}\;\mathrm{W}\;{\mathrm{cm}}^{-2}$
, as shown in Figure S1 of the supplementary information. In addition, the generation of mid-IR pulses can be influenced by the plasma density and the down ramp length. More information about the robustness can be seen in the supplementary information.
$6.3\times {10}^{16}\;\mathrm{W}\;{\mathrm{cm}}^{-2}$
, as shown in Figure S1 of the supplementary information. In addition, the generation of mid-IR pulses can be influenced by the plasma density and the down ramp length. More information about the robustness can be seen in the supplementary information.
Table 1 The maximum energy conversion efficiency (
![]() ${\mathrm{Effi}}_{\mathrm{max}}$
) of the generated mid-IR pulse with different chirp parameters.
${\mathrm{Effi}}_{\mathrm{max}}$
) of the generated mid-IR pulse with different chirp parameters.

Finally, we carry out a full-scale 3D PIC simulation as well to ensure the reliability of our scheme. The box size is
![]() $60\;\unicode{x3bc} \mathrm{m}$
(x)
$60\;\unicode{x3bc} \mathrm{m}$
(x)
![]() $\times$
$\times$
![]() $60\;\unicode{x3bc} \mathrm{m}$
(y)
$60\;\unicode{x3bc} \mathrm{m}$
(y)
![]() $\times$
$\times$
![]() $60\;\unicode{x3bc} \mathrm{m}$
(z) with grid cells of 1500
$60\;\unicode{x3bc} \mathrm{m}$
(z) with grid cells of 1500
![]() $\times$
240
$\times$
240
![]() $\times$
240 and four macroparticles per cell. The incident laser with spot size of
$\times$
240 and four macroparticles per cell. The incident laser with spot size of
![]() $20\;\unicode{x3bc} \mathrm{m}$
is used in the 3D simulation. The plasma channel has a very long length of plateau, and it allows us to find the best position to generate mid-IR pulses. Transverse slice images of the electric field and electron density at
$20\;\unicode{x3bc} \mathrm{m}$
is used in the 3D simulation. The plasma channel has a very long length of plateau, and it allows us to find the best position to generate mid-IR pulses. Transverse slice images of the electric field and electron density at
![]() $t=50{T}_0$
,
$t=50{T}_0$
,
![]() $t=3000{T}_0$
and
$t=3000{T}_0$
and
![]() $t=5000{T}_0$
are shown in Figures 5(a)–5(c). One can see in Figures 5(a) and 5(b) that the drive laser pulse excites a stable bubble, which will be a container to accommodate the mid-IR pulse. The mid-IR pulses can be efficiently generated, and the bubble is full of mid-IR pulses, as shown in Figure 5(c). In addition, we can see that the self-injected electrons overlap spatially with the generated mid-IR pulse. Although the energy exchange can occur between the electron beam and the generated mid-IR pulse, the electron beam is not able to seriously affect the beam quality of the mid-IR pulse due to the short interaction time in our scheme. The spectra at different times are shown in Figure 5(d), where one can see that the maximum central wavelength of the mid-IR pulse is
$t=5000{T}_0$
are shown in Figures 5(a)–5(c). One can see in Figures 5(a) and 5(b) that the drive laser pulse excites a stable bubble, which will be a container to accommodate the mid-IR pulse. The mid-IR pulses can be efficiently generated, and the bubble is full of mid-IR pulses, as shown in Figure 5(c). In addition, we can see that the self-injected electrons overlap spatially with the generated mid-IR pulse. Although the energy exchange can occur between the electron beam and the generated mid-IR pulse, the electron beam is not able to seriously affect the beam quality of the mid-IR pulse due to the short interaction time in our scheme. The spectra at different times are shown in Figure 5(d), where one can see that the maximum central wavelength of the mid-IR pulse is
![]() $6\;\unicode{x3bc} \mathrm{m}$
at
$6\;\unicode{x3bc} \mathrm{m}$
at
![]() $t=5000{T}_0$
. The average refractive index gradient is estimated to be
$t=5000{T}_0$
. The average refractive index gradient is estimated to be
![]() $-9.3\times {10}^{-3}\;{\unicode{x3bc} \mathrm{m}}^{-1}$
at the conversion stage from
$-9.3\times {10}^{-3}\;{\unicode{x3bc} \mathrm{m}}^{-1}$
at the conversion stage from
![]() $t=4000{T}_0$
to
$t=4000{T}_0$
to
![]() $t\,{=}\,5000{T}_0$
in the 3D PIC simulation. According to Equation (5), the average refractive index gradient of
$t\,{=}\,5000{T}_0$
in the 3D PIC simulation. According to Equation (5), the average refractive index gradient of
![]() $-9.3\times {10}^{-3}\;{\unicode{x3bc} \mathrm{m}}^{-1}$
will generate the mid-IR pulse wavelength of
$-9.3\times {10}^{-3}\;{\unicode{x3bc} \mathrm{m}}^{-1}$
will generate the mid-IR pulse wavelength of
![]() $6.7\;\unicode{x3bc} \mathrm{m}$
in a
$6.7\;\unicode{x3bc} \mathrm{m}$
in a
![]() $800\;\unicode{x3bc} \mathrm{m}$
convertor. The inset of Figure 5(d) shows the temporal profile of the on-axis mid-IR electric field with the FWHM duration of 80 fs. The simulation result shows that one can obtain a mid-IR pulse with the central wavelength of
$800\;\unicode{x3bc} \mathrm{m}$
convertor. The inset of Figure 5(d) shows the temporal profile of the on-axis mid-IR electric field with the FWHM duration of 80 fs. The simulation result shows that one can obtain a mid-IR pulse with the central wavelength of
![]() $6\;\unicode{x3bc} \mathrm{m}$
and the normalized peak intensity of
$6\;\unicode{x3bc} \mathrm{m}$
and the normalized peak intensity of
![]() ${a}_{\mathrm{MIR}}\approx 3.5$
at
${a}_{\mathrm{MIR}}\approx 3.5$
at
![]() $t\,{=}\,5000{T}_0$
. Further, the maximum energy conversion efficiency can reach 6.3% with the spectral width of 4.3–
$t\,{=}\,5000{T}_0$
. Further, the maximum energy conversion efficiency can reach 6.3% with the spectral width of 4.3–
![]() $20\;\unicode{x3bc} \mathrm{m}$
at
$20\;\unicode{x3bc} \mathrm{m}$
at
![]() $t=5300{T}_0$
. More 3D simulation and comparison details for the un-chirped case can be found in the supplementary information.
$t=5300{T}_0$
. More 3D simulation and comparison details for the un-chirped case can be found in the supplementary information.

Figure 5 3D simulation of mid-IR generation with the NCLP. (a)–(c) The distributions of the plasma density (
![]() ${n}_{\mathrm{e}}$
) and the transverse electric field (
${n}_{\mathrm{e}}$
) and the transverse electric field (
![]() ${E}_y$
) at different times obtained from 3D PIC simulation. (d) Spectral distribution of the on-axis laser electric field at
${E}_y$
) at different times obtained from 3D PIC simulation. (d) Spectral distribution of the on-axis laser electric field at
![]() $t=50{T}_0$
(blue) and
$t=50{T}_0$
(blue) and
![]() $5000{T}_0$
(red). The inset is the temporal profile of the mid-IR electric field at
$5000{T}_0$
(red). The inset is the temporal profile of the mid-IR electric field at
![]() $t=5000{T}_0$
.
$t=5000{T}_0$
.
5 Conclusion
In conclusion, we have proposed and numerically demonstrated a scheme to effectively improve the generation efficiency of high-intensity, few-cycle and long carrier wavelength mid-IR pulses by controlling the chirp parameters of the NCLP. Compared with the case of the un-chirped pulse, due to the difference of phase velocity and group velocity of different frequency components of the NCLP, the plasma etching and the special refractive index can make the pulse rapidly compress longitudinally, and this compression can effectively enhance the pulse intensity and plasma density perturbation. As a result, the mid-IR pulses can be produced faster and the energy conversion efficiency becomes higher. The 2D PIC simulation results show that a relativistic few-cycle mid-IR pulse with a center wavelength of
![]() $7.9\;\unicode{x3bc} \mathrm{m}$
can be generated at an interaction time of
$7.9\;\unicode{x3bc} \mathrm{m}$
can be generated at an interaction time of
![]() $3600{T}_0$
with the chirped parameter of
$3600{T}_0$
with the chirped parameter of
![]() $b=-0.07$
. Meanwhile, the negatively chirped pulse can significantly improve the energy conversion efficiency of mid-IR pulses. The maximum energy conversion efficiency is enhanced to about 5.0% in the case of
$b=-0.07$
. Meanwhile, the negatively chirped pulse can significantly improve the energy conversion efficiency of mid-IR pulses. The maximum energy conversion efficiency is enhanced to about 5.0% in the case of
![]() $b=-0.07$
at an interaction time of
$b=-0.07$
at an interaction time of
![]() $4125{T}_0$
. The 3D PIC simulation results also verify that our scheme can generate a relativistic mid-IR pulse with a higher energy conversion efficiency. The CEP of the generated mid-IR is also phase-locked with the central phase of the initial NCLP. Such efficient mid-IR sources may find many potential applications in high-field physics and ultrafast science, for example, THz emission and charged particle acceleration.
$4125{T}_0$
. The 3D PIC simulation results also verify that our scheme can generate a relativistic mid-IR pulse with a higher energy conversion efficiency. The CEP of the generated mid-IR is also phase-locked with the central phase of the initial NCLP. Such efficient mid-IR sources may find many potential applications in high-field physics and ultrafast science, for example, THz emission and charged particle acceleration.
Acknowledgements
We acknowledge the Tianhe supercomputer team for computing resources. This work was supported by the National Key Research and Development Program of China (No. 2018YFA0404802), the National Natural Science Foundation of China (Nos. 12005297, 11875319, 12135009, and 12275356), the Science and Technology Innovation Program of Hunan Province (No. 2020RC4020), the Research Project of NUDT (No. ZK21-12) and the Hunan Provincial Research and Innovation Foundation for Graduate Students (Nos. CX20200002, CX20200038, and CX20210062).
Supplementary Materials
To view supplementary material for this article, please visit http://doi.org/10.1017/hpl.2023.51.