3.1 Time-resolved investigations of carrier dynamics in fused silica glass

The nature and the morphological aspect of optical damage, namely the potential onset of refractive index changes, regular voids or catastrophic runaway is strongly dependent on the deposited energy. The low exposure domain, at pump energies below or close to observable modifications, was regularly investigated and indicates fast relaxation (100 fs) and trapping of free carriers on excitonic states self-trapped due to the electronic polarization of the matrix. These evolve to Frenkel pairs and the Si–O bond scission leads to nonbridging oxygen hole center (NBOHC) and $E^{\prime }$ centers accompanying a soft isotropic increase of the refractive index upon pulse accumulation. It was argued before^{[Reference Velpula, Bhuyan, Courvoisier, Zhang, Colombier and Stoian7, Reference Mishchik, D’Amico, Velpula, Mauclair, Ouerdane, Boukenter and Stoian22]} that, most probably, the weak positive index changes regime results from defect-induced matrix densification without visible thermal assistance in driving the structural metastability. Photoinscription in this range leads to type I index changes and low-loss waveguides^{[Reference Osellame, Cerullo and Ramponi1]}. Increasing the incoming laser pulse energy above the critical power for self-focusing (corresponding to sub- $\unicode[STIX]{x03BC}\text{J}$ ranges), the morphology of the excited region changes to a modulated positive and negative index region. A detailed description of the nonlinear propagation factors leading to this geometry was given in Ref. [Reference Burakov, Bulgakova, Stoian, Mermillod-Blondin, Audouard, Rosenfeld, Husakou and Hertel23]. The onset of the formation of void-like low index regions can be assigned to self-focusing and expansion, while the follow-up positive index trail indicates filamentation characteristics^{[Reference Burakov, Bulgakova, Stoian, Mermillod-Blondin, Audouard, Rosenfeld, Husakou and Hertel23, Reference Mermillod-Blondin, Bonse, Rosenfeld, Hertel, Meshcheryakov, Bulgakova, Audouard and Stoian24]}. Both regions are permanently visible after single-shot interaction. If low-density regions can originate from thermomechanical expansion, the void formation is usually assigned to a microexplosion phenomenon^{[Reference Gamaly, Juodkazis, Nishimura, Misawa, Luther-Davies, Hallo, Nicolai and Tikhonchuk25]} being driven by high pressure, high temperature material states against the mechanical resistance of the surrounding cold material. Beyond this, at high input energies, a catastrophic, stochastic-like damage occurs comprising multiple voids and index regions of different contrasts. This signals strongly unstable propagation with multiple points of energy concentration where thermodynamic conditions for void expansion and stress development are achieved. We concentrate here on energetic conditions in the catastrophic regime as it allows to study the relaxation behavior in strong excitation conditions at the focus and in low excitation conditions at the neighboring regions in the spatial distribution of the incoming Gaussian pulse.

Figure 1. Time-resolved observation of laser excitation and subsequent relaxation in fused silica in (a) OTM and (b) PCM modes at energies significantly above the void-formation threshold (high-energy range). Input energy $E=43~\unicode[STIX]{x03BC}\text{J}$ and pulse duration $t_{p}=160$  fs. Two characteristic regions in terms of dynamics are indicated as LF region and HF region. (c) Estimated maximum electronic density at zero delay, at the excitation peak. (d) PCM aspect of the permanent damage. Transmission and relative phase change scale bars are given, as well as normalized (to critical density at 800 nm) scales for carrier density. The laser pulse is coming from the left.

The first set of high-energy time and space-resolved excitation snapshots in a- $\text{SiO}_{2}$ are given in Figure 1 in terms of transient OTM images [Figure 1(a)], PCM images [Figure 1(b,d)] and Drude-based carrier densities [Figure 1(c)]. The input energy of $E=43~\unicode[STIX]{x03BC}\text{J}$ is well-above the threshold for the void formation (around $0.23~\unicode[STIX]{x03BC}\text{J}$ ). The transmission signatures are determinantly originating in the development of free carriers and reflect mainly the properties of a collisional electron–hole plasma but they may equally involve mobile excitonic states bordering the allowed energy bands. With reference to the OTM micrographs, characteristic to this figure is the existence of two spatially distinct regions with two characteristic dynamics. The low fluence (LF) region located before the pulse concentration at the focus [Figure 1(a)] is subject to low-energy concentration while a high fluence (HE) region is located along the confocal domain and corresponds to the maximal energy concentration (corresponding to fluences above $1000~\text{J}/\text{cm}^{2}$ in vacuum). Given the light defocusing strength of self-induced carriers, the local fluences in the bulk are significantly lower. They preserve nevertheless considerable values, above the material destruction point. The multiple points before the focus are an effect of diffraction at the objective aperture and scattering of wavefronts toward the propagation axis^{[Reference Mauclair, Mermillod-Blondin, Landon, Huot, Rosenfeld, Hertel, Audouard, Myiamoto and Stoian26]}.

The LF region [Figure 1(a)] shows a fast evolution of OTM with a rapid recovery. This corresponds to a fast electronic decay with a sub-ps decay constant. This rapid characteristic dynamics is the signature of a carrier trapping mechanism where free carriers are trapped into immobile excitonic states^{[Reference Audebert, Daguzan, Dos Santos, Gauthier, Guizard, Hamoniaux, Krastev, Martin, Petite and Antonetti6]} associated with localized structural changes. Evidence of NBOHC was found in this regime^{[Reference Velpula, Bhuyan, Courvoisier, Zhang, Colombier and Stoian7, Reference Mishchik, D’Amico, Velpula, Mauclair, Ouerdane, Boukenter and Stoian22, Reference Grojo, Gertsvolf, Lei, Barillot, Rayner and Corkum27]} with signs of structural compaction. This is equally a typical material modification regime in terms of photon doses for the photoinscription of soft, low contrast refractive index changes, also obtained in intensity clamping conditions. Complementary PCM shows the variation of the optical phase deriving from a mix of electronic and structural effects. We suggest that the latter are preponderant in view of the rapid electronic decay. The comparative observation of PCM images [Figure 1(b)] with their representation of the acquired optical phase shows that associated structural modifications start almost simultaneously with electronic excitation, suggesting a rapid response to electronic excitation. The dark regions correspond to a fast (and transient) index increase (the residual white may be an artefact of PCM at high index contrast). However, this structural perturbation initiated by electronic excitation within the LF region has a significantly longer lifetime than the carrier plasma and survives up to ns ranges. This transient phase shift can then be put in relation to the characteristic structural and electronic local rearrangement related to STE evolution (displacement of oxygen atoms and the onset of excitonic localized bands in the forbidden gap)^{[Reference Audebert, Daguzan, Dos Santos, Gauthier, Guizard, Hamoniaux, Krastev, Martin, Petite and Antonetti6, Reference Velpula, Bhuyan, Courvoisier, Zhang, Colombier and Stoian7]}. Si–O molecular bonding is loosening and a more compacted structural arrangement (lower size rings) can be obtained in the fused silica matrix. Due to its fast onset, the phase dynamics seems less related to local heating but heat contributions cannot be excluded. The typical level of excitation in this range is a fraction of the critical density at 800 nm [Figure 1(c)]. It is though to be noted that for a glass with a positive thermo-optic coefficient, a fast increase of temperature would equally lead to a positive index change.

The OTM dynamics in the HF region is different, as the increase of the incoming fluence delivers a radically distinct behavior in terms of relaxation times [Figure 1(a)]. As opposed to what is typically seen for the low dose regime, we note now a persistent long-living high level of absorption (tens of percent) and consequently, a relatively long relaxation time for the axial region (on hundreds of ps, up to the ns). The long-living absorption trail is no longer consistent with fast trapping mechanisms via deformation potentials, suggesting a matrix structural state unable to trap carriers. This may be indicative of strongly destabilized molecular bonds or of a rapid onset of a low viscosity state with vibrational activity. The corresponding PCM observations seem to confirm the existing and long-living electron plasma on longer timescales, although the interpretation is more difficult due to the mixed amplitude and phase properties of the object and the plasma radiative emission. An estimation of the carrier density at the peak of the laser pulse leads to values close to the critical density at 800 nm. It is though to be noted that, in view of the collisional properties of the plasma (sub-fs collision times) which give a strongly dissipative character, no sharp resonance is to be expected at the critical density, and therefore the use of a critical density is just indicative but without the relevance of a sudden absorptive regime. Carrier densities in this range are sufficient to rise the matrix temperature after relaxation at considerable temperature values.

The permanent damage morphology visible in Figure 1(d) consists of a more or less random succession of void-like and high index zones only in the confocal domain in the high excitation range, the changes in the perifocal range being too weak to be observed in a single-shot event. It is therefore expectable that this characteristic morphology modification involves transitions via lower viscosity states (even though perhaps not yet a fully developed liquid phase) and the onset of the void is a result of the mechanically induced rarefaction^{[Reference Mermillod-Blondin, Bonse, Rosenfeld, Hertel, Meshcheryakov, Bulgakova, Audouard and Stoian24, Reference Gamaly, Juodkazis, Nishimura, Misawa, Luther-Davies, Hallo, Nicolai and Tikhonchuk25]}. Photoluminescence signatures indicated the presence of oxygen deficiency centers (ODC) in the vicinity of the void interfaces and the onset of molecular oxygen^{[Reference Mishchik, D’Amico, Velpula, Mauclair, Ouerdane, Boukenter and Stoian22]}. These support present scenarios of molecular decomposition that assume that enough energy is provided to the glass matrix to facilitate the onset of gas-phase transformation in void-like domains^{[Reference Lancry, Poumellec, Canning, Cook, Poulin and Brisset20, Reference Bressel, de Ligny, Gamaly, Rode and Juodkazis28]}. The absence of strong NBOHC yield in the regions of the catastrophic damage^{[Reference Mishchik, D’Amico, Velpula, Mauclair, Ouerdane, Boukenter and Stoian22]} corroborated with the long dynamics of the relaxation times seems to confirm a significant decrease of the electron trapping strength, as matrix heating or vibrational activity associated to lower viscosity kicks in and lowers the molecular polarization potential. Alternative pathways of structural reorganization of the matrix in the presence of significant bond-breaking, favored by excessive heat and pressure, may contribute to the absence of NBOHC. A sketch of defect redistribution in the high-energy damage area^{[Reference Mishchik, D’Amico, Velpula, Mauclair, Ouerdane, Boukenter and Stoian22, Reference Stoian, Mishchik, Cheng, Mauclair, D’Amico, Colombier and Zamfirescu29]} is given in Figure 2. The photoluminescence spectrum is taken under conditions of excitation at 325 nm, resonant with NBOHC states. This observation shows that the rapid relaxation domain at low doses is the preferential region for forming NBOHCs, a natural product of electron trapping and STE relaxation, while the axial damage shows molecular decomposition and sever bond-breaking regime with ODC formation. Similar defect signatures appear equally in neighboring zones subjected to thermomechanical transformation but less to light exposure. This suggests a competition of electronic and mechanical bond-breaking effects above plastic yielding.

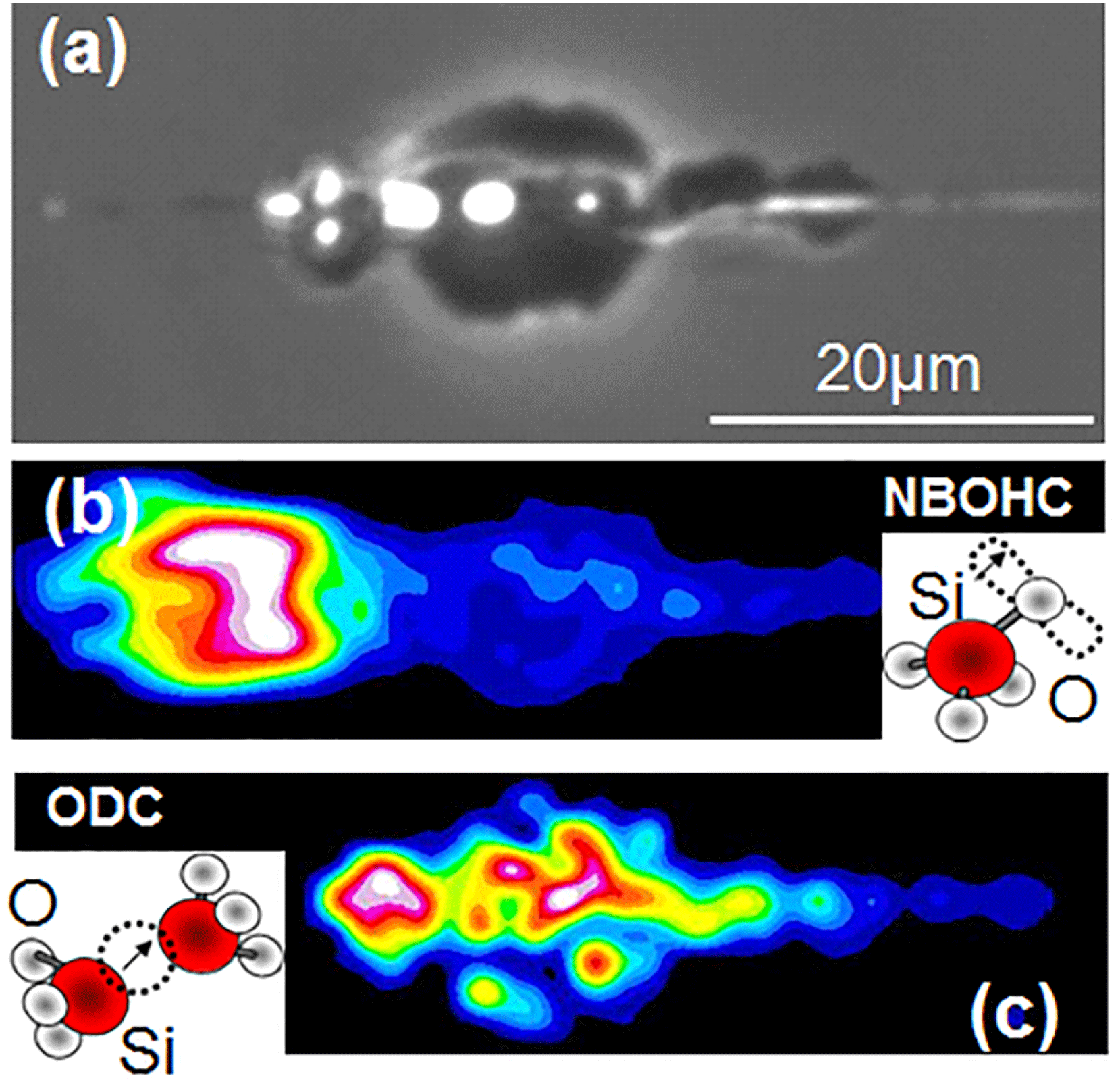
Figure 2. Post-irradiation PCM and photoluminescence spectroscopy analysis in the fast and slow decay zones for a typical trace in the high-energy interaction domain^{[Reference Stoian, Mishchik, Cheng, Mauclair, D’Amico, Colombier and Zamfirescu29]}. (a) PCM of the modification region with the appearance of voids in the long-living excitation zone. (b) Generation of NBOHC in the soft, fast decay region, visualized by spatially mapping photoluminescence centered at 650 nm. (c) Accumulation of ODC in permanent void-like damage regions, with photoluminescence bands centered at 545 nm. A 325 nm excitation source is used.

To resume, we have observed in fused silica two characteristic fast and slow electron dynamics ranges characterized by rather low or high carrier densities that translate into specific damage aspects culminating with catastrophic runway and stochastic void formation. This shows the pertinence of considering high- and low-energy density deposition domains, as paths of structural relaxation will be different.

3.2 Time-resolved investigations of carrier dynamics in borosilicate BK7 glass

Since fused silica is a glass with an atypical thermodynamic behavior (various anomalies in glass transition and in the thermomechanical evolution) and relatively low thermal expansion, it is interesting to perform a similar experiment of a different class of silicate glasses with a more common behavior [with results given in Figure 3]. We have chosen a borosilicate crown glass, the Schott BK7, a glass relying on silica and boric oxide as glass formers and light metallic impurities, but showing normal glass transition behavior. This implies that, upon cooling to the glassy state, the material density increases with the cooling time. Moreover, BK7 shows an approximately ten times higher thermal expansion coefficient facilitating expansion upon heating in the glassy state.

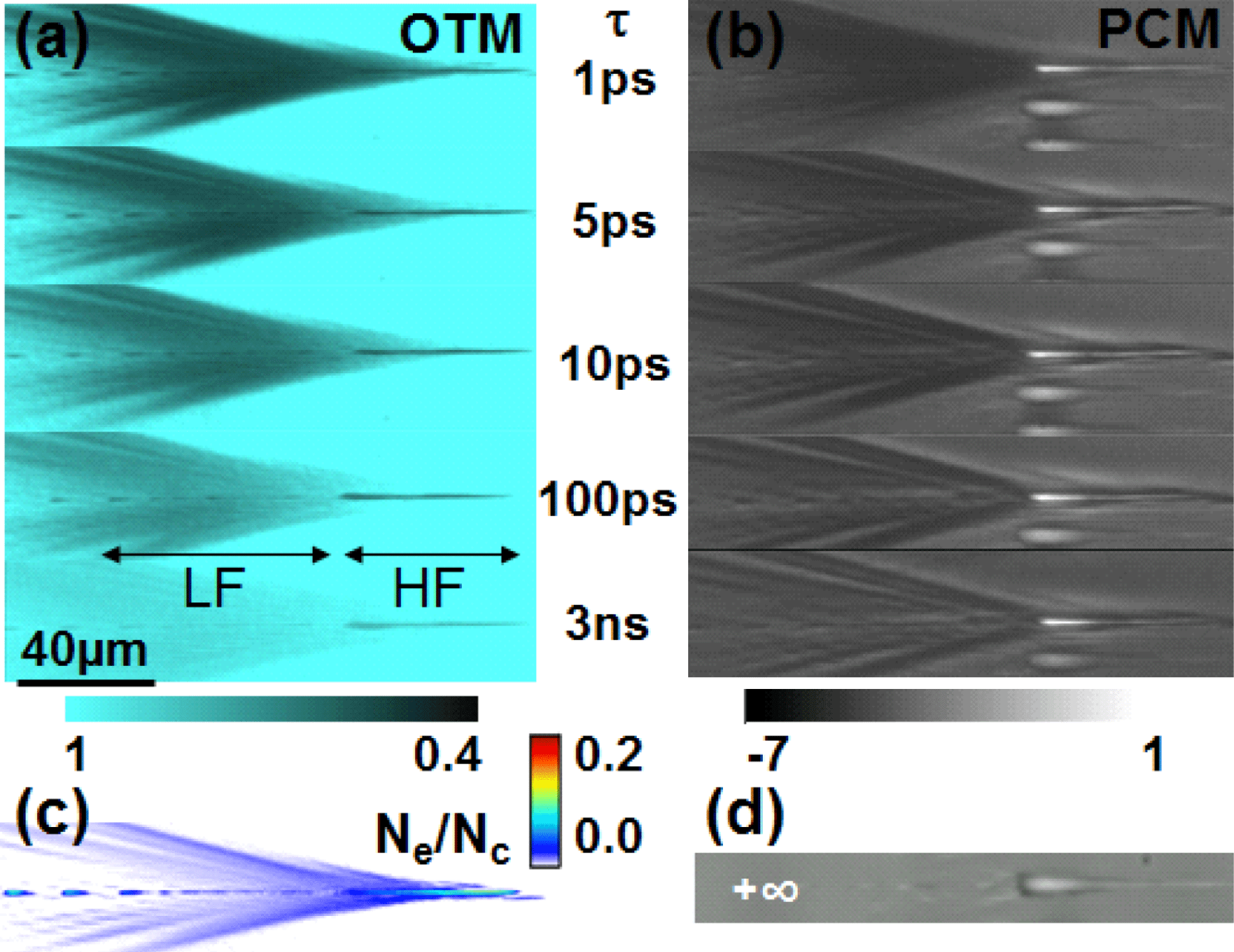
Figure 3. Time-resolved observation of excitation and relaxation in borosilicate BK7 in (a) OTM and (b) PCM modes at energies significantly above the void-formation threshold (high-energy range). Input energy $E=43~\unicode[STIX]{x03BC}\text{J}$ and pulse duration $t_{p}=160$  fs. Two characteristic regions in terms of dynamics are indicated as LF region and HF region. (c) Estimated peak electronic density at zero delay. (d) PCM aspect of the permanent damage. Transmission and relative phase change scale bars are given, as well as normalized (to critical density at 800 nm) scales for carrier density. The laser pulse is coming from the left.

Figures 3(a) and 3(b) shows the electronic relaxation and the corresponding optical response for high-energy excitation of BK7 ( $43~\unicode[STIX]{x03BC}\text{J}$ ). As in the case of fused silica, two regions can be discerned. In the LF region, the electronic density decays gradually with a characteristic time that exceeds 10 ps. Slightly shorter times (8 ps) were obtained at lower dose^{[Reference Mermillod-Blondin30]}, still significantly higher than what is expected for a- $\text{SiO}_{2}$ . The PCM optical shift shows that a transient structural destabilization follows the electronic excitation and survives the electronic decay to longer times. In the HF region, the decay time seems even longer, and the electronic contribution appears visible in both OTM and PCM. The peak electronic density [Figure 3(c)] that triggered this behavior is in the same order of magnitude, though somehow smaller, as for fused silica, despite a narrower band gap and an apriori higher excitation efficiency. This is intrinsically related to a certain light-scattering role of the free carriers, resisting thus to energy deposition.

In the energy range involved here, the permanent result of laser irradiation in BK7 in terms of damage appearance is a large, elongated, quasi-uniform region of negative refractive index change surrounded by a shallow layer of compressed material and low index features before the confocal region. Thus a rarefaction type of response is observed at the level of the glass matrix. It is conceivable that this corresponds to a local thermal expansion phenomenon leaving behind a low-density region^{[Reference Mermillod-Blondin, Burakov, Meshcheryakov, Bulgakova, Audouard, Rosenfeld, Husakou, Hertel and Stoian18]}.

We note that the observed dynamics for fused silica and borosilicate BK7 are quite general, irrespective of the input energy in the domain where catastrophic damage is achieved. The whole spatially and temporally resolved dynamics for a moderate energy is given in Figure 4 as OTM and PCM results, illustrating the existence of two characteristic dynamic behaviors for low and respectively high levels of excitation. Similar electronic and structural observations from OTM and PCM can be drawn, with fast carrier decay in LF-like regions (sub-ps for fused silica and few ps for BK7), but persisting structural signatures, and slow decay of carriers in HF-like domains. Thus the different relaxation dynamics suggests either soft or severe, thermally mediated structural changes. The difference in the relaxation speed for a- $\text{SiO}_{2}$ (sub-ps) and BK7 (ps) in the fast dynamics range (LF) suggest nevertheless a qualitative difference in the carrier decay mechanisms, with probable deviations in the trapping dynamics due to the compositional and band structure changes. For the HF, the apparent longer decay for fused silica in this range is related to the specific thermodynamic trajectory assisting the transition to lower viscosity, while a thermomechanical scenario seems more probable for BK7 in view of its mechanical properties.

Figure 4. Time-resolved observation of excitation and relaxation in borosilicate BK7 and fused silica in (a) OTM and (b) PCM modes at energies moderately above the void-formation threshold. Input energy $E=4~\unicode[STIX]{x03BC}\text{J}$ and pulse duration $t_{p}=160$  fs. Two characteristic regions in terms of dynamics are visible with fast and slow carrier decay times, and specific structural arrangements accompanying the two dynamics. The differentiation in fast and slow decay times is particularly observable for a- $\text{SiO}_{2}$ , with a less pregnant distinction in the case of BK7.

3.3 Mechanical relaxation

Even if the electronic concentration is quasi-sub-critical, in the catastrophic damage range the deposited energy can bypass the glass softening point. The long decay times suggest the achievement of low viscosity regions. In this range mechanical relaxation is expected via the release of pressure waves that reflect the geometry of the source^{[Reference Sakakura, Terazima, Shimotsuma, Miura and Hirao19, Reference Salleo, Génin, Feit, Rubenchik, Sands, Mao and Russo31]} and the pressure–temperature conditions in the excitation region. Shock relaxation, plastic yielding and elastic response can occur, reflecting the development of a hot, pressurized region^{[Reference Gamaly, Juodkazis, Nishimura, Misawa, Luther-Davies, Hallo, Nicolai and Tikhonchuk25]}. The observations here do not allow observing the initial shell-like shock which is confined on sub-micrometer scales, but merely the elastic propagation. The PCM observations for a- $\text{SiO}_{2}$ and BK7 at relatively long delays (2.5 ns, respectively 2.9 ns) given in Figures 5(a) and 5(b) show the emergence of pressure traveling waves with a velocity of $6.3~\text{km}/\text{s}$ (for fused silica), close to the longitudinal speed of sound. The overall form in case of a- $\text{SiO}_{2}$ [Figure 5(a)] comprises spherical and cylindrical components related to the void-like confined and filament-like elongated regions in the permanent damage morphology [Figure 1(d)]. The BK7 case [Figure 5(b)] shows a more planar geometry reflecting the extended void-like damage in Figure 3(d). At longer delay times [Figure 5(c)] in the case of fused silica, a second pressure wave appears with a delay of 2.7 ns. If it appears to suggest mechanical rupture or fracture, the origin of these second waves remains unknown. A similar phenomenon was recently observed in soda-lime glass^{[Reference Hendricks, Matylitsky, Domke and Huber32]}.

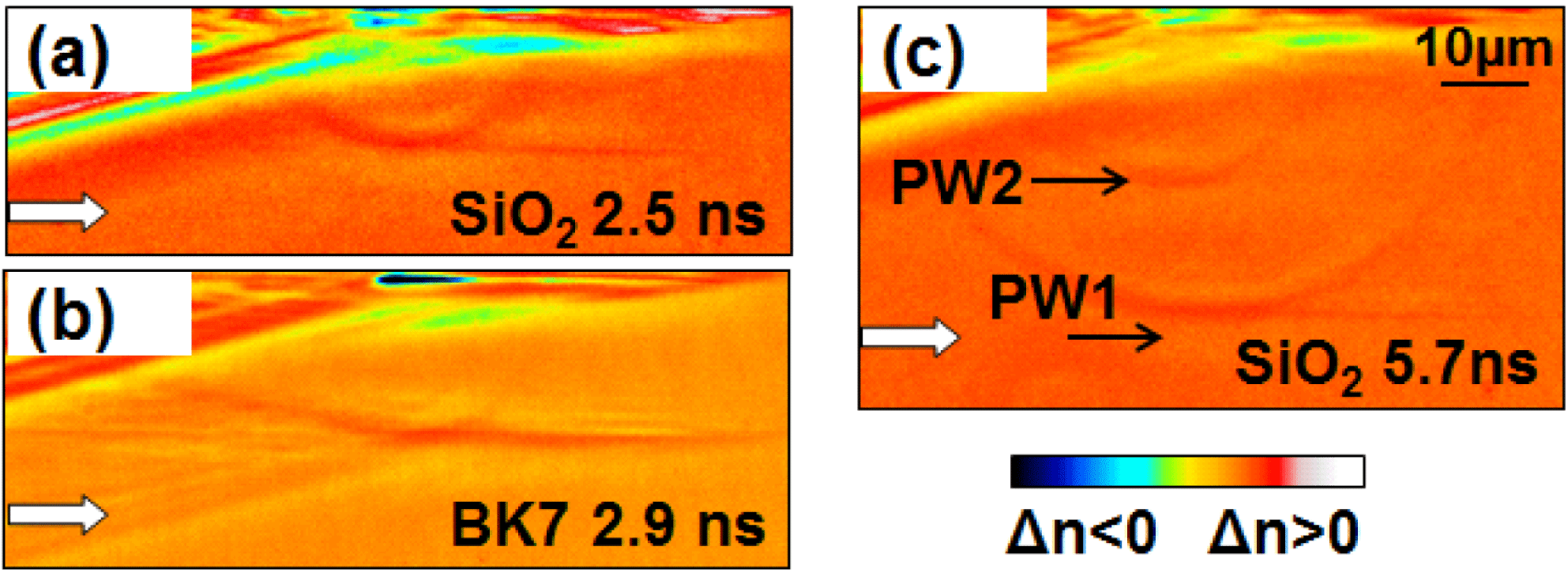
Figure 5. Long delay time (ns range) PCM observation of relaxation in (a) a- $\text{SiO}_{2}$ and (b) BK7 at energies significantly above the void-formation threshold (high-energy range). Input energy $E=43~\unicode[STIX]{x03BC}\text{J}$ and pulse duration $t_{p}=160$  fs. The color bar relates to evolving relative positive and negative refractive index changes. Pressure waves traveling at the speed of sound are to be observed as moving index change regions. (c) Longer delay time (5.7 ns) PCM observations in a- $\text{SiO}_{2}$ showing a second pressure wave forming with a delay of 2.7 ns. The laser pulse is coming from the left and the source is located at the top of each image.

The thermomechanical scenario is valid for a range of energies above the void-formation threshold inside the material and for a range of pulse durations. We follow below an example (illustrated in Figure 6) for observing the pressure waves initiated from the impact point in fused silica. The experimental detection concerns a moderate energy input of $4~\unicode[STIX]{x03BC}\text{J}$ for an incident laser pulse of 2 ps duration and time-resolved phase-contrast imaging. Figure 6(a) describes experimentally the dynamics of the acoustic waves generated after the deposition of the laser pulse energy. The PCM observations concern several delay times in the ns domain and show the formation and evolution of spherical and cylindrical components of the pressure waves (circular and linear geometries in the 2D figure section). For simulation, the spatial energy deposition pattern for an 150 fs laser pulse is calculated using a nonlinear light propagation code^{[Reference Burakov, Bulgakova, Stoian, Mermillod-Blondin, Audouard, Rosenfeld, Husakou and Hertel23]} serving then as input for the calculus of acoustic wave fields^{[Reference Treeby and Cox33]} emerging from the hot source. The simulated dynamics of the acoustic propagation is given in Figure 6(b). Note that the laser-induced formation of permanent material damage and density redistribution is not included in the present photo-acoustic simulations, but elements of densification/rarefaction were previously discussed^{[Reference Bulgakova34]}. The spherical and plane components, the compression and unload waves as well as the asymmetrical character are well reproduced. In the first ns after the interaction, the geometry of the compression wave conserves the aspect of the heat source. Spherical waves are initiated at the two extremities of the focal trace and cylindrical waves are launched perpendicular to the elongated source. The asymmetry is given by a stronger localization of the energy before the focus due to self-focusing. An unload component develops, reflecting also the initial mapping of energy deposition.

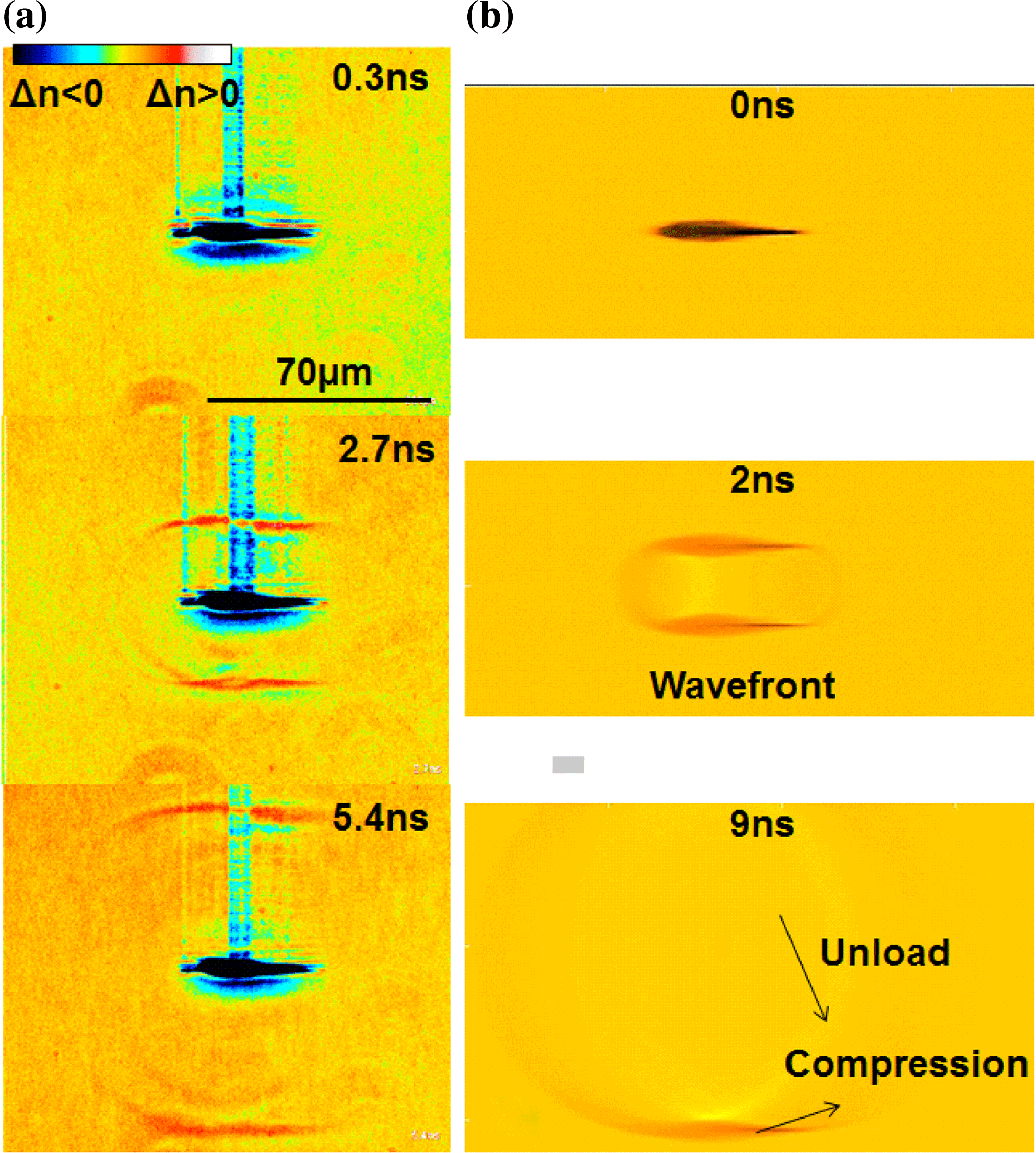
Figure 6. Photo-acoustic dynamics in fused silica observable at different time delays (a) in experimental time-resolved PCM images of evolving pressure waves and (b) in photo-acoustic simulation for a moderate energy input of $4~\unicode[STIX]{x03BC}\text{J}$ . Pulse duration is 2 ps for (a) and 150 fs for (b). The laser pulse is coming from the left. The color bar relates to evolving relative positive and negative refractive index changes.

3.4 Irradiation and control by temporally shaped pulses

The resulting modification at the level of the structure depends strongly on the ability to store energy into the glass matrix. Energy-dependent studies in the femtosecond range indicate that the local excitation does not vary significantly with the input intensity^{[Reference Burakov, Bulgakova, Stoian, Mermillod-Blondin, Audouard, Rosenfeld, Husakou and Hertel23]}, at least up to the point of uncontrollable, catastrophic damage. This is a direct consequence, at least for moderate focusing conditions, of the balance between pulse focusing strength including self-focusing and carrier defocusing, leading to a leveling of excitation similar to an intensity clamping effect. This leveling can be prevented by acting on the timing of the plasma formation^{[Reference Velpula, Bhuyan, Courvoisier, Zhang, Colombier and Stoian7]} and on its radial distribution, notably using the pulse envelope and spectral dispersion as an adjustable parameter. The consequence is that by elongating pulse envelopes, to a certain extent counterintuitively, the amount of excitation increases, despite a reduction into multiphoton ionization cross-section. Figure 7 resumes this situation for an input energy of $4~\unicode[STIX]{x03BC}\text{J}$ in fused silica, where the increase of pulse duration leads to a higher amount of energy concentration. This is first visible in the augmentation of the absorption level due to free carriers [Figure 7(a)], as well as in the subsequent increase in the magnitude of the launched pressure wave [Figure 7(b)]. A scenario discussing the role of pulse duration in defining the level and the shape of the absorption region was discussed earlier^{[Reference Velpula, Bhuyan, Courvoisier, Zhang, Colombier and Stoian7, Reference Burakov, Bulgakova, Stoian, Mermillod-Blondin, Audouard, Rosenfeld, Husakou and Hertel23]}. The pulse durations that achieved the maximal carrier density and pressure yield respectively are slightly shifted, indicating that the released pressure only partially reflects the initial energy concentration, part of the energy being spent in plastic compaction around the damage region. Nevertheless, this shows that concepts of optimal interaction can be defined with respect to the energy deposition. We note that a similar behavior was observed for double pulse sequences with separation times comparable to the elongation of the long pulse (not shown).

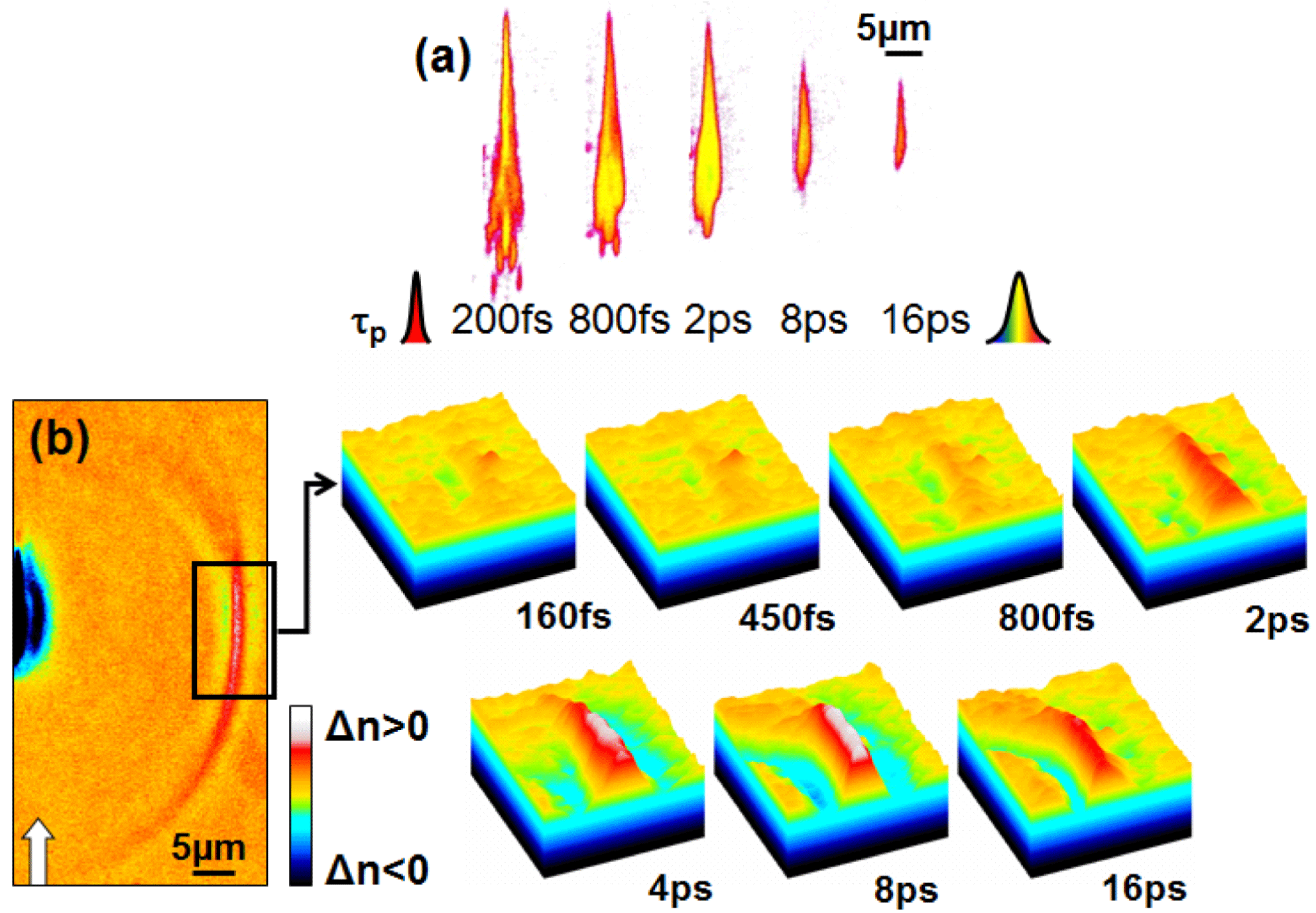
Figure 7. (a) Excitation increase (absorption maps in false colors) upon irradiation with pulses of increasing duration. (b) Pressure wave magnitude dependence in fused silica on the input pulse duration for an energy of $4~\unicode[STIX]{x03BC}\text{J}$ . The color bar indicates relative positive and negative transient refractive index changes associated to thermomechanical phenomena.