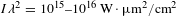1 Introduction
Laser energy absorption in plasma shows two opposite trends, depending on the laser intensity. The absorption coefficient decreases with the laser intensity in the nonrelativistic domain for laser irradiances in the range
![]() $10^{12}$
–
$10^{12}$
–
![]() $10^{16}~\text{W}\,\cdot \,\unicode[STIX]{x03BC}\text{m}^{2}/\text{cm}^{2}$
, which is explained by the increase of the plasma temperature and decrease of the electron–ion collision frequency[Reference Garban-Labaune, Fabre, Max, Fabbro, Amiranoff, Virmont, Weinfeld and Michard1]. In contrast, at relativistic irradiances, above
$10^{16}~\text{W}\,\cdot \,\unicode[STIX]{x03BC}\text{m}^{2}/\text{cm}^{2}$
, which is explained by the increase of the plasma temperature and decrease of the electron–ion collision frequency[Reference Garban-Labaune, Fabre, Max, Fabbro, Amiranoff, Virmont, Weinfeld and Michard1]. In contrast, at relativistic irradiances, above
![]() $10^{18}~\text{W}\,\cdot \,\unicode[STIX]{x03BC}\text{m}^{2}/\text{cm}^{2}$
, the efficiency of laser energy deposition in plasma increases due to resonant plasma wave excitation and strong coupling to electrons at a steepened density profile[Reference Nilson, Solodov, Myatt, Theobald, Jaanimagi, Gao, Stoeckl, Craxton, Delettrez, Yaakobi, Zuegel, Kruschwitz, Dorrer, Kelly, Akli, Patel, Mackinnon, Betti, Sangster and Meyerhofer2]. The domain of intermediate irradiances between
$10^{18}~\text{W}\,\cdot \,\unicode[STIX]{x03BC}\text{m}^{2}/\text{cm}^{2}$
, the efficiency of laser energy deposition in plasma increases due to resonant plasma wave excitation and strong coupling to electrons at a steepened density profile[Reference Nilson, Solodov, Myatt, Theobald, Jaanimagi, Gao, Stoeckl, Craxton, Delettrez, Yaakobi, Zuegel, Kruschwitz, Dorrer, Kelly, Akli, Patel, Mackinnon, Betti, Sangster and Meyerhofer2]. The domain of intermediate irradiances between
![]() $10^{15}$
and
$10^{15}$
and
![]() $10^{18}~\text{W}\,\cdot \,\unicode[STIX]{x03BC}\text{m}^{2}/\text{cm}^{2}$
is much less studied. It was demonstrated that, at the lower limit of this domain, collisional absorption decreases and is replaced by collective effects – in particular, by stimulated Raman scattering (SRS)[Reference Klimo, Tikhonchuk, Ribeyre, Schurtz, Riconda, Weber and Limpouch3]. However, the details of the collisionless absorption process were not sufficiently discussed and the simulations were performed for a rather short laser wavelength
$10^{18}~\text{W}\,\cdot \,\unicode[STIX]{x03BC}\text{m}^{2}/\text{cm}^{2}$
is much less studied. It was demonstrated that, at the lower limit of this domain, collisional absorption decreases and is replaced by collective effects – in particular, by stimulated Raman scattering (SRS)[Reference Klimo, Tikhonchuk, Ribeyre, Schurtz, Riconda, Weber and Limpouch3]. However, the details of the collisionless absorption process were not sufficiently discussed and the simulations were performed for a rather short laser wavelength
![]() $\unicode[STIX]{x1D706}=0.35~\unicode[STIX]{x03BC}\text{m}$
, and therefore for relatively low irradiances
$\unicode[STIX]{x1D706}=0.35~\unicode[STIX]{x03BC}\text{m}$
, and therefore for relatively low irradiances
![]() $I\unicode[STIX]{x1D706}^{2}<10^{15}~\text{W}\,\cdot \,\unicode[STIX]{x03BC}\text{m}^{2}/\text{cm}^{2}$
.
$I\unicode[STIX]{x1D706}^{2}<10^{15}~\text{W}\,\cdot \,\unicode[STIX]{x03BC}\text{m}^{2}/\text{cm}^{2}$
.
Parametric processes in a hot, large-scale plasma have been studied in Refs. [Reference Hinkel, Haan, Langdon, Dittrich, Still and Marinak4, Reference Xiao, Liu, Zheng and He5] for parameters relevant for indirect inertial confinement fusion experiments, and also for lower irradiances than we are interested in here. Collisionless laser energy absorption due to resonance excitation of large-amplitude plasma waves was reported in Ref. [Reference Estabrook, Valeo and Kruer6], but this study was limited to very steep plasma density profiles where parametric instabilities are suppressed. In future experiments with more intense laser pulses and longer wavelengths, nonlinear and collisionless processes will certainly be important. This domain of laser and plasma parameters is also of interest for various applications of high-power lasers, in particular, the shock ignition scheme of inertial confinement fusion targets[Reference Batani, Baton, Casner, Depierreux, Hohenberger, Klimo, Koenig, Labaune, Ribeyre, Rousseaux, Schurtz, Theobald and Tikhonchuk7].
This paper presents results of laser–plasma interaction studies in the domain of high irradiances
![]() $I\unicode[STIX]{x1D706}^{2}=10^{15}{-}10^{16}~\text{W}\,\cdot \,\unicode[STIX]{x03BC}\text{m}^{2}/\text{cm}^{2}$
and at normal incidence of the laser on a planar inhomogeneous expanding plasma. The theoretical and numerical analysis is related to the experiment[Reference Batani, Antonelli, Barbato, Boutoux, Colaïtis, Feugeas, Folpini, Mancelli, Nicolaï, Santos, Trela, Tikhonchuk, Badziak, Chodukowski, Jakubowska, Kalinowska, Pisarczyk, Rosinski, Sawicka, Baffigi, Cristoforetti, D’Amato, Koester, Gizzi, Viciani, Atzeni, Sciavi, Skoric, Gu’skov, Honrubia, Limpouch, Klimo, Skala, Gu, Krousky, Renner, Smid, Weber, Dudzak, Krus and Ullschmied8] performed on the PALS laser system in Prague[Reference Jungwirth, Cejnarova, Juha, Kralikova, Krasa, Krousky, Krupickova, Laska, Masek, Mocek, Pfeifer, Präg, Renner, Rohlena, Rus, Skala, Straka and Ullschmied9]. The laser delivers up to 700 J in a 350 ps pulse at a wavelength of
$I\unicode[STIX]{x1D706}^{2}=10^{15}{-}10^{16}~\text{W}\,\cdot \,\unicode[STIX]{x03BC}\text{m}^{2}/\text{cm}^{2}$
and at normal incidence of the laser on a planar inhomogeneous expanding plasma. The theoretical and numerical analysis is related to the experiment[Reference Batani, Antonelli, Barbato, Boutoux, Colaïtis, Feugeas, Folpini, Mancelli, Nicolaï, Santos, Trela, Tikhonchuk, Badziak, Chodukowski, Jakubowska, Kalinowska, Pisarczyk, Rosinski, Sawicka, Baffigi, Cristoforetti, D’Amato, Koester, Gizzi, Viciani, Atzeni, Sciavi, Skoric, Gu’skov, Honrubia, Limpouch, Klimo, Skala, Gu, Krousky, Renner, Smid, Weber, Dudzak, Krus and Ullschmied8] performed on the PALS laser system in Prague[Reference Jungwirth, Cejnarova, Juha, Kralikova, Krasa, Krousky, Krupickova, Laska, Masek, Mocek, Pfeifer, Präg, Renner, Rohlena, Rus, Skala, Straka and Ullschmied9]. The laser delivers up to 700 J in a 350 ps pulse at a wavelength of
![]() $1.315~\unicode[STIX]{x03BC}\text{m}$
. By focusing the pulse in a
$1.315~\unicode[STIX]{x03BC}\text{m}$
. By focusing the pulse in a
![]() $100~\unicode[STIX]{x03BC}\text{m}$
spot at a flat solid target, one obtains intensities above
$100~\unicode[STIX]{x03BC}\text{m}$
spot at a flat solid target, one obtains intensities above
![]() $2\times 10^{16}~\text{W}/\text{cm}^{2}$
, resulting in strongly nonlinear phenomena such as broadband scattered radiation and fluxes of energetic electrons. While this paper does not aim at a detailed interpretation of experimental data, we consider the experimental parameters as representative for such a regime of interaction, and use them for our detailed studies of interaction physics. By performing extended two-dimensional particle-in-cell (PIC) numerical simulations we characterize the amount of laser energy reflected and absorbed in the plasma, the spectrum of reflected light, and the energy distribution of electrons carrying absorbed energy into denser plasma beyond the critical layer. Moreover, by analyzing the spatial and spectral distribution of plasma charge and density fluctuations, we identify the processes responsible for scattering and absorption of laser energy and its redistribution in the plasma. It is demonstrated that SRS near the quarter critical density is the dominant process responsible for the laser energy absorption, while stimulated Brillouin scattering (SBS), operating in lower-density plasma layers, creates a significant amount of reflected light.
$2\times 10^{16}~\text{W}/\text{cm}^{2}$
, resulting in strongly nonlinear phenomena such as broadband scattered radiation and fluxes of energetic electrons. While this paper does not aim at a detailed interpretation of experimental data, we consider the experimental parameters as representative for such a regime of interaction, and use them for our detailed studies of interaction physics. By performing extended two-dimensional particle-in-cell (PIC) numerical simulations we characterize the amount of laser energy reflected and absorbed in the plasma, the spectrum of reflected light, and the energy distribution of electrons carrying absorbed energy into denser plasma beyond the critical layer. Moreover, by analyzing the spatial and spectral distribution of plasma charge and density fluctuations, we identify the processes responsible for scattering and absorption of laser energy and its redistribution in the plasma. It is demonstrated that SRS near the quarter critical density is the dominant process responsible for the laser energy absorption, while stimulated Brillouin scattering (SBS), operating in lower-density plasma layers, creates a significant amount of reflected light.
The paper is organized as follows. Section 2 describes the methodology of the work and the numerical tools. Section 3 contains the major results concerning the energy balance in the plasma, characteristics of scattered radiation, and spatial and energy distribution of electron fluxes. Section 4 is dedicated to the analysis of physical processes responsible for laser energy absorption and scattering. Finally, Section 5 discusses the results and presents our conclusions.
Table 1. Input laser and plasma parameters used in modeling of nonlinear interaction processes.

2 Methodology
The interaction conditions for the PALS experiment have been modeled with the radiation hydrodynamic code CHIC[Reference Breil, Galera and Maire10] and the plasma corona has been characterized by four parameters: the laser intensity in the center of the focal spot
![]() $I_{\text{las}}$
, the density scale length
$I_{\text{las}}$
, the density scale length
![]() $L_{n}$
at the quarter critical density by assuming an exponential density profile
$L_{n}$
at the quarter critical density by assuming an exponential density profile
![]() $n_{e}(x)=n_{c}\,\exp (x/L_{n})$
along the target normal, and the electron and ion temperatures,
$n_{e}(x)=n_{c}\,\exp (x/L_{n})$
along the target normal, and the electron and ion temperatures,
![]() $T_{e}$
and
$T_{e}$
and
![]() $T_{i}$
, respectively. These parameters are presented in Table 1. The critical electron plasma density (
$T_{i}$
, respectively. These parameters are presented in Table 1. The critical electron plasma density (
![]() $n_{c}=\unicode[STIX]{x1D716}_{0}m_{e}\unicode[STIX]{x1D714}_{0}/e^{2}$
,
$n_{c}=\unicode[STIX]{x1D716}_{0}m_{e}\unicode[STIX]{x1D714}_{0}/e^{2}$
,
![]() $\unicode[STIX]{x1D714}_{0}=2\unicode[STIX]{x1D70B}c/\unicode[STIX]{x1D706}_{0}$
) is
$\unicode[STIX]{x1D714}_{0}=2\unicode[STIX]{x1D70B}c/\unicode[STIX]{x1D706}_{0}$
) is
![]() $6.4\times 10^{20}~\text{cm}^{-3}$
for a laser wavelength of
$6.4\times 10^{20}~\text{cm}^{-3}$
for a laser wavelength of
![]() $\unicode[STIX]{x1D706}_{0}=1.315~\unicode[STIX]{x03BC}\text{m}$
. Here,
$\unicode[STIX]{x1D706}_{0}=1.315~\unicode[STIX]{x03BC}\text{m}$
. Here,
![]() $e$
is the elementary charge,
$e$
is the elementary charge,
![]() $m_{e}$
is the electron mass and
$m_{e}$
is the electron mass and
![]() $\unicode[STIX]{x1D716}_{0}$
is the vacuum dielectric permittivity. The plastic (CH) plasma is represented as a mixture of electrons and single-ion species with charge
$\unicode[STIX]{x1D716}_{0}$
is the vacuum dielectric permittivity. The plastic (CH) plasma is represented as a mixture of electrons and single-ion species with charge
![]() $Z=3.5$
and atomic mass
$Z=3.5$
and atomic mass
![]() $A=6.5$
. The temporal profile of the laser pulse is shown in Figure 1(a), with the circles indicating the five representative points. It has a bell-like shape with slower descending slope and a full-width at half-maximum (FWHM) of 350 ps. Time
$A=6.5$
. The temporal profile of the laser pulse is shown in Figure 1(a), with the circles indicating the five representative points. It has a bell-like shape with slower descending slope and a full-width at half-maximum (FWHM) of 350 ps. Time
![]() $t_{p}=0$
corresponds to the pulse maximum. The plasma scale length and temperatures are asymmetric; they increase with time to the end of the laser pulse because of plasma heating and expansion. The temperature decreases in the end.
$t_{p}=0$
corresponds to the pulse maximum. The plasma scale length and temperatures are asymmetric; they increase with time to the end of the laser pulse because of plasma heating and expansion. The temperature decreases in the end.
The radiation hydrodynamic code CHIC [Reference Breil, Galera and Maire10] includes two-dimensional axially symmetric hydrodynamics with ion and classical or nonlocal electron heat conduction, thermal coupling of electrons and ions, and detailed radiation transport. The laser propagation is described in the paraxial complex geometrical optics approximation[Reference Colaïtis, Duchateau, Nicolaï and Tikhonchuk11], coupled to simplified models of resonance absorption and hot electron generation due to the two-plasmon decay (TPD) and SRS[Reference Colaïtis, Duchateau, Ribeyre, Maheut, Boutoux, Antonelli, Nicolaï, Batani and Tikhonchuk12]. These nonlinear features of the laser–plasma interaction model have been tested in experiments with short wavelength lasers (
![]() $0.35~\unicode[STIX]{x03BC}\text{m}$
) and at low laser irradiances
$0.35~\unicode[STIX]{x03BC}\text{m}$
) and at low laser irradiances
![]() $I\unicode[STIX]{x1D706}^{2}\leqslant 10^{15}~\text{W}\,\cdot \,\unicode[STIX]{x03BC}\text{m}^{2}/\text{cm}^{2}$
. We do not expect it to be sufficiently predictive for the conditions we are interested in here. The plasma parameters calculated with CHIC are considered as a first approximation for the plasma density profiles and temperatures, which are modified subsequently by the PIC simulations.
$I\unicode[STIX]{x1D706}^{2}\leqslant 10^{15}~\text{W}\,\cdot \,\unicode[STIX]{x03BC}\text{m}^{2}/\text{cm}^{2}$
. We do not expect it to be sufficiently predictive for the conditions we are interested in here. The plasma parameters calculated with CHIC are considered as a first approximation for the plasma density profiles and temperatures, which are modified subsequently by the PIC simulations.

Figure 1. (a) The pulse shape and the selected representative points for the kinetic simulations. (b) Typical filamentation structure observed in our simulations and represented by the electron density distribution at the time corresponding to the laser pulse maximum in panel (a).
Kinetic simulations are performed with the relativistic electromagnetic code EPOCH[Reference Arber, Bennett, Brady, Lawrence-Douglas, Ramsay, Sircombe, Gillies, Evans, Schmitz, Bell and Ridgers13] in a planar two-dimensional geometry in the p-polarization plane (laser electric field in the plane of simulation). Absorbing boundary conditions are applied for the electromagnetic fields, and particles are thermalized to prevent the hot return currents. The simulation box size in the transverse direction with respect to the laser propagation is
![]() $l_{y}=65~\unicode[STIX]{x03BC}\text{m}$
. It is sufficiently large to allow filamentation of the laser beam and the development of multiple filaments.
$l_{y}=65~\unicode[STIX]{x03BC}\text{m}$
. It is sufficiently large to allow filamentation of the laser beam and the development of multiple filaments.
The condition for the threshold wavelength modes of the filamentation instability is given by Ref. [Reference Kruer14]:
![]() $(\unicode[STIX]{x1D706}_{0}/l_{y})^{2}\leqslant (\unicode[STIX]{x1D714}_{pe}/\unicode[STIX]{x1D714}_{0})^{2}(v_{\text{osc}}/v_{e})^{2}/2$
, where
$(\unicode[STIX]{x1D706}_{0}/l_{y})^{2}\leqslant (\unicode[STIX]{x1D714}_{pe}/\unicode[STIX]{x1D714}_{0})^{2}(v_{\text{osc}}/v_{e})^{2}/2$
, where
![]() $\unicode[STIX]{x1D714}_{pe}=(e^{2}n_{e}/m_{e}\unicode[STIX]{x1D716}_{0})^{1/2}$
is the plasma frequency,
$\unicode[STIX]{x1D714}_{pe}=(e^{2}n_{e}/m_{e}\unicode[STIX]{x1D716}_{0})^{1/2}$
is the plasma frequency,
![]() $v_{\text{osc}}=eE_{\text{las}}/m_{e}\unicode[STIX]{x1D714}_{0}$
is the electron quiver velocity,
$v_{\text{osc}}=eE_{\text{las}}/m_{e}\unicode[STIX]{x1D714}_{0}$
is the electron quiver velocity,
![]() $E_{\text{las}}=(2I_{\text{las}}/\unicode[STIX]{x1D716}_{0}c)^{1/2}$
is the laser electric field, and
$E_{\text{las}}=(2I_{\text{las}}/\unicode[STIX]{x1D716}_{0}c)^{1/2}$
is the laser electric field, and
![]() $v_{e}=(T_{e}/m_{e})^{1/2}$
is the electron thermal velocity. The typical filamentation structure observed in simulations is shown by the electron density distribution for the case of
$v_{e}=(T_{e}/m_{e})^{1/2}$
is the electron thermal velocity. The typical filamentation structure observed in simulations is shown by the electron density distribution for the case of
![]() $t_{p}=0$
in Figure 1(b). The box length in the laser propagation direction,
$t_{p}=0$
in Figure 1(b). The box length in the laser propagation direction,
![]() $l_{x}\,\sim \,150{-}450~\unicode[STIX]{x03BC}\text{m}$
, was chosen 5–8 times larger than the corresponding density scale length given in Table 1 so as to cover the range of plasma densities from
$l_{x}\,\sim \,150{-}450~\unicode[STIX]{x03BC}\text{m}$
, was chosen 5–8 times larger than the corresponding density scale length given in Table 1 so as to cover the range of plasma densities from
![]() $0.01n_{c}$
to
$0.01n_{c}$
to
![]() $n_{c}$
with additional margins from both sides where the transmitted and reflected fluxes have been calculated. The mesh resolution
$n_{c}$
with additional margins from both sides where the transmitted and reflected fluxes have been calculated. The mesh resolution
![]() $\unicode[STIX]{x1D6FF}x=\unicode[STIX]{x1D6FF}y=0.02\,\unicode[STIX]{x1D706}_{0}$
is chosen to resolve the Debye length. The corresponding time step is
$\unicode[STIX]{x1D6FF}x=\unicode[STIX]{x1D6FF}y=0.02\,\unicode[STIX]{x1D706}_{0}$
is chosen to resolve the Debye length. The corresponding time step is
![]() $\unicode[STIX]{x1D6FF}t=0.08\,\unicode[STIX]{x1D714}_{0}^{-1}$
. The laser in each simulation is assumed to be a plane wave with a 1 ps rise time following a constant intensity given in Table 1. In the experiment, the laser intensity distribution may have fluctuations – so-called hot spots which influence the onset of filamentation. However, in the conditions considered here, the laser power significantly exceeds the threshold of the ponderomotive self-focusing
$\unicode[STIX]{x1D6FF}t=0.08\,\unicode[STIX]{x1D714}_{0}^{-1}$
. The laser in each simulation is assumed to be a plane wave with a 1 ps rise time following a constant intensity given in Table 1. In the experiment, the laser intensity distribution may have fluctuations – so-called hot spots which influence the onset of filamentation. However, in the conditions considered here, the laser power significantly exceeds the threshold of the ponderomotive self-focusing
![]() $P_{cr}\approx 0.034T_{e,\text{keV}}(n_{c}/n_{e})\text{(GW)}$
. Assuming the filaments occur above
$P_{cr}\approx 0.034T_{e,\text{keV}}(n_{c}/n_{e})\text{(GW)}$
. Assuming the filaments occur above
![]() $0.1n_{c}$
, and for the plasma temperature
$0.1n_{c}$
, and for the plasma temperature
![]() $T_{e}\sim 3~\text{keV}$
, the corresponding critical power will be
$T_{e}\sim 3~\text{keV}$
, the corresponding critical power will be
![]() $P_{cr}\approx 1~\text{GW}$
. For a typical speckle size in the PALS experiment of
$P_{cr}\approx 1~\text{GW}$
. For a typical speckle size in the PALS experiment of
![]() ${\sim}5~\unicode[STIX]{x03BC}\text{m}$
and an intensity
${\sim}5~\unicode[STIX]{x03BC}\text{m}$
and an intensity
![]() $2\times 10^{16}~\text{W}/\text{cm}^{2}$
, the average speckle power is
$2\times 10^{16}~\text{W}/\text{cm}^{2}$
, the average speckle power is
![]() ${\sim}30~\text{GW}$
; that is, more than an order of magnitude larger than the critical power. Therefore, in our case the overall laser field is well above the filamentation threshold and the intensity fluctuations due to the hot spots will not be so important. In realistic laser beams with a speckle structure, intense speckles with
${\sim}30~\text{GW}$
; that is, more than an order of magnitude larger than the critical power. Therefore, in our case the overall laser field is well above the filamentation threshold and the intensity fluctuations due to the hot spots will not be so important. In realistic laser beams with a speckle structure, intense speckles with
![]() $P/P_{cr}$
much greater than one may occur and affect the onset of both SBS and filamentation of the average beam treated by the current study.
$P/P_{cr}$
much greater than one may occur and affect the onset of both SBS and filamentation of the average beam treated by the current study.
Each simulation was performed for about 10 ps until a quasistationary state had been reached. The results from the quasi-steady phase of the interaction can be compared with the corresponding macroscopic data. The PIC simulation starts with the temperature and density profiles originating from the hydrodynamic simulations, but with uniform density and intensity distributions in the transverse direction. Although it is not fully self-consistent, we found that the filamentation always appears in the initial stage when the laser intensity profile is growing, as shown in Figure 1(b). Therefore, when the stationary state is reached, the filamentation structures in all cases are similar and the initial uniform transverse density distribution is modified. The characteristic expansion velocity in the hydrodynamic simulation is about
![]() $1~\unicode[STIX]{x03BC}\text{m}/\text{ps}$
. The corresponding plasma profile variation is negligible in the simulation time of less than 10 ps. The characteristic velocity gradient length is about
$1~\unicode[STIX]{x03BC}\text{m}/\text{ps}$
. The corresponding plasma profile variation is negligible in the simulation time of less than 10 ps. The characteristic velocity gradient length is about
![]() $L_{v}\sim 160~\unicode[STIX]{x03BC}\text{m}$
– more than hundred times larger than the laser wavelength. The condition for the net growth of SBS can be written as
$L_{v}\sim 160~\unicode[STIX]{x03BC}\text{m}$
– more than hundred times larger than the laser wavelength. The condition for the net growth of SBS can be written as
![]() $(v_{\text{osc}}/v_{e})^{2}>(8/k_{0}L_{v})(2\unicode[STIX]{x1D714}_{0}^{2}/\unicode[STIX]{x1D714}_{pe}^{2})$
. The effect of velocity gradient length on the SBS growth rate is very small, as the electron quiver velocity is of the order of the electron thermal velocity. For the laser intensities of the particular PALS experiment, SBS takes place in the strongly coupled regime so that the presence of the sonic point for plasma expansion is not important for the spectrum of the reflected light. For these reasons the plasma expansion velocity was not accounted for in the simulation.
$(v_{\text{osc}}/v_{e})^{2}>(8/k_{0}L_{v})(2\unicode[STIX]{x1D714}_{0}^{2}/\unicode[STIX]{x1D714}_{pe}^{2})$
. The effect of velocity gradient length on the SBS growth rate is very small, as the electron quiver velocity is of the order of the electron thermal velocity. For the laser intensities of the particular PALS experiment, SBS takes place in the strongly coupled regime so that the presence of the sonic point for plasma expansion is not important for the spectrum of the reflected light. For these reasons the plasma expansion velocity was not accounted for in the simulation.
In Ref. [Reference Cui, Wang, Sheng and Li15], Cui et al. concluded that the collisional absorption becomes less significant when the laser intensity is close to
![]() $10^{16}~\text{W}\,\cdot \,\unicode[STIX]{x03BC}\text{m}^{2}/\text{cm}^{2}$
, as the plasma temperature is rather high. This observation agrees with our hydrodynamics simulation predicting the collisional absorption to be less than 9%. The collisions are thus neglected in numerical simulations, as we are interested in the demonstration of nonlinear laser absorption. In what follows the lengths are given in units of the laser wavelength
$10^{16}~\text{W}\,\cdot \,\unicode[STIX]{x03BC}\text{m}^{2}/\text{cm}^{2}$
, as the plasma temperature is rather high. This observation agrees with our hydrodynamics simulation predicting the collisional absorption to be less than 9%. The collisions are thus neglected in numerical simulations, as we are interested in the demonstration of nonlinear laser absorption. In what follows the lengths are given in units of the laser wavelength
![]() $\unicode[STIX]{x1D706}_{0}=1.315~\unicode[STIX]{x03BC}\text{m}$
and the time in picoseconds.
$\unicode[STIX]{x1D706}_{0}=1.315~\unicode[STIX]{x03BC}\text{m}$
and the time in picoseconds.
3 Energy balance in laser–plasma interactions
The interaction process enters after 5–6 ps into a quasistationary regime where the internal energy in the simulation box remains approximately constant. Only this asymptotic stage of each simulation interval is analyzed in what follows. The outgoing energy balance averaged over the last 1 ps of simulation is presented in Table 2. The energy flux through the left boundary is made up of backscattered and reflected electromagnetic waves. The contributions of SRS and SBS have been separated by the spectral filtering. Both processes are based on the three-wave coupling mechanism and matching the conditions of energy conservation,
![]() $\unicode[STIX]{x1D714}_{0}=\unicode[STIX]{x1D714}_{1}+\unicode[STIX]{x1D714}_{s}$
, and momentum conservation,
$\unicode[STIX]{x1D714}_{0}=\unicode[STIX]{x1D714}_{1}+\unicode[STIX]{x1D714}_{s}$
, and momentum conservation,
![]() $\mathbf{k}_{p0}=\mathbf{k}_{p1}+\mathbf{k}_{s}$
. Here,
$\mathbf{k}_{p0}=\mathbf{k}_{p1}+\mathbf{k}_{s}$
. Here,
![]() $\unicode[STIX]{x1D714}_{s}$
and
$\unicode[STIX]{x1D714}_{s}$
and
![]() $\mathbf{k}_{s}$
signify the frequency and wavevector of the plasma response as the electron plasma wave (EPW) and ion acoustic wave (IAW) for SRS and SBS cases, respectively. As the electron plasma frequency is comparable to the light frequency, SRS corresponds to large frequency shifts (typically larger than
$\mathbf{k}_{s}$
signify the frequency and wavevector of the plasma response as the electron plasma wave (EPW) and ion acoustic wave (IAW) for SRS and SBS cases, respectively. As the electron plasma frequency is comparable to the light frequency, SRS corresponds to large frequency shifts (typically larger than
![]() $0.1\unicode[STIX]{x1D714}_{0}$
). It was separated from SBS by spectral filtering of backscattered light with
$0.1\unicode[STIX]{x1D714}_{0}$
). It was separated from SBS by spectral filtering of backscattered light with
![]() $\unicode[STIX]{x1D714}<0.9\unicode[STIX]{x1D714}_{0}$
. Backscattered light with smaller frequency shifts (
$\unicode[STIX]{x1D714}<0.9\unicode[STIX]{x1D714}_{0}$
. Backscattered light with smaller frequency shifts (
![]() $0.9<\unicode[STIX]{x1D714}/\unicode[STIX]{x1D714}_{0}<1.1$
) was attributed to SBS. The energy flux through the transverse boundaries is also made up of electromagnetic waves. It is verified that the Poynting vector has a normal component to the boundaries near the transverse sides of the simulation box and a sign corresponding to the outgoing waves. The sidescattering is defined as the field detected on the transverse boundaries (
$0.9<\unicode[STIX]{x1D714}/\unicode[STIX]{x1D714}_{0}<1.1$
) was attributed to SBS. The energy flux through the transverse boundaries is also made up of electromagnetic waves. It is verified that the Poynting vector has a normal component to the boundaries near the transverse sides of the simulation box and a sign corresponding to the outgoing waves. The sidescattering is defined as the field detected on the transverse boundaries (
![]() $y=\pm 65~\unicode[STIX]{x03BC}\text{m}$
). Repartition between the back- and sidescattering in our simulations is related to the aspect ratio of the box
$y=\pm 65~\unicode[STIX]{x03BC}\text{m}$
). Repartition between the back- and sidescattering in our simulations is related to the aspect ratio of the box
![]() $l_{y}/l_{x}$
. A fraction of the scattered waves are crossing the transverse box boundaries and are not detected by the backscattering diagnostics. For this reason both back and sidescattered waves are considered together while evaluating the reflected laser energy.
$l_{y}/l_{x}$
. A fraction of the scattered waves are crossing the transverse box boundaries and are not detected by the backscattering diagnostics. For this reason both back and sidescattered waves are considered together while evaluating the reflected laser energy.

Figure 2. (a) Dependence of the longitudinal component of the electron energy flux
![]() $F_{x}$
(Equation (1)) on the plasma density averaged over the transverse coordinate and the last 1 ps of the simulation time. The electron energy flux is normalized to the instantaneous incident laser energy flux
$F_{x}$
(Equation (1)) on the plasma density averaged over the transverse coordinate and the last 1 ps of the simulation time. The electron energy flux is normalized to the instantaneous incident laser energy flux
![]() $F_{\text{las}}(t_{p})$
. (b) Electron density profiles in the expanding plasmas used in PIC simulations. The five lines in both panels correspond to the pulse time
$F_{\text{las}}(t_{p})$
. (b) Electron density profiles in the expanding plasmas used in PIC simulations. The five lines in both panels correspond to the pulse time
![]() $t_{p}$
given in Table 1: black
$t_{p}$
given in Table 1: black
![]() $t_{p}=-200$
ps, blue
$t_{p}=-200$
ps, blue
![]() $t_{p}=-100$
ps, red
$t_{p}=-100$
ps, red
![]() $t_{p}=0$
, green
$t_{p}=0$
, green
![]() $t_{p}=100$
ps and pink
$t_{p}=100$
ps and pink
![]() $t_{p}=200$
ps.
$t_{p}=200$
ps.
Table 2. Energy balance in the simulation box observed in PIC simulations.

It follows from Table 2 that the dominant part of scattered energy is carried by a weakly frequency-shifted light. Further analysis confirms that this has to be attributed to the specular reflection and SBS. This fraction of scattered light gradually decreases from 95% at the beginning of laser pulse, where the reflection from the critical density dominates, to approximately 80% at the laser pulse maximum, where SBS dominates. The contribution of the strongly shifted light is relatively small and reaches barely 3%–4% at the laser pulse maximum.
The transmitted energy flux beyond the critical density is carried by the thermal and suprathermal electrons. In the quasistationary state, that electron energy flux is equal to the absorbed laser energy flux. As demonstrated in Table 2, the suprathermal electrons have an average energy which is 10 times larger than the plasma temperature. The origin of these hot electrons is identified in Figure 2. Panel (a) shows the dependence of the longitudinal component of the electron energy flux
![]() $F_{x}$
on the plasma density integrated over the transverse direction. Here, the electron energy flux
$F_{x}$
on the plasma density integrated over the transverse direction. Here, the electron energy flux
![]() $F_{ex}$
is defined as
$F_{ex}$
is defined as
 $$\begin{eqnarray}\displaystyle F_{ex}(x) & = & \displaystyle \int \text{d}y\int \text{d}^{3}p\,f_{e}(\mathbf{p},x)\,\unicode[STIX]{x1D700}\,v_{x}\nonumber\\ \displaystyle & = & \displaystyle 2\unicode[STIX]{x1D70B}\int \text{d}y\int _{0}^{\infty }\text{d}\unicode[STIX]{x1D700}\,p^{2}\unicode[STIX]{x1D700}\nonumber\\ \displaystyle & & \displaystyle \times \,\int _{0}^{\unicode[STIX]{x1D70B}}\text{d}\unicode[STIX]{x1D703}\,\sin \unicode[STIX]{x1D703}\,\cos \unicode[STIX]{x1D703}\,f_{e}(\unicode[STIX]{x1D700},\unicode[STIX]{x1D703},x),\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle F_{ex}(x) & = & \displaystyle \int \text{d}y\int \text{d}^{3}p\,f_{e}(\mathbf{p},x)\,\unicode[STIX]{x1D700}\,v_{x}\nonumber\\ \displaystyle & = & \displaystyle 2\unicode[STIX]{x1D70B}\int \text{d}y\int _{0}^{\infty }\text{d}\unicode[STIX]{x1D700}\,p^{2}\unicode[STIX]{x1D700}\nonumber\\ \displaystyle & & \displaystyle \times \,\int _{0}^{\unicode[STIX]{x1D70B}}\text{d}\unicode[STIX]{x1D703}\,\sin \unicode[STIX]{x1D703}\,\cos \unicode[STIX]{x1D703}\,f_{e}(\unicode[STIX]{x1D700},\unicode[STIX]{x1D703},x),\end{eqnarray}$$
where
![]() $f_{e}$
is the electron distribution function,
$f_{e}$
is the electron distribution function,
![]() $\unicode[STIX]{x1D703}$
is the polar angle of electron momentum
$\unicode[STIX]{x1D703}$
is the polar angle of electron momentum
![]() $\mathbf{p}$
with respect to the laser propagation axis
$\mathbf{p}$
with respect to the laser propagation axis
![]() $x$
, and
$x$
, and
![]() $\unicode[STIX]{x1D700}$
is the electron energy. The five lines in this panel correspond to the simulations with five values of the laser intensity given in Table 1. The curves are normalized to the instantaneous incident laser flux
$\unicode[STIX]{x1D700}$
is the electron energy. The five lines in this panel correspond to the simulations with five values of the laser intensity given in Table 1. The curves are normalized to the instantaneous incident laser flux
![]() $F_{\text{las}}(t_{p})=I_{\text{las}}(t_{p})l_{y}$
. There are three clearly different parts in this plot. The electron energy flux is almost zero in the density range below
$F_{\text{las}}(t_{p})=I_{\text{las}}(t_{p})l_{y}$
. There are three clearly different parts in this plot. The electron energy flux is almost zero in the density range below
![]() $n_{e}\simeq 0.2n_{c}$
. This means that there is no notable coupling of laser energy to the plasma. A dramatic increase of the electron energy flux occurs near the quarter critical density in a density interval
$n_{e}\simeq 0.2n_{c}$
. This means that there is no notable coupling of laser energy to the plasma. A dramatic increase of the electron energy flux occurs near the quarter critical density in a density interval
![]() $(0.2{-}0.3)n_{c}$
. At early times
$(0.2{-}0.3)n_{c}$
. At early times
![]() $t_{p}=-200$
and
$t_{p}=-200$
and
![]() $-100$
ps there is also a notable increase of the electron flux in the region before the critical density,
$-100$
ps there is also a notable increase of the electron flux in the region before the critical density,
![]() $(0.85{-}0.95)n_{c}$
, but this is not the case for later times. The parametric instabilities before and at the quarter critical density lead to significant absorption of the laser energy, and only a relatively small amount of light reaches the critical density zone. However, there are no collisions included in our simulations. The observed laser energy absorption is fully nonlinear. Further analysis identifies SRS as the dominant absorption process.
$(0.85{-}0.95)n_{c}$
, but this is not the case for later times. The parametric instabilities before and at the quarter critical density lead to significant absorption of the laser energy, and only a relatively small amount of light reaches the critical density zone. However, there are no collisions included in our simulations. The observed laser energy absorption is fully nonlinear. Further analysis identifies SRS as the dominant absorption process.

Figure 3. (a) Distribution of the electron energy flux entering the overcritical plasma
![]() $n_{e}\gtrsim n_{c}$
on the parallel momentum,
$n_{e}\gtrsim n_{c}$
on the parallel momentum,
![]() $\text{d}F_{x}/\text{d}p_{x}$
. All curves are normalized to the total electron energy flux at that position. The five lines in both panels correspond to the pulse times
$\text{d}F_{x}/\text{d}p_{x}$
. All curves are normalized to the total electron energy flux at that position. The five lines in both panels correspond to the pulse times
![]() $t_{p}$
given in Table 1. The color code is the same as in Figure 2. (b) Distribution of electrons in the plasma near the critical density as a function of the energy
$t_{p}$
given in Table 1. The color code is the same as in Figure 2. (b) Distribution of electrons in the plasma near the critical density as a function of the energy
![]() $\unicode[STIX]{x1D700}$
and the polar angle
$\unicode[STIX]{x1D700}$
and the polar angle
![]() $\unicode[STIX]{x1D703}$
. The laser pulse time
$\unicode[STIX]{x1D703}$
. The laser pulse time
![]() $t_{p}=0$
and the quasi-steady phase of the simulation are considered. Color bar is in a logarithmic scale.
$t_{p}=0$
and the quasi-steady phase of the simulation are considered. Color bar is in a logarithmic scale.
The spatial extent of the zones of efficient laser energy absorption can be seen from the density profiles shown in Figure 2(b). During the PIC simulation time of 10 ps, the transversally averaged density does not change much, although there is significant small-scale modulation related to the laser filamentation. This feature is shown in Figure 1(b) and discussed in the next section. The spatial extent of the zone near the critical density where hot electrons are generated is less than
![]() $10~\unicode[STIX]{x03BC}\text{m}$
, while the spatial width of the interaction zone near the quarter critical density increases with time from
$10~\unicode[STIX]{x03BC}\text{m}$
, while the spatial width of the interaction zone near the quarter critical density increases with time from
![]() $10{-}20~\unicode[STIX]{x03BC}\text{m}$
at early times to more than
$10{-}20~\unicode[STIX]{x03BC}\text{m}$
at early times to more than
![]() $100~\unicode[STIX]{x03BC}\text{m}$
at later times. The expansion of the interaction zone explains a significant increase of energy transfer from the laser to electrons.
$100~\unicode[STIX]{x03BC}\text{m}$
at later times. The expansion of the interaction zone explains a significant increase of energy transfer from the laser to electrons.
The dependence of the outgoing electron energy flux on the parallel momentum
is shown in Figure 3(a). It is taken beyond the critical density
![]() $x>x_{c}$
in the zone where laser radiation cannot penetrate, and is normalized to the total energy flux at that position. The effective temperature of energetic electrons increases gradually with time from 48 keV at
$x>x_{c}$
in the zone where laser radiation cannot penetrate, and is normalized to the total energy flux at that position. The effective temperature of energetic electrons increases gradually with time from 48 keV at
![]() $t_{p}=-200$
ps to 62 keV and 90 keV at the two subsequent laser time moments (see Table 2 and Figure 3(a)). At the end of the laser pulse the temperatures of both the bulk and hot electrons decrease. Hydrodynamic simulations predict reasonably well the plasma state: the plasma density profile averaged over the transverse coordinate is weakly modified compared to the input profile, and the electron average plasma temperature at the end of the run shown in Table 2 is only 10%–20% higher than the input value shown in Table 1.
$t_{p}=-200$
ps to 62 keV and 90 keV at the two subsequent laser time moments (see Table 2 and Figure 3(a)). At the end of the laser pulse the temperatures of both the bulk and hot electrons decrease. Hydrodynamic simulations predict reasonably well the plasma state: the plasma density profile averaged over the transverse coordinate is weakly modified compared to the input profile, and the electron average plasma temperature at the end of the run shown in Table 2 is only 10%–20% higher than the input value shown in Table 1.
The energy flux into the dense plasma is carried by both the thermal and suprathermal (hot) electrons. In contrast, the return current,
![]() $p_{x}<0$
, is carried only by thermal electrons, which compensate the hot electrons ejected from the corona into a dense plasma. The number of hot electrons increases with time. Assuming that an energy of 50 keV (approximately 10 times the electron temperature) separates the thermal and suprathermal electrons, one can evaluate the contribution of the hot electrons to the energy transport. At the time
$p_{x}<0$
, is carried only by thermal electrons, which compensate the hot electrons ejected from the corona into a dense plasma. The number of hot electrons increases with time. Assuming that an energy of 50 keV (approximately 10 times the electron temperature) separates the thermal and suprathermal electrons, one can evaluate the contribution of the hot electrons to the energy transport. At the time
![]() $t_{p}=-200$
ps only 20% of the total energy flux is carried by electrons having energy greater than 50 keV. This fraction increases to
$t_{p}=-200$
ps only 20% of the total energy flux is carried by electrons having energy greater than 50 keV. This fraction increases to
![]() ${\sim}30$
% at the time
${\sim}30$
% at the time
![]() $-100$
ps, and in two subsequent time moments their contribution is about 65%, while it decreases to 25% at the last time moment. The angular distribution of hot electrons is shown in Figure 3(b). It is rather broad, with a characteristic opening angle of
$-100$
ps, and in two subsequent time moments their contribution is about 65%, while it decreases to 25% at the last time moment. The angular distribution of hot electrons is shown in Figure 3(b). It is rather broad, with a characteristic opening angle of
![]() ${\sim}50^{\circ }$
, which is explained by a broad angular spectrum of the plasma wave turbulence excited in the zone of laser energy absorption.
${\sim}50^{\circ }$
, which is explained by a broad angular spectrum of the plasma wave turbulence excited in the zone of laser energy absorption.
The question that arises from this analysis of the energy balance and inspection of Tables 1 and 2 is as follows. What is the major mechanism of laser energy absorption and how is this energy transferred to energetic electrons? This is obviously related to plasma wave excitation. But if SRS is indeed the dominant process, how can such a high forward energy flux exceeding 20% in the second part of the laser pulse be compared to the very low level of Raman scattered light, which is less than 5%. These issues are discussed in the next section.
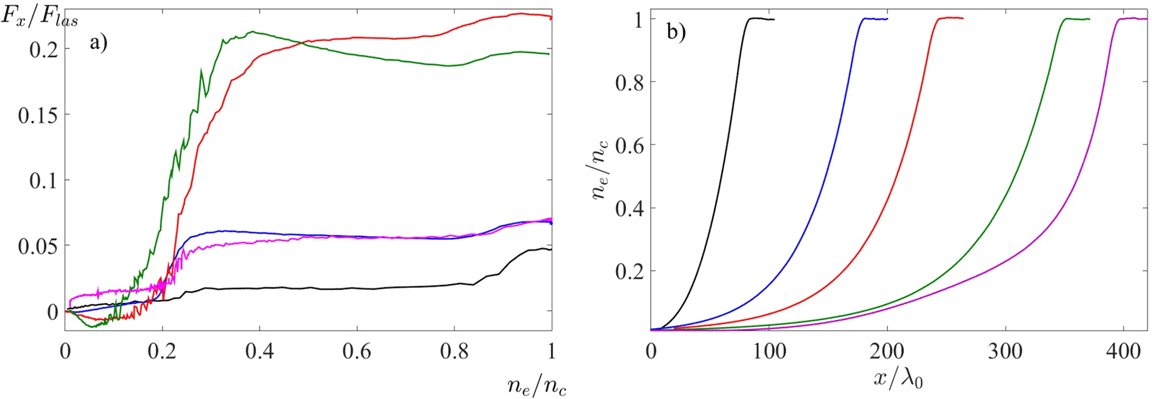
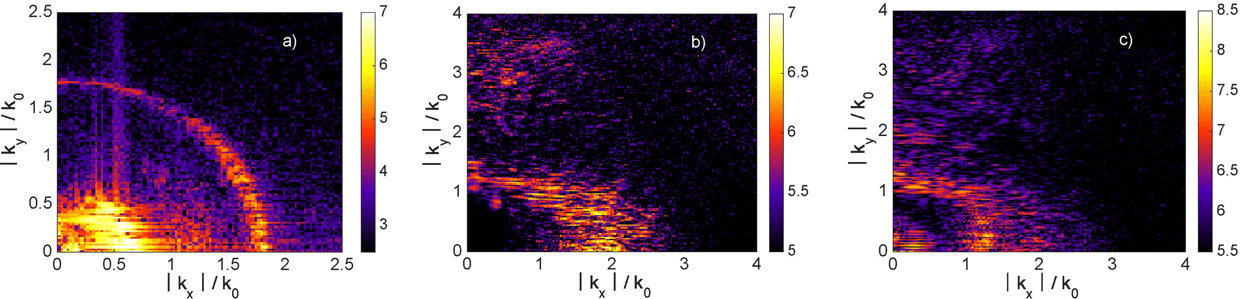
The angular distribution of the scattered light is shown in Figure 4. It presents the Fourier spectrum of the magnetic field
![]() $|B_{z}(k_{x},k_{y})|^{2}$
in the part of the simulation box where the density is smaller than the quarter critical density. As there are no hot electron energy sources in this region, here we expect to see only the incident laser wave and the outgoing scattered waves originating from denser plasma layers. Indeed, the most intense part of the Fourier spectrum corresponds to the wavevector close to
$|B_{z}(k_{x},k_{y})|^{2}$
in the part of the simulation box where the density is smaller than the quarter critical density. As there are no hot electron energy sources in this region, here we expect to see only the incident laser wave and the outgoing scattered waves originating from denser plasma layers. Indeed, the most intense part of the Fourier spectrum corresponds to the wavevector close to
![]() $k_{0}=\unicode[STIX]{x1D714}_{0}/c$
. This part is related to the incident laser and to the SBS. The scattered radiation has a quite large opening angle of about
$k_{0}=\unicode[STIX]{x1D714}_{0}/c$
. This part is related to the incident laser and to the SBS. The scattered radiation has a quite large opening angle of about
![]() $40^{\circ }{-}45^{\circ }$
. This opening angle is larger than the focusing angle of the PALS laser lens, which is about
$40^{\circ }{-}45^{\circ }$
. This opening angle is larger than the focusing angle of the PALS laser lens, which is about
![]() $15^{\circ }$
, thus implying that a significant part of the scattered light could be missed while considering only the fraction of backscattered light within the focusing lens. This opening angle is also much larger than the aspect ratio of the simulation box, which corresponds to the opening angle of
$15^{\circ }$
, thus implying that a significant part of the scattered light could be missed while considering only the fraction of backscattered light within the focusing lens. This opening angle is also much larger than the aspect ratio of the simulation box, which corresponds to the opening angle of
![]() ${\sim}10^{\circ }$
(in the case of the simulation corresponding to
${\sim}10^{\circ }$
(in the case of the simulation corresponding to
![]() $t_{p}=0$
). This fact explains our method of evaluation of the reflected laser energy by taking into account the energy fluxes through the front and side boundaries of the simulation box.
$t_{p}=0$
). This fact explains our method of evaluation of the reflected laser energy by taking into account the energy fluxes through the front and side boundaries of the simulation box.
The magnetic field Fourier spectrum also contains emission of harmonics at
![]() $\frac{3}{2}\unicode[STIX]{x1D714}_{0}$
and
$\frac{3}{2}\unicode[STIX]{x1D714}_{0}$
and
![]() $2\unicode[STIX]{x1D714}_{0}$
of the laser light and emission at frequencies lower than the laser frequency. Emissions at frequencies higher than
$2\unicode[STIX]{x1D714}_{0}$
of the laser light and emission at frequencies lower than the laser frequency. Emissions at frequencies higher than
![]() $\unicode[STIX]{x1D714}_{0}$
carry a very small fraction of the laser energy. They originate from scattering of the laser or SBS waves on the plasma waves excited near the critical and quarter critical densities. Harmonics are not important for the energy balance, but their presence confirms the plasma wave activity in these density zones.
$\unicode[STIX]{x1D714}_{0}$
carry a very small fraction of the laser energy. They originate from scattering of the laser or SBS waves on the plasma waves excited near the critical and quarter critical densities. Harmonics are not important for the energy balance, but their presence confirms the plasma wave activity in these density zones.

Figure 4. (a) Magnetic field Fourier spectrum in the part of the simulation box corresponding to the densities below the quarter critical as a function of the longitudinal and transverse components of the wavevector. Color bar is in a logarithmic scale. (The spectrum calculated from the instantaneous code output provides only the absolute values of the wavevector components.) (b) Frequency spectra of the backward propagating radiation recorded at the front boundary of the simulation box during the quasi-steady phase of interaction, for different conditions according to Table 1. The results correspond to the pulse time
![]() $t_{p}=0$
and the quasi-steady phase of the interaction. The color code is: black
$t_{p}=0$
and the quasi-steady phase of the interaction. The color code is: black
![]() $t_{p}=-200$
ps, blue
$t_{p}=-200$
ps, blue
![]() $t_{p}=-100$
ps, red
$t_{p}=-100$
ps, red
![]() $t_{p}=0$
, green
$t_{p}=0$
, green
![]() $t_{p}=100$
ps and pink
$t_{p}=100$
ps and pink
![]() $t_{p}=200$
ps.
$t_{p}=200$
ps.
The angular distribution of the low-frequency part of the scattered light shown in Figure 4(a) is directed backwards and has a much narrower opening angle, which can be captured entirely by our backscattering diagnostic. This strongly anisotropic emission is a signature of backward SRS. The spectral distribution
![]() $\unicode[STIX]{x0394}k\sim 0.3k_{0}$
is much larger than one would expect from SRS near the quarter critical plasma. This feature indicates that SRS originates from a broader density region and is accompanied by secondary processes – parametric decays, cavitation and resonance absorption – that are detailed in the next section.
$\unicode[STIX]{x0394}k\sim 0.3k_{0}$
is much larger than one would expect from SRS near the quarter critical plasma. This feature indicates that SRS originates from a broader density region and is accompanied by secondary processes – parametric decays, cavitation and resonance absorption – that are detailed in the next section.
The electromagnetic wave spectrum in the frequency domain is presented in Figure 4(b) for the radiation emitted in the backward direction and for laser pulse times varying from
![]() $-200$
ps to 200 ps. The backscattered intensity increases for some time after the laser pulse maximum, which is explained by the plasma expansion. The high-frequency part also contains emissions at
$-200$
ps to 200 ps. The backscattered intensity increases for some time after the laser pulse maximum, which is explained by the plasma expansion. The high-frequency part also contains emissions at
![]() $\frac{3}{2}\unicode[STIX]{x1D714}_{0}$
and
$\frac{3}{2}\unicode[STIX]{x1D714}_{0}$
and
![]() $2\unicode[STIX]{x1D714}_{0}$
. A significant broadening of the
$2\unicode[STIX]{x1D714}_{0}$
. A significant broadening of the
![]() $\frac{3}{2}\unicode[STIX]{x1D714}_{0}$
spectrum in the second part of laser pulse,
$\frac{3}{2}\unicode[STIX]{x1D714}_{0}$
spectrum in the second part of laser pulse,
![]() $t_{p}\geqslant 0$
, is due to extension of the SRS-driven plasma waves to densities lower than the quarter critical density. In contrast, the second-harmonic spectrum is narrow at all times and its intensity is smaller than the intensity of the harmonic
$t_{p}\geqslant 0$
, is due to extension of the SRS-driven plasma waves to densities lower than the quarter critical density. In contrast, the second-harmonic spectrum is narrow at all times and its intensity is smaller than the intensity of the harmonic
![]() $\frac{3}{2}\unicode[STIX]{x1D714}_{0}$
. This confirms a secondary role of nonlinear processes near the critical density in the laser absorption. The signals at
$\frac{3}{2}\unicode[STIX]{x1D714}_{0}$
. This confirms a secondary role of nonlinear processes near the critical density in the laser absorption. The signals at
![]() $\frac{3}{2}\unicode[STIX]{x1D714}_{0}$
and
$\frac{3}{2}\unicode[STIX]{x1D714}_{0}$
and
![]() $2\unicode[STIX]{x1D714}_{0}$
disappear at a late time of the interaction
$2\unicode[STIX]{x1D714}_{0}$
disappear at a late time of the interaction
![]() $t_{p}=200$
ps, and the SRS signal goes down by an order of magnitude. The longitudinal component of the electron energy flux indicates a strongly decreased laser absorption, which is explained by SBS developing over the extended plasma density profile.
$t_{p}=200$
ps, and the SRS signal goes down by an order of magnitude. The longitudinal component of the electron energy flux indicates a strongly decreased laser absorption, which is explained by SBS developing over the extended plasma density profile.
The particularity of the low-frequency part of the backscattered light spectrum is in increasing the signal amplitude toward lower frequencies, a double-hump maximum at half the laser frequency and an extension of the spectrum to lower frequencies at high laser intensities. While the higher-frequency part of the scattered light,
![]() $\unicode[STIX]{x1D714}>\frac{1}{2}\unicode[STIX]{x1D714}_{0}$
, can be attributed to scattering of the laser or SBS daughter wave on the SRS-driven plasma waves near or below the quarter critical density, the origins of the second lower-frequency peak and the lower-frequency wing of the spectrum are not immediately evident, and will be discussed in the next Section 4.1.
$\unicode[STIX]{x1D714}>\frac{1}{2}\unicode[STIX]{x1D714}_{0}$
, can be attributed to scattering of the laser or SBS daughter wave on the SRS-driven plasma waves near or below the quarter critical density, the origins of the second lower-frequency peak and the lower-frequency wing of the spectrum are not immediately evident, and will be discussed in the next Section 4.1.
4 Characterization of parametric instabilities
In order to identify the processes of laser absorption and hot electron production we analyze in detail the electromagnetic and plasma wave spatial distribution in particular zones near the critical and quarter critical densities by considering as a representative example the simulation corresponding to the maximum laser intensity
![]() $t_{p}=0$
.
$t_{p}=0$
.

Figure 5. (a) Fourier spectra of electromagnetic waves, (b) electron plasma waves – charge density, and (c) ion acoustic waves in the quarter critical density region for the laser pulse time
![]() $t_{p}=0$
and the simulation time
$t_{p}=0$
and the simulation time
![]() $t=5$
ps. Color bars are in logarithmic units.
$t=5$
ps. Color bars are in logarithmic units.

Figure 6. (a) Distribution of the Poynting vector (
![]() $x$
-component in W/cm
$x$
-component in W/cm
![]() $^{2}$
) in real space around quarter critical density, (b) the charge density
$^{2}$
) in real space around quarter critical density, (b) the charge density
![]() $(Zn_{i}-n_{e})/n_{c}$
and (c) the ion density normalized to the critical density
$(Zn_{i}-n_{e})/n_{c}$
and (c) the ion density normalized to the critical density
![]() $Zn_{i}/n_{c}$
for the laser pulse time
$Zn_{i}/n_{c}$
for the laser pulse time
![]() $t_{p}=0$
and the simulation time
$t_{p}=0$
and the simulation time
![]() $t=5$
ps. The solid black lines represent the density range between
$t=5$
ps. The solid black lines represent the density range between
![]() $0.22n_{c}$
and
$0.22n_{c}$
and
![]() $0.28n_{c}$
on the initial density profile.
$0.28n_{c}$
on the initial density profile.
4.1 Laser–plasma interaction near the quarter critical density
The quarter critical density is identified in Figure 2 as the major domain of laser absorption and the major origin of hot electrons. Figure 5 shows the Fourier spectra of the magnetic field (electromagnetic waves), charge density perturbations, and ion density perturbations in the density range near the quarter critical density, corresponding to a spatial width of
![]() $50\unicode[STIX]{x1D706}_{0}$
in the laser propagation direction. These are instantaneous spectra which resolve only the absolute values of the corresponding wavenumber components. Therefore, only a quarter of the phase space is shown.
$50\unicode[STIX]{x1D706}_{0}$
in the laser propagation direction. These are instantaneous spectra which resolve only the absolute values of the corresponding wavenumber components. Therefore, only a quarter of the phase space is shown.
One can see the harmonics of the laser frequency and the central structure at
![]() $|k_{y}|\lesssim 0.2k_{0}$
in addition to the main laser field at
$|k_{y}|\lesssim 0.2k_{0}$
in addition to the main laser field at
![]() $k\simeq 0.85k_{0}$
in the spectrum of the electromagnetic field in Figure 5(a). The wavelength shift of the main field is due to the dispersion of electromagnetic waves in plasma,
$k\simeq 0.85k_{0}$
in the spectrum of the electromagnetic field in Figure 5(a). The wavelength shift of the main field is due to the dispersion of electromagnetic waves in plasma,
![]() $k=k_{0}\sqrt{1-n_{e}/n_{c}}$
, and the broad angular distribution can be explained by the contribution of SBS daughter waves. This can be clearly seen in the intensity distribution in real space, shown in Figure 6(a): the laser beam is strongly filamented, and backward propagating electromagnetic waves are localized inside the filaments. In our conditions of a high laser intensity, the filamentation instability proceeds in a strongly coupled regime and has the highest growth rate,
$k=k_{0}\sqrt{1-n_{e}/n_{c}}$
, and the broad angular distribution can be explained by the contribution of SBS daughter waves. This can be clearly seen in the intensity distribution in real space, shown in Figure 6(a): the laser beam is strongly filamented, and backward propagating electromagnetic waves are localized inside the filaments. In our conditions of a high laser intensity, the filamentation instability proceeds in a strongly coupled regime and has the highest growth rate,
![]() $\unicode[STIX]{x1D6FE}_{\text{fil}}\simeq \unicode[STIX]{x1D714}_{pi}a_{0}/\sqrt{2}$
[Reference Langdon and Lasinski16], where
$\unicode[STIX]{x1D6FE}_{\text{fil}}\simeq \unicode[STIX]{x1D714}_{pi}a_{0}/\sqrt{2}$
[Reference Langdon and Lasinski16], where
![]() $\unicode[STIX]{x1D714}_{pi}=(Z_{i}^{2}e^{2}n_{i}/\unicode[STIX]{x1D716}_{0}m_{i})^{1/2}$
is the ion plasma frequency. The period of spatial modulation of the laser intensity of
$\unicode[STIX]{x1D714}_{pi}=(Z_{i}^{2}e^{2}n_{i}/\unicode[STIX]{x1D716}_{0}m_{i})^{1/2}$
is the ion plasma frequency. The period of spatial modulation of the laser intensity of
![]() $5\unicode[STIX]{x1D706}_{0}{-}8\unicode[STIX]{x1D706}_{0}$
can be seen in Figure 6(a). Longitudinal modulation of laser filaments with a period
$5\unicode[STIX]{x1D706}_{0}{-}8\unicode[STIX]{x1D706}_{0}$
can be seen in Figure 6(a). Longitudinal modulation of laser filaments with a period
![]() ${\sim}0.55\unicode[STIX]{x1D706}_{0}$
observed in Figure 6(a) is due to the interference of the incident laser field with the backward propagating SBS waves. The intensity of the laser wave in the filaments is increased by a factor of 10 compared to the incident laser intensity, thus providing a strong boost for the scattering instabilities, SBS and SRS, which can be identified in the Fourier spectra of the electron and ion acoustic plasma waves.
${\sim}0.55\unicode[STIX]{x1D706}_{0}$
observed in Figure 6(a) is due to the interference of the incident laser field with the backward propagating SBS waves. The intensity of the laser wave in the filaments is increased by a factor of 10 compared to the incident laser intensity, thus providing a strong boost for the scattering instabilities, SBS and SRS, which can be identified in the Fourier spectra of the electron and ion acoustic plasma waves.
The structure of the Fourier spectrum of the charge density perturbation in Figure 5(b) aligned in the laser propagation direction contains four particular features: plasma waves with
![]() $k_{x}\simeq 0.9k_{0}$
, a central circular structure with
$k_{x}\simeq 0.9k_{0}$
, a central circular structure with
![]() $k\simeq 0.4k_{0}$
, an intense structure at
$k\simeq 0.4k_{0}$
, an intense structure at
![]() $k_{x}\simeq 1.8k_{0}$
, and its harmonic at
$k_{x}\simeq 1.8k_{0}$
, and its harmonic at
![]() $k_{x}\simeq 3.6k_{0}$
. The structure at
$k_{x}\simeq 3.6k_{0}$
. The structure at
![]() $1.8k_{0}$
is a quasistatic electron density perturbation driven by interference of the laser and SBS waves in the filaments. It corresponds to the longitudinal modulation of filaments with a period
$1.8k_{0}$
is a quasistatic electron density perturbation driven by interference of the laser and SBS waves in the filaments. It corresponds to the longitudinal modulation of filaments with a period
![]() ${\sim}0.55\unicode[STIX]{x1D706}_{0}$
observed in Figure 6(a), to the similar modulation of the charge and density seen in Figures 6(b) and 6(c), and to the feature at
${\sim}0.55\unicode[STIX]{x1D706}_{0}$
observed in Figure 6(a), to the similar modulation of the charge and density seen in Figures 6(b) and 6(c), and to the feature at
![]() $k_{x}\simeq 1.8k_{0}$
in the Fourier spectrum of the ion density in Figure 5(c). The latter represents also the SBS-driven ion acoustic waves. These charge and density modulations are strong, with a relative amplitude of the order of 20%–30%. Consequently, they produce a second harmonic at
$k_{x}\simeq 1.8k_{0}$
in the Fourier spectrum of the ion density in Figure 5(c). The latter represents also the SBS-driven ion acoustic waves. These charge and density modulations are strong, with a relative amplitude of the order of 20%–30%. Consequently, they produce a second harmonic at
![]() $k_{x}\simeq 3.6k_{0}$
, also seen in Figures 5(b) and 5(c). The amplitude of the electrostatic field can be evaluated from Figure 6(b). The amplitude of the charge fluctuations
$k_{x}\simeq 3.6k_{0}$
, also seen in Figures 5(b) and 5(c). The amplitude of the electrostatic field can be evaluated from Figure 6(b). The amplitude of the charge fluctuations
![]() $(Zn_{i}-n_{e})/n_{c}\sim 0.1$
with wavenumber
$(Zn_{i}-n_{e})/n_{c}\sim 0.1$
with wavenumber
![]() $k_{x}\simeq 1.8k_{0}$
corresponds to an electrostatic field
$k_{x}\simeq 1.8k_{0}$
corresponds to an electrostatic field
![]() $E\sim 0.05E_{c}$
, where
$E\sim 0.05E_{c}$
, where
![]() $E_{c}=m_{e}\unicode[STIX]{x1D714}_{0}c/e$
is the Compton field, comparable to the incident laser field with the dimensionless amplitude
$E_{c}=m_{e}\unicode[STIX]{x1D714}_{0}c/e$
is the Compton field, comparable to the incident laser field with the dimensionless amplitude
![]() $a_{0}=E_{\text{las}}/E_{c}\simeq 0.1$
.
$a_{0}=E_{\text{las}}/E_{c}\simeq 0.1$
.

Figure 7. (a) Spatial distribution of the Poynting vector (
![]() $x$
-component in
$x$
-component in
![]() $\text{W}/\text{cm}^{2}$
) in real space around the critical density, (b) the charge density
$\text{W}/\text{cm}^{2}$
) in real space around the critical density, (b) the charge density
![]() $(Zn_{i}-n_{e})/n_{c}$
and (c) the ion density normalized to the critical density
$(Zn_{i}-n_{e})/n_{c}$
and (c) the ion density normalized to the critical density
![]() $Zn_{i}/n_{c}$
for the laser pulse time
$Zn_{i}/n_{c}$
for the laser pulse time
![]() $t_{p}=0$
and the simulation time
$t_{p}=0$
and the simulation time
![]() $t=5$
ps. The solid black lines represent the region
$t=5$
ps. The solid black lines represent the region
![]() $(0.9-1)n_{c}$
near the critical density.
$(0.9-1)n_{c}$
near the critical density.
The peak in the charge density fluctuations at
![]() $k_{x}\simeq 0.9k_{0}$
corresponds to the wavenumber of the laser field near quarter critical density. It represents the SRS-driven plasma waves. The direction of propagation of the SRS daughter electromagnetic waves can be deduced from Figure 5(a). They are represented by a feature in the domain
$k_{x}\simeq 0.9k_{0}$
corresponds to the wavenumber of the laser field near quarter critical density. It represents the SRS-driven plasma waves. The direction of propagation of the SRS daughter electromagnetic waves can be deduced from Figure 5(a). They are represented by a feature in the domain
![]() $k\ll k_{0}$
extended in the transverse direction with
$k\ll k_{0}$
extended in the transverse direction with
![]() $k_{y}\lesssim 0.3k_{0}$
. This is a clear indication of the SRS sidescattering, which is an absolute instability in this density range. By comparing the electric charge and ion density spatial distributions in panels (b) and (c) in Figure 6, we conclude that the plasma wave activity is localized in the region
$k_{y}\lesssim 0.3k_{0}$
. This is a clear indication of the SRS sidescattering, which is an absolute instability in this density range. By comparing the electric charge and ion density spatial distributions in panels (b) and (c) in Figure 6, we conclude that the plasma wave activity is localized in the region
![]() $x=230\unicode[STIX]{x1D706}_{0}{-}260\unicode[STIX]{x1D706}_{0}$
where the plasma density is close to or slightly below the quarter critical density. It coincides exactly with the zone of hot electron production seen in Figure 2.
$x=230\unicode[STIX]{x1D706}_{0}{-}260\unicode[STIX]{x1D706}_{0}$
where the plasma density is close to or slightly below the quarter critical density. It coincides exactly with the zone of hot electron production seen in Figure 2.
The obliquely propagating SRS daughter waves cannot easily escape the plasma because of their small wavenumber and large amplitude density fluctuations. They are strongly coupled to electron plasma waves and drive a secondary parametric decay instability (PDI) which corresponds to excitation of pairs of electron plasma and ion acoustic waves with equal and oppositely directed wavevectors. They are represented by a peak in the charge density fluctuations at
![]() $k\lesssim 0.4k_{0}$
in Figure 5(b). A similar signature can be seen in the spectrum of ion acoustic waves in Figure 5(c), although laser filamentation also contributes to this spectral feature. All these observations indicate SRS as the primary source of large-amplitude plasma waves, which undergo secondary decays and efficiently accelerate electrons. The dominant role of SRS in laser energy absorption is confirmed by the fact that the phase velocity of the principal plasma wave
$k\lesssim 0.4k_{0}$
in Figure 5(b). A similar signature can be seen in the spectrum of ion acoustic waves in Figure 5(c), although laser filamentation also contributes to this spectral feature. All these observations indicate SRS as the primary source of large-amplitude plasma waves, which undergo secondary decays and efficiently accelerate electrons. The dominant role of SRS in laser energy absorption is confirmed by the fact that the phase velocity of the principal plasma wave
![]() $v_{\text{ph}}=(\unicode[STIX]{x1D714}_{0}/2)/(0.9k_{0})\simeq 0.55c$
corresponds to an electron energy of 100 keV and is very close to the effective temperature of hot electrons given in Table 2. Other processes, including particle trapping and quasi-linear-like diffusion, may also accelerate electrons, which requires further more detailed investigations.
$v_{\text{ph}}=(\unicode[STIX]{x1D714}_{0}/2)/(0.9k_{0})\simeq 0.55c$
corresponds to an electron energy of 100 keV and is very close to the effective temperature of hot electrons given in Table 2. Other processes, including particle trapping and quasi-linear-like diffusion, may also accelerate electrons, which requires further more detailed investigations.
Manifestations of this process can be also seen in the low-frequency patterns in Figure 5. In the Fourier spectrum in panel (a) it is represented by the feature at
![]() $k_{x}\simeq (0.3{-}0.6)k_{0}$
. In the frequency spectrum of backscattered waves in panel (b) it is shown as a low-frequency lobe extending below
$k_{x}\simeq (0.3{-}0.6)k_{0}$
. In the frequency spectrum of backscattered waves in panel (b) it is shown as a low-frequency lobe extending below
![]() $\frac{1}{2}\unicode[STIX]{x1D714}_{0}$
. Such very low frequency electromagnetic waves cannot be directly produced in SRS. They are related to the electron plasma waves produced by secondary parametric instabilities and transformed in electromagnetic waves on steep plasma density gradients on the edges of filaments.
$\frac{1}{2}\unicode[STIX]{x1D714}_{0}$
. Such very low frequency electromagnetic waves cannot be directly produced in SRS. They are related to the electron plasma waves produced by secondary parametric instabilities and transformed in electromagnetic waves on steep plasma density gradients on the edges of filaments.
4.2 Laser–plasma interaction near the critical density
The processes near the critical density can be also understood from comparison of the spatial distribution of waves and the analysis of their Fourier spectra. The spatial distribution of the wave activity is shown in Figure 7. The average plasma density increases from
![]() $0.55n_{c}$
to
$0.55n_{c}$
to
![]() $n_{c}$
over
$n_{c}$
over
![]() $30\unicode[STIX]{x1D706}_{0}$
, and then remains flat beyond
$30\unicode[STIX]{x1D706}_{0}$
, and then remains flat beyond
![]() $x=320\unicode[STIX]{x1D706}_{0}$
. Vertical dashed lines identify the zone with an average density higher than
$x=320\unicode[STIX]{x1D706}_{0}$
. Vertical dashed lines identify the zone with an average density higher than
![]() $0.9n_{c}$
and where the density plateau begins. The electromagnetic field distribution in Figure 7(a) shows strong filamentation of the laser light with a period of a few wavelengths in the plasma with a density
$0.9n_{c}$
and where the density plateau begins. The electromagnetic field distribution in Figure 7(a) shows strong filamentation of the laser light with a period of a few wavelengths in the plasma with a density
![]() $n_{e}<0.9n_{c}$
. The interference structure with a period
$n_{e}<0.9n_{c}$
. The interference structure with a period
![]() ${\sim}\unicode[STIX]{x1D706}_{0}$
within each filament corresponds to beating of the incident laser and reflected SBS waves. (Because of dispersion, the laser wavelength at this density is
${\sim}\unicode[STIX]{x1D706}_{0}$
within each filament corresponds to beating of the incident laser and reflected SBS waves. (Because of dispersion, the laser wavelength at this density is
![]() ${\sim}2\unicode[STIX]{x1D706}_{0}$
.) However, the laser intensity in this region is strongly reduced: it is on average 4–5 times smaller than the incident intensity.
${\sim}2\unicode[STIX]{x1D706}_{0}$
.) However, the laser intensity in this region is strongly reduced: it is on average 4–5 times smaller than the incident intensity.
One can also see weak small-scale periodic structures
![]() ${\sim}0.55\unicode[STIX]{x1D706}_{0}$
indicating the sites of the second-harmonic generation. They appear between the filaments, where the plasma density is higher than the critical density. This density interval is also marked by strong-amplitude plasma waves localized in a narrow spatial region near density
${\sim}0.55\unicode[STIX]{x1D706}_{0}$
indicating the sites of the second-harmonic generation. They appear between the filaments, where the plasma density is higher than the critical density. This density interval is also marked by strong-amplitude plasma waves localized in a narrow spatial region near density
![]() $0.9n_{c}$
in Figure 7(b). A correlation between excitation of the second harmonic of the laser field and plasma waves indicates the process of resonance absorption. This hypothesis is confirmed also by the spectrum of charge density fluctuations in Figure 8(b) showing a broad lobe with wavenumbers extending between
$0.9n_{c}$
in Figure 7(b). A correlation between excitation of the second harmonic of the laser field and plasma waves indicates the process of resonance absorption. This hypothesis is confirmed also by the spectrum of charge density fluctuations in Figure 8(b) showing a broad lobe with wavenumbers extending between
![]() $1.5k_{0}$
and
$1.5k_{0}$
and
![]() $2.5k_{0}$
. Such a broad spectrum is explained by a large amplitude of plasma waves
$2.5k_{0}$
. Such a broad spectrum is explained by a large amplitude of plasma waves
![]() $E/E_{c}\sim 0.1$
generating secondary parametric decay of the plasma waves (PDI). In panels (b) and (c) in Figure 8, in the same spatial region, one can see the electron and ion acoustic plasma waves propagating in the transverse direction. These are the products of the PDI driven by the laser wave near its turning point.
$E/E_{c}\sim 0.1$
generating secondary parametric decay of the plasma waves (PDI). In panels (b) and (c) in Figure 8, in the same spatial region, one can see the electron and ion acoustic plasma waves propagating in the transverse direction. These are the products of the PDI driven by the laser wave near its turning point.
Laser penetration into the dense plasma terminates with the formation of cavities seen at
![]() $x\sim 317\unicode[STIX]{x1D706}_{0}$
in Figure 7(c). Formation of such cavities or “bubbles” was reported already in early publications on the laser absorption and parametric processes in near-critical plasmas[Reference Estabrook, Valeo and Kruer6, Reference Langdon and Lasinski16–Reference Riconda and Weber18], but because of much shorter spatial scales the role of laser filamentation and the parametric processes near the quarter critical plasma was overlooked.
$x\sim 317\unicode[STIX]{x1D706}_{0}$
in Figure 7(c). Formation of such cavities or “bubbles” was reported already in early publications on the laser absorption and parametric processes in near-critical plasmas[Reference Estabrook, Valeo and Kruer6, Reference Langdon and Lasinski16–Reference Riconda and Weber18], but because of much shorter spatial scales the role of laser filamentation and the parametric processes near the quarter critical plasma was overlooked.

Figure 8. Fourier spectra of (a) electromagnetic waves, (b) electron plasma waves – charge density, and (c) ion acoustic waves in the region around critical density for the laser pulse time
![]() $t_{p}=0$
and the simulation time
$t_{p}=0$
and the simulation time
![]() $t=5$
ps. Color bars are in logarithmic units.
$t=5$
ps. Color bars are in logarithmic units.
The structures shown in Figure 7 in real space are also observed in the Fourier spectra shown in Figure 8. The spectrum of electromagnetic waves in Figure 8(a) consists of an intensity circle with
![]() $k\simeq 1.8k_{0}$
, representing second-harmonic radiation, and a very intense and broad feature at
$k\simeq 1.8k_{0}$
, representing second-harmonic radiation, and a very intense and broad feature at
![]() $k\simeq 0.5k_{0}$
, representing the Brillouin scattered light. SBS and filamentation manifest themselves in the Fourier spectra of ion density in Figure 8(c), with two features at
$k\simeq 0.5k_{0}$
, representing the Brillouin scattered light. SBS and filamentation manifest themselves in the Fourier spectra of ion density in Figure 8(c), with two features at
![]() $k_{x}\simeq (1-2)k_{0}$
and
$k_{x}\simeq (1-2)k_{0}$
and
![]() $\unicode[STIX]{x0394}k_{y}\sim 0.2k_{0}$
, respectively. The relatively small ion acoustic wavenumber for the backscattered SBS is explained by electromagnetic wave dispersion.
$\unicode[STIX]{x0394}k_{y}\sim 0.2k_{0}$
, respectively. The relatively small ion acoustic wavenumber for the backscattered SBS is explained by electromagnetic wave dispersion.
The process of linear transformation of electromagnetic waves into longitudinal plasma waves of the same frequency is therefore the dominant laser absorption process near the critical density, but its contribution is apparently much smaller compared to the processes near the quarter critical density. The wavenumbers of resonantly excited plasma waves correspond to phase velocities
![]() $0.3c{-}0.5c$
, and therefore they generate electrons with energies in the range 10–70 keV, which are smaller than the effective hot electron temperature shown in Figure 2(a) and Table 2 for this case. On the other hand, in the simulations at the laser pulse time
$0.3c{-}0.5c$
, and therefore they generate electrons with energies in the range 10–70 keV, which are smaller than the effective hot electron temperature shown in Figure 2(a) and Table 2 for this case. On the other hand, in the simulations at the laser pulse time
![]() $t_{p}=-200$
,
$t_{p}=-200$
,
![]() $-100$
or 200 ps, the absorption around critical density is more significant, and thus the hot electron temperature is effectively lower.
$-100$
or 200 ps, the absorption around critical density is more significant, and thus the hot electron temperature is effectively lower.
5 Discussion
The laser–plasma interaction features discussed in detail in the previous sections can be summarized as follows. The pulse entering the plasma undergoes strong filamentation, resulting in narrow density channels transporting laser energy with an intensity enhanced up to 10 times the initial laser intensity. This intensity enhancement could be even stronger in the realistic 3D case, where filamentation proceeds in two transverse directions. Concentration of the laser flux in the filaments accompanied by amplification of the laser electric field drives strong scattering instabilities, SBS and SRS. The former is responsible for the major part of the scattered light emitted in a wide cone with an opening angle
![]() $20^{\circ }{-}30^{\circ }$
. Approximately half of the scattered energy goes into the solid angle of the focusing optics. The zone of strong SBS is localized in the density range
$20^{\circ }{-}30^{\circ }$
. Approximately half of the scattered energy goes into the solid angle of the focusing optics. The zone of strong SBS is localized in the density range
![]() $(0.2{-}0.5)n_{c}$
, so a significant part of the laser energy has access to a density close to the quarter critical density where absolute SRS develops. It results in the excitation of large-amplitude plasma waves and efficient electron acceleration. SRS can account for absorption up to 20%–25% of the incident laser energy, and produce electrons with an exponential energy distribution and temperature of 80–90 keV. These electrons contribute about half the energy flux entering from the corona into the overdense plasma.
$(0.2{-}0.5)n_{c}$
, so a significant part of the laser energy has access to a density close to the quarter critical density where absolute SRS develops. It results in the excitation of large-amplitude plasma waves and efficient electron acceleration. SRS can account for absorption up to 20%–25% of the incident laser energy, and produce electrons with an exponential energy distribution and temperature of 80–90 keV. These electrons contribute about half the energy flux entering from the corona into the overdense plasma.
Only a small fraction of the daughter SRS waves leave the plasma. They undergo a secondary parametric decay instability and scattering on large-amplitude plasma waves, so the energy flux carried with downscattered electromagnetic waves in the backward direction is 4–5 times smaller than the electron energy flux. Moreover, the inverse process of resonance transformation of electron plasma waves into electromagnetic waves on small-scale density fluctuations results in broadening of the reflected light spectrum to frequencies below half of the laser frequency. Analysis of the spectrum of reflected light in that long-wavelength domain may provide important information on processes near the quarter critical density and confirm the present scenario of laser–plasma interaction.
The plasma zone close to the critical density also shows a similar ensemble of nonlinear processes, including small-scale filamentation, SBS in the filaments, resonance transformation of laser light in plasma waves on a steepened density profile, and secondary instabilities of laser and plasma waves and PDI, resulting in laser energy absorption, electron acceleration and heating. However, the fraction of the laser energy penetrating to the critical density region is less significant, and its contribution to the total laser energy absorption is relatively small. Moreover, the phase velocity of plasma waves excited in that zone is lower, and the energy of accelerated electrons is 2–3 times lower than in the quarter critical density.
These processes analyzed in detail for the time corresponding to the laser pulse maximum have also been observed in simulations corresponding to other laser times and intensities. However, the relative role of the processes near the critical and quarter critical densities changes. The laser filamentation is less strong, resulting in a smaller SRS, and favoring excitation of two-plasmon decay (TPD), which is completely suppressed at high laser intensities. Consequently a smaller fraction of the laser energy is absorbed near the quarter critical density, and the resonance laser absorption near the critical density makes a larger contribution with electrons accelerated to smaller energies.
The described scenario of laser–plasma interaction corresponds to the particular conditions of a long-wavelength, high-intensity laser pulse. While applying this scenario to realistic conditions one would need to account for collisional processes, which will result in an increase of the total absorbed laser energy. However, as the collisional processes operate near the critical density, the processes near the quarter critical density will remain unchanged. Measurements of the spectrum of backscattered laser light and the hot electron energy flux in the overdense plasma are needed for experimental verification of the proposed scenario.
Acknowledgements
This work has been carried out within the framework of the EUROfusion Consortium and has received funding from the Euratom Research and Training Programme 2014–2018 under grant agreement No. 633053. The views and opinions expressed herein do not necessarily reflect those of the European Commission. This work was supported by the project ELITAS (CZ.02.1.01/0.0/0.0/16_013/0001793) and by the project High Field Initiative (CZ.02.1.01/0.0/0.0/15_003/0000449), both from the European Regional Development Fund. It is also supported by the project ADONIS (Advanced research using high intensity laser produced photons and particles), CZ.02.1.01/0.0/0.0/16_019/0000789, from the European Regional Development Fund. This work was partially supported by the Center of Advanced Applied Natural Sciences, Reg. No. CZ.02.1.01/0.0/0.0/16_019/0000778, and by the Operational Program Research, Development and Education, co-financed by the European Structural and Investment Funds and the state budget of the Czech Republic.