1 Introduction
Temperature is one of the most important parameters for characterizing the thermodynamic state of matter. Temperature measurements of materials under extreme conditions play an important role in military applications, inertial confinement fusion[Reference Drake1], high-energy-density physics[Reference Hicks, Boehly, Eggert, Miller, Celliers and Collins2, Reference Zeldovich and Raizer3], and fundamental material studies[Reference Asay, Shahinpoor and Davison4]. For instance, the establishment of the theoretical equation of state (EOS) model at ultra-high pressures is very sensitive to the temperature. Shock temperature measurements are among the important means to examine and test the theoretical EOS model under extreme conditions. High-power lasers have been increasingly used as drivers for shock-wave experiments, and can produce extremely high pressures[Reference Miller, Boehly, Melchior, Meyerhofer, Celliers, Eggert, Hicks, Sorce, Oertel and Emmel5–Reference He, Shu, Huang, Zhang, Jia, Zhang, Tu, Wang, Ye, Xie, Fang, Pei and Fu11].
To date, measurements of the mechanical parameters, such as the shock-wave velocity and pressure, of a system have reached a relatively mature state in shock-wave experiments to study the EOS. However, accurately measuring thermodynamic parameters, such as the temperature, remains a difficult task because of the measurement complexity, precision requirements for the instruments, and the establishment of the calculation model[Reference Zeldovich and Raizer3]. To date, the optical radiation method has been widely used for transient measurements of the shock temperature. The shock temperature of materials can be inferred from the recorded self-emission of the shocked materials by comparing the emission to a calibrated Planckian radiator. A streaked optical pyrometer (SOP) is commonly used to measure the self-emission[Reference Miller, Boehly, Melchior, Meyerhofer, Celliers, Eggert, Hicks, Sorce, Oertel and Emmel5, Reference Lyzenga and Ahrens12–Reference Gregor, Boni, Sorce, Kendrick, Mccoy, Polsin, Boehly, Celliers, Collins and Fratanduono16].
Although the SOP system has been widely adopted in shock temperature measurements, the reliability of this system has always been questioned. Firstly, the method of temperature measurement based on Planck’s theory has been proposed for decades, but few people have validated the SOP system with more than one standard source to prove its reliability. Secondly, Zeldovich and Raizer[Reference Zeldovich and Raizer3] and Tan[Reference Hua17] have presented different physical understandings of emissivity. The former held that emissivity is a function of frequency, while the latter considered that emissivity is independent of frequency and the measured surface temperature is the composition of the temperature behind the shock front. Thirdly, some researchers have proposed that the problem of surface radiation and absorption is complicated and difficult to explain[Reference Higginson, Mcnaney, Swift, Bartal, Hey, Kodama, Pape, Le Mackinnon, Mariscal and Nakamura18, Reference Fernandez, Barnes, Mocko and Zavorka19]. Effective verification and assessment of the reliability of the diagnostic method is a common difficulty. Therefore, it is necessary to develop methods to calibrate and verify the diagnostic method and assess the reliability of the SOP system. This ensures the validity and rationality of the obtained shock temperature data and addresses concerns regarding the feasibility of the SOP system applied to high-temperature measurements.
Here, we present a method to calibrate and verify the SOP system using two kinds of Planckian radiator standard lamp sources with different color temperatures to calibrate the system. The two lamps are regarded as the standard for each other in the SOP system. The relative deviation between the measured data and the standard value was calibrated for, enabling the SOP system to be used at thousands of kelvin. In addition, a method to analyze the uncertainty and sensitivity of the SOP system is described. A series of laser-induced shock experiments were conducted at a laser facility to verify the reliability of the SOP system for temperature measurements at tens of thousands of kelvin.
2 Verification of the SOP system
2.1 Theoretical basis
The temperature measurement diagnostic system is based on Planck’s black-body theory, which states that all bodies of finite temperature emit with a spectral radiance characteristic of their thermal state[Reference Lyzenga and Ahrens12]. For standard lamp and shock temperature experiments that can be regarded as a gray body, we relate the temperature
![]() $T$
to the spectral radiance
$T$
to the spectral radiance
![]() $L(\unicode[STIX]{x1D706})$
by Planck’s law:
$L(\unicode[STIX]{x1D706})$
by Planck’s law:
where
![]() $h$
is Planck’s constant,
$h$
is Planck’s constant,
![]() $c$
is the speed of light,
$c$
is the speed of light,
![]() $k$
is the Boltzmann constant,
$k$
is the Boltzmann constant,
![]() $\unicode[STIX]{x1D706}$
is the wavelength of the SOP channel, and
$\unicode[STIX]{x1D706}$
is the wavelength of the SOP channel, and
![]() $T$
is the temperature of the body. The standard lamps are specially designed so that the emissivity
$T$
is the temperature of the body. The standard lamps are specially designed so that the emissivity
![]() $\unicode[STIX]{x1D700}$
has a weak correlation with the wavelength in our calibrations.
$\unicode[STIX]{x1D700}$
has a weak correlation with the wavelength in our calibrations.
Two calibrated, Planckian radiator, standard lamps with different color temperatures were used in the calibration and verification of the SOP system, and are regarded as the known standard and unknown source for each other. One of the lamps is a CSTM-USLR-S12F produced by American Labsphere Incorporated, a National Institute of Standards and Technology (NIST)-traceable halogen tungsten lamp
![]() $(T\sim 3000~\text{K})$
of known spectral radiance accurate to
$(T\sim 3000~\text{K})$
of known spectral radiance accurate to
![]() ${\sim}1\%$
, with an emissivity of
${\sim}1\%$
, with an emissivity of
![]() $(6\pm 0.04)\times 10^{-3}$
. The uniformity of the lamp emissivity is better than 98% according to the original calibration report. The other lamp has a customized filter placed in front of the outlet of a standard halogen tungsten lamp (CSTM-USLR-S12F), also a specially designed NIST-traceable Planckian radiator with a higher color temperature
$(6\pm 0.04)\times 10^{-3}$
. The uniformity of the lamp emissivity is better than 98% according to the original calibration report. The other lamp has a customized filter placed in front of the outlet of a standard halogen tungsten lamp (CSTM-USLR-S12F), also a specially designed NIST-traceable Planckian radiator with a higher color temperature
![]() $(T\sim 5000~\text{K})$
. The filter completely covers the outlet and is spatially uniform, with a multilayer dielectric film structure to make the lamp consistent with the theoretical Planck curve at
$(T\sim 5000~\text{K})$
. The filter completely covers the outlet and is spatially uniform, with a multilayer dielectric film structure to make the lamp consistent with the theoretical Planck curve at
![]() ${\sim}5000~\text{K}$
in the visible range (380–740 nm). The measured color temperature and emissivity of this lamp are
${\sim}5000~\text{K}$
in the visible range (380–740 nm). The measured color temperature and emissivity of this lamp are
![]() $(4956\pm 10)~\text{K}$
and
$(4956\pm 10)~\text{K}$
and
![]() $(2.5\pm 0.03)\times 10^{-4}$
, respectively, according to the original test report. The deviation between the measured spectral radiance and the theoretical Planck curve is designed to be lower than 10% in the visible range. The spectral radiance and the Planck fit of both lamps are shown in Figure 1.
$(2.5\pm 0.03)\times 10^{-4}$
, respectively, according to the original test report. The deviation between the measured spectral radiance and the theoretical Planck curve is designed to be lower than 10% in the visible range. The spectral radiance and the Planck fit of both lamps are shown in Figure 1.

Figure 1. Spectral radiance and Planck fit of the lower-color-temperature
![]() $({\sim}3000~\text{K})$
halogen tungsten lamp (thick orange line and thin red line) and the higher-color-temperature
$({\sim}3000~\text{K})$
halogen tungsten lamp (thick orange line and thin red line) and the higher-color-temperature
![]() $({\sim}5000~\text{K})$
specially designed lamp (thick blue line and thin purple line).
$({\sim}5000~\text{K})$
specially designed lamp (thick blue line and thin purple line).
2.2 Experimental configuration
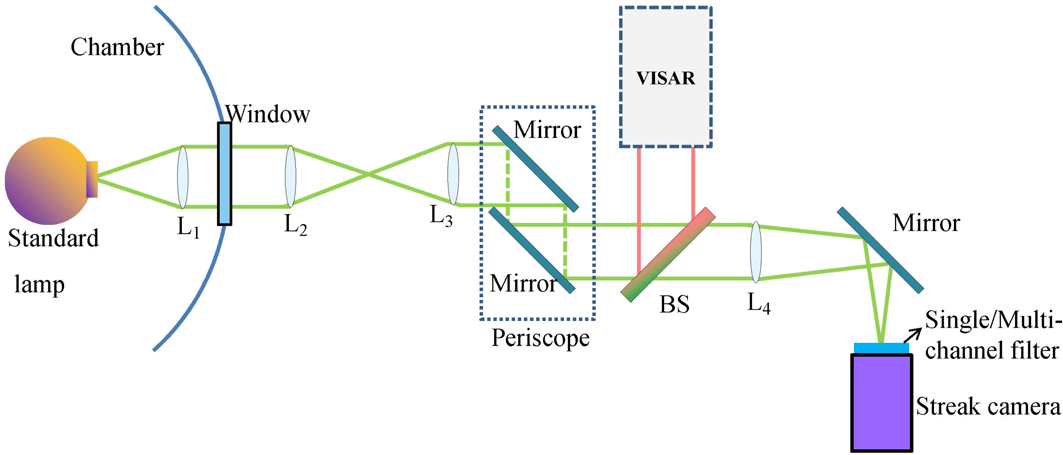
Calibration experiments were conducted at the ‘Shenguang-II’ laser facility platform. The optical path of the calibration is identical to the laser-induced shock experiments. Figure 2 shows a schematic of the calibration and verification configuration of the SOP system. A velocity interferometry system for any reflector (VISAR) is combined with the SOP system on the platform to permit simultaneous velocity and temperature measurements. The SOP system projects the emission from the standard lamp to a streak camera. An SC-10 streak camera produced by Optronis Company was used in our calibrations and experiments. The streak camera incorporates a streak tube with an S20 photocathode, a high-voltage power supply and control electronics. The dynamic sweep range of the camera is adjustable from 200 ps to 100 ms. The full-width at half-maximum (FWHM) of the line spread function (LSF) and the spectral response of the streak camera can be seen in Figures 3(a) and 3(b), respectively. The streak camera slit width used in our calibrations and experiments was
![]() $200~\unicode[STIX]{x03BC}\text{m}$
.
$200~\unicode[STIX]{x03BC}\text{m}$
.

Figure 2. Calibration and verification configuration of the SOP system (top view).
The outlet of the standard lamp is placed at the object plane of the imaging system. The first part of the imaging system (L1) is composed of several achromatic lenses to produce a magnified real image. This real image is transmitted and collimated by the compound lenses (L2 and L3). After passing through the periscope system, the projection is imaged by L4 at the slit of the SOP streak camera. The specially designed beam splitter (BS) is a dichroic mirror that reflects the probe beam (660 nm) to the VISAR while transmitting the thermal emission to the SOP. A single-channel or multi-channel narrowband filter was placed in front of the slit of the streak camera to allow wavelength-specific light transmission.

Figure 3. (a) LSF FWHM and (b) spectral response of the SC-10 streak camera.
When starting the calibrations, the lower-color-temperature lamp (marked as Lamp A) was first placed on the object plane, as shown in Figure 2. Here, Lamp A is regarded as a known standard light source. Care was taken to ensure that the luminescent image of Lamp A was centered on the slit of the streak camera. A lens (L1) in the chamber was introduced to collect the emission for the same solid angle in different experiments and calibrations. After the light had passed through the SOP system, the emission was recorded on the streak camera during the luminous time. Calibrations were then carried out using microsecond sweeps[Reference Spaulding20]. The parameters related to the streak camera settings, such as the slits and micro-channel plate (MCP), must be the same in the calibrations to ensure consistency in the SOP transfer function. The streak camera was set to be in the dynamic mode, i.e., slow sweep mode, which is different from the static mode described by Miller et al. [Reference Miller, Boehly, Melchior, Meyerhofer, Celliers, Eggert, Hicks, Sorce, Oertel and Emmel5]. The camera output of a single pixel from the source is given by
![]() $C_{A}=t_{A}\unicode[STIX]{x1D702}_{A}\int _{\unicode[STIX]{x1D706}}L_{A}(\unicode[STIX]{x1D706})\unicode[STIX]{x1D711}_{A}(\unicode[STIX]{x1D706})\,\text{d}\unicode[STIX]{x1D706}$
, where
$C_{A}=t_{A}\unicode[STIX]{x1D702}_{A}\int _{\unicode[STIX]{x1D706}}L_{A}(\unicode[STIX]{x1D706})\unicode[STIX]{x1D711}_{A}(\unicode[STIX]{x1D706})\,\text{d}\unicode[STIX]{x1D706}$
, where
![]() $t$
is the effective luminous time;
$t$
is the effective luminous time;
![]() $\unicode[STIX]{x1D702}$
is the count related to the solid angle, luminous area, gain of the camera, and slit width;
$\unicode[STIX]{x1D702}$
is the count related to the solid angle, luminous area, gain of the camera, and slit width;
![]() $L(\unicode[STIX]{x1D706})$
is the spectral radiance; and
$L(\unicode[STIX]{x1D706})$
is the spectral radiance; and
![]() $\unicode[STIX]{x1D711}(\unicode[STIX]{x1D706})$
is the spectral response of the system. Next, the higher-color-temperature lamp (marked as Lamp B) was placed in the same position as Lamp A to ensure the same modulation transfer function between calibrations. Here, Lamp B is regarded as an unknown light source to be measured. The camera output of a single pixel from Lamp B is given by
$\unicode[STIX]{x1D711}(\unicode[STIX]{x1D706})$
is the spectral response of the system. Next, the higher-color-temperature lamp (marked as Lamp B) was placed in the same position as Lamp A to ensure the same modulation transfer function between calibrations. Here, Lamp B is regarded as an unknown light source to be measured. The camera output of a single pixel from Lamp B is given by
![]() $C_{B}=t_{B}\unicode[STIX]{x1D702}_{B}\int _{\unicode[STIX]{x1D706}}L_{B}(\unicode[STIX]{x1D706})\unicode[STIX]{x1D711}_{B}(\unicode[STIX]{x1D706})\,\text{d}\unicode[STIX]{x1D706}$
. Since the luminous modes of both lamps are similar and the slit width and camera gain were set to be the same in the calibrations, the relations
$C_{B}=t_{B}\unicode[STIX]{x1D702}_{B}\int _{\unicode[STIX]{x1D706}}L_{B}(\unicode[STIX]{x1D706})\unicode[STIX]{x1D711}_{B}(\unicode[STIX]{x1D706})\,\text{d}\unicode[STIX]{x1D706}$
. Since the luminous modes of both lamps are similar and the slit width and camera gain were set to be the same in the calibrations, the relations
![]() $\unicode[STIX]{x1D711}_{A}(\unicode[STIX]{x1D706})=\unicode[STIX]{x1D711}_{B}(\unicode[STIX]{x1D706})$
and
$\unicode[STIX]{x1D711}_{A}(\unicode[STIX]{x1D706})=\unicode[STIX]{x1D711}_{B}(\unicode[STIX]{x1D706})$
and
![]() $\unicode[STIX]{x1D702}_{A}=\unicode[STIX]{x1D702}_{B}$
could be obtained. By dividing
$\unicode[STIX]{x1D702}_{A}=\unicode[STIX]{x1D702}_{B}$
could be obtained. By dividing
![]() $C_{A}$
and
$C_{A}$
and
![]() $C_{B}$
, we can obtain a simple relationship between both lamps,
$C_{B}$
, we can obtain a simple relationship between both lamps,
![]() $L_{B}(\unicode[STIX]{x1D706})=L_{A}(\unicode[STIX]{x1D706})\cdot (t_{A}/t_{B})\cdot (C_{B}/C_{A})$
, assuming a small wavelength range of a single pixel[Reference He, Jia, Zhang, Luo, Huang, Shu, Fang, Ye, Xie, Xia and Fu10]. Since
$L_{B}(\unicode[STIX]{x1D706})=L_{A}(\unicode[STIX]{x1D706})\cdot (t_{A}/t_{B})\cdot (C_{B}/C_{A})$
, assuming a small wavelength range of a single pixel[Reference He, Jia, Zhang, Luo, Huang, Shu, Fang, Ye, Xie, Xia and Fu10]. Since
![]() $L_{A}(\unicode[STIX]{x1D706})$
is known and
$L_{A}(\unicode[STIX]{x1D706})$
is known and
![]() $t_{A}$
,
$t_{A}$
,
![]() $t_{B}$
,
$t_{B}$
,
![]() $C_{A}$
and
$C_{A}$
and
![]() $C_{B}$
can be obtained from the calibration experiments,
$C_{B}$
can be obtained from the calibration experiments,
![]() $L_{B}(\unicode[STIX]{x1D706})$
can be calculated directly. A single-channel or multi-channel narrowband filter was placed in front of the streak camera slit to determine the wavelength channel of the light transmission.
$L_{B}(\unicode[STIX]{x1D706})$
can be calculated directly. A single-channel or multi-channel narrowband filter was placed in front of the streak camera slit to determine the wavelength channel of the light transmission.

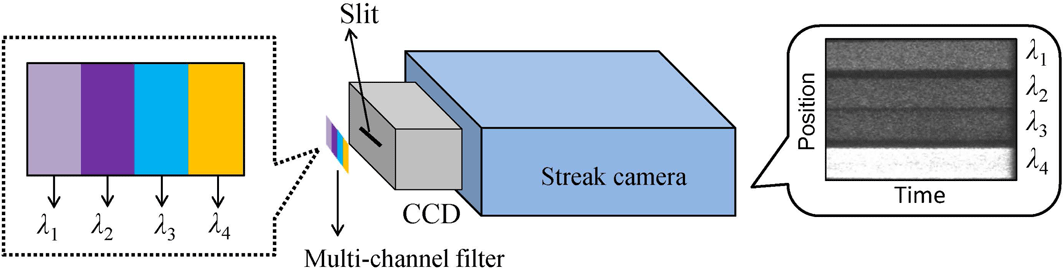
Figure 4. Schematic of the four-channel filter.
2.3 Multi-channel method
When the filter in front of the streak camera is a multi-channel filter, the temperature of Lamp B can be obtained by fitting several
![]() $L_{B}(\unicode[STIX]{x1D706})$
values at different wavelengths
$L_{B}(\unicode[STIX]{x1D706})$
values at different wavelengths
![]() $\unicode[STIX]{x1D706}$
[Reference Lyzenga and Ahrens12, Reference He, Zhou, Huang, Jia, Shu, Fang, Ye and Xie13]. Here, a four-channel narrowband filter was adopted in the SOP system. A schematic of the filter is shown in Figure 4. Four different narrowband channels were successively and uniformly coated on a thin rectangular filter for
$\unicode[STIX]{x1D706}$
[Reference Lyzenga and Ahrens12, Reference He, Zhou, Huang, Jia, Shu, Fang, Ye and Xie13]. Here, a four-channel narrowband filter was adopted in the SOP system. A schematic of the filter is shown in Figure 4. Four different narrowband channels were successively and uniformly coated on a thin rectangular filter for
![]() $\unicode[STIX]{x1D706}_{1}$
,
$\unicode[STIX]{x1D706}_{1}$
,
![]() $\unicode[STIX]{x1D706}_{2}$
,
$\unicode[STIX]{x1D706}_{2}$
,
![]() $\unicode[STIX]{x1D706}_{3}$
and
$\unicode[STIX]{x1D706}_{3}$
and
![]() $\unicode[STIX]{x1D706}_{4}$
, corresponding to 410, 450, 490 and 590 nm, respectively. The FWHM of each channel is less than 20 nm and the transmittance is greater than 80%. As for the spectrometer such as iHR550, there will be large intensity loss after grating splitting by the spectrometer. Thus, the intensity of light at a specific wavelength will be reduced to
$\unicode[STIX]{x1D706}_{4}$
, corresponding to 410, 450, 490 and 590 nm, respectively. The FWHM of each channel is less than 20 nm and the transmittance is greater than 80%. As for the spectrometer such as iHR550, there will be large intensity loss after grating splitting by the spectrometer. Thus, the intensity of light at a specific wavelength will be reduced to
![]() ${\sim}2\%$
of the original intensity. Therefore, the advantage of the multi-channel filter over a spectrometer is that the effective signal intensity is higher, making the signal-to-noise ratio better. The total width of the filter is the same as the horizontal width of the slit of the streak camera, while its height should be greater than that of the slit of the streak camera to cover the slit completely. Since the effective luminous time
${\sim}2\%$
of the original intensity. Therefore, the advantage of the multi-channel filter over a spectrometer is that the effective signal intensity is higher, making the signal-to-noise ratio better. The total width of the filter is the same as the horizontal width of the slit of the streak camera, while its height should be greater than that of the slit of the streak camera to cover the slit completely. Since the effective luminous time
![]() $t$
can be obtained from the streak camera,
$t$
can be obtained from the streak camera,
![]() $t=s_{w}/\text{pix}$
, where
$t=s_{w}/\text{pix}$
, where
![]() $s_{w}$
is the sweep time of the streak camera and pix is the number of pixels on the entire screen. Using the equation
$s_{w}$
is the sweep time of the streak camera and pix is the number of pixels on the entire screen. Using the equation
![]() $L_{B}(\unicode[STIX]{x1D706})=L_{A}(\unicode[STIX]{x1D706})\cdot (t_{A}/t_{B})\cdot (C_{B}/C_{A})$
, the spectral radiance of the lamp to be measured,
$L_{B}(\unicode[STIX]{x1D706})=L_{A}(\unicode[STIX]{x1D706})\cdot (t_{A}/t_{B})\cdot (C_{B}/C_{A})$
, the spectral radiance of the lamp to be measured,
![]() $L_{B}(\unicode[STIX]{x1D706})$
, can be obtained from the streak camera, and
$L_{B}(\unicode[STIX]{x1D706})$
, can be obtained from the streak camera, and
![]() $L_{A}(\unicode[STIX]{x1D706})$
can be found by integrating the spectrum of each channel. The values of
$L_{A}(\unicode[STIX]{x1D706})$
can be found by integrating the spectrum of each channel. The values of
![]() $t_{A}$
and
$t_{A}$
and
![]() $t_{B}$
are considered to be known. Given the calculated
$t_{B}$
are considered to be known. Given the calculated
![]() $L_{B}(\unicode[STIX]{x1D706})$
at different wavelengths, the emissivity and temperature can be simultaneously varied to obtain the best fit of the data using Equation (1), assuming that both parameters of Lamp B are unknown at this time. Here, the emissivity was considered as a constant or as linearly varying with wavelength. After fitting using the least squares method, values of
$L_{B}(\unicode[STIX]{x1D706})$
at different wavelengths, the emissivity and temperature can be simultaneously varied to obtain the best fit of the data using Equation (1), assuming that both parameters of Lamp B are unknown at this time. Here, the emissivity was considered as a constant or as linearly varying with wavelength. After fitting using the least squares method, values of
![]() $T_{B}=4893~\text{K}$
and
$T_{B}=4893~\text{K}$
and
![]() $\unicode[STIX]{x1D700}_{B}=2.2\times 10^{-4}$
were obtained, as shown in Figure 5(a). Since the original color temperature of Lamp B
$\unicode[STIX]{x1D700}_{B}=2.2\times 10^{-4}$
were obtained, as shown in Figure 5(a). Since the original color temperature of Lamp B
![]() $(T_{B0})$
was 4956 K according to the original production test report, the relative deviation between
$(T_{B0})$
was 4956 K according to the original production test report, the relative deviation between
![]() $T_{B0}$
and the measured
$T_{B0}$
and the measured
![]() $T_{B}$
, expressed as
$T_{B}$
, expressed as
![]() $\unicode[STIX]{x1D702}_{B}=|T_{B}-T_{B0}|/T_{B}=1.3\%$
was obtained. The error of the spectral radiance has been analyzed according to Equation (9) in Section 3. The streak camera counts of calibrations of both lamps and the spectral radiance of a known lamp all contribute to the uncertainty.
$\unicode[STIX]{x1D702}_{B}=|T_{B}-T_{B0}|/T_{B}=1.3\%$
was obtained. The error of the spectral radiance has been analyzed according to Equation (9) in Section 3. The streak camera counts of calibrations of both lamps and the spectral radiance of a known lamp all contribute to the uncertainty.
Similarly, Lamp B was considered as the standard lamp source and Lamp A as the source to be measured. Then, four calculated
![]() $L_{A}(\unicode[STIX]{x1D706})$
values are given at different wavelengths. After fitting using the least squares method, values of
$L_{A}(\unicode[STIX]{x1D706})$
values are given at different wavelengths. After fitting using the least squares method, values of
![]() $T_{A}=2904~\text{K}$
and
$T_{A}=2904~\text{K}$
and
![]() $\unicode[STIX]{x1D700}_{A}=0.007$
were obtained, as shown in Figure 5(b). The relative deviation gives
$\unicode[STIX]{x1D700}_{A}=0.007$
were obtained, as shown in Figure 5(b). The relative deviation gives
![]() $\unicode[STIX]{x1D702}_{A}=|T_{A}-T_{A0}|/T_{A}=1.7\%$
. Details of the calibrations using the four-channel method are listed in Table 1. Also, the spatial chromaticity maps representing the measured temperature using Lamps A and B as the standard are shown in Figures 5(c) and 5(d), respectively. It can be seen from the chromaticity maps that the temperature obtained in each channel has a good spatial consistency. However, the temperatures obtained from different channels exhibit small differences. These differences are likely attributable to the variations in transmission spectra and camera responses of the different channels.
$\unicode[STIX]{x1D702}_{A}=|T_{A}-T_{A0}|/T_{A}=1.7\%$
. Details of the calibrations using the four-channel method are listed in Table 1. Also, the spatial chromaticity maps representing the measured temperature using Lamps A and B as the standard are shown in Figures 5(c) and 5(d), respectively. It can be seen from the chromaticity maps that the temperature obtained in each channel has a good spatial consistency. However, the temperatures obtained from different channels exhibit small differences. These differences are likely attributable to the variations in transmission spectra and camera responses of the different channels.

Figure 5. Spectral radiance data and theoretical Planck fit curve for conditions using (a) Lamp A as the standard or (b) Lamp B as the standard. Spatial chromaticity maps representing the measured temperature using (c) Lamp A as the standard or (d) Lamp B as the standard.
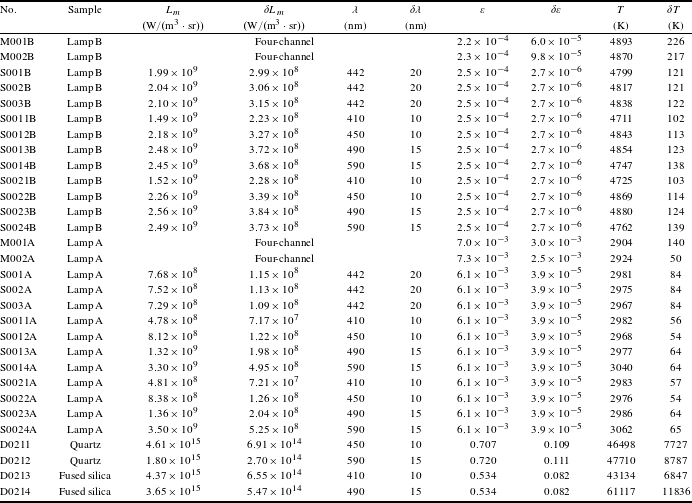
Table 1. Calibration and verification results (measured temperature
![]() $T$
, deviation between the measured temperature and the standard value
$T$
, deviation between the measured temperature and the standard value
![]() $\unicode[STIX]{x1D702}$
) of the SOP system using a single-channel (No. S001–S0024) or multi-channel (No. M001–M002) method are listed in addition to the MCP of the streak camera for each experiment.
$\unicode[STIX]{x1D702}$
) of the SOP system using a single-channel (No. S001–S0024) or multi-channel (No. M001–M002) method are listed in addition to the MCP of the streak camera for each experiment.

2.4 Single-channel method
If the filter in front of the streak camera is a single-channel filter, the temperature of Lamp B can be obtained from Equation (1) when using Lamp A as the standard. Here,
![]() $L_{B}(\unicode[STIX]{x1D706})$
can be directly determined from the formula
$L_{B}(\unicode[STIX]{x1D706})$
can be directly determined from the formula
![]() $L_{B}(\unicode[STIX]{x1D706})=L_{A}(\unicode[STIX]{x1D706})\cdot (t_{A}/t_{B})\cdot (C_{B}/C_{A})$
, where
$L_{B}(\unicode[STIX]{x1D706})=L_{A}(\unicode[STIX]{x1D706})\cdot (t_{A}/t_{B})\cdot (C_{B}/C_{A})$
, where
![]() $\unicode[STIX]{x1D706}$
is the wavelength of the channel and the emissivity can be obtained from the original report of Lamp B, mentioned in Section 2.2. Similarly, the temperature of Lamp A can be measured when adopting Lamp B as the standard using the single-channel method. A series of calibration experiments were conducted at the ‘Shenguang-II’ laser facility platform, as summarized in Table 1. Therefore, the relative deviation
$\unicode[STIX]{x1D706}$
is the wavelength of the channel and the emissivity can be obtained from the original report of Lamp B, mentioned in Section 2.2. Similarly, the temperature of Lamp A can be measured when adopting Lamp B as the standard using the single-channel method. A series of calibration experiments were conducted at the ‘Shenguang-II’ laser facility platform, as summarized in Table 1. Therefore, the relative deviation
![]() $\unicode[STIX]{x1D702}$
reflects that the errors in temperature are less than 6% with the variation of wavelength in our calibrations, which indicates that the system is reliable at different wavelengths.
$\unicode[STIX]{x1D702}$
reflects that the errors in temperature are less than 6% with the variation of wavelength in our calibrations, which indicates that the system is reliable at different wavelengths.
3 Uncertainty and sensitivity analysis of the SOP system
For the multi-channel method, the uncertainty of the temperature and emissivity can be calculated by fitting the error from the least squares method[Reference Pang21]. The calculated uncertainties are listed in Table 2. For the single-channel method, the temperature
![]() $T$
can be obtained from Equation (1), and expressed as
$T$
can be obtained from Equation (1), and expressed as
 $$\begin{eqnarray}T=\frac{hc}{\displaystyle \unicode[STIX]{x1D706}k\ln \left(\frac{2hc^{2}\unicode[STIX]{x1D700}}{L_{m}\unicode[STIX]{x1D706}^{5}}+1\right)},\end{eqnarray}$$
$$\begin{eqnarray}T=\frac{hc}{\displaystyle \unicode[STIX]{x1D706}k\ln \left(\frac{2hc^{2}\unicode[STIX]{x1D700}}{L_{m}\unicode[STIX]{x1D706}^{5}}+1\right)},\end{eqnarray}$$
where
![]() $L_{m}$
is the spectral radiance of the source to be measured. The emissivity
$L_{m}$
is the spectral radiance of the source to be measured. The emissivity
![]() $\unicode[STIX]{x1D700}$
is assumed to be a constant in the calibrations and given by Kirchhoff’s law as
$\unicode[STIX]{x1D700}$
is assumed to be a constant in the calibrations and given by Kirchhoff’s law as
![]() $\unicode[STIX]{x1D700}=1-t-R$
in the shock-wave experiments[Reference Glukhodedov and Kirshanov22]. The transmissivity
$\unicode[STIX]{x1D700}=1-t-R$
in the shock-wave experiments[Reference Glukhodedov and Kirshanov22]. The transmissivity
![]() $t$
is assumed to be zero since the shock-wave front is optically thick[Reference Kormer23]. The reflectivity of the shock front
$t$
is assumed to be zero since the shock-wave front is optically thick[Reference Kormer23]. The reflectivity of the shock front
![]() $R$
can be extracted from the VISAR data[Reference Celliers, Bradley, Collins, Hicks, Boehly and Armstrong24, Reference Zhou, Nellis, Li, Li, Zhao, Liu, Cao, Liu, Xue and Wu25] and was determined by comparing the shock reflectivity to that from the surface of the base material with a known value. Since the variables
$R$
can be extracted from the VISAR data[Reference Celliers, Bradley, Collins, Hicks, Boehly and Armstrong24, Reference Zhou, Nellis, Li, Li, Zhao, Liu, Cao, Liu, Xue and Wu25] and was determined by comparing the shock reflectivity to that from the surface of the base material with a known value. Since the variables
![]() $\unicode[STIX]{x1D700}$
and
$\unicode[STIX]{x1D700}$
and
![]() $L_{m}$
are measured by the VISAR and
$L_{m}$
are measured by the VISAR and
![]() $\unicode[STIX]{x1D706}$
is measured with a spectrophotometer, the three variables are measured independently. Then, the uncertainty in the temperature of the source to be measured can be expressed as
$\unicode[STIX]{x1D706}$
is measured with a spectrophotometer, the three variables are measured independently. Then, the uncertainty in the temperature of the source to be measured can be expressed as
according to the error-transfer rule[Reference Fu, Huang, Ma, Shu, Wu, Ye, He, Gu, Luo and Rong26, Reference Celliers, Collins, Hicks and Eggert27], where
![]() $\unicode[STIX]{x1D6FF}L_{m}$
,
$\unicode[STIX]{x1D6FF}L_{m}$
,
![]() $\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D706}$
and
$\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D706}$
and
![]() $\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D700}$
are the uncertainties of the spectral radiance, wavelength and emissivity, respectively. Because of the complexity of Equation (3), the components under the root sign in the formula have been calculated separately as
$\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D700}$
are the uncertainties of the spectral radiance, wavelength and emissivity, respectively. Because of the complexity of Equation (3), the components under the root sign in the formula have been calculated separately as
 $$\begin{eqnarray}\displaystyle \frac{\unicode[STIX]{x2202}T}{\unicode[STIX]{x2202}L_{m}} & = & \displaystyle \frac{hc}{\displaystyle \unicode[STIX]{x1D706}k\left[\ln \left(\frac{2hc^{2}\unicode[STIX]{x1D700}}{L_{m}\unicode[STIX]{x1D706}^{5}}+1\right)\right]^{2}\left(L_{m}+\frac{\unicode[STIX]{x1D706}^{5}}{2hc^{2}\unicode[STIX]{x1D700}}L_{m}^{2}\right)}\nonumber\\ \displaystyle & = & \displaystyle \frac{T}{\displaystyle \ln \left(\frac{2hc^{2}\unicode[STIX]{x1D700}}{L_{m}\unicode[STIX]{x1D706}^{5}}+1\right)\left(L_{m}+\frac{\unicode[STIX]{x1D706}^{5}}{2hc^{2}\unicode[STIX]{x1D700}}L_{m}^{2}\right)},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \frac{\unicode[STIX]{x2202}T}{\unicode[STIX]{x2202}L_{m}} & = & \displaystyle \frac{hc}{\displaystyle \unicode[STIX]{x1D706}k\left[\ln \left(\frac{2hc^{2}\unicode[STIX]{x1D700}}{L_{m}\unicode[STIX]{x1D706}^{5}}+1\right)\right]^{2}\left(L_{m}+\frac{\unicode[STIX]{x1D706}^{5}}{2hc^{2}\unicode[STIX]{x1D700}}L_{m}^{2}\right)}\nonumber\\ \displaystyle & = & \displaystyle \frac{T}{\displaystyle \ln \left(\frac{2hc^{2}\unicode[STIX]{x1D700}}{L_{m}\unicode[STIX]{x1D706}^{5}}+1\right)\left(L_{m}+\frac{\unicode[STIX]{x1D706}^{5}}{2hc^{2}\unicode[STIX]{x1D700}}L_{m}^{2}\right)},\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle \frac{\unicode[STIX]{x2202}T}{\unicode[STIX]{x2202}\unicode[STIX]{x1D706}} & = & \displaystyle \frac{hc}{k}\left[\frac{5\times 2hc^{2}\unicode[STIX]{x1D700}}{\displaystyle L_{m}\unicode[STIX]{x1D706}^{7}\left[\ln \left(\frac{2hc^{2}\unicode[STIX]{x1D700}}{L_{m}\unicode[STIX]{x1D706}^{5}}+1\right)\right]^{2}\left(\frac{2hc^{2}\unicode[STIX]{x1D700}}{L_{m}\unicode[STIX]{x1D706}^{5}}+1\right)}\right.\nonumber\\ \displaystyle & & \displaystyle -\left.\frac{1}{\displaystyle \unicode[STIX]{x1D706}^{2}\ln \left(\frac{2hc^{2}\unicode[STIX]{x1D700}}{L_{m}\unicode[STIX]{x1D706}^{5}}+1\right)}\right]\nonumber\\ \displaystyle & = & \displaystyle T\left[\frac{5\times 2hc^{2}\unicode[STIX]{x1D700}}{\displaystyle L_{m}\unicode[STIX]{x1D706}^{6}\ln \left(\frac{2hc^{2}\unicode[STIX]{x1D700}}{L_{m}\unicode[STIX]{x1D706}^{5}}+1\right)\left(\frac{2hc^{2}\unicode[STIX]{x1D700}}{L_{m}\unicode[STIX]{x1D706}^{5}}+1\right)}-\frac{1}{\unicode[STIX]{x1D706}}\right],\nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \frac{\unicode[STIX]{x2202}T}{\unicode[STIX]{x2202}\unicode[STIX]{x1D706}} & = & \displaystyle \frac{hc}{k}\left[\frac{5\times 2hc^{2}\unicode[STIX]{x1D700}}{\displaystyle L_{m}\unicode[STIX]{x1D706}^{7}\left[\ln \left(\frac{2hc^{2}\unicode[STIX]{x1D700}}{L_{m}\unicode[STIX]{x1D706}^{5}}+1\right)\right]^{2}\left(\frac{2hc^{2}\unicode[STIX]{x1D700}}{L_{m}\unicode[STIX]{x1D706}^{5}}+1\right)}\right.\nonumber\\ \displaystyle & & \displaystyle -\left.\frac{1}{\displaystyle \unicode[STIX]{x1D706}^{2}\ln \left(\frac{2hc^{2}\unicode[STIX]{x1D700}}{L_{m}\unicode[STIX]{x1D706}^{5}}+1\right)}\right]\nonumber\\ \displaystyle & = & \displaystyle T\left[\frac{5\times 2hc^{2}\unicode[STIX]{x1D700}}{\displaystyle L_{m}\unicode[STIX]{x1D706}^{6}\ln \left(\frac{2hc^{2}\unicode[STIX]{x1D700}}{L_{m}\unicode[STIX]{x1D706}^{5}}+1\right)\left(\frac{2hc^{2}\unicode[STIX]{x1D700}}{L_{m}\unicode[STIX]{x1D706}^{5}}+1\right)}-\frac{1}{\unicode[STIX]{x1D706}}\right],\nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle \frac{\unicode[STIX]{x2202}T}{\unicode[STIX]{x2202}\unicode[STIX]{x1D700}} & = & \displaystyle -\frac{hc\times 2hc^{2}}{\displaystyle \unicode[STIX]{x1D706}^{6}kL_{m}\left[\ln \left(\frac{2hc^{2}\unicode[STIX]{x1D700}}{L_{m}\unicode[STIX]{x1D706}^{5}}+1\right)\right]^{2}\left(\frac{2hc^{2}\unicode[STIX]{x1D700}}{L_{m}\unicode[STIX]{x1D706}^{5}}+1\right)}\nonumber\\ \displaystyle & = & \displaystyle -T\frac{2hc^{2}}{\displaystyle L_{m}\unicode[STIX]{x1D706}^{5}\ln \left(\frac{2hc^{2}\unicode[STIX]{x1D700}}{L_{m}\unicode[STIX]{x1D706}^{5}}+1\right)\left(\frac{2hc^{2}\unicode[STIX]{x1D700}}{L_{m}\unicode[STIX]{x1D706}^{5}}+1\right)}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \frac{\unicode[STIX]{x2202}T}{\unicode[STIX]{x2202}\unicode[STIX]{x1D700}} & = & \displaystyle -\frac{hc\times 2hc^{2}}{\displaystyle \unicode[STIX]{x1D706}^{6}kL_{m}\left[\ln \left(\frac{2hc^{2}\unicode[STIX]{x1D700}}{L_{m}\unicode[STIX]{x1D706}^{5}}+1\right)\right]^{2}\left(\frac{2hc^{2}\unicode[STIX]{x1D700}}{L_{m}\unicode[STIX]{x1D706}^{5}}+1\right)}\nonumber\\ \displaystyle & = & \displaystyle -T\frac{2hc^{2}}{\displaystyle L_{m}\unicode[STIX]{x1D706}^{5}\ln \left(\frac{2hc^{2}\unicode[STIX]{x1D700}}{L_{m}\unicode[STIX]{x1D706}^{5}}+1\right)\left(\frac{2hc^{2}\unicode[STIX]{x1D700}}{L_{m}\unicode[STIX]{x1D706}^{5}}+1\right)}.\end{eqnarray}$$
Substituting Equations (4)–(6) into Equation (3),
![]() $\unicode[STIX]{x1D6FF}T$
can be expressed as
$\unicode[STIX]{x1D6FF}T$
can be expressed as
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6FF}T & = & \displaystyle T\nonumber\\ \displaystyle & & \displaystyle \times \,\left\{\frac{(\unicode[STIX]{x1D6FF}L_{m})^{2}}{\displaystyle \left[\ln \left(\frac{2hc^{2}\unicode[STIX]{x1D700}}{L_{m}\unicode[STIX]{x1D706}^{5}}+1\right)\right]^{2}\left(L_{m}+\frac{\unicode[STIX]{x1D706}^{5}L_{m}^{2}}{2hc^{2}\unicode[STIX]{x1D700}}\right)^{2}}\right.\nonumber\\ \displaystyle & & \displaystyle +\,\left[\frac{5\times 2hc^{2}\unicode[STIX]{x1D700}}{\displaystyle L_{m}\unicode[STIX]{x1D706}^{6}\ln \left(\frac{2hc^{2}\unicode[STIX]{x1D700}}{L_{m}\unicode[STIX]{x1D706}^{5}}+1\right)\left(\frac{2hc^{2}\unicode[STIX]{x1D700}}{L_{m}\unicode[STIX]{x1D706}^{5}}+1\right)}-\frac{1}{\unicode[STIX]{x1D706}}\right]^{2}(\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D706})^{2}\nonumber\\ \displaystyle & & \displaystyle +\left.\left[\frac{2hc^{2}(\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D700})^{4}}{\displaystyle L_{m}\unicode[STIX]{x1D706}^{5}\ln \left(\frac{2hc^{2}\unicode[STIX]{x1D700}}{L_{m}\unicode[STIX]{x1D706}^{5}}+1\right)\left(\frac{2hc^{2}\unicode[STIX]{x1D700}}{L_{m}\unicode[STIX]{x1D706}^{5}}+1\right)}\right]^{2}\right\}^{1/2}.\nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6FF}T & = & \displaystyle T\nonumber\\ \displaystyle & & \displaystyle \times \,\left\{\frac{(\unicode[STIX]{x1D6FF}L_{m})^{2}}{\displaystyle \left[\ln \left(\frac{2hc^{2}\unicode[STIX]{x1D700}}{L_{m}\unicode[STIX]{x1D706}^{5}}+1\right)\right]^{2}\left(L_{m}+\frac{\unicode[STIX]{x1D706}^{5}L_{m}^{2}}{2hc^{2}\unicode[STIX]{x1D700}}\right)^{2}}\right.\nonumber\\ \displaystyle & & \displaystyle +\,\left[\frac{5\times 2hc^{2}\unicode[STIX]{x1D700}}{\displaystyle L_{m}\unicode[STIX]{x1D706}^{6}\ln \left(\frac{2hc^{2}\unicode[STIX]{x1D700}}{L_{m}\unicode[STIX]{x1D706}^{5}}+1\right)\left(\frac{2hc^{2}\unicode[STIX]{x1D700}}{L_{m}\unicode[STIX]{x1D706}^{5}}+1\right)}-\frac{1}{\unicode[STIX]{x1D706}}\right]^{2}(\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D706})^{2}\nonumber\\ \displaystyle & & \displaystyle +\left.\left[\frac{2hc^{2}(\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D700})^{4}}{\displaystyle L_{m}\unicode[STIX]{x1D706}^{5}\ln \left(\frac{2hc^{2}\unicode[STIX]{x1D700}}{L_{m}\unicode[STIX]{x1D706}^{5}}+1\right)\left(\frac{2hc^{2}\unicode[STIX]{x1D700}}{L_{m}\unicode[STIX]{x1D706}^{5}}+1\right)}\right]^{2}\right\}^{1/2}.\nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
The relative uncertainty of
![]() $T$
can be expressed as
$T$
can be expressed as
 $$\begin{eqnarray}\displaystyle \frac{\unicode[STIX]{x1D6FF}T}{T} & = & \displaystyle \left\{\frac{(\unicode[STIX]{x1D6FF}L_{m})^{2}}{\displaystyle \left[\ln \left(\frac{2hc^{2}\unicode[STIX]{x1D700}}{L_{m}\unicode[STIX]{x1D706}^{5}}+1\right)\right]^{2}\left(L_{m}+\frac{\unicode[STIX]{x1D706}^{5}L_{m}^{2}}{2hc^{2}\unicode[STIX]{x1D700}}\right)^{2}}\right.\nonumber\\ \displaystyle & & \displaystyle +\,\left[\frac{5\times 2hc^{2}\unicode[STIX]{x1D700}}{\displaystyle L_{m}\unicode[STIX]{x1D706}^{6}\ln \left(\frac{2hc^{2}\unicode[STIX]{x1D700}}{L_{m}\unicode[STIX]{x1D706}^{5}}+1\right)\left(\frac{2hc^{2}\unicode[STIX]{x1D700}}{L_{m}\unicode[STIX]{x1D706}^{5}}+1\right)}-\frac{1}{\unicode[STIX]{x1D706}}\right]^{2}(\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D706})^{2}\nonumber\\ \displaystyle & & \displaystyle +\left.\left[\frac{2hc^{2}(\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D700})^{4}}{\displaystyle L_{m}\unicode[STIX]{x1D706}^{5}\ln \left(\frac{2hc^{2}\unicode[STIX]{x1D700}}{L_{m}\unicode[STIX]{x1D706}^{5}}+1\right)\left(\frac{2hc^{2}\unicode[STIX]{x1D700}}{L_{m}\unicode[STIX]{x1D706}^{5}}+1\right)}\right]^{2}\right\}^{1/2}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \frac{\unicode[STIX]{x1D6FF}T}{T} & = & \displaystyle \left\{\frac{(\unicode[STIX]{x1D6FF}L_{m})^{2}}{\displaystyle \left[\ln \left(\frac{2hc^{2}\unicode[STIX]{x1D700}}{L_{m}\unicode[STIX]{x1D706}^{5}}+1\right)\right]^{2}\left(L_{m}+\frac{\unicode[STIX]{x1D706}^{5}L_{m}^{2}}{2hc^{2}\unicode[STIX]{x1D700}}\right)^{2}}\right.\nonumber\\ \displaystyle & & \displaystyle +\,\left[\frac{5\times 2hc^{2}\unicode[STIX]{x1D700}}{\displaystyle L_{m}\unicode[STIX]{x1D706}^{6}\ln \left(\frac{2hc^{2}\unicode[STIX]{x1D700}}{L_{m}\unicode[STIX]{x1D706}^{5}}+1\right)\left(\frac{2hc^{2}\unicode[STIX]{x1D700}}{L_{m}\unicode[STIX]{x1D706}^{5}}+1\right)}-\frac{1}{\unicode[STIX]{x1D706}}\right]^{2}(\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D706})^{2}\nonumber\\ \displaystyle & & \displaystyle +\left.\left[\frac{2hc^{2}(\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D700})^{4}}{\displaystyle L_{m}\unicode[STIX]{x1D706}^{5}\ln \left(\frac{2hc^{2}\unicode[STIX]{x1D700}}{L_{m}\unicode[STIX]{x1D706}^{5}}+1\right)\left(\frac{2hc^{2}\unicode[STIX]{x1D700}}{L_{m}\unicode[STIX]{x1D706}^{5}}+1\right)}\right]^{2}\right\}^{1/2}.\end{eqnarray}$$
Thus, to obtain
![]() $\unicode[STIX]{x1D6FF}T$
, the components
$\unicode[STIX]{x1D6FF}T$
, the components
![]() $\unicode[STIX]{x1D6FF}L_{m}$
,
$\unicode[STIX]{x1D6FF}L_{m}$
,
![]() $\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D706}$
, and
$\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D706}$
, and
![]() $\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D700}$
need to be calculated independently.
$\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D700}$
need to be calculated independently.
The values of
![]() $\unicode[STIX]{x1D6FF}L_{m}$
can be obtained from
$\unicode[STIX]{x1D6FF}L_{m}$
can be obtained from
![]() $L_{m}=L_{s}\cdot (t_{s}/t_{m})\cdot (C_{m}/C_{s})$
, as mentioned in Section 2.2, according to the error-transfer formula, where the subscripts
$L_{m}=L_{s}\cdot (t_{s}/t_{m})\cdot (C_{m}/C_{s})$
, as mentioned in Section 2.2, according to the error-transfer formula, where the subscripts
![]() $m$
and
$m$
and
![]() $s$
represent the source to be measured and standard source, respectively. Since
$s$
represent the source to be measured and standard source, respectively. Since
![]() $t_{s}$
and
$t_{s}$
and
![]() $t_{m}$
are constants related to the streak camera, the uncertainty in the spectral radiance can be expressed as
$t_{m}$
are constants related to the streak camera, the uncertainty in the spectral radiance can be expressed as
 $$\begin{eqnarray}\displaystyle & & \displaystyle \unicode[STIX]{x1D6FF}L_{m}=\sqrt{\left(\frac{\unicode[STIX]{x2202}L_{m}}{\unicode[STIX]{x2202}C_{m}}\right)^{2}\left(\unicode[STIX]{x1D6FF}C_{m}\right)^{2}+\left(\frac{\unicode[STIX]{x2202}L_{m}}{\unicode[STIX]{x2202}C_{s}}\right)^{2}\left(\unicode[STIX]{x1D6FF}C_{s}\right)^{2}+\left(\frac{\unicode[STIX]{x2202}L_{m}}{\unicode[STIX]{x2202}L_{s}}\right)^{2}\left(\unicode[STIX]{x1D6FF}L_{s}\right)^{2}}\nonumber\\ \displaystyle & & \displaystyle \quad =L_{m}\sqrt{\left(\frac{\unicode[STIX]{x1D6FF}C_{m}}{C_{m}}\right)^{2}+\left(\frac{\unicode[STIX]{x1D6FF}C_{s}}{C_{s}}\right)^{2}+\left(\frac{\unicode[STIX]{x1D6FF}L_{s}}{L_{s}}\right)^{2}},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \unicode[STIX]{x1D6FF}L_{m}=\sqrt{\left(\frac{\unicode[STIX]{x2202}L_{m}}{\unicode[STIX]{x2202}C_{m}}\right)^{2}\left(\unicode[STIX]{x1D6FF}C_{m}\right)^{2}+\left(\frac{\unicode[STIX]{x2202}L_{m}}{\unicode[STIX]{x2202}C_{s}}\right)^{2}\left(\unicode[STIX]{x1D6FF}C_{s}\right)^{2}+\left(\frac{\unicode[STIX]{x2202}L_{m}}{\unicode[STIX]{x2202}L_{s}}\right)^{2}\left(\unicode[STIX]{x1D6FF}L_{s}\right)^{2}}\nonumber\\ \displaystyle & & \displaystyle \quad =L_{m}\sqrt{\left(\frac{\unicode[STIX]{x1D6FF}C_{m}}{C_{m}}\right)^{2}+\left(\frac{\unicode[STIX]{x1D6FF}C_{s}}{C_{s}}\right)^{2}+\left(\frac{\unicode[STIX]{x1D6FF}L_{s}}{L_{s}}\right)^{2}},\end{eqnarray}$$
where
![]() $\unicode[STIX]{x1D6FF}C/C$
is
$\unicode[STIX]{x1D6FF}C/C$
is
![]() ${\sim}10\%$
according to the standard deviation of the streak camera, and
${\sim}10\%$
according to the standard deviation of the streak camera, and
![]() $\unicode[STIX]{x1D6FF}L_{s}/L_{s}$
is
$\unicode[STIX]{x1D6FF}L_{s}/L_{s}$
is
![]() ${\sim}5\%$
according to the calibration report of the standard lamps. Therefore, the relative uncertainty of the spectral radiance
${\sim}5\%$
according to the calibration report of the standard lamps. Therefore, the relative uncertainty of the spectral radiance
![]() $\unicode[STIX]{x1D6FF}L_{m}/L_{m}$
is
$\unicode[STIX]{x1D6FF}L_{m}/L_{m}$
is
![]() ${\sim}15\%$
.
${\sim}15\%$
.
The values of
![]() $\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D706}$
can be measured by the spectrophotometer, which manifests as the maximum deviation from the central wavelength. Then, the relative uncertainty
$\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D706}$
can be measured by the spectrophotometer, which manifests as the maximum deviation from the central wavelength. Then, the relative uncertainty
![]() $\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D706}/\unicode[STIX]{x1D706}$
can be obtained as well. For filters with a large bandwidth, the error is also potentially significant.
$\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D706}/\unicode[STIX]{x1D706}$
can be obtained as well. For filters with a large bandwidth, the error is also potentially significant.
In calibration experiments,
![]() $\unicode[STIX]{x1D700}$
,
$\unicode[STIX]{x1D700}$
,
![]() $\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D700}$
and
$\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D700}$
and
![]() $\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D700}/\unicode[STIX]{x1D700}$
can be obtained directly from the original calibration report of the standard lamps. However, in shock-wave experiments,
$\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D700}/\unicode[STIX]{x1D700}$
can be obtained directly from the original calibration report of the standard lamps. However, in shock-wave experiments,
![]() $\unicode[STIX]{x1D700}=1-R_{\text{SOP}}$
, which gives
$\unicode[STIX]{x1D700}=1-R_{\text{SOP}}$
, which gives
![]() $\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D700}=\unicode[STIX]{x1D6FF}R_{\text{SOP}}$
. Since
$\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D700}=\unicode[STIX]{x1D6FF}R_{\text{SOP}}$
. Since
![]() $R_{\text{SOP}}=R_{\text{VISAR}}-d=R_{\text{base}}C_{\text{VISAR}}/C_{\text{base}}-d$
, where
$R_{\text{SOP}}=R_{\text{VISAR}}-d=R_{\text{base}}C_{\text{VISAR}}/C_{\text{base}}-d$
, where
![]() $d$
is the difference in reflectivity between the SOP channel and the VISAR probe beam, it can be regarded as a constant in a certain state[Reference He, Jia, Zhang, Luo, Huang, Shu, Fang, Ye, Xie, Xia and Fu10, Reference He, Shu, Huang, Zhang, Jia, Zhang, Tu, Wang, Ye, Xie, Fang, Pei and Fu11].
$d$
is the difference in reflectivity between the SOP channel and the VISAR probe beam, it can be regarded as a constant in a certain state[Reference He, Jia, Zhang, Luo, Huang, Shu, Fang, Ye, Xie, Xia and Fu10, Reference He, Shu, Huang, Zhang, Jia, Zhang, Tu, Wang, Ye, Xie, Fang, Pei and Fu11].
![]() $R_{\text{base}}$
is the reflectivity of base material, while
$R_{\text{base}}$
is the reflectivity of base material, while
![]() $C_{\text{VISAR}}$
and
$C_{\text{VISAR}}$
and
![]() $C_{\text{base}}$
are the camera counts of the shocked material and base material, respectively. The uncertainty of the emissivity in the shock-wave experiments can be expressed as
$C_{\text{base}}$
are the camera counts of the shocked material and base material, respectively. The uncertainty of the emissivity in the shock-wave experiments can be expressed as
 $$\begin{eqnarray}\displaystyle & & \displaystyle \unicode[STIX]{x1D6FF}\unicode[STIX]{x1D700}=\unicode[STIX]{x1D6FF}R_{\text{SOP}}=\unicode[STIX]{x1D6FF}R_{\text{VISAR}}\nonumber\\ \displaystyle & & \displaystyle \quad =R_{\text{VISAR}}\sqrt{\left(\frac{\unicode[STIX]{x1D6FF}C_{\text{VISAR}}}{C_{\text{VISAR}}}\right)^{2}+\left(\frac{\unicode[STIX]{x1D6FF}C_{\text{base}}}{C_{\text{base}}}\right)^{2}+\left(\frac{\unicode[STIX]{x1D6FF}R_{\text{base}}}{R_{\text{base}}}\right)^{2}},\nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \unicode[STIX]{x1D6FF}\unicode[STIX]{x1D700}=\unicode[STIX]{x1D6FF}R_{\text{SOP}}=\unicode[STIX]{x1D6FF}R_{\text{VISAR}}\nonumber\\ \displaystyle & & \displaystyle \quad =R_{\text{VISAR}}\sqrt{\left(\frac{\unicode[STIX]{x1D6FF}C_{\text{VISAR}}}{C_{\text{VISAR}}}\right)^{2}+\left(\frac{\unicode[STIX]{x1D6FF}C_{\text{base}}}{C_{\text{base}}}\right)^{2}+\left(\frac{\unicode[STIX]{x1D6FF}R_{\text{base}}}{R_{\text{base}}}\right)^{2}},\nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
where
![]() $\unicode[STIX]{x1D6FF}C_{\text{VISAR}}/C_{\text{VISAR}}\approx \unicode[STIX]{x1D6FF}C_{\text{base}}/C_{\text{base}}$
is
$\unicode[STIX]{x1D6FF}C_{\text{VISAR}}/C_{\text{VISAR}}\approx \unicode[STIX]{x1D6FF}C_{\text{base}}/C_{\text{base}}$
is
![]() ${\sim}10\%$
, and
${\sim}10\%$
, and
![]() $R_{\text{base}}$
,
$R_{\text{base}}$
,
![]() $\unicode[STIX]{x1D6FF}R_{\text{base}}$
, and
$\unicode[STIX]{x1D6FF}R_{\text{base}}$
, and
![]() $\unicode[STIX]{x1D6FF}R_{\text{base}}/R_{\text{base}}$
should be measured by the target group.
$\unicode[STIX]{x1D6FF}R_{\text{base}}/R_{\text{base}}$
should be measured by the target group.
Therefore, the uncertainty and relative uncertainty of the temperature to be measured,
![]() $\unicode[STIX]{x1D6FF}T$
and
$\unicode[STIX]{x1D6FF}T$
and
![]() $\unicode[STIX]{x1D6FF}T/T$
, can be calculated by substituting
$\unicode[STIX]{x1D6FF}T/T$
, can be calculated by substituting
![]() $\unicode[STIX]{x1D6FF}L_{m}$
,
$\unicode[STIX]{x1D6FF}L_{m}$
,
![]() $\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D706}$
and
$\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D706}$
and
![]() $\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D700}$
into Equations (7) and (8). The calculated uncertainties in the calibrations and shock-wave experiments are listed in Table 2.
$\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D700}$
into Equations (7) and (8). The calculated uncertainties in the calibrations and shock-wave experiments are listed in Table 2.
Table 2. Variables and their uncertainties in the calibrations and shock-wave experiments. Samples for the calibrations using a single-channel begin with an S; samples for calibrations using a multi-channel begin with an M; and samples for the shock-wave experiments begin with a D. In particular, the
![]() $L_{m}$
,
$L_{m}$
,
![]() $\unicode[STIX]{x1D700}$
, and
$\unicode[STIX]{x1D700}$
, and
![]() $T$
of the shock-wave experiments refer to values at the interface of the sample and base material.
$T$
of the shock-wave experiments refer to values at the interface of the sample and base material.
The precision of the temperature calculation can be improved by analyzing its sensitivity to the variables
![]() $L_{m}$
,
$L_{m}$
,
![]() $\unicode[STIX]{x1D706}$
and
$\unicode[STIX]{x1D706}$
and
![]() $\unicode[STIX]{x1D700}$
. The sensitivity
$\unicode[STIX]{x1D700}$
. The sensitivity
![]() $S$
can be defined as
$S$
can be defined as
where
![]() $X$
refers to three variables that affect the temperature calculation. Figure 6(a) shows the relationship between
$X$
refers to three variables that affect the temperature calculation. Figure 6(a) shows the relationship between
![]() $\unicode[STIX]{x0394}T/T$
and
$\unicode[STIX]{x0394}T/T$
and
![]() $\unicode[STIX]{x0394}X/X$
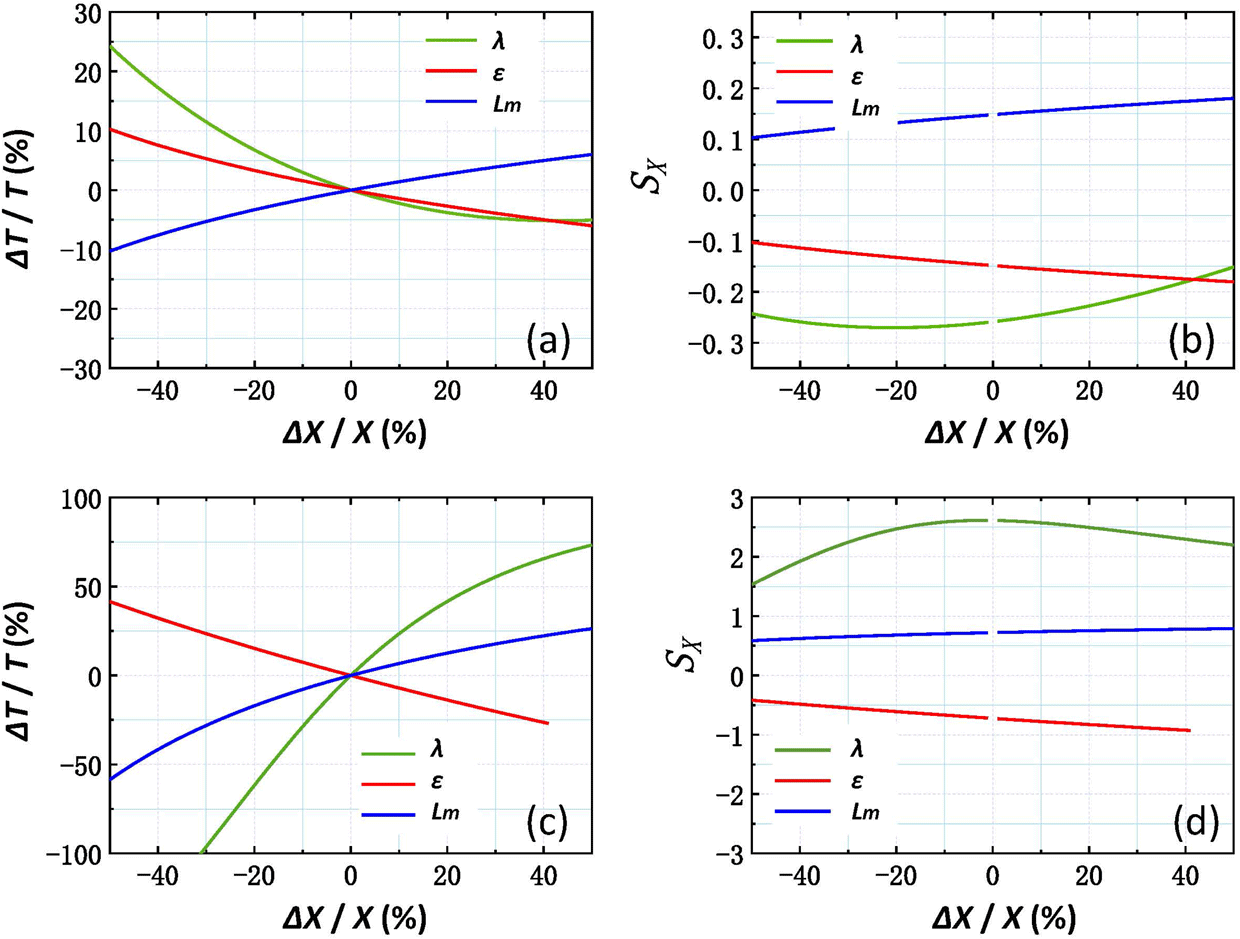
, while Figure 6(b) shows the temperature sensitivity of the three variables in a single calibration experiment. The results show that the wavelength
$\unicode[STIX]{x0394}X/X$
, while Figure 6(b) shows the temperature sensitivity of the three variables in a single calibration experiment. The results show that the wavelength
![]() $\unicode[STIX]{x1D706}$
is the most sensitive to the temperature calculation within the vicinity of the measured value of thousands of kelvin. The temperature sensitivities of the emissivity and radiation intensity are smaller than that of the wavelength, and are similar to each other, but in opposite directions.
$\unicode[STIX]{x1D706}$
is the most sensitive to the temperature calculation within the vicinity of the measured value of thousands of kelvin. The temperature sensitivities of the emissivity and radiation intensity are smaller than that of the wavelength, and are similar to each other, but in opposite directions.
For the shock-wave experiments shown in Figures 6(c) and 6(d), all of the variables are far more sensitive to the temperature than during the calibration, leading to greater errors in the temperature calculation. The wavelength is the most sensitive variable to the temperature in the shock-wave experiments but with a direction opposite to that during the calibration. The sensitivities of the two other variables are similar in the vicinity of the measured value, but in opposite directions as well. Although the wavelength seems to be the most sensitive factor, its uncertainty is the smallest of the three variables in the shock-wave experiments according to Table 2. Concretely, for the shock-wave experiment D0211,
![]() $\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D706}/\unicode[STIX]{x1D706}\sim 2.2\%$
, where
$\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D706}/\unicode[STIX]{x1D706}\sim 2.2\%$
, where
![]() $S_{\unicode[STIX]{x1D706}}\sim 2.6$
and
$S_{\unicode[STIX]{x1D706}}\sim 2.6$
and
![]() $\unicode[STIX]{x0394}T/T\sim 5.7\%$
. Also,
$\unicode[STIX]{x0394}T/T\sim 5.7\%$
. Also,
![]() $\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D700}/\unicode[STIX]{x1D700}\sim 15\%$
, where
$\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D700}/\unicode[STIX]{x1D700}\sim 15\%$
, where
![]() $S_{\unicode[STIX]{x1D700}}\sim -0.8$
and
$S_{\unicode[STIX]{x1D700}}\sim -0.8$
and
![]() $\unicode[STIX]{x0394}T/T\sim -10\%$
and
$\unicode[STIX]{x0394}T/T\sim -10\%$
and
![]() $\unicode[STIX]{x1D6FF}L_{m}/L_{m}\sim 15\%$
, where
$\unicode[STIX]{x1D6FF}L_{m}/L_{m}\sim 15\%$
, where
![]() $S_{L}\sim 0.75$
and
$S_{L}\sim 0.75$
and
![]() $\unicode[STIX]{x0394}T/T\sim 9.7\%$
. In general, even if
$\unicode[STIX]{x0394}T/T\sim 9.7\%$
. In general, even if
![]() $\unicode[STIX]{x1D706}$
is the most sensitive variable,
$\unicode[STIX]{x1D706}$
is the most sensitive variable,
![]() $\unicode[STIX]{x1D700}$
and
$\unicode[STIX]{x1D700}$
and
![]() $L_{m}$
have greater influence on the temperature calculation. The uncertainty of
$L_{m}$
have greater influence on the temperature calculation. The uncertainty of
![]() $L_{m}$
originates from the performance of the streak camera, while the uncertainty of
$L_{m}$
originates from the performance of the streak camera, while the uncertainty of
![]() $\unicode[STIX]{x1D700}$
mainly arises from the reflectivity measurement. Thus, improving the precision of the reflectivity measurement is the key to improving the precision of the temperature calculation.
$\unicode[STIX]{x1D700}$
mainly arises from the reflectivity measurement. Thus, improving the precision of the reflectivity measurement is the key to improving the precision of the temperature calculation.

Figure 6. Relationship between
![]() $\unicode[STIX]{x0394}T/T$
and
$\unicode[STIX]{x0394}T/T$
and
![]() $\unicode[STIX]{x0394}X/X$
and the sensitivity curve of the calibration (No. S003B, (a) and (b)) and shock-wave experiment (No. D0211, (c) and (d)).
$\unicode[STIX]{x0394}X/X$
and the sensitivity curve of the calibration (No. S003B, (a) and (b)) and shock-wave experiment (No. D0211, (c) and (d)).
4 Applications in shock experiments
To verify the reliability of the SOP system for temperature measurements at tens of thousands of kelvin, quartz was selected as the material to be studied, owing to its abundant research data. A series of laser-induced shock experiments were conducted at the ‘Shenguang-II’ laser facility. Decaying shock waves were generated by ablation of the thin plastic layers (CH and CHBr) backing the sample. Laser energies of up to 1000 J were delivered at 351 nm. The temporal profile of the laser was nearly square, with an FWHM of
![]() ${\sim}2~\text{ns}$
. A lens-array (LA) system[Reference Deng, Liang, Chen, Yu and Ma28, Reference Fu, Gu, Wu and Wang29] was used to smooth the laser beam to obtain a flat-topped profile in the focal plane. The focal spot had a
${\sim}2~\text{ns}$
. A lens-array (LA) system[Reference Deng, Liang, Chen, Yu and Ma28, Reference Fu, Gu, Wu and Wang29] was used to smooth the laser beam to obtain a flat-topped profile in the focal plane. The focal spot had a
![]() $1~\text{mm}\times 0.7~\text{mm}$
rectangular region, and the resulting intensities were
$1~\text{mm}\times 0.7~\text{mm}$
rectangular region, and the resulting intensities were
![]() ${\sim}10^{14}~\text{W}/\text{cm}^{2}$
.
${\sim}10^{14}~\text{W}/\text{cm}^{2}$
.
Standard laser-shock diagnostics, including SOP and VISAR, were employed. The VISAR (660 nm) was applied for simultaneous diagnostics with the SOP for the free surface velocity and optical reflectivity. The diagnostic systems had a temporal resolution of
![]() ${\sim}50~\text{ps}$
and a spatial resolution of
${\sim}50~\text{ps}$
and a spatial resolution of
![]() ${\sim}7~\unicode[STIX]{x03BC}\text{m}$
.
${\sim}7~\unicode[STIX]{x03BC}\text{m}$
.

Figure 7. (a) Schematic of the target; (b) VISAR line-image record; (c) SOP image record; (d) a comparison of the reflectivity as a function of shock velocity in quartz and fused silica by Hicks et al. [Reference Hicks, Boehly, Eggert, Miller, Celliers and Collins2, Reference Hicks, Boehly, Celliers, Eggert, Vianello, Meyerhofer and Collins6]; and (e) a comparison of the measured temperature as a function of shock velocity in quartz by Hicks et al. (solid pink diamonds), the Sesame model (solid cyan line), and this work (solid blue circles for fused silica and solid red circles for quartz).
Figures 7(a)–7(c) show the target and diagnostic images of one of the shock experiments. The shock velocity, reflectivity and self-emission of the sample were obtained from the VISAR and SOP system. Figures 7(d) and 7(e) show the reflectivity and the temperature as functions of the shock velocity in both quartz and fused silica. The velocities were measured to
![]() ${\sim}1\%$
precision in our experiments[Reference Shu, Fu, Huang, Fang, Wang, Ye, Xie, Zhou and Long8]. Our reflectivity curve of quartz was almost coincident with Hicks’ data[Reference Hicks, Boehly, Eggert, Miller, Celliers and Collins2], except for the smaller data around
${\sim}1\%$
precision in our experiments[Reference Shu, Fu, Huang, Fang, Wang, Ye, Xie, Zhou and Long8]. Our reflectivity curve of quartz was almost coincident with Hicks’ data[Reference Hicks, Boehly, Eggert, Miller, Celliers and Collins2], except for the smaller data around
![]() $18~\text{km}/\text{s}$
. As for the reflectivity of fused silica, our data below
$18~\text{km}/\text{s}$
. As for the reflectivity of fused silica, our data below
![]() $18~\text{km}/\text{s}$
seemed to agree with Hicks’ data. But the saturated reflectivity was
$18~\text{km}/\text{s}$
seemed to agree with Hicks’ data. But the saturated reflectivity was
![]() ${\sim}25\%$
higher than Hicks’ data, which might be due to differences in materials such as density and surface roughness. The size of the uncertainty in the calculated temperature was 15%–18% according to Section 3. Compared with previous experiments, the temperature of the quartz here was nearly consistent with Hicks’ data, but slightly lower at shock velocities below
${\sim}25\%$
higher than Hicks’ data, which might be due to differences in materials such as density and surface roughness. The size of the uncertainty in the calculated temperature was 15%–18% according to Section 3. Compared with previous experiments, the temperature of the quartz here was nearly consistent with Hicks’ data, but slightly lower at shock velocities below
![]() $20~\text{km}/\text{s}$
. In fact, since the acquired reflectivity was continuous data in one shot, the error of reflectivity measured by VISAR intensity would become gradually larger with the attenuation of the shock wave and the influence of the lateral release wave. This is probably the reason for the lower temperature of quartz around
$20~\text{km}/\text{s}$
. In fact, since the acquired reflectivity was continuous data in one shot, the error of reflectivity measured by VISAR intensity would become gradually larger with the attenuation of the shock wave and the influence of the lateral release wave. This is probably the reason for the lower temperature of quartz around
![]() $18~\text{km}/\text{s}$
in our experiments. Analysis in Section 3 does not consider the influence of the release wave on reflectivity intensity, which will also lead to differences of the final temperature results. In the future, there is still space and necessity to study the error of the gray body hypothesis itself and the influence of the release wave on reflectivity. Also, the temperature of fused silica was
$18~\text{km}/\text{s}$
in our experiments. Analysis in Section 3 does not consider the influence of the release wave on reflectivity intensity, which will also lead to differences of the final temperature results. In the future, there is still space and necessity to study the error of the gray body hypothesis itself and the influence of the release wave on reflectivity. Also, the temperature of fused silica was
![]() ${\sim}25\%$
higher than that of quartz. This observation is also consistent with Hicks’ results. However, both experimental data on the laser are
${\sim}25\%$
higher than that of quartz. This observation is also consistent with Hicks’ results. However, both experimental data on the laser are
![]() ${\sim}28\%$
lower than in the Sesame model[Reference Lyon and Johnson30]. Therefore, the measured temperatures of the standard materials in our experiments agreed fairly well with those obtained in previous works, which could be evidence of the reliability of the SOP system at tens of thousands of kelvin.
${\sim}28\%$
lower than in the Sesame model[Reference Lyon and Johnson30]. Therefore, the measured temperatures of the standard materials in our experiments agreed fairly well with those obtained in previous works, which could be evidence of the reliability of the SOP system at tens of thousands of kelvin.
5 Conclusions
Two calibrated Planckian radiators with different color temperatures were used for calibration and verification of the SOP system. They are regarded as both the known standard and unknown source for each other in the SOP system. The SOP system was calibrated using both multi-channel and single-channel methods. To verify the reliability of the SOP system, the relative deviation between the measured data and the standard value was calibrated for. Also, a method to analyze the uncertainty and sensitivity of the SOP system was proposed. To verify the reliability of the SOP system for temperature measurements at tens of thousands of kelvin, a series of laser-induced shock experiments were conducted at the ‘Shenguang-II’ laser facility. The measured temperature of quartz in our experiments agreed with previous works fairly well, which could be evidence of the reliability of the SOP system.
Acknowledgements
We gratefully acknowledge the valuable support for the experiments by the ‘Shenguang-II’ technical crews. This work was supported by the National Key R&D Program of China (No. 2017YFA0403200) and the Science Challenge Project (No. TZ2016001).