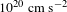1 Introduction
Controlled fusion reaction for energy production is so highly attractive that enormous research was invested during the past 60 years focusing on the reaction of heavy and super-heavy hydrogen, deuterium D and tritium T, respectively. Impressive advances were achieved while it is well evident that the aimed power station is still far away in the future. A special problem for DT fusion is that the generation of neutrons apart from the clean helium resulted in the statement (see Nature, citation Butler[Reference Hora, Korn, Giuffrida, Margarone, Picciotto, Krasa, Jungwirth, Ullschmied, Lalousis, Eliezer, Miley, Moustaizis and Mourou1]) that the magnetic confinement option International Thermonuclear Experimental Reactor (ITER) will result in the ‘hottest radioactive working environment on earth’.
The fusion reaction of hydrogen (protons) with 11B (HB11) initially did not at all show primary neutron generation[Reference Oliphant and Rutherford2] while further any side reaction produced less tolerable radioactivity per produced energy[Reference Weaver, Zimmerman and Wood3]. This takes into account the extreme non-equilibrium conditions. The energy generated by the HB11 reaction[Reference Weaver, Zimmerman and Wood3]
was measured even before the DT fusion reaction was discovered. It was early realized that the HB11 reaction is extremely more difficult than DT fusion. When using nanosecond laser pulses for compression, heating and ignition of HB11, densities above 100.000 times of solid are needed[Reference Kouhi, Ghoraneviss, Malekynia, Hora, Miley, Sari, Azizi and Razavipour4]. Compressing DT to the order of the thousand times of solid state has been verified[Reference Azechi, Jitsuno, Kanabe, Katayama, Mima, Miyanaga, Nakai, Nakai, Nakaichi, Nishiguchi, Norreys, Setsuhara, Takagi, Yamanaka and Yamanaka5] but the level of more than hundred times higher densities may be impossible.
The enormous difficulties can be overcome by using a non-thermal ignition scheme[Reference Hora, Miley, Ghorannviss, Malekynia, Azizi and He6]. On top the recent measurement of several kilotesla magnetic fields[Reference Fujioka, Zhang, Ishihara, Shigemori, Hironaka, Johzaki, Sun ahara, Yamamoto, Nakashima, Watanabe, Shiraga, Nishimura and Azechi7] has to be involved but key ingredient on the way to a boron laser fusion reactor is the experimental discovery[Reference Picciotto, Margarone, Velyhan, Bellini, Krasa, Szydlowski, Bertuccio, Shi, Margarone, Prokupek, Malinowska, Krouski, Ullschmied, Laska, Kucharik and Korn8, Reference Labaune, Deprierraux, Goyon, Loisel, Yahia and Rafelski9] of the avalanche reaction of HB11[Reference Hora, Korn, Giuffrida, Margarone, Picciotto, Krasa, Jungwirth, Ullschmied, Lalousis, Eliezer, Miley, Moustaizis and Mourou1, Reference Lalousis, Hora and Moustaizis10] to open a radical new solution for fusion energy.
2 Non-thermal plasma block ignition of fusion
For the following new aspects with boron fusion it took dozens of years to realize the basic difference between the thermodynamic dominated laser fusion with nanosecond pulses in contrast to the entirely different non-thermal processes with the thousand times shorter picosecond laser–plasma interaction. The difference is given by the force density f in the plasma being not only determined by the gas dynamic pressure ![]() $p$ but also by the force
$p$ but also by the force ![]() $\mathbf{f}_{\text{NL}}$ due to electric E and magnetic B laser fields of frequency
$\mathbf{f}_{\text{NL}}$ due to electric E and magnetic B laser fields of frequency ![]() $\unicode[STIX]{x1D714}$,
$\unicode[STIX]{x1D714}$,
where the force ![]() $\mathbf{f}_{\text{NL}}$ is given by Maxwell’s stress tensor as Lorentz and gauge invariant nonlinear force determined by quadratic terms of fields (Ref. [Reference Hora11]: see Equation (8.88))
$\mathbf{f}_{\text{NL}}$ is given by Maxwell’s stress tensor as Lorentz and gauge invariant nonlinear force determined by quadratic terms of fields (Ref. [Reference Hora11]: see Equation (8.88))
 $$\begin{eqnarray}\displaystyle \mathbf{f}_{\text{NL}} & = & \displaystyle \unicode[STIX]{x1D6FB}\bullet [\mathbf{E}\mathbf{E}+\mathbf{H}\mathbf{H}-0.5(\mathbf{E}^{2}+\mathbf{H}^{2})\mathbf{1}\nonumber\\ \displaystyle & & \displaystyle +\,(1+(\unicode[STIX]{x2202}/\unicode[STIX]{x2202}t)/\unicode[STIX]{x1D714})(\mathbf{n}^{2}-1)\mathbf{E}\mathbf{E}]/(4\unicode[STIX]{x1D70B})\nonumber\\ \displaystyle & & \displaystyle -\,(\unicode[STIX]{x2202}/\unicode[STIX]{x2202}t)\mathbf{E}\times \mathbf{H}/(4\unicode[STIX]{x1D70B}c),\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \mathbf{f}_{\text{NL}} & = & \displaystyle \unicode[STIX]{x1D6FB}\bullet [\mathbf{E}\mathbf{E}+\mathbf{H}\mathbf{H}-0.5(\mathbf{E}^{2}+\mathbf{H}^{2})\mathbf{1}\nonumber\\ \displaystyle & & \displaystyle +\,(1+(\unicode[STIX]{x2202}/\unicode[STIX]{x2202}t)/\unicode[STIX]{x1D714})(\mathbf{n}^{2}-1)\mathbf{E}\mathbf{E}]/(4\unicode[STIX]{x1D70B})\nonumber\\ \displaystyle & & \displaystyle -\,(\unicode[STIX]{x2202}/\unicode[STIX]{x2202}t)\mathbf{E}\times \mathbf{H}/(4\unicode[STIX]{x1D70B}c),\end{eqnarray}$$ where 1 is the unity tensor and n is the complex optical constant of the plasma given by the plasma frequency ![]() $\unicode[STIX]{x1D714}_{p}$. At plane laser wave interaction with a plane plasma front, the nonlinear force reduces to
$\unicode[STIX]{x1D714}_{p}$. At plane laser wave interaction with a plane plasma front, the nonlinear force reduces to
showing how the force density is given by the negative gradient of the electromagnetic laser field energy density including the magnetic laser field from Maxwell’s equations. ![]() $E_{v}$ is the amplitude of the electric laser field in vacuum after time averaging. The second expression in Equation (4) is Kelvin’s formulation of the ponderomotive force in electrostatics of 1845.
$E_{v}$ is the amplitude of the electric laser field in vacuum after time averaging. The second expression in Equation (4) is Kelvin’s formulation of the ponderomotive force in electrostatics of 1845.
The difference to laser interaction by nanosecond thermal interaction against picosecond non-thermal nonlinear force driving is determined by ![]() $\mathbf{f}_{\text{NL}}$ interaction dominating in Equation (2). For the nanosecond interaction, the first term in Equation (2) dominates at low laser intensities while with picosecond, the second term can dominate in which case the laser intensity has to be high enough that the quiver energy of the electrons of the laser field is higher than their thermal energy of motion. A numerical example about nonlinear force acceleration of a slab of deuterium plasma irradiated by a neodymium glass laser pulse of
$\mathbf{f}_{\text{NL}}$ interaction dominating in Equation (2). For the nanosecond interaction, the first term in Equation (2) dominates at low laser intensities while with picosecond, the second term can dominate in which case the laser intensity has to be high enough that the quiver energy of the electrons of the laser field is higher than their thermal energy of motion. A numerical example about nonlinear force acceleration of a slab of deuterium plasma irradiated by a neodymium glass laser pulse of ![]() $10^{18}~\text{W}~\text{cm}^{-2}$ intensity is in Figure 1. During the 1.5 ps, the plasma reached velocities above
$10^{18}~\text{W}~\text{cm}^{-2}$ intensity is in Figure 1. During the 1.5 ps, the plasma reached velocities above ![]() $10^{9}~\text{cm}~\text{s}^{-1}$ showing the ultrahigh acceleration above
$10^{9}~\text{cm}~\text{s}^{-1}$ showing the ultrahigh acceleration above ![]() $10^{20}~\text{cm}~\text{s}^{-2}$. The generation of the plasma blocks, one moving against the laser light and the other into the higher density target is the result of a non-thermal collisionless absorption and should not be understood as radiation pressure acceleration but as a dielectric explosion driving the plasma blocks.
$10^{20}~\text{cm}~\text{s}^{-2}$. The generation of the plasma blocks, one moving against the laser light and the other into the higher density target is the result of a non-thermal collisionless absorption and should not be understood as radiation pressure acceleration but as a dielectric explosion driving the plasma blocks.

Figure 1. ![]() $10^{18}~\text{W}~\text{cm}^{-2}$ neodymium glass laser incident from the right-hand side on an initially 100 eV hot deuterium plasma slab whose initial density has a very low reflecting bi-Rayleigh profile, resulting in a laser energy density and a velocity distribution from plasma hydrodynamic computations at time
$10^{18}~\text{W}~\text{cm}^{-2}$ neodymium glass laser incident from the right-hand side on an initially 100 eV hot deuterium plasma slab whose initial density has a very low reflecting bi-Rayleigh profile, resulting in a laser energy density and a velocity distribution from plasma hydrodynamic computations at time ![]() $t=1.5~\text{ps}$ of interaction. The driving nonlinear force is the negative of the energy density gradient of the laser field
$t=1.5~\text{ps}$ of interaction. The driving nonlinear force is the negative of the energy density gradient of the laser field ![]() $(\mathbf{E}^{2}+\mathbf{H}^{2})/8\unicode[STIX]{x1D70B}$. The dynamic development of temperature and density had accelerated the plasma block of about 15 vacuum wave length thickness of the dielectric enlarged skin layer moving against the laser (positive velocity) and another block into the plasma (negative velocity) showing ultrahigh
$(\mathbf{E}^{2}+\mathbf{H}^{2})/8\unicode[STIX]{x1D70B}$. The dynamic development of temperature and density had accelerated the plasma block of about 15 vacuum wave length thickness of the dielectric enlarged skin layer moving against the laser (positive velocity) and another block into the plasma (negative velocity) showing ultrahigh ![]() ${>}10^{20}~\text{cm}~\text{s}^{-2}$ acceleration (Ref. [Reference Hora12]: Figures 10.18a&b) as computer result of 1978.
${>}10^{20}~\text{cm}~\text{s}^{-2}$ acceleration (Ref. [Reference Hora12]: Figures 10.18a&b) as computer result of 1978.
The experimental proof of the ultrahigh acceleration was possible[Reference Sauerbrey13] in full agreement with the results of computations in 1978 with domination by the nonlinear force, when laser pulses of higher than terawatt power and about ps duration were available after discovering the chirped pulse amplification (CPA)[Reference Stickland and Mourou14, Reference C. P. J, Key, Britten, Beach, Beer, Brown, Bryan, Caird, Carlson, Crane, Dawson, Erlandson, Fittinghoff, Hermann, Hoaglan, Iyer, Jones, Jovanovic, Komashko, Landen, Liao, Molander, Mitchell, Moses, Nielsen, Nguyen, Nissen, Payne, Pennington, Risinger, Rushford, Skulina, Spaeth, Stuart, Tietbohl and Wattellier15]. With these picosecond ultrahigh accelerations, the plasma block ignition of solid density DT by the nonlinear force was possible and updated[Reference Hora16]. Computation of DT fusion using the ps-block ignition[Reference Lalousis, Hora, Eliezer, Martinez-Val, Moustaizis, Miley and Mourou17] showed many details of the generated fusion flames with velocities of few ![]() $1000~\text{km}~\text{s}^{-1}$, the delayed generation of a Rankine–Hugoniot shock front, local distribution of reaction rates, etc., however, only in one-dimensional plane wave computations.
$1000~\text{km}~\text{s}^{-1}$, the delayed generation of a Rankine–Hugoniot shock front, local distribution of reaction rates, etc., however, only in one-dimensional plane wave computations.
To summarize, what is experimentally and theoretically clarified is the ultrahigh acceleration of plasma blocks measured by Sauerbrey[Reference Sauerbrey13], repeated by Földes et al. [Reference Földes, Bakos, Gal, Juhasz, Kedves, Koscis, Szatmari and Veres18], and measured by Badziak et al. [Reference Badziak, Makowski, Paris, Ryc, Wolowski, Woryna, Kozlov and Vankov19] as skin layer plasma block moving against the laser light all in exact agreement with the numerical prediction (Figure 1) based on non-thermal nonlinear force processes[Reference Hora, Badziak, Read, Li, Liang, Liu, Shang, Zhang, Osman, Miley, Zhang, He, Peng, Glowacz, Jablonski, Wolowski, Skladanowski, Jungwirth, Rohlena and Ullschmied20–Reference Hora22] as dielectric explosion. The necessary conditions are unique: providing a flat interaction surface, avoiding self-focusing, and providing an extremely high contrast of the laser pulse. The exclusion of relativistic self-focusing was measured in a most exceptional way by Zhang et al. [Reference Zhang, He, Chen, Li, Zhang, Wong, Feng, Zhang, Tang and Zhang23] in contrast to the very broad stream of measurements where always very intense and hard x-ray emission was measured. The conditions of flat interaction and extremely high contrast arrived at low intensity soft x-ray emission with the discovery that this was due to the elimination of self-focusing as the key condition for the experiments[Reference Sauerbrey13, Reference Földes, Bakos, Gal, Juhasz, Kedves, Koscis, Szatmari and Veres18, Reference Badziak, Makowski, Paris, Ryc, Wolowski, Woryna, Kozlov and Vankov19]. This is a perfect solidification of the picosecond nonlinear force non-thermal block acceleration process.
The broad stream of experiments did not fulfill these conditions beginning with the use of not sufficiently clean laser pulses[Reference Teubner, Uschmann, Gibbon, Altenbernd, Förster, Feurer, Sauerbrey, Hirst, Key, Lister and Neely24] and most of the phenomena reported from numerous experiments with not fulfilling the conditions e.g., Ref. [Reference Yang, Miley, Flippo and Hora25]. For the following studies it is important to measure the variations of the conditions to re-establish what is needed for using the fulfilled conditions of the successful experiments[Reference Sauerbrey13, Reference Földes, Bakos, Gal, Juhasz, Kedves, Koscis, Szatmari and Veres18, Reference Badziak, Makowski, Paris, Ryc, Wolowski, Woryna, Kozlov and Vankov19, Reference Zhang, He, Chen, Li, Zhang, Wong, Feng, Zhang, Tang and Zhang23]. After realizing this knowledge the very diversifying acceleration mechanisms can be categorized experimentally as shown in recent examples[Reference Neely26–Reference Hegelich28].
For the theoretical–numerical understanding it should be noticed how extensive particles-in-cell (PIC) computations[Reference Gaillard, Kluge, Flippo, Bussmann, Gall, Lockard, Geissel, Offermann, Schollmeier, Sentoku and Cowan29] arrived at the same acceleration of plasma blocks in the 70 MJ ion energy range as by hydrodynamic computations[Reference Banati, Hora, Lalousis and Moustaizis30, Reference Hora and Banati31].
3 Radical change for boron fusion
The use of the confirmed ultrahigh acceleration of plasma blocks for igniting a fusion reaction[Reference Hora16, Reference Lalousis, Hora, Eliezer, Martinez-Val, Moustaizis, Miley and Mourou17] was based on the computational work of Chu[Reference Chu32] and of Bobin[Reference Bobin33]. For initiating the ignition of a solid density DT target by a plane geometry laser pulse, it was numerically evaluated that the laser pulse had to be short in the range of 1 ps and the energy flux density ![]() $E^{\ast }$ had to be above the threshold
$E^{\ast }$ had to be above the threshold ![]() ${E_{o}}^{\ast }$
${E_{o}}^{\ast }$
These conditions were far beyond the lasers of that time. This was the main reason to work with laser pulses of nanosecond duration and to use the thermal processes of ablation, compression, and thermonuclear ignition for generating fusion power. These conditions changed with the discovery of CPA[Reference Stickland and Mourou14, Reference C. P. J, Key, Britten, Beach, Beer, Brown, Bryan, Caird, Carlson, Crane, Dawson, Erlandson, Fittinghoff, Hermann, Hoaglan, Iyer, Jones, Jovanovic, Komashko, Landen, Liao, Molander, Mitchell, Moses, Nielsen, Nguyen, Nissen, Payne, Pennington, Risinger, Rushford, Skulina, Spaeth, Stuart, Tietbohl and Wattellier15] and the updating of the computations of the fusion reactions based on the same hydrodynamic conditions as[Reference Chu32] arrived at the same result of Equation (5) for DT fusion[Reference Hora, Malekynia, Ghoranneviss, Miley and He34]. Updating by using collective effects and inhibition of thermal conductivity at inhomogeneous plasmas resulted in a reduction of the threshold ![]() ${E_{\text{o}}}^{\ast }$ to lower values up to a factor 20[Reference Hora, Malekynia, Ghoranneviss, Miley and He34]. These results were confirmed[Reference Földes, Bakos, Gal, Juhasz, Kedves, Koscis, Szatmari and Veres18] with deriving a number of further details by using a basically different genuine multi-fluid hydrodynamic code[Reference Lalousis and Hora35, Reference Hora, Lalousis and Eliezer36].
${E_{\text{o}}}^{\ast }$ to lower values up to a factor 20[Reference Hora, Malekynia, Ghoranneviss, Miley and He34]. These results were confirmed[Reference Földes, Bakos, Gal, Juhasz, Kedves, Koscis, Szatmari and Veres18] with deriving a number of further details by using a basically different genuine multi-fluid hydrodynamic code[Reference Lalousis and Hora35, Reference Hora, Lalousis and Eliezer36].
Irradiating the picosecond pulses on solid density DT fuel for initiating a fusion reaction in plane geometry[Reference Chu32] needed a threshold for the energy flux density of ![]() $E^{\ast }=5\times 10^{8}~\text{J}~\text{cm}^{-2}$, Equation (5). This non-thermal picosecond ignition of fusion as described in the preceding section, was exactly reproduced by a similar one fluid computation, where however later discovered plasma properties as the inhibition factor and the collective collisions had to be included and led to the updating for DT[Reference Bobin33]. When instead of the DT cross-sections, those for the much more difficult case for HB11 were used, in the same computations, a most unexpected and surprising result was achieved. Instead of the earlier known extremely more difficult ignition compared with DT, the threshold
$E^{\ast }=5\times 10^{8}~\text{J}~\text{cm}^{-2}$, Equation (5). This non-thermal picosecond ignition of fusion as described in the preceding section, was exactly reproduced by a similar one fluid computation, where however later discovered plasma properties as the inhibition factor and the collective collisions had to be included and led to the updating for DT[Reference Bobin33]. When instead of the DT cross-sections, those for the much more difficult case for HB11 were used, in the same computations, a most unexpected and surprising result was achieved. Instead of the earlier known extremely more difficult ignition compared with DT, the threshold ![]() $E^{\ast }$ for HB11 was of nearly the same value[Reference Hora, Miley, Ghorannviss, Malekynia, Azizi and He6, Reference Hora16, Reference Hora, Miley, Ghoranneviss, Malekynia and Azizi37]. This can be seen in Figure 2 where in the same way as calculated before by Chu[Reference Chu32], the maximum temperature of the reacting plasma depending on the time
$E^{\ast }$ for HB11 was of nearly the same value[Reference Hora, Miley, Ghorannviss, Malekynia, Azizi and He6, Reference Hora16, Reference Hora, Miley, Ghoranneviss, Malekynia and Azizi37]. This can be seen in Figure 2 where in the same way as calculated before by Chu[Reference Chu32], the maximum temperature of the reacting plasma depending on the time ![]() $t$ after the ps long initiation process was calculated.
$t$ after the ps long initiation process was calculated.

Figure 2. The picosecond laser pulse initiation of fusion flame in solid density HB11: maximum temperature of fusion reaction at time after initiation showing ignition at laser energy flux of ![]() $8\times 10^{8}~\text{J}~\text{cm}^{-2}$[Reference Hora, Miley, Ghorannviss, Malekynia, Azizi and He6].
$8\times 10^{8}~\text{J}~\text{cm}^{-2}$[Reference Hora, Miley, Ghorannviss, Malekynia, Azizi and He6].
In difference to the computations with the single fluid hydrodynamics[Reference Hora, Miley, Ghorannviss, Malekynia, Azizi and He6, Reference Hora16, Reference Hora, Malekynia, Ghoranneviss, Miley and He34, Reference Hora, Miley, Ghoranneviss, Malekynia and Azizi37], when performing the computations with the much more detailed genuine two-fluid hydrodynamics[Reference Lalousis and Hora35, Reference Hora, Lalousis and Eliezer36], the properties of the Rankine–Hugoniot shock generation were reproduced for HB11 in a more general way showing the plasma collision generated broadening of the shock front, the very high internal electric fields and their decay, and their delayed built-up within hundreds of picoseconds after the picosecond laser pulse initiation[Reference Lalousis, Hora, Eliezer, Martinez-Val, Moustaizis, Miley and Mourou17].
The difference between DT and HB11 was the reaction temperature, which was as expected above the threshold with respect to losses by bremsstrahlung emission above the limiting temperatures of 4 keV for DT and 65 keV for HB11. This was automatically included since the initial computations by Chu[Reference Chu32].
4 Cylindrical plasma trapping by ultrahigh laser generated magnetic fields
Despite of the attention given to the result[Reference Hora, Miley, Ghorannviss, Malekynia, Azizi and He6, Reference Hora, Miley, Ghoranneviss, Malekynia and Azizi37] by finding the nonlinear force conditions for abolishing the difference of laser fusion between HB11 and DT, this result was limited to cases of plane geometry. In reality the laser pulses are not infinitely spread by beams and the radial losses at target interaction and radiation emission have to be taken into account. The first step was to use spherical geometry. In this case, the computations profit from a compression of the initially solid-state fusion fuel. The chirped pulse amplification for picosecond laser pulses up to exawatt power can be considered possible in further future[Reference Hora16, Reference Hora, Lalousis and Moustaizis38]. However with these pulses, the gains both for DT or for HB can be only up to the range of few hundreds with exawatt laser pulses. And this is too low though 200-PW-picosecond laser pulses are available next[Reference Barty39].
A way other than spherical geometry was possible with cylindrical geometry after the discovery of Fujioka et al. [Reference Fujioka, Zhang, Ishihara, Shigemori, Hironaka, Johzaki, Sun ahara, Yamamoto, Nakashima, Watanabe, Shiraga, Nishimura and Azechi7] to generate magnetic fields of 4.5 kT by laser interaction shown in Figure 3. Hydrodynamic computations demonstrate how a cylindrical fusion plasma in solid-state density of HB11 coaxially located within the coils in Figure 3 can be trapped within the volume of few cubic millimeters with a magnetic field of 10 kT. The fusion reactions for HB11 show ignition by using binary reactions during few nanoseconds of the presence of the ultrahigh magnetic field from the generated fluid of alpha particles being in a similar way trapped and cylindrically confined using then the genuine two-fluid plasma hydrodynamics[Reference Lalousis, Hora and Moustaizis10, Reference Lalousis, Hora, Eliezer, Martinez-Val, Moustaizis, Miley and Mourou17, Reference Lalousis and Hora35, Reference Hora, Lalousis and Eliezer36, Reference Hora, Lalousis and Moustaizis38].

Figure 3. Generation of a 4.5 kT magnetic field within the coils of about 2 ns duration in the coils by firing a ![]() ${>}$ kilojoule nanosecond laser pulse 1 into the hole between the plates[Reference Fujioka, Zhang, Ishihara, Shigemori, Hironaka, Johzaki, Sun ahara, Yamamoto, Nakashima, Watanabe, Shiraga, Nishimura and Azechi7].
${>}$ kilojoule nanosecond laser pulse 1 into the hole between the plates[Reference Fujioka, Zhang, Ishihara, Shigemori, Hironaka, Johzaki, Sun ahara, Yamamoto, Nakashima, Watanabe, Shiraga, Nishimura and Azechi7].

Figure 4. Alpha density ![]() $N_{a}$ depending on the radius
$N_{a}$ depending on the radius ![]() $r$ at different times (from lowest to highest curves for 100, 500 and 1000 ps, respectively) showing ignition from the increase of the curves on time calculated for irradiating a cm long solid HB11 cylinder of 0.2 mm diameter with a picosecond laser pulse of 30 PW for plasma block initiation of the fusion reaction[Reference Lalousis, Hora and Moustaizis10].
$r$ at different times (from lowest to highest curves for 100, 500 and 1000 ps, respectively) showing ignition from the increase of the curves on time calculated for irradiating a cm long solid HB11 cylinder of 0.2 mm diameter with a picosecond laser pulse of 30 PW for plasma block initiation of the fusion reaction[Reference Lalousis, Hora and Moustaizis10].
Extensive hydrodynamic computations for 10 kT magnetic trapping in support of the results in Ref. [Reference Lalousis, Hora and Moustaizis10] are collected in Ref. [Reference Hora40] as figures, where 10.13 to 10.23 for laser pulses of picosecond duration and ![]() $10^{20}~\text{W}~\text{cm}^{-2}$ for laser intensity by block ignition as described in the preceding section. The cylindrical trapping of the laser pulse within the coils and their very slow radial expansion against the magnetic field of 10 kT was shown in very detailed calculations, e.g., if the coaxially located solid HB11 target was of 1 cm length and 1 mm radius.
$10^{20}~\text{W}~\text{cm}^{-2}$ for laser intensity by block ignition as described in the preceding section. The cylindrical trapping of the laser pulse within the coils and their very slow radial expansion against the magnetic field of 10 kT was shown in very detailed calculations, e.g., if the coaxially located solid HB11 target was of 1 cm length and 1 mm radius.
Complete trapping beyond nanosecond reaction time was confirmed while the propagation of the reaction front parallel to the magnetic field was of few thousand ![]() $\text{km}~\text{s}^{-1}$ and was well comparable to cases with DT fusion at the same fusion scheme. For testing the radial trapping by the ultrahigh magnetic fields[Reference Fujioka, Zhang, Ishihara, Shigemori, Hironaka, Johzaki, Sun ahara, Yamamoto, Nakashima, Watanabe, Shiraga, Nishimura and Azechi7], an even thinner fuel cylinder of 0.2 mm was used[Reference Lalousis, Hora and Moustaizis10]. Then a slow expansion of the alpha particle fluid – well at more than 100 times lower density than the solid-state fuel – is shown for different times after the picosecond plasma block ignition with a 30 PW laser pulse in Figure 4[Reference Lalousis, Hora and Moustaizis10]. Block ignition of an HB11 fusion fuel cylinder of 1 mm radius in the axis of the coil by a picosecond laser pulse 2 needs powers above exawatt for gains in the range of 300. This is a next step of developing highest power laser pulses[Reference Barty39].
$\text{km}~\text{s}^{-1}$ and was well comparable to cases with DT fusion at the same fusion scheme. For testing the radial trapping by the ultrahigh magnetic fields[Reference Fujioka, Zhang, Ishihara, Shigemori, Hironaka, Johzaki, Sun ahara, Yamamoto, Nakashima, Watanabe, Shiraga, Nishimura and Azechi7], an even thinner fuel cylinder of 0.2 mm was used[Reference Lalousis, Hora and Moustaizis10]. Then a slow expansion of the alpha particle fluid – well at more than 100 times lower density than the solid-state fuel – is shown for different times after the picosecond plasma block ignition with a 30 PW laser pulse in Figure 4[Reference Lalousis, Hora and Moustaizis10]. Block ignition of an HB11 fusion fuel cylinder of 1 mm radius in the axis of the coil by a picosecond laser pulse 2 needs powers above exawatt for gains in the range of 300. This is a next step of developing highest power laser pulses[Reference Barty39].
5 Breakthrough based on HB11 avalanche reactions after measuring elevated fusion gains
All hydrodynamic computations reported up to this stage were using only binary reactions for HB11 fusion in the same way as given for DT. Higher reaction gains were in difference to DT considered by the fact that the generated alpha particles with energies of 2.9 MeV from HB11 can transfer energies around 600 keV to boron nuclei by elastic collisions. As it is well known as an anomaly compared with all fusion reactions, the fusion cross-section for HB11 is about ten times higher for HB11 at 600 keV center-of-mass energy, resulting in a secondary reaction with protons producing three new alphas with a subsequent possibility of an avalanche reaction. Discussions were documented since the 2012 IAEA fusion conference[Reference Hora, Lalousis, Moustaizis, Földes, Miley, Yang, He, Eliezer and Martinez-Val41] and were used as preliminary estimations[Reference Lalousis, Hora and Moustaizis10] on which an international patent application was based.
Measurements of alpha particles from HB11 reactions at irradiation with picosecond laser pulses were reported first[Reference Belyaev, Matafonov, Vinogradov, Krainov, Lisitsa, Roussetski, Ignatyev and Andrianov42] at numbers of about 1000, just above the detection threshold. More than one million alpha particles were detected in an experiment[Reference Labaune, Deprierraux, Goyon, Loisel, Yahia and Rafelski9] using a combination of laser driven ion acceleration and direct laser interaction with picosecond pulses. About billion alpha particles were measured at straight forward irradiation by pulses of about 100 ps duration and 500 J energy from the iodine Prague Asterix Laser System (PALS) laser[Reference Picciotto, Margarone, Velyhan, Bellini, Krasa, Szydlowski, Bertuccio, Shi, Margarone, Prokupek, Malinowska, Krouski, Ullschmied, Laska, Kucharik and Korn8] when using a most exotic target. This can be found in silicon crystals where about 10% boron was incorporated. Substituting extremely low boron concentrations within the lattice of silicon for p-conductivity was the key process for producing high ultrahigh frequency diodes[Reference Rebentisch43] and later for the crucial discovery of the polar transistor[Reference Shockly44]. A laser irradiation may be mentioned how an anomalous photoemission could be measured of these semiconductors producing electric double layers by surface traps[Reference Boreham, Newman, Höpfl and Hora45] including boron doped silicon. The interest in semiconductor physics for transistor effects was studying higher and higher boron concentrations up to densities with states of degenerate holes for p-conducting.
Just this extremely high boron doping for studying semiconducting properties of silicon led to the combination for laser-fusion experiments at PALS[Reference Picciotto, Margarone, Velyhan, Bellini, Krasa, Szydlowski, Bertuccio, Shi, Margarone, Prokupek, Malinowska, Krouski, Ullschmied, Laska, Kucharik and Korn8] with the most surprising measurement of the billion fusion reactions. These reaction gains were of extremely elevated values. Initially, these results were not referring to the relation of an avalanche reaction process[Reference Picciotto, Margarone, Velyhan, Bellini, Krasa, Szydlowski, Bertuccio, Shi, Margarone, Prokupek, Malinowska, Krouski, Ullschmied, Laska, Kucharik and Korn8]. However when these experiments[Reference Korn, Margarone and Picciotto46, Reference Labaune, Baccou, Yahla, Neuville and Rafelski.47] were evaluated as a result of several orders of magnitudes higher than expected from binary reactions – up to gains even higher than from DT by using reasonable comparisons – it was then evident, that there was the avalanche reaction happening[Reference Hora, Korn, Giuffrida, Margarone, Picciotto, Krasa, Jungwirth, Ullschmied, Lalousis, Eliezer, Miley, Moustaizis and Mourou1].
This proof of the avalanche process could then be taken as a reality for the anticipated evaluation[Reference Lalousis, Hora and Moustaizis10] of very high reaction gains to be used for the ![]() ${>}$ PW-ps laser pulse plasma block generation for initiation of the non-thermal ignition of the HB11 reactions in the cylindrical volumes of solid density fusion fuel at trapping by the ultrahigh 10 kT magnetic fields described in the preceding section. The generation of more than gigajoule energy of alpha particles by irradiating 30 kJ laser pulses can then be a way for designing a power reactor. The process during about one nanosecond within a volume of few cubic millimeters gives evidence that this can be used only for a controlled reaction for generating electricity.
${>}$ PW-ps laser pulse plasma block generation for initiation of the non-thermal ignition of the HB11 reactions in the cylindrical volumes of solid density fusion fuel at trapping by the ultrahigh 10 kT magnetic fields described in the preceding section. The generation of more than gigajoule energy of alpha particles by irradiating 30 kJ laser pulses can then be a way for designing a power reactor. The process during about one nanosecond within a volume of few cubic millimeters gives evidence that this can be used only for a controlled reaction for generating electricity.
The avalanche process can be explained on the elastic central collision where an initially resting 11B or proton nucleus of mass ![]() $m_{2}$ gains energy from the energy
$m_{2}$ gains energy from the energy ![]() $E_{\unicode[STIX]{x1D6FC}}$ of an alpha particle of mass
$E_{\unicode[STIX]{x1D6FC}}$ of an alpha particle of mass ![]() $m_{1}$. After an alpha with an energy
$m_{1}$. After an alpha with an energy ![]() $E_{\unicode[STIX]{x1D6FC}}=2900~\text{keV}$ has its second collision with a proton and this proton collides with a boron11, one gets an energy in their center-of-mass system of reference and energy
$E_{\unicode[STIX]{x1D6FC}}=2900~\text{keV}$ has its second collision with a proton and this proton collides with a boron11, one gets an energy in their center-of-mass system of reference and energy ![]() $E_{\text{cm}}(pB^{11})$[Reference Nevins and Swain48, Reference Eliezer, Hora, Korn, Nissim and Martinez-Val49], Figure 5.
$E_{\text{cm}}(pB^{11})$[Reference Nevins and Swain48, Reference Eliezer, Hora, Korn, Nissim and Martinez-Val49], Figure 5.

Figure 5. The proton–boron 11 fusion cross-section ![]() $\unicode[STIX]{x1D70E}$ recalculated from Nevins and Swain[Reference Nevins and Swain48, Reference Eliezer, Hora, Korn, Nissim and Martinez-Val49].
$\unicode[STIX]{x1D70E}$ recalculated from Nevins and Swain[Reference Nevins and Swain48, Reference Eliezer, Hora, Korn, Nissim and Martinez-Val49].
This energy is within the maximum cross-section ![]() $\unicode[STIX]{x1D70E}_{\text{max}}$ of HB11[Reference Nevins and Swain48, Reference Eliezer, Hora, Korn, Nissim and Martinez-Val49] as is shown in Figure 5. We get the energy for
$\unicode[STIX]{x1D70E}_{\text{max}}$ of HB11[Reference Nevins and Swain48, Reference Eliezer, Hora, Korn, Nissim and Martinez-Val49] as is shown in Figure 5. We get the energy for ![]() $\text{HB}^{11}$ maximum cross-section
$\text{HB}^{11}$ maximum cross-section ![]() $\unicode[STIX]{x1D70E}$ from the alpha’s collisions with protons (that then collides with
$\unicode[STIX]{x1D70E}$ from the alpha’s collisions with protons (that then collides with ![]() $\text{B}^{11}$) to get the fusion, as the avalanche mechanism because of the multiplication through generation of three secondary alpha particles.
$\text{B}^{11}$) to get the fusion, as the avalanche mechanism because of the multiplication through generation of three secondary alpha particles.
In this process we get 2 classes of proton densities, ![]() $n_{p1}$ that did not have any alpha collision and
$n_{p1}$ that did not have any alpha collision and ![]() $n_{p2}$ that collided with alpha and got the right energy to have a proton–boron11 collision at maximum nuclear cross-section. It is conceivable to assume for this experiment[Reference Picciotto, Margarone, Velyhan, Bellini, Krasa, Szydlowski, Bertuccio, Shi, Margarone, Prokupek, Malinowska, Krouski, Ullschmied, Laska, Kucharik and Korn8]
$n_{p2}$ that collided with alpha and got the right energy to have a proton–boron11 collision at maximum nuclear cross-section. It is conceivable to assume for this experiment[Reference Picciotto, Margarone, Velyhan, Bellini, Krasa, Szydlowski, Bertuccio, Shi, Margarone, Prokupek, Malinowska, Krouski, Ullschmied, Laska, Kucharik and Korn8] ![]() $n_{p}=n_{p1}+n_{p2}$ and
$n_{p}=n_{p1}+n_{p2}$ and ![]() $n_{p1}\gg n_{p2}=n_{\unicode[STIX]{x1D6FC}}$ yielding the rate equation for the alpha particles
$n_{p1}\gg n_{p2}=n_{\unicode[STIX]{x1D6FC}}$ yielding the rate equation for the alpha particles
The second term is caused by the protons that collided with the alphas while the first term in this equation is caused by protons created in the laser–plasma interaction and are returned back into the target by the inverted double layer simulations[Reference Hora, Lalousis and Eliezer36]. Taking the data from the PALS experiment[Reference Picciotto, Margarone, Velyhan, Bellini, Krasa, Szydlowski, Bertuccio, Shi, Margarone, Prokupek, Malinowska, Krouski, Ullschmied, Laska, Kucharik and Korn8] Equation (7) can be solved numerically. In particular, the proton energy distribution as given in this experiment can be written as ![]() $\text{d}N_{p}/\text{d}E=N_{0}~[\text{MeV}^{-1}]$ for
$\text{d}N_{p}/\text{d}E=N_{0}~[\text{MeV}^{-1}]$ for ![]() $0<E<1$ MeV and
$0<E<1$ MeV and ![]() $\text{d}N_{p}/\text{d}E=0$ for
$\text{d}N_{p}/\text{d}E=0$ for ![]() $E>1$ MeV, where
$E>1$ MeV, where ![]() $N_{p}$ is the proton volume integrated density number and
$N_{p}$ is the proton volume integrated density number and ![]() $N_{0}=10^{11}$ is the total number of protons under consideration. This distribution implies
$N_{0}=10^{11}$ is the total number of protons under consideration. This distribution implies
 $$\begin{eqnarray}\begin{array}{@{}c@{}}\!\!\displaystyle \frac{\langle \unicode[STIX]{x1D70E}v\rangle }{\unicode[STIX]{x1D70E}_{\max }u}=\frac{\int _{0}^{\infty }f(E)\unicode[STIX]{x1D70E}(E)E^{1/2}\text{d}E/\int _{0}^{\infty }f(E)\text{d}E}{(1.2~\text{barn})\sqrt{0.6~\text{MeV}}}\approx 0.2,\\ \!\!\displaystyle f(E)=\left\{\begin{array}{@{}ll@{}}N_{0}=10^{11}~[\text{MeV}^{-1}] & \text{for}~0<E<1~\text{MeV}\\ 0 & \text{for}~1~\text{MeV}<E.\end{array}\right.\end{array}\end{eqnarray}$$
$$\begin{eqnarray}\begin{array}{@{}c@{}}\!\!\displaystyle \frac{\langle \unicode[STIX]{x1D70E}v\rangle }{\unicode[STIX]{x1D70E}_{\max }u}=\frac{\int _{0}^{\infty }f(E)\unicode[STIX]{x1D70E}(E)E^{1/2}\text{d}E/\int _{0}^{\infty }f(E)\text{d}E}{(1.2~\text{barn})\sqrt{0.6~\text{MeV}}}\approx 0.2,\\ \!\!\displaystyle f(E)=\left\{\begin{array}{@{}ll@{}}N_{0}=10^{11}~[\text{MeV}^{-1}] & \text{for}~0<E<1~\text{MeV}\\ 0 & \text{for}~1~\text{MeV}<E.\end{array}\right.\end{array}\end{eqnarray}$$Therefore to a good approximation we get the following solution
 $$\begin{eqnarray}\begin{array}{@{}l@{}}\displaystyle N_{\unicode[STIX]{x1D6FC}}=\frac{\langle \unicode[STIX]{x1D70E}v\rangle }{\unicode[STIX]{x1D70E}_{\max }u}N_{p}(\text{e}^{\unicode[STIX]{x1D70F}/\unicode[STIX]{x1D70F}_{A}}-1)\approx 0.2N_{0}\left(\frac{\unicode[STIX]{x1D70F}}{\unicode[STIX]{x1D70F}_{A}}\right),\\ \displaystyle \unicode[STIX]{x1D70F}_{A}\equiv \frac{1}{3n_{B}\unicode[STIX]{x1D70E}_{\max }u},\end{array}\end{eqnarray}$$
$$\begin{eqnarray}\begin{array}{@{}l@{}}\displaystyle N_{\unicode[STIX]{x1D6FC}}=\frac{\langle \unicode[STIX]{x1D70E}v\rangle }{\unicode[STIX]{x1D70E}_{\max }u}N_{p}(\text{e}^{\unicode[STIX]{x1D70F}/\unicode[STIX]{x1D70F}_{A}}-1)\approx 0.2N_{0}\left(\frac{\unicode[STIX]{x1D70F}}{\unicode[STIX]{x1D70F}_{A}}\right),\\ \displaystyle \unicode[STIX]{x1D70F}_{A}\equiv \frac{1}{3n_{B}\unicode[STIX]{x1D70E}_{\max }u},\end{array}\end{eqnarray}$$ where ![]() $N_{0}$ is of the order of few times
$N_{0}$ is of the order of few times ![]() $10^{11}$ and
$10^{11}$ and ![]() $N_{\unicode[STIX]{x1D6FC}}$ of the order of
$N_{\unicode[STIX]{x1D6FC}}$ of the order of ![]() $10^{9}$ are accordingly the volume integrated density numbers as given in the measurement[Reference Picciotto, Margarone, Velyhan, Bellini, Krasa, Szydlowski, Bertuccio, Shi, Margarone, Prokupek, Malinowska, Krouski, Ullschmied, Laska, Kucharik and Korn8].
$10^{9}$ are accordingly the volume integrated density numbers as given in the measurement[Reference Picciotto, Margarone, Velyhan, Bellini, Krasa, Szydlowski, Bertuccio, Shi, Margarone, Prokupek, Malinowska, Krouski, Ullschmied, Laska, Kucharik and Korn8]. ![]() $\unicode[STIX]{x1D70F}_{A}$ is defined as the avalanche time and the interaction time
$\unicode[STIX]{x1D70F}_{A}$ is defined as the avalanche time and the interaction time ![]() $\unicode[STIX]{x1D70F}$ to create alphas. In the Prague experiment
$\unicode[STIX]{x1D70F}$ to create alphas. In the Prague experiment ![]() $\unicode[STIX]{x1D70F}_{A}$ is of the order of 100 ns (
$\unicode[STIX]{x1D70F}_{A}$ is of the order of 100 ns (![]() $n_{B}=10^{22}~\text{cm}^{-3}$,
$n_{B}=10^{22}~\text{cm}^{-3}$, ![]() $\unicode[STIX]{x1D70E}_{\text{max}}=1.2$ barns and
$\unicode[STIX]{x1D70E}_{\text{max}}=1.2$ barns and ![]() $u=10^{9}~\text{cm}~\text{s}^{-1}$) which means that alphas are created during the range of 1 ns.
$u=10^{9}~\text{cm}~\text{s}^{-1}$) which means that alphas are created during the range of 1 ns.
The HB11 plasma contains then a component of the lower density of a fluid of alpha particles with the elastic collisions of boron nuclei at around 600 keV energy. This is a typical non-ideal plasma known from other applications[Reference Fortov, Iakubov and Bronstein50].
A completely different approach to study the avalanche reaction (alternatively called chain reaction)[Reference Labaune, Deprierraux, Goyon, Loisel, Yahia and Rafelski9, Reference Belyaev, Krainov, Matafonov and Zagreev51] uses the experiment of Refs. [Reference Labaune, Deprierraux, Goyon, Loisel, Yahia and Rafelski9, Reference Labaune, Baccou, Yahla, Neuville and Rafelski.47] but under more general conditions including natural boron containing also the isotope 10B. The side reaction of the alphas with 11B is to produce 14C resulting neutrons carrying ![]() $5\times 10^{-6}$ of the energy of the alphas of Equation (1).
$5\times 10^{-6}$ of the energy of the alphas of Equation (1).
6 Clean fusion power reactor
After the experimental confirmation[Reference Hora, Korn, Giuffrida, Margarone, Picciotto, Krasa, Jungwirth, Ullschmied, Lalousis, Eliezer, Miley, Moustaizis and Mourou1] of the avalanche ignition of the HB11 picosecond plasma block initiation of the fusion reaction with high gains at trapping by ultrahigh magnetic fields and the modeling of the avalanche process[Reference Eliezer, Hora, Korn, Nissim and Martinez-Val49], the result[Reference Lalousis, Hora and Moustaizis10] may be used for the concept how 30 kJ laser pulses of picosecond duration may produce more than 1 GJ energy from a solid density fuel cylinder. This is indeed subject to research about numerous further details of the reaction e.g., how instead of the assumed constant ultrahigh magnetic field, the temporal variations of the field have to be included.
Subject to clarify further details it is estimated how a power generator may be designed (Figure 6). The energy of the alpha particles can be converted with a gain above 90% electrostatically by their motion against a negative electric field (Figure 6) in the range of 1.4 MV. Heat generation is in the range of percents of the fusion energy. The mechanical shock of the alphas is reduced by the square root of the ratio of nuclear energy over chemical energy to negligible levels.

Figure 6. Scheme of an HB11 fusion reactor without radioactive radiation problems is based on non-thermal plasma block ignition by nonlinear forces (Section 2) by a 30-kJ-picosecond laser pulse 2 (Figure 2) where the solid hydrogen–boron fuel in the cylindrical axis of the magnetic coil is trapped by a 10 kT field sustained for about 1 ns after being generated by a nanosecond long laser pulse 1. The central reaction unit (Figure 3 in the center of the sphere) is electric charged to the level of ![]() $-1.4$ MV against the wall of a sphere producing alpha particles (helium nuclei) of more than a gigajoule energy, of which a small part is needed for the operation of the laser pulses. One part of the gained costs of electricity is needed for the apparatus of the central reaction and for the boron metal of the fuel being destroyed at each reaction[Reference Hora, Korn, Giuffrida, Margarone, Picciotto, Krasa, Jungwirth, Ullschmied, Lalousis, Eliezer, Miley, Moustaizis and Mourou1, Reference Lalousis, Hora and Moustaizis10, Reference Miley, Hora and Kirchhoff52, Reference Hora and Kirchhoff53].
$-1.4$ MV against the wall of a sphere producing alpha particles (helium nuclei) of more than a gigajoule energy, of which a small part is needed for the operation of the laser pulses. One part of the gained costs of electricity is needed for the apparatus of the central reaction and for the boron metal of the fuel being destroyed at each reaction[Reference Hora, Korn, Giuffrida, Margarone, Picciotto, Krasa, Jungwirth, Ullschmied, Lalousis, Eliezer, Miley, Moustaizis and Mourou1, Reference Lalousis, Hora and Moustaizis10, Reference Miley, Hora and Kirchhoff52, Reference Hora and Kirchhoff53].
The just reported HB11 fusion gain for producing alpha particle energy of more than GJ, equal to 277 kWh by the laser pulse 2 in Figure 3 of 30 kJ, permits in principle the scheme of an economic and absolute clean power reactor (Figure 6). For a power station, the main part of the generated energy of the alpha particles from the level of a ![]() $-1.4$ MV voltage, can be converted into[Reference Gotham and Heydt54] poly-phase alternating current as known from the megavolt-direct-current transmission line techniques described by Kanngiesser et al. [Reference Kanngiesser, Huang and Lips55] and Breuer et al. [Reference Breuer, Povh, Retzmann, Urbanke and Weinhold56]. If the reactor works with a frequency of one shot per second, the electric current for conversion is 714 A averaged between each fusion reaction. With this operation at 1 Hz, the reactor can produce estimated power of more than $300 Million per year covering operational costs and an attractive profit.
$-1.4$ MV voltage, can be converted into[Reference Gotham and Heydt54] poly-phase alternating current as known from the megavolt-direct-current transmission line techniques described by Kanngiesser et al. [Reference Kanngiesser, Huang and Lips55] and Breuer et al. [Reference Breuer, Povh, Retzmann, Urbanke and Weinhold56]. If the reactor works with a frequency of one shot per second, the electric current for conversion is 714 A averaged between each fusion reaction. With this operation at 1 Hz, the reactor can produce estimated power of more than $300 Million per year covering operational costs and an attractive profit.
7 Conclusions
A conclusion may be given with some remarks about next steps of activities. A possible ‘potential to the best route to fusion energy’[Reference Haan57] was drawn in Figure 6 which may refer to the here discussed combination of the
∙ reported anomaly of the very significant increase of the HB11 fusion gains[Reference Picciotto, Margarone, Velyhan, Bellini, Krasa, Szydlowski, Bertuccio, Shi, Margarone, Prokupek, Malinowska, Krouski, Ullschmied, Laska, Kucharik and Korn8, Reference Labaune, Deprierraux, Goyon, Loisel, Yahia and Rafelski9];
∙ with the measurement of ultrahigh magnetic fields[Reference Fujioka, Zhang, Ishihara, Shigemori, Hironaka, Johzaki, Sun ahara, Yamamoto, Nakashima, Watanabe, Shiraga, Nishimura and Azechi7];
∙ and with the picosecond initiated ultrahigh non-thermal plasma block acceleration by the dominance of the nonlinear (ponderomotive) force predicted (Figure 1)[Reference Hora12] and measured first by Sauerbrey[Reference Sauerbrey13].
The absolute rocklike confirmation of the last fact by the theoretical basis of the Maxwellian stress tensor and the experimental verification based on CPA[Reference Stickland and Mourou14] with the first picosecond laser pulses of 2 PW power[Reference C. P. J, Key, Britten, Beach, Beer, Brown, Bryan, Caird, Carlson, Crane, Dawson, Erlandson, Fittinghoff, Hermann, Hoaglan, Iyer, Jones, Jovanovic, Komashko, Landen, Liao, Molander, Mitchell, Moses, Nielsen, Nguyen, Nissen, Payne, Pennington, Risinger, Rushford, Skulina, Spaeth, Stuart, Tietbohl and Wattellier15, Reference Mourou, Barty and Perry58, Reference Cowan, Perry, Key, Dittmire, Hatchett, Henry, Moody, Moran, Pennington, Phillips, Sangster, Sefcik, Singh, Snavely, Stoyer, Wilks, Young, Takahashi, Dong, Fountain, Parnell, Johnson, Hunt and Kuhl59] needed a recognition in view of experimental facts from a flood of experiments about very different kinds of accelerations (including positron production and gamma rays for nuclear transmutations, etc.). It was a very rare clarification from a most exceptional observation of x-ray emission by Zhang et al. [Reference Zhang, He, Chen, Li, Zhang, Wong, Feng, Zhang, Tang and Zhang23] why the measurements of Sauerbrey[Reference Sauerbrey13] and later[Reference Földes, Bakos, Gal, Juhasz, Kedves, Koscis, Szatmari and Veres18, Reference Badziak, Makowski, Paris, Ryc, Wolowski, Woryna, Kozlov and Vankov19], etc. were so dramatically unique: one had to avoid relativistic self-focusing by using laser pulses of extreme contrast ratios. As a point of next research, these conditions for the plasma block generation (also for hadron cancer therapy[Reference Banati, Hora, Lalousis and Moustaizis30]) should explore the final limits of the conditions of the experiments first verified by Sauerbrey[Reference Sauerbrey13].
Another need for experimental exploration is the numerically very detailed picosecond initiation of the fusion reactions in solid density fuel by Chu and Bobin[Reference Chu32, Reference Bobin33] confirmed by alternative computation codes and conditions. As an experiment in this direction was the exceptionally high fusion gains measured by Norreys et al. [Reference Norreys, Fews, Beg, Bell, Dangor, Lee, Nelson, Schmidt, Tatarakis and Cable60] as discussed in connection to the present topic[Reference Hora22]. These experimental conditions were close to the irradiation of diamond foils of few nanometers thickness[Reference Steinke, Henig, Schnürer, Sokollik, Nickles, Jung, Kiefer, Hörlein, Schreiber, Tajima, Yan, Hegelich, Meyer-ter-Vehn, Sandner and Habs61] where the foils were not transparent above a thickness of 3% of the wave lengths with sub-picosecond laser pulses. There was no tunneling or other classical mechanism but a proof of the dielectric explosion by the nonlinear force[Reference Hora62].
Another point of exploration will be the detailed study of the cylindrical solid density fusion fuel in the axis of the coils with the 10 kT magnetic fields (Figure 3) to see at what field the ionization of the fuel will happen and at what time the best irradiation by the laser 2 should initiate the ignition. Another point of research will be the extraordinary increased HB11 fusion gains[Reference Picciotto, Margarone, Velyhan, Bellini, Krasa, Szydlowski, Bertuccio, Shi, Margarone, Prokupek, Malinowska, Krouski, Ullschmied, Laska, Kucharik and Korn8, Reference Labaune, Deprierraux, Goyon, Loisel, Yahia and Rafelski9, Reference Labaune, Baccou, Yahla, Neuville and Rafelski.47] as basis of the unique avalanche reaction. It should be mentioned that the expression ‘avalanche’ or ‘chain’ reaction was used first in the publications submitted in the same months[Reference Labaune, Deprierraux, Goyon, Loisel, Yahia and Rafelski9, Reference Hora, Lalousis and Moustaizis38]. Earlier, reference was given to ‘secondary reactions’[Reference Hora, Lalousis, Moustaizis, Földes, Miley, Yang, He, Eliezer and Martinez-Val41] until clarification was reached in documents with the German Patent office. The consideration of the avalanche process for the results of Ref. [Reference Picciotto, Margarone, Velyhan, Bellini, Krasa, Szydlowski, Bertuccio, Shi, Margarone, Prokupek, Malinowska, Krouski, Ullschmied, Laska, Kucharik and Korn8] was initiated later[Reference Korn, Margarone and Picciotto63] based on Ref. [Reference Lalousis, Hora and Moustaizis10] with reference to an IZEST conference[Reference Korn, Margarone and Picciotto46] leading to the result of Ref. [Reference Hora, Lalousis, Giuffrida, Margarone, Korn, Eliezer and Miley64]. Finally, the dramatic expansion of petawatt laser developments has to be motivated also for the aims of boron laser fusion[Reference Danson65, Reference Li, Liang, Gan, Lu, Yu, Yin, Leng, Lu, Wang and Xu66] beyond the steps to 200 PW pulses[Reference Barty39].