Hostname: page-component-8448b6f56d-dnltx Total loading time: 0 Render date: 2024-04-24T16:56:36.226Z Has data issue: false hasContentIssue false
  • English
  • Français

BROOKS’ THEOREM FOR MEASURABLE COLORINGS

Part of: Set theory Ergodic theory Combinatorial probability Graph theory Locally compact groups and their algebras

Published online by Cambridge University Press:  24 June 2016

CLINTON T. CONLEY ,
ANDREW S. MARKS  and
ROBIN D. TUCKER-DROB
CLINTON T. CONLEY
Affiliation:
Department of Mathematical Sciences, Carnegie Mellon University, Pittsburgh, PA 15213, USA; clintonc@andrew.cmu.edu
ANDREW S. MARKS
Affiliation:
UCLA Mathematics, BOX 951555, Los Angeles, CA 90095-1555, USA; marks@math.ucla.edu
ROBIN D. TUCKER-DROB
Affiliation:
Texas A&M Department of Mathematics, Mailstop 3368, Texas A&M University, College Station, TX 77843-3368, USA; rtuckerd@math.tamu.edu

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We generalize Brooks’ theorem to show that if 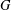$G$ is a Borel graph on a standard Borel space 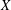$X$ of degree bounded by 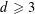$d\geqslant 3$ which contains no 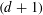$(d+1)$-cliques, then 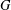$G$ admits a 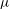${\it\mu}$-measurable 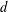$d$-coloring with respect to any Borel probability measure 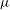${\it\mu}$ on 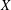$X$, and a Baire measurable 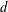$d$-coloring with respect to any compatible Polish topology on 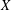$X$. The proof of this theorem uses a new technique for constructing one-ended spanning subforests of Borel graphs, as well as ideas from the study of list colorings. We apply the theorem to graphs arising from group actions to obtain factor of IID $d$-colorings of Cayley graphs of degree 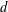$d$, except in two exceptional cases.

MSC classification

Primary: 03E15: Descriptive set theory 37A50: Relations with probability theory and stochastic processes 22D40: Ergodic theory on groups 60C05: Combinatorial probability 05C15: Coloring of graphs and hypergraphs
Type
Research Article
Information
Forum of Mathematics, Sigma , Volume 4 , 2016 , e16
Check for updates
Creative Commons
Creative Common License - CCCreative Common License - BY
This is an Open Access article, distributed under the terms of the Creative Commons Attribution licence (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted re-use, distribution, and reproduction in any medium, provided the original work is properly cited.
Copyright
© The Author(s) 2016

References

Aldous, D. and Lyons, R., ‘Processes on unimodular random networks’, Electron. J. Probab. 12 (2007), 1454–1508.CrossRefGoogle Scholar
Benjamini, I., Lyons, R., Peres, Y. and Schramm, O., ‘Critical percolation on any nonamenable group has no infinite clusters’, Ann. Probab. 27(3) (1999), 1347–1356.CrossRefGoogle Scholar
Benjamini, I., Lyons, R., Peres, Y. and Schramm, O., ‘Uniform spanning forests’, Ann. Probab. 29(1) (2001), 1–65.CrossRefGoogle Scholar
Borodin, O. V., ‘Criterion of chromaticity of a degree prescription (in Russian)’, inAbstracts of IV All-Union Conference on Theoretical Cybernetics (Novosibirsk) (1977), 127–128.Google Scholar
Conley, C. T. and Kechris, A. S., ‘Measurable chromatic and independence numbers for ergodic graphs and group actions’, Groups Geom. Dyn. 7(1) (2013), 127–180.Google Scholar
Conley, C. T., Kechris, A. S. and Tucker-Drob, R. D., ‘Ultraproducts of measure preserving actions and graph combinatorics’, Ergod. Th. & Dynam. Sys. 33(2) (2013), 334–374.CrossRefGoogle Scholar
Conley, C. T. and Miller, B. D., ‘A bound on measurable chromatic numbers of locally finite Borel graphs’, Math. Res. Lett., to appear.Google Scholar
Cranston, D. W. and Rabern, L., ‘Brooks’ theorem and beyond’, J. Graph Theory 80(3) (2014), doi:10.1002/jgt.21847.Google Scholar
Diestel, R., Graph Theory, Graduate Texts in Mathematics, 173 (Springer, Berlin, 2005).Google Scholar
Erdős, P., Rubin, A. and Taylor, H., ‘Choosability in graphs’, inProceedings of West Coast Conference on Combinatorics, Graph Theory and Computing (Humboldt State Univ., Arcata, Calif., 1979), Congressus Numerantium, 26 (1979), 125–157.Google Scholar
Gaboriau, D. and Lyons, R., ‘A measurable-group-theoretic solution to von Neumann’s problem’, Invent. Math. 177(3) (2009), 533–540.Google Scholar
Hjorth, G. and Miller, B. D., ‘Ends of graphed equivalence relations II’, Israel J. Math. 169(3) (2009), 393–415.CrossRefGoogle Scholar
Jackson, S., Kechris, A. S. and Louveau, A., ‘Countable Borel equivalence relations’, J. Math. Log. 2(1) (2002), 1–80.Google Scholar
Kechris, A. S., Classical Descriptive Set Theory, Graduate Texts in Mathematics, 156 (Springer, New York, 1995).CrossRefGoogle Scholar
Kechris, A. S. and Miller, B. D., Topics in Orbit Equivalence, Lecture Notes in Mathematics, 1852 (Springer, Berlin, 2004).CrossRefGoogle Scholar
Kechris, A. S., Solecki, S. and Todorcevic, S., ‘Borel chromatic numbers’, Adv. Math. 141(1) (1999), 1–44.Google Scholar
Lyons, R. and Nazarov, F., ‘Perfect matchings as IID factors on non-amenable groups’, European J. Combin. 32(7) (2011), 1115–1125.Google Scholar
Lyons, R., Peres, Y. and Schramm, O., ‘Minimal spanning forests’, Ann. Probab. 34(5) (2006), 1665–1692.Google Scholar
Marks, A., ‘A determinacy approach to Borel combinatorics’, J. Amer. Math. Soc. 29(2) (2016), 579–600.Google Scholar
Miller, B. D., ‘Ends of graphed equivalence relations I’, Israel J. Math. 169 (2009), 365–392.CrossRefGoogle Scholar
Miller, B. D., ‘The graph-theoretic approach to descriptive set theory’, Bull. Symbolic Logic (2012), 554–575.CrossRefGoogle Scholar
Pemantle, R., ‘Towards a theory of negative dependence’, J. Math. Phys. 41(3) (2002), 1371–1390.CrossRefGoogle Scholar
Zakrzewski, P., ‘On invariant ccc 𝜎-ideals on 2ℕ ’, Acta Math. Hungar. 143(2) (2014), 367–377.CrossRefGoogle Scholar