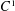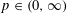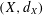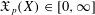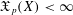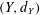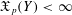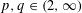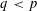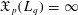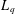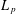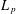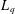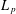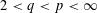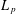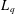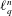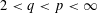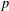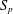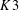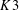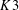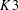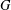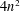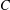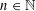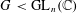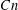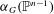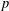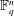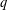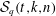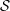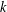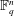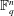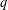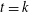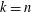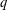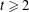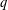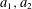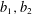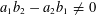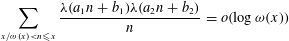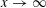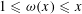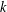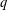Differential Geometry and Geometric Analysis
Research Article
AN ALTERNATE PROOF OF WISE’S MALNORMAL SPECIAL QUOTIENT THEOREM
- Part of:
-
- Published online by Cambridge University Press:
- 12 January 2016, e1
-
- Article
-
- You have access
- Open access
- Export citation
Differential Equations
Research Article
GLOBAL UNIQUENESS FOR THE CALDERÓN PROBLEM WITH LIPSCHITZ CONDUCTIVITIES
- Part of:
-
- Published online by Cambridge University Press:
- 13 January 2016, e2
-
- Article
-
- You have access
- Open access
- Export citation
Analysis
Research Article
METRIC
 $X_{p}$ INEQUALITIES
$X_{p}$ INEQUALITIES
- Part of:
-
- Published online by Cambridge University Press:
- 02 February 2016, e3
-
- Article
-
- You have access
- Open access
- Export citation
Mathematical Physics
Research Article
THE KATZ–KLEMM–VAFA CONJECTURE FOR
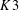 $K3$ SURFACES
$K3$ SURFACES
- Part of:
-
- Published online by Cambridge University Press:
- 06 June 2016, e4
-
- Article
-
- You have access
- Open access
- Export citation
Algebra
Research Article
THE
 ${\it\alpha}$-INVARIANT AND THOMPSON’S CONJECTURE
${\it\alpha}$-INVARIANT AND THOMPSON’S CONJECTURE
- Part of:
-
- Published online by Cambridge University Press:
- 08 July 2016, e5
-
- Article
-
- You have access
- Open access
- Export citation
Corrigendum
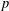 $p$-ADIC HODGE THEORY FOR RIGID-ANALYTIC VARIETIES – CORRIGENDUM
$p$-ADIC HODGE THEORY FOR RIGID-ANALYTIC VARIETIES – CORRIGENDUM
-
- Published online by Cambridge University Press:
- 12 August 2016, e6
-
- Article
-
- You have access
- Open access
- Export citation
Discrete Mathematics
Research Article
EXISTENCE OF
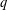 $q$-ANALOGS OF STEINER SYSTEMS
$q$-ANALOGS OF STEINER SYSTEMS
- Part of:
-
- Published online by Cambridge University Press:
- 30 August 2016, e7
-
- Article
-
- You have access
- Open access
- Export citation
Number Theory
Research Article
THE LOGARITHMICALLY AVERAGED CHOWLA AND ELLIOTT CONJECTURES FOR TWO-POINT CORRELATIONS
- Part of:
-
- Published online by Cambridge University Press:
- 27 September 2016, e8
-
- Article
-
- You have access
- Open access
- Export citation
Probability
Research Article
FINITELY DEPENDENT COLORING
- Part of:
-
- Published online by Cambridge University Press:
- 03 November 2016, e9
-
- Article
-
- You have access
- Open access
- Export citation