Skip to main content Accessibility help

We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.

Close cookie message
×
Home
  • Home
Hostname: page-component-684bc48f8b-4z9h4 Total loading time: 0.749 Render date: 2021-04-12T02:00:40.451Z Has data issue: true Feature Flags: { "shouldUseShareProductTool": true, "shouldUseHypothesis": true, "isUnsiloEnabled": true, "metricsAbstractViews": false, "figures": false, "newCiteModal": false, "newCitedByModal": true }
EnglishFrançais
Forum of Mathematics, Pi Forum of Mathematics, Pi

Article contents

MOMENTS OF RANDOM MULTIPLICATIVE FUNCTIONS, I: LOW MOMENTS, BETTER THAN SQUAREROOT CANCELLATION, AND CRITICAL MULTIPLICATIVE CHAOS

Part of: Probabilistic theory: distribution modulo $1$; metric theory of algorithms Stochastic processes Multiplicative number theory Exponential sums and character sums

Published online by Cambridge University Press:  20 January 2020

ADAM J. HARPER
ADAM J. HARPER
Affiliation:
Mathematics Institute, Zeeman Building, University of Warwick, CoventryCV4 7AL, England, UK; A.Harper@warwick.ac.uk
Corresponding
E-mail address:
A.Harper@warwick.ac.uk
Save pdf (0.5 mb)

Abstract

We determine the order of magnitude of 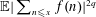$\mathbb{E}|\sum _{n\leqslant x}f(n)|^{2q}$, where 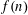$f(n)$ is a Steinhaus or Rademacher random multiplicative function, and 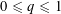$0\leqslant q\leqslant 1$. In the Steinhaus case, this is equivalent to determining the order of 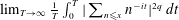$\lim _{T\rightarrow \infty }\frac{1}{T}\int _{0}^{T}|\sum _{n\leqslant x}n^{-it}|^{2q}\,dt$.

In particular, we find that 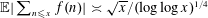$\mathbb{E}|\sum _{n\leqslant x}f(n)|\asymp \sqrt{x}/(\log \log x)^{1/4}$. This proves a conjecture of Helson that one should have better than squareroot cancellation in the first moment and disproves counter-conjectures of various other authors. We deduce some consequences for the distribution and large deviations of 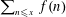$\sum _{n\leqslant x}f(n)$.

The proofs develop a connection between 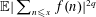$\mathbb{E}|\sum _{n\leqslant x}f(n)|^{2q}$ and the 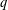$q$th moment of a critical, approximately Gaussian, multiplicative chaos and then establish the required estimates for that. We include some general introductory discussion about critical multiplicative chaos to help readers unfamiliar with that area.

MSC classification

Primary: 11N37: Asymptotic results on arithmetic functions
Secondary: 11L40: Estimates on character sums 11K65: Arithmetic functions 60G15: Gaussian processes 60G57: Random measures
Type
Number Theory
Information
Forum of Mathematics, Pi , Volume 8 , 2020 , e1
Check for updates
Creative Commons
Creative Common License - CCCreative Common License - BY
This is an Open Access article, distributed under the terms of the Creative Commons Attribution licence (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted re-use, distribution, and reproduction in any medium, provided the original work is properly cited.
Copyright
© The Author 2020

References

Arguin, L.-P., Belius, D. and Harper, A. J., ‘Maxima of a randomized Riemann zeta function, and branching random walks’, Ann. Appl. Probab. 27(1) (2017), 178–215.CrossRefGoogle Scholar
Barral, J., Kupiainen, A., Nikula, M., Saksman, E. and Webb, C., ‘Basic properties of critical lognormal multiplicative chaos’, Ann. Probab. 43(5) (2015), 2205–2249.CrossRefGoogle Scholar
Berestycki, N., ‘An elementary approach to Gaussian multiplicative chaos’, Electron. Commun. Probab. 22(Paper No. 27) (2017), 12 pp.CrossRefGoogle Scholar
Bondarenko, A. and Seip, K., ‘Helson’s problem for sums of a random multiplicative function’, Mathematika 62(1) (2016), 101–110.CrossRefGoogle Scholar
Chatterjee, S. and Soundararajan, K., ‘Random multiplicative functions in short intervals’, Int. Math. Res. Not. IMRN 2012 (2012), 479–492.CrossRefGoogle Scholar
Duplantier, B., Rhodes, R., Sheffield, S. and Vargas, V., ‘Renormalization of critical Gaussian multiplicative chaos and KPZ relation’, Comm. Math. Phys. 330(1) (2014), 283–330.CrossRefGoogle Scholar
Grimmett, G. R. and Stirzaker, D. R., Probability and Random Processes, 3rd edn, (Oxford University Press, New York, 2001).Google Scholar
Gut, A., Probability: A Graduate Course, 2nd edn, (Springer Texts in Statistics, New York, 2013).CrossRefGoogle Scholar
Halász, G., ‘On random multiplicative functions’, inHubert Delange Colloquium, (Orsay, 1982), Publications Mathématiques d’Orsay, 83 (Univ. Paris XI, Orsay, 1983), 74–96.Google Scholar
Harper, A. J., ‘Bounds on the suprema of Gaussian processes, and omega results for the sum of a random multiplicative function’, Ann. Appl. Probab. 23(2) (2013), 584–616.CrossRefGoogle Scholar
Harper, A. J., ‘On the limit distributions of some sums of a random multiplicative function’, J. reine angew. Math. 678 (2013), 95–124.Google Scholar
Harper, A. J., ‘Moments of random multiplicative functions, II: High moments’, Algebra Number Theory, to appear.Google Scholar
Harper, A. J., Nikeghbali, A. and Radziwiłł, M., ‘A note on Helson’s conjecture on moments of random multiplicative functions’, inAnalytic Number Theory (Springer, Cham, 2015), 145–169.CrossRefGoogle Scholar
Heap, W. and Lindqvist, S., ‘Moments of random multiplicative functions and truncated characteristic polynomials’, Q. J. Math. 67(4) (2016), 683–714.Google Scholar
Helson, H., ‘Hankel forms’, Studia Math. 198(1) (2010), 79–84.CrossRefGoogle Scholar
Hough, B., ‘Summation of a random multiplicative function on numbers having few prime factors’, Math. Proc. Cambridge Philos. Soc. 150 (2011), 193–214.CrossRefGoogle Scholar
Hu, Y. and Shi, Z., ‘Minimal position and critical martingale convergence in branching random walks, and directed polymers on disordered trees’, Ann. Probab. 37(2) (2009), 742–789.CrossRefGoogle Scholar
Lau, Y.-K., Tenenbaum, G. and Wu, J., ‘On mean values of random multiplicative functions’, Proc. Amer. Math. Soc. 141 (2013), 409–420. Also see www.iecl.univ-lorraine.fr/∼Gerald.Tenenbaum/PUBLIC/Prepublications_et_publications/RMF.pdf for some corrections to the published version.CrossRefGoogle Scholar
Lawler, G. F. and Limic, V., Random Walk: a Modern Introduction, 1st edn, (Cambridge University Press, Cambridge, 2010).CrossRefGoogle Scholar
Montgomery, H. L. and Vaughan, R. C., Multiplicative Number Theory I: Classical Theory, 1st edn, (Cambridge University Press, Cambridge, 2007).Google Scholar
Ng, N., ‘The distribution of the summatory function of the Möbius function’, Proc. Lond. Math. Soc. (3) 89(3) (2004), 361–389.CrossRefGoogle Scholar
Reinert, G. and Röllin, A., ‘Multivariate normal approximation with Stein’s method of exchangeable pairs under a general linearity condition’, Ann. Probab. 37(6) (2009), 2150–2173.CrossRefGoogle Scholar
Rhodes, R. and Vargas, V., ‘Gaussian multiplicative chaos and applications: A review’, Probab. Surv. 11 (2014), 315–392.CrossRefGoogle Scholar
Sadikova, S. M., ‘Two-dimensional analogues of an inequality of Esseen with applications to the Central Limit Theorem’, Theory Probab. Appl. 11 (1966), 325–335.CrossRefGoogle Scholar
Saksman, E. and Seip, K., ‘Integral means and boundary limits of Dirichlet series’, Bull. Lond. Math. Soc. 41(3) (2009), 411–422.CrossRefGoogle Scholar
Saksman, E. and Seip, K., ‘Some open questions in analysis for Dirichlet series’, inRecent Progress on Operator Theory and Approximation in Spaces of Analytic Functions, Contemp. Mathematics, 679 (American Mathematical Society, Providence, RI, 2016), 179–191.CrossRefGoogle Scholar
Saksman, E. and Webb, C., ‘Multiplicative chaos measures for a random model of the Riemann zeta function’, Preprint available online at http://arxiv.org/abs/1604.08378.Google Scholar
Saksman, E. and Webb, C., ‘The Riemann zeta function and Gaussian multiplicative chaos: statistics on the critical line’, Preprint available online at https://arxiv.org/abs/1609.00027.Google Scholar
Soundararajan, K., ‘Moments of the Riemann zeta function’, Ann. of Math. 170 (2009), 981–993.CrossRefGoogle Scholar
Weber, M. J. G., ‘L 1 -Norm of Steinhaus chaos on the polydisc’, Monatsh. Math. 181(2) (2016), 473–483.CrossRefGoogle Scholar
Wintner, A., ‘Random factorizations and Riemann’s hypothesis’, Duke Math. J. 11 (1944), 267–275.CrossRefGoogle Scholar

Full text views

Full text views reflects PDF downloads, PDFs sent to Google Drive, Dropbox and Kindle and HTML full text views.

Total number of HTML views: 0
Total number of PDF views: 831 *
View data table for this chart

* Views captured on Cambridge Core between 20th January 2020 - 12th April 2021. This data will be updated every 24 hours.

Access Access
Open access Open access
7
Cited by

Send article to Kindle

To send this article to your Kindle, first ensure no-reply@cambridge.org is added to your Approved Personal Document E-mail List under your Personal Document Settings on the Manage Your Content and Devices page of your Amazon account. Then enter the ‘name’ part of your Kindle email address below. Find out more about sending to your Kindle. Find out more about sending to your Kindle.

Note you can select to send to either the @free.kindle.com or @kindle.com variations. ‘@free.kindle.com’ emails are free but can only be sent to your device when it is connected to wi-fi. ‘@kindle.com’ emails can be delivered even when you are not connected to wi-fi, but note that service fees apply.

Find out more about the Kindle Personal Document Service.

MOMENTS OF RANDOM MULTIPLICATIVE FUNCTIONS, I: LOW MOMENTS, BETTER THAN SQUAREROOT CANCELLATION, AND CRITICAL MULTIPLICATIVE CHAOS
Available formats
×

Send article to Dropbox

To send this article to your Dropbox account, please select one or more formats and confirm that you agree to abide by our usage policies. If this is the first time you use this feature, you will be asked to authorise Cambridge Core to connect with your <service> account. Find out more about sending content to Dropbox.

MOMENTS OF RANDOM MULTIPLICATIVE FUNCTIONS, I: LOW MOMENTS, BETTER THAN SQUAREROOT CANCELLATION, AND CRITICAL MULTIPLICATIVE CHAOS
Available formats
×

Send article to Google Drive

To send this article to your Google Drive account, please select one or more formats and confirm that you agree to abide by our usage policies. If this is the first time you use this feature, you will be asked to authorise Cambridge Core to connect with your <service> account. Find out more about sending content to Google Drive.

MOMENTS OF RANDOM MULTIPLICATIVE FUNCTIONS, I: LOW MOMENTS, BETTER THAN SQUAREROOT CANCELLATION, AND CRITICAL MULTIPLICATIVE CHAOS
Available formats
×
×

Reply to: Submit a response

Your details

Conflicting interests

Do you have any conflicting interests? *