Hostname: page-component-7479d7b7d-q6k6v Total loading time: 0 Render date: 2024-07-10T19:57:15.094Z Has data issue: false hasContentIssue false
  • English
  • Français

Exact simulation for solutions of one-dimensional Stochastic Differential Equations with discontinuous drift

Published online by Cambridge University Press:  22 October 2014

Pierre Étoré  and
Miguel Martinez
Pierre Étoré
Affiliation:
ENSIMAG – Laboratoire Jean Kuntzmann, Tour IRMA 51, rue des Mathématiques, 38041 Grenoble cedex 9, France. pierre.etore@imag.fr
Miguel Martinez
Affiliation:
Université Paris-Est Marne-La-Vallée, Laboratoire d’Analyse et de Mathématiques Appliquées, UMR 8050, 5 Bld Descartes, Champs-sur-Marne, 77454 Marne-la-Vallée cedex 2, France; miguel.martinez@univ-mlv.fr
Get access

Abstract

In this note we propose an exact simulation algorithm for the solution of (1)

\begin{equation} \label{eds-intro} {\rm d}X_t={\rm d}W_t+\bar{b}(X_t){\rm d}t,\quad X_0=x, \end{equation}dXt=dWt+b̅(Xt)dt, X0=x,
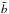where \hbox{$\bar{b}$}b̅ is a smooth real function except at point 0 where \hbox{$\bar{b}(0+)\neq \bar{b}(0-)$}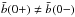b̅(0 + ) ≠ b̅(0 −). The main idea is to sample an exact skeleton of X using an algorithm deduced from the convergence of the solutions of the skew perturbed equation (2)
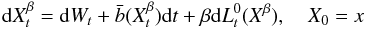\begin{equation} \label{edsbeta} {\rm d}X^\beta_t={\rm d}W_t+\bar{b}(X^\beta_t){\rm d}t + \beta {\rm d}L^0_t(X^\beta),\quad X_0=x \end{equation}dXtβ=dWt+b̅(Xtβ)dt+βdLt0(Xβ), X0=x
towards X solution of (1) as β ≠ 0 tends to 0. In this note, we show that this convergence induces the convergence of exact simulation algorithms proposed by the authors in [Pierre Étoré and Miguel Martinez. Monte Carlo Methods Appl. 19 (2013) 41–71] for the solutions of (2) towards a limit algorithm. Thanks to stability properties of the rejection procedures involved as β tends to 0, we prove that this limit algorithm is an exact simulation algorithm for the solution of the limit equation (1). Numerical examples are shown to illustrate the performance of this exact simulation algorithm.

Keywords

Exact simulation methodsBrownian motion with two-valued driftone-dimensional diffusionskew Brownian motionLocal time
Type
Research Article
Information
ESAIM: Probability and Statistics , Volume 18 , 2014 , pp. 686 - 702
Copyright
© EDP Sciences, SMAI 2014

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bally, V. and Talay, D., The law of the Euler scheme for stochastic differential equations: I. Convergence rate of the distribution function. Probab. Theory Related Fields 104 (1996) 43–60. Google Scholar
V.E. Beneš, L.A. Shepp and H.S. Witsenhausen, Some solvable stochastic control problems. In Analysis and optimisation of stochastic systems (Proc. Internat. Conf., Univ. Oxford, Oxford, 1978), Academic Press, London (1980) 3–10.
Beskos, A., Papaspiliopoulos, O. and Roberts, G.O., Retrospective exact simulation of diffusion sample paths with applications. Bernoulli 12 (2006) 1077–1098. Google Scholar
Beskos, A., Papaspiliopoulos, O. and Roberts, G.O., A factorisation of diffusion measure and finite sample path constructions. Methodol. Comput. Appl. Probab. 10 (2008) 85–104. Google Scholar
Beskos, A., Roberts, G., Stuart, A. and Voss, J., MCMC methods for diffusion bridges. Stoch. Dyn. 8 (2008) 319–350. Google Scholar
Beskos, A. and Roberts, G.O., Exact simulation of diffusions. Ann. Appl. Probab. 15 (2005) 2422–2444. Google Scholar
Étoré, P. and Martinez, M., Exact simulation of one-dimensional stochastic differential equations involving the local time at zero of the unknown process. Monte Carlo Methods Appl. 19 (2013) 41–71. Google Scholar
Graversen, S.E. and Shiryaev, A.N., An extension of P. Lévy’s distributional properties to the case of a Brownian motion with drift. Bernoulli 6 (2000) 615–620. Google Scholar
Karatzas, I. and Shreve, S.E., Trivariate density of Brownian motion, its local and occupation times, with application to stochastic control. Ann. Probab. 12 (1984) 819–828. Google Scholar
I. Karatzas and S.E. Shreve, Brownian motion and stochastic calculus, 2nd edn. vol. 113. In Grad. Texts Math. Springer-Verlag, New York (1991) 440–441.
J.-F. Le Gall, One-dimensional stochastic differential equations involving the local times of the unknown process. In Stochastic analysis and applications (Swansea, 1983), Lecture Notes in Math., vol. 1095. Springer, Berlin (1984) 51–82.
V. Reutenauer and E. Tanré, Exact simulation of prices and greeks: application to cir. Preprint (2008).
D. Revuz and M. Yor, Continuous martingales and Brownian motion, 3rd edn. Springer-Verlag (1999).
M. Sbai, Modélisation de la dépendance et simulation de processus en finance. Ph.D. thesis, CERMICS – Centre d’Enseignement et de Recherche en Mathématiques et Calcul Scientifique (2009).