Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Hotz, Thomas
2013.
Geometric Science of Information.
Vol. 8085,
Issue. ,
p.
433.
Weinmann, Andreas
Demaret, Laurent
and
Storath, Martin
2014.
Total Variation Regularization for Manifold-Valued Data.
SIAM Journal on Imaging Sciences,
Vol. 7,
Issue. 4,
p.
2226.
Arnaudon, Marc
and
Miclo, Laurent
2014.
A stochastic algorithm finding generalized means on compact manifolds.
Stochastic Processes and their Applications,
Vol. 124,
Issue. 10,
p.
3463.
Pham, Minh-Tri
Woodford, Oliver J.
Perbet, Frank
Maki, Atsuto
Gherardi, Riccardo
Stenger, Björn
and
Cipolla, Roberto
2015.
Distances and Means of Direct Similarities.
International Journal of Computer Vision,
Vol. 112,
Issue. 3,
p.
285.
Arnaudon, Marc
and
Miclo, Laurent
2016.
A stochastic algorithm finding $p$-means on the circle.
Bernoulli,
Vol. 22,
Issue. 4,
Said, Salem
Hajri, Hatem
Bombrun, Lionel
and
Vemuri, Baba C.
2018.
Gaussian Distributions on Riemannian Symmetric Spaces: Statistical Learning With Structured Covariance Matrices.
IEEE Transactions on Information Theory,
Vol. 64,
Issue. 2,
p.
752.
Gadat, Sébastien
Gavra, Ioana
and
Risser, Laurent
2018.
How to Calculate the Barycenter of a Weighted Graph.
Mathematics of Operations Research,
Vol. 43,
Issue. 4,
p.
1085.
Eichfelder, Gabriele
Hotz, Thomas
and
Wieditz, Johannes
2019.
An algorithm for computing Fréchet means on the sphere.
Optimization Letters,
Vol. 13,
Issue. 7,
p.
1523.
Eltzner, Benjamin
and
Huckemann, Stephan F.
2019.
A smeary central limit theorem for manifolds with application to high-dimensional spheres.
The Annals of Statistics,
Vol. 47,
Issue. 6,
Huckemann, Stephan F.
and
Eltzner, Benjamin
2021.
Data analysis on nonstandard spaces.
WIREs Computational Statistics,
Vol. 13,
Issue. 3,
Mardia, Kanti V.
Wiechers, Henrik
Eltzner, Benjamin
and
Huckemann, Stephan F.
2022.
Principal component analysis and clustering on manifolds.
Journal of Multivariate Analysis,
Vol. 188,
Issue. ,
p.
104862.
Eltzner, Benjamin
2022.
Geometrical smeariness – a new phenomenon of Fréchet means.
Bernoulli,
Vol. 28,
Issue. 1,
Wiechers, Henrik
Eltzner, Benjamin
Mardia, Kanti V
and
Huckemann, Stephan F
2023.
Learning torus PCA-based classification for multiscale RNA correction with application to SARS-CoV-2.
Journal of the Royal Statistical Society Series C: Applied Statistics,
Vol. 72,
Issue. 2,
p.
271.
Gerald, Thomas
Zaatiti, Hadi
Hajri, Hatem
Baskiotis, Nicolas
and
Schwander, Olivier
2023.
A hyperbolic approach for learning communities on graphs.
Data Mining and Knowledge Discovery,
Vol. 37,
Issue. 3,
p.
1090.
Harms, Philipp
Michor, Peter W.
Pennec, Xavier
and
Sommer, Stefan
2023.
Geometry of sample spaces.
Differential Geometry and its Applications,
Vol. 90,
Issue. ,
p.
102029.
Koundouri, P.
Papayiannis, G. I.
Petracou, E. V.
and
Yannacopoulos, A. N.
2024.
Consensus Group Decision Making Under Model Uncertainty with a View Towards Environmental Policy Making.
Environmental and Resource Economics,
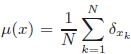 μ(x)=1N∑k=1Nδxk has a unique p–mean ep(x).
As a consequence, if X = (X1,...,XN)
is a MN-valued random
variable with absolutely continuous law, then almost surely μ(X(ω)) has a
unique p–mean. In particular if (Xn)n ≥ 1
is an independent sample of an absolutely continuous law in M, then the process
ep,n(ω) = ep(X1(ω),...,Xn(ω))
is well-defined. Assume M is compact and consider a probability measure
ν in
M. Using
partial simulated annealing, we define a continuous semimartingale which converges in
probability to the set of minimizers of the integral of distance at power p with respect to
ν. When the
set is a singleton, it converges to the p–mean.
μ(x)=1N∑k=1Nδxk has a unique p–mean ep(x).
As a consequence, if X = (X1,...,XN)
is a MN-valued random
variable with absolutely continuous law, then almost surely μ(X(ω)) has a
unique p–mean. In particular if (Xn)n ≥ 1
is an independent sample of an absolutely continuous law in M, then the process
ep,n(ω) = ep(X1(ω),...,Xn(ω))
is well-defined. Assume M is compact and consider a probability measure
ν in
M. Using
partial simulated annealing, we define a continuous semimartingale which converges in
probability to the set of minimizers of the integral of distance at power p with respect to
ν. When the
set is a singleton, it converges to the p–mean.



