We introduce and analyze a numerical strategy to approximate effective coefficients in stochastic homogenization of discrete elliptic equations. In particular, we consider the simplest case possible: An elliptic equation on the d-dimensional lattice $\mathbb{Z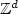}^d$ with independent and identically distributed conductivities on the associated edges. Recent results by Otto and the author quantify the error made by approximating the homogenized coefficient by the averaged energy of a regularized corrector (with parameter T) on some box of finite size L. In this article, we replace the regularized corrector (which is the solution of a problem posed on $\mathbb{Z}^d$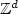) by some practically computable proxy on some box of size R≥L, and quantify the associated additional error. In order to improve the convergence, one may also consider N independent realizations of the computable proxy, and take the empirical average of the associated approximate homogenized coefficients. A natural optimization problem consists in properly choosing T, R, L and N in order to reduce the error at given computational complexity. Our analysis is sharp and sheds some light on this question. In particular, we propose and analyze a numerical algorithm to approximate the homogenized coefficients, taking advantage of the (nearly) optimal scalings of the errors we derive. The efficiency of the approach is illustrated by a numerical study in dimension 2.