Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Schneider, R.
Reichmann, O.
and
Schwab, C.
2010.
Wavelet solution of variable order pseudodifferential equations.
Calcolo,
Vol. 47,
Issue. 2,
p.
65.
PHAM, T. D.
TRAN, T.
and
CHERNOV, A.
2011.
PSEUDODIFFERENTIAL EQUATIONS ON THE SPHERE WITH SPHERICAL SPLINES.
Mathematical Models and Methods in Applied Sciences,
Vol. 21,
Issue. 09,
p.
1933.
Chernov, Alexey
and
Schwab, Christoph
2012.
Exponential Convergence of Gauss--Jacobi Quadratures for Singular Integrals over Simplices in Arbitrary Dimension.
SIAM Journal on Numerical Analysis,
Vol. 50,
Issue. 3,
p.
1433.
HOANG, VIET HA
and
SCHWAB, CHRISTOPH
2012.
REGULARITY AND GENERALIZED POLYNOMIAL CHAOS APPROXIMATION OF PARAMETRIC AND RANDOM SECOND-ORDER HYPERBOLIC PARTIAL DIFFERENTIAL EQUATIONS.
Analysis and Applications,
Vol. 10,
Issue. 03,
p.
295.
MARAZZINA, DANIELE
REICHMANN, OLEG
and
SCHWAB, CHRISTOPH
2012.
hp-DGFEM FOR KOLMOGOROV–FOKKER–PLANCK EQUATIONS OF MULTIVARIATE LÉVY PROCESSES.
Mathematical Models and Methods in Applied Sciences,
Vol. 22,
Issue. 01,
Bremer, James
and
Gimbutas, Zydrunas
2012.
A Nyström method for weakly singular integral operators on surfaces.
Journal of Computational Physics,
Vol. 231,
Issue. 14,
p.
4885.
Karkulik, Michael
Of, Günther
and
Praetorius, Dirk
2013.
Convergence of adaptive 3D BEM for weakly singular integral equations based on isotropic mesh‐refinement.
Numerical Methods for Partial Differential Equations,
Vol. 29,
Issue. 6,
p.
2081.
Bremer, James
and
Gimbutas, Zydrunas
2013.
On the numerical evaluation of the singular integrals of scattering theory.
Journal of Computational Physics,
Vol. 251,
Issue. ,
p.
327.
Chernov, Alexey
and
Reinarz, Anne
2013.
Numerical quadrature for high-dimensional singular integrals over parallelotopes.
Computers & Mathematics with Applications,
Vol. 66,
Issue. 7,
p.
1213.
Sauter, S.
and
Veit, A.
2013.
A Galerkin method for retarded boundary integral equations with smooth and compactly supported temporal basis functions.
Numerische Mathematik,
Vol. 123,
Issue. 1,
p.
145.
Chernov, Alexey
von Petersdorff, Tobias
and
Schwab, Christoph
2015.
Quadrature algorithms for high dimensional singular integrands on simplices.
Numerical Algorithms,
Vol. 70,
Issue. 4,
p.
847.
Dauge, Monique
Düster, Alexander
and
Rank, Ernst
2015.
Theoretical and Numerical Investigation of the Finite Cell Method.
Journal of Scientific Computing,
Vol. 65,
Issue. 3,
p.
1039.
Śmigaj, Wojciech
Betcke, Timo
Arridge, Simon
Phillips, Joel
and
Schweiger, Martin
2015.
Solving Boundary Integral Problems with BEM++.
ACM Transactions on Mathematical Software,
Vol. 41,
Issue. 2,
p.
1.
Feischl, Michael
Führer, Thomas
Heuer, Norbert
Karkulik, Michael
and
Praetorius, Dirk
2015.
Adaptive Boundary Element Methods.
Archives of Computational Methods in Engineering,
Vol. 22,
Issue. 3,
p.
309.
Schwab, Christoph
2015.
Spectral and High Order Methods for Partial Differential Equations ICOSAHOM 2014.
Vol. 106,
Issue. ,
p.
435.
Ainsworth, Mark
and
Glusa, Christian
2017.
Aspects of an adaptive finite element method for the fractional Laplacian: A priori and a posteriori error estimates, efficient implementation and multigrid solver.
Computer Methods in Applied Mechanics and Engineering,
Vol. 327,
Issue. ,
p.
4.
Opschoor, Joost A. A.
Petersen, Philipp C.
and
Schwab, Christoph
2020.
Deep ReLU networks and high-order finite element methods.
Analysis and Applications,
Vol. 18,
Issue. 05,
p.
715.
Opmeer, Mark R.
2020.
Decay of singular values for infinite-dimensional systems with Gevrey regularity.
Systems & Control Letters,
Vol. 137,
Issue. ,
p.
104644.
Feischl, M.
and
Schwab, Ch.
2020.
Exponential convergence in $$H^1$$ of hp-FEM for Gevrey regularity with isotropic singularities.
Numerische Mathematik,
Vol. 144,
Issue. 2,
p.
323.
D’Elia, Marta
Du, Qiang
Glusa, Christian
Gunzburger, Max
Tian, Xiaochuan
and
Zhou, Zhi
2020.
Numerical methods for nonlocal and fractional models.
Acta Numerica,
Vol. 29,
Issue. ,
p.
1.
 require
the evaluation of integrals $I = \int_{S^{(1)}}\int_{S^{(2)}}g(x,y){\rm d}y{\rm d}x$
require
the evaluation of integrals $I = \int_{S^{(1)}}\int_{S^{(2)}}g(x,y){\rm d}y{\rm d}x$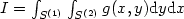 where S(1),S(2) are d-simplices and g has a singularity
at x = y. We assume that g is Gevrey smooth for x$\ne$
where S(1),S(2) are d-simplices and g has a singularity
at x = y. We assume that g is Gevrey smooth for x$\ne$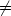 y and
satisfies bounds for the derivatives which allow algebraic singularities
at x = y. This holds for kernel functions commonly occurring in integral
equations. We construct a family of quadrature rules $\mathcal{Q}_{N}$
y and
satisfies bounds for the derivatives which allow algebraic singularities
at x = y. This holds for kernel functions commonly occurring in integral
equations. We construct a family of quadrature rules $\mathcal{Q}_{N}$ using
N function evaluations of g which achieves exponential convergence
|I – $\mathcal{Q}_{N}$
using
N function evaluations of g which achieves exponential convergence
|I – $\mathcal{Q}_{N}$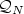 | ≤C exp(–rNγ) with constants r, γ > 0.
| ≤C exp(–rNγ) with constants r, γ > 0.




