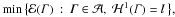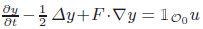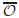Research Article
Shape optimization problems for metric graphs
-
- Published online by Cambridge University Press:
- 29 August 2013, pp. 1-22
-
- Article
- Export citation
Controllability of Schrödinger equation with a nonlocal term
-
- Published online by Cambridge University Press:
- 29 August 2013, pp. 23-41
-
- Article
- Export citation
Dimension reduction for −Δ1
-
- Published online by Cambridge University Press:
- 03 September 2013, pp. 42-77
-
- Article
- Export citation
Differential games of partial information forward-backward doubly SDE and applications∗
-
- Published online by Cambridge University Press:
- 10 October 2013, pp. 78-94
-
- Article
- Export citation
Approximation of the pareto optimal set for multiobjective optimal control problems using viability kernels
-
- Published online by Cambridge University Press:
- 10 October 2013, pp. 95-115
-
- Article
- Export citation
A singular controllability problem with vanishing viscosity
-
- Published online by Cambridge University Press:
- 10 December 2013, pp. 116-140
-
- Article
- Export citation
Pointwise constrained radially increasing minimizers in the quasi-scalar calculus of variations∗
-
- Published online by Cambridge University Press:
- 10 December 2013, pp. 141-157
-
- Article
- Export citation
Some necessary and sufficient conditions for the output controllability of temporal Boolean control networks
-
- Published online by Cambridge University Press:
- 23 December 2013, pp. 158-173
-
- Article
- Export citation
Uniform stabilization of some damped second order evolution equations with vanishing short memory
-
- Published online by Cambridge University Press:
- 23 December 2013, pp. 174-189
-
- Article
- Export citation
Variational approximation of a functional of Mumford–Shah type in codimension higher than one
-
- Published online by Cambridge University Press:
- 27 January 2014, pp. 190-221
-
- Article
- Export citation
Exact null internal controllability for the heat equation on unbounded convex domains∗
-
- Published online by Cambridge University Press:
- 27 January 2014, pp. 222-235
-
- Article
- Export citation
Controllability of 3D low Reynolds number swimmers
-
- Published online by Cambridge University Press:
- 27 January 2014, pp. 236-268
-
- Article
- Export citation
Periodic stabilization for linear time-periodic ordinary differential equations∗∗∗
-
- Published online by Cambridge University Press:
- 27 January 2014, pp. 269-314
-
- Article
- Export citation