Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Aubin, Jean-Pierre
2001.
Viability Kernels and Capture Basins of Sets Under Differential Inclusions.
SIAM Journal on Control and Optimization,
Vol. 40,
Issue. 3,
p.
853.
Penot, Jean-Paul
and
Zălinescu, Constantin
2004.
Continuity of the Legendre–Fenchel transform for some variational convergences.
Optimization,
Vol. 53,
Issue. 5-6,
p.
549.
Camilli, Fabio
and
Siconolfi, Antonio
2005.
Time-Dependent Measurable Hamilton–Jacobi Equations.
Communications in Partial Differential Equations,
Vol. 30,
Issue. 5-6,
p.
813.
Quincampoix, Marc
and
Zlateva, Nadia
2006.
On Lipschitz regularity of minimizers of a calculus of variations problem with non locally bounded Lagrangians.
Comptes Rendus Mathematique,
Vol. 343,
Issue. 1,
p.
69.
COCLITE, GIUSEPPE MARIA
and
RISEBRO, NILS HENRIK
2007.
VISCOSITY SOLUTIONS OF HAMILTON–JACOBI EQUATIONS WITH DISCONTINUOUS COEFFICIENTS.
Journal of Hyperbolic Differential Equations,
Vol. 04,
Issue. 04,
p.
771.
Davini, Andrea
2007.
Bolza Problems with Discontinuous Lagrangians and Lipschitz-Continuity of the Value Function.
SIAM Journal on Control and Optimization,
Vol. 46,
Issue. 5,
p.
1897.
Sieniutycz, Stanislaw
2009.
Dynamic programming and Lagrange multipliers for active relaxation of resources in nonlinear non-equilibrium systems.
Applied Mathematical Modelling,
Vol. 33,
Issue. 3,
p.
1457.
2009.
Energy Optimization in Process Systems.
p.
659.
2013.
Energy Optimization in Process Systems and Fuel Cells.
p.
697.
Rao, Zhiping
and
Zidani, Hasnaa
2013.
Control and Optimization with PDE Constraints.
Vol. 164,
Issue. ,
p.
93.
Imbert, Cyril
Monneau, Régis
and
Zidani, Hasnaa
2013.
A Hamilton-Jacobi approach to junction problems and application to traffic flows.
ESAIM: Control, Optimisation and Calculus of Variations,
Vol. 19,
Issue. 1,
p.
129.
Misztela, A.
2014.
The value function representing Hamilton–Jacobi equation with Hamiltonian depending on value of solution.
ESAIM: Control, Optimisation and Calculus of Variations,
Vol. 20,
Issue. 3,
p.
771.
Festa, Adriano
and
Falcone, Maurizio
2014.
An Approximation Scheme for an Eikonal Equation with Discontinuous Coefficient.
SIAM Journal on Numerical Analysis,
Vol. 52,
Issue. 1,
p.
236.
Cannarsa, P.
and
Frankowska, H.
2014.
From pointwise to local regularity for solutions of Hamilton–Jacobi equations.
Calculus of Variations and Partial Differential Equations,
Vol. 49,
Issue. 3-4,
p.
1061.
Bardi, Martino
Cesaroni, Annalisa
and
Ghilli, Daria
2015.
Large deviations for some fast
stochastic volatility models by viscosity methods.
Discrete & Continuous Dynamical Systems - A,
Vol. 35,
Issue. 9,
p.
3965.
Davini, Andrea
and
Siconolfi, Antonio
2016.
Existence and regularity of strict critical subsolutions in the stationary ergodic setting.
Annales de l'Institut Henri Poincaré C, Analyse non linéaire,
Vol. 33,
Issue. 2,
p.
243.
Misztela, Arkadiusz
2018.
On Nonuniqueness of Solutions of Hamilton–Jacobi–Bellman Equations.
Applied Mathematics & Optimization,
Vol. 77,
Issue. 3,
p.
599.
2018.
Energy Optimization in Process Systems and Fuel Cells.
p.
683.
Misztela, Arkadiusz
2020.
Representation of Hamilton–Jacobi Equation in Optimal Control Theory with Unbounded Control Set.
Journal of Optimization Theory and Applications,
Vol. 185,
Issue. 2,
p.
361.
Bayraktar, Erhan
and
Keller, Christian
2022.
Path-Dependent Hamilton--Jacobi Equations with Super-Quadratic Growth in the Gradient and the Vanishing Viscosity Method.
SIAM Journal on Control and Optimization,
Vol. 60,
Issue. 3,
p.
1690.
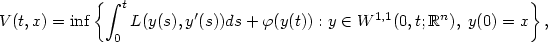 with a lower semicontinuous Lagrangian L and a final cost $ \varphi $
with a lower semicontinuous Lagrangian L and a final cost $ \varphi $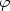 ,
and
show that it is locally Lipschitz for t>0
whenever L is locally bounded. It also satisfies
Hamilton-Jacobi inequalities in a generalized sense.
When the Lagrangian is continuous, then the value function is the
unique lower semicontinuous solution
to the corresponding Hamilton-Jacobi equation, while for discontinuous
Lagrangian we characterize the value function by using the so
called contingent inequalities.
,
and
show that it is locally Lipschitz for t>0
whenever L is locally bounded. It also satisfies
Hamilton-Jacobi inequalities in a generalized sense.
When the Lagrangian is continuous, then the value function is the
unique lower semicontinuous solution
to the corresponding Hamilton-Jacobi equation, while for discontinuous
Lagrangian we characterize the value function by using the so
called contingent inequalities.




