We study the H–1-norm of the function 1 on tubular neighbourhoods of curves in ${\mathbb R}^{2}$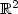. We take the limit of small thickness ε, and we prove two different asymptotic results. The first is an asymptotic development for a fixed curve in the limit ε → 0, containing contributions from the length of the curve (at order ε3), the ends (ε4), and the curvature (ε5). The second result is a Γ-convergence result, in which the central curve may vary along the sequence ε → 0. We prove that a rescaled version of the H–1-norm, which focuses on the ε5 curvature term, Γ-converges to the L2-norm of curvature. In addition, sequences along which the rescaled norm is bounded are compact in the W1,2-topology. Our main tools are the maximum principle for elliptic equations and the use of appropriate trial functions in the variational characterisation of the H–1-norm. For the Γ-convergence result we use the theory of systems of curves without transverse crossings to handle potential intersections in the limit.