In this paper, we consider probability measures μ and ν on a d-dimensional sphere in ${\bf R}^{d+1}, d \geq 1,$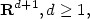 and cost functions of the form $c({\bf x},{\bf y})=l(\frac{|{\bf x}-{\bf y}|^2}{2})$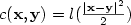 that generalize those arising in geometric optics where $l(t)=-\log t.$ 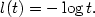We prove that if μ and ν vanish on $(d-1)$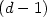-rectifiable sets, if |l'(t)|>0,$\lim_{t\rightarrow 0^+}l(t)=+\infty,$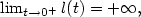 and $g(t):=t(2-t)(l'(t))^2$ 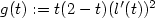is monotone then there exists a unique optimal map To that transports μ onto $\nu,$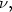 where optimality is measured against c. Furthermore, $\inf_{{\bf x}}|T_o{\bf x}-{\bf x}|>0.$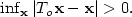 Our approach is based on direct variational arguments. In the special case when $l(t)=-\log t,$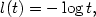 existence of optimal maps on the sphere was obtained earlier in [Glimm and Oliker, J. Math. Sci.117 (2003) 4096-4108] and [Wang, Calculus of Variations and PDE's20 (2004) 329-341] under more restrictive assumptions. In these studies, it was assumed that either μ and ν are absolutely continuous with respect to the d-dimensional Haussdorff measure, or they have disjoint supports. Another aspect of interest in this work is that it is in contrast with the work in [Gangbo and McCann, Quart. Appl. Math.58 (2000) 705-737] where it is proved that when l(t)=t then existence of an optimal map fails when μ and ν are supported by Jordan surfaces.