Hostname: page-component-7479d7b7d-pfhbr Total loading time: 0 Render date: 2024-07-10T04:44:40.499Z Has data issue: false hasContentIssue false
  • English
  • Français

Symbolic dynamics on amenable groups: the entropy of generic shifts

Published online by Cambridge University Press:  28 January 2016

JOSHUA FRISCH  and
OMER TAMUZ
JOSHUA FRISCH
Affiliation:
Department of Mathematics, Massachusetts Institute of Technology, Cambridge, MA 02139, USA email omertamuz@gmail.com
OMER TAMUZ
Affiliation:
Department of Mathematics, Massachusetts Institute of Technology, Cambridge, MA 02139, USA email omertamuz@gmail.com
Get access Rights & Permissions [Opens in a new window]

Abstract

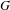Let $G$ be a finitely generated amenable group. We study the space of shifts on 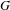$G$ over a given finite alphabet $A$. We show that the zero entropy shifts are generic in this space, and that, more generally, the shifts of entropy $c$ are generic in the space of shifts with entropy at least $c$. The same is shown to hold for the space of transitive shifts and for the space of weakly mixing shifts. As applications of this result, we show that, for every entropy value 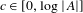$c\in [0,\log |A|]$, there is a weakly mixing subshift of 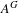$A^{G}$ with entropy $c$. We also show that the set of strongly irreducible shifts does not form a 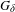$G_{\unicode[STIX]{x1D6FF}}$ in the space of shifts, and that all non-trivial, strongly irreducible shifts are non-isolated points in this space.

Type
Research Article
Information
Ergodic Theory and Dynamical Systems , Volume 37 , Issue 4 , June 2017 , pp. 1187 - 1210
Copyright
© Cambridge University Press, 2016 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Ceccherini-Silberstein, T. and Coornaert, M.. Cellular Automata and Groups. Springer, New York, 2010.Google Scholar
Ceccherini-Silberstein, T. and Coornaert, M.. The myhill property for strongly irreducible subshifts over amenable groups. Monatsh. Math. 165(2) (2012), 155–172.Google Scholar
Coornaert, M.. Topological Dimension and Dynamical Systems. Springer, 2015 (to appear)http://link.springer.com/book/10.1007/978-3-319-19794-4.CrossRefGoogle Scholar
Downarowicz, T., Huczek, D. and Zhang, G.. Tilings of amenable groups. Preprint, 2015, arXiv:1502.02413.Google Scholar
Halmos, P.. In general a measure preserving transformation is mixing. Ann. of Math. (2) 45 (1944), 786–792.Google Scholar
Hochman, M.. Genericity in topological dynamics. Ergod. Th. & Dynam. Sys. 28(1) (2008), 125–165.Google Scholar
Lindenstrauss, E. and Weiss, B.. Mean topological dimension. Israel J. Math. 115(1) (2000), 1–24.Google Scholar
Ornstein, D. and Weiss, B.. Entropy and isomorphism theorems for actions of amenable groups. J. Anal. Math. 48(1) (1987), 1–141.CrossRefGoogle Scholar
Rohlin, V.. A ‘general’ measure-preserving transformation is not mixing. Dokl. Akad. Nauk SSSR (N.S.) 60 (1948), 349–351.Google Scholar
Weiss, B.. Intrinsically ergodic systems. Bull. Amer. Math. Soc. (N.S.) 76(6) (1970), 1266–1269.CrossRefGoogle Scholar