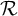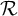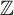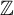1 Introduction
Let
![]() $G=(G,+)$
be a countable discrete abelian group and let
$G=(G,+)$
be a countable discrete abelian group and let
![]() $(T_g)_{g\in G}$
be a measure-preserving G-action on a separable probability space
$(T_g)_{g\in G}$
be a measure-preserving G-action on a separable probability space
![]() $(X,\mathcal A,\mu )$
. We will call the quadruple
$(X,\mathcal A,\mu )$
. We will call the quadruple
![]() $(X,\mathcal A,\mu , (T_g)_{g\in G})$
a measure-preserving system. A measure-preserving system
$(X,\mathcal A,\mu , (T_g)_{g\in G})$
a measure-preserving system. A measure-preserving system
![]() $(X,\mathcal A,\mu , (T_g)_{g\in G})$
is strongly mixing (or 2-mixing) if for any
$(X,\mathcal A,\mu , (T_g)_{g\in G})$
is strongly mixing (or 2-mixing) if for any
![]() $A_0,A_1\in \mathcal A$
, one has
$A_0,A_1\in \mathcal A$
, one has
The goal of this paper is to obtain new results about higher-order mixing properties of strongly mixing actions of abelian groups. These results are motivated by the following classical problem going back to Rohlin (who formulated it for
![]() ${\mathbb {Z}}$
-actions; see [Reference Rohlin27]).
${\mathbb {Z}}$
-actions; see [Reference Rohlin27]).
Rohlin’s Problem. Assume that a measure-preserving system
![]() $(X,\mathcal A,\mu , (T_g)_{g\in G})$
is strongly mixing. Is it true that, given any
$(X,\mathcal A,\mu , (T_g)_{g\in G})$
is strongly mixing. Is it true that, given any
![]() $\ell \geq 2$
, the system
$\ell \geq 2$
, the system
![]() $(X,\mathcal A,\mu , (T_g)_{g\in G})$
is
$(X,\mathcal A,\mu , (T_g)_{g\in G})$
is
![]() $(\ell +1)$
-mixing? This would mean that for any
$(\ell +1)$
-mixing? This would mean that for any
![]() $A_0,\ldots ,A_{\ell }\in \mathcal A$
and any sequences
$A_0,\ldots ,A_{\ell }\in \mathcal A$
and any sequences
![]() $(g^{(1)}_k)_{k\in {\mathbb {N}}},\ldots,$
$(g^{(1)}_k)_{k\in {\mathbb {N}}},\ldots,$
![]() $(g^{(\ell )}_k)_{k\in {\mathbb {N}}}$
in G satisfying that,
$(g^{(\ell )}_k)_{k\in {\mathbb {N}}}$
in G satisfying that,
-
(i) for any
 $j\in \{1,\ldots ,\ell \}$
, (1.2)
$j\in \{1,\ldots ,\ell \}$
, (1.2) $$ \begin{align} \lim_{k\rightarrow\infty}g^{(j)}_k=\infty, \end{align} $$
$$ \begin{align} \lim_{k\rightarrow\infty}g^{(j)}_k=\infty, \end{align} $$
-
(ii) and, for any distinct
 $i,j\in \{1,\ldots ,\ell \}$
, (1.3)
$i,j\in \{1,\ldots ,\ell \}$
, (1.3) $$ \begin{align} \lim_{k\rightarrow\infty}(g^{(j)}_k-g^{(i)}_k)=\infty, \end{align} $$
$$ \begin{align} \lim_{k\rightarrow\infty}(g^{(j)}_k-g^{(i)}_k)=\infty, \end{align} $$
one has
 $$ \begin{align} \lim_{k\rightarrow\infty}\mu(A_0\cap T_{g^{(1)}_k}A_1\cap\cdots\cap T_{g^{(\ell)}_k}A_{\ell})=\prod_{j=0}^{\ell}\mu(A_j). \end{align} $$
$$ \begin{align} \lim_{k\rightarrow\infty}\mu(A_0\cap T_{g^{(1)}_k}A_1\cap\cdots\cap T_{g^{(\ell)}_k}A_{\ell})=\prod_{j=0}^{\ell}\mu(A_j). \end{align} $$
While for
![]() ${\mathbb {Z}}$
-actions Rohlin’s problem is still unsolved, an example for
${\mathbb {Z}}$
-actions Rohlin’s problem is still unsolved, an example for
![]() ${\mathbb {Z}}^2$
-actions, due to Ledrappier, shows that, in general, mixing does not imply mixing of higher orders [Reference Ledrappier22] (the reader is referred to [Reference Schmidt30] for more Ledrappier-type examples for
${\mathbb {Z}}^2$
-actions, due to Ledrappier, shows that, in general, mixing does not imply mixing of higher orders [Reference Ledrappier22] (the reader is referred to [Reference Schmidt30] for more Ledrappier-type examples for
![]() ${\mathbb {Z}}^d$
-actions). More precisely, Ledrappier provided an example of a pair
${\mathbb {Z}}^d$
-actions). More precisely, Ledrappier provided an example of a pair
![]() $S,T$
of commuting mixing automorphisms of a compact abelian group X such that, for some measurable set
$S,T$
of commuting mixing automorphisms of a compact abelian group X such that, for some measurable set
![]() $A\subseteq X$
,
$A\subseteq X$
,
where
![]() $\mu $
is the normalized Haar measure on X. The analysis of Ledrappier’s example undertaken in [Reference Arenas-Carmona, Berend and Bergelson1] reveals that Ledrappier’s system is ‘almost mixing of all orders’ in the sense that, for any
$\mu $
is the normalized Haar measure on X. The analysis of Ledrappier’s example undertaken in [Reference Arenas-Carmona, Berend and Bergelson1] reveals that Ledrappier’s system is ‘almost mixing of all orders’ in the sense that, for any
![]() $\ell \in {\mathbb {N}}$
, if the sequences
$\ell \in {\mathbb {N}}$
, if the sequences
![]() $(g_k^{(1)})_{k\in {\mathbb {N}}},\ldots,$
$(g_k^{(1)})_{k\in {\mathbb {N}}},\ldots,$
![]() $(g_k^{(\ell )})_{k\in {\mathbb {N}}}$
in
$(g_k^{(\ell )})_{k\in {\mathbb {N}}}$
in
![]() ${\mathbb {Z}}^2$
satisfy (1.2) and (1.3) and, in addition, the
${\mathbb {Z}}^2$
satisfy (1.2) and (1.3) and, in addition, the
![]() $\ell $
-tuples
$\ell $
-tuples
![]() $(g_k^{(1)},\ldots ,g_k^{(\ell )})$
avoid certain rather rarefied subsets of
$(g_k^{(1)},\ldots ,g_k^{(\ell )})$
avoid certain rather rarefied subsets of
![]() ${\mathbb {Z}}^{2\ell }$
, equation (1.4) holds for any measurable
${\mathbb {Z}}^{2\ell }$
, equation (1.4) holds for any measurable
![]() $A_0,\ldots ,A_{\ell }\subseteq X$
(see [Reference Arenas-Carmona, Berend and Bergelson1, Theorem 3.3]). The results obtained in [Reference Arenas-Carmona, Berend and Bergelson1] were extended in [Reference Arenas-Carmona, Berend and Bergelson2] to a rather large family of systems of algebraic origin. The notable classes of
$A_0,\ldots ,A_{\ell }\subseteq X$
(see [Reference Arenas-Carmona, Berend and Bergelson1, Theorem 3.3]). The results obtained in [Reference Arenas-Carmona, Berend and Bergelson1] were extended in [Reference Arenas-Carmona, Berend and Bergelson2] to a rather large family of systems of algebraic origin. The notable classes of
![]() ${\mathbb {Z}}$
-actions for which it is known that 2-mixing implies mixing of all orders include ergodic automorphisms of compact groups [Reference Rohlin27], mixing transformations with singular spectrum [Reference Host18], and mixing actions of finite rank [Reference Kalikow19, Reference Ryzhikov28]. It is also known that some natural actions of various locally compact groups possess the property of mixing of all orders (see, for example, [Reference Fayad and Kanigowski12, Reference Marcus24, Reference Mozes26, Reference Ryzhikov29]).
${\mathbb {Z}}$
-actions for which it is known that 2-mixing implies mixing of all orders include ergodic automorphisms of compact groups [Reference Rohlin27], mixing transformations with singular spectrum [Reference Host18], and mixing actions of finite rank [Reference Kalikow19, Reference Ryzhikov28]. It is also known that some natural actions of various locally compact groups possess the property of mixing of all orders (see, for example, [Reference Fayad and Kanigowski12, Reference Marcus24, Reference Mozes26, Reference Ryzhikov29]).
In view of the results obtained in [Reference Arenas-Carmona, Berend and Bergelson1, Reference Arenas-Carmona, Berend and Bergelson2], one might wonder if it could possibly be true that, similarly to the case of Ledrappier’s system, any strongly mixing action
![]() $(X,\mathcal A,\mu , (T_g)_{g\in G})$
of an abelian group G is, in some sense, almost mixing of all orders. The goal of this paper is to establish a result that can be interpreted as a positive answer to this question.
$(X,\mathcal A,\mu , (T_g)_{g\in G})$
of an abelian group G is, in some sense, almost mixing of all orders. The goal of this paper is to establish a result that can be interpreted as a positive answer to this question.
At this point, we would like to mention that in the special case when
![]() $G={\mathbb {Z}}$
, our main theorem (Theorem 1.21 below) has corollaries (Theorem 1.4 and Corollary 1.12) which provide new non-trivial characterizations of the notion of strong mixing in terms of the largeness of sets of the form
$G={\mathbb {Z}}$
, our main theorem (Theorem 1.21 below) has corollaries (Theorem 1.4 and Corollary 1.12) which provide new non-trivial characterizations of the notion of strong mixing in terms of the largeness of sets of the form
 $$ \begin{align} R^{a_1,\ldots,a_{\ell}}_{\epsilon}(A_0,\ldots,A_{\ell})=\bigg\{n\in{\mathbb{Z}}\,\bigg|\,\,\bigg|\mu(A_0\cap T^{a_1n}A_1\cap\cdots\cap T^{a_{\ell} n}A_{\ell})-\prod_{j=0}^{\ell}\mu(A_j)\bigg|<\epsilon\bigg\} \end{align} $$
$$ \begin{align} R^{a_1,\ldots,a_{\ell}}_{\epsilon}(A_0,\ldots,A_{\ell})=\bigg\{n\in{\mathbb{Z}}\,\bigg|\,\,\bigg|\mu(A_0\cap T^{a_1n}A_1\cap\cdots\cap T^{a_{\ell} n}A_{\ell})-\prod_{j=0}^{\ell}\mu(A_j)\bigg|<\epsilon\bigg\} \end{align} $$
and
 $$ \begin{align} &R_{\epsilon}(A_0,\ldots,A_{\ell})\nonumber\\ &\quad=\bigg\{(n_1,\ldots,n_{\ell})\in {\mathbb{Z}}^{\ell}\,\bigg|\,\,\bigg|\mu(A_0\cap T^{n_1}A_1\cap\cdots \cap T^{n_{\ell}}A_{\ell})-\prod_{j=0}^{\ell} \mu( A_j)\bigg|<\epsilon\bigg\}.\quad \end{align} $$
$$ \begin{align} &R_{\epsilon}(A_0,\ldots,A_{\ell})\nonumber\\ &\quad=\bigg\{(n_1,\ldots,n_{\ell})\in {\mathbb{Z}}^{\ell}\,\bigg|\,\,\bigg|\mu(A_0\cap T^{n_1}A_1\cap\cdots \cap T^{n_{\ell}}A_{\ell})-\prod_{j=0}^{\ell} \mu( A_j)\bigg|<\epsilon\bigg\}.\quad \end{align} $$
So, if it turns out that sets of the form (1.5) and (1.6) are not always cofinite, our results still imply that these sets are large in some natural sense, thereby establishing the validity of the claim that strongly mixing
![]() ${\mathbb {Z}}$
-actions are almost mixing of all orders.
${\mathbb {Z}}$
-actions are almost mixing of all orders.
Let
![]() $(X,\mathcal A,\mu ,(T_g)_{g\in G})$
be a measure-preserving system. Let
$(X,\mathcal A,\mu ,(T_g)_{g\in G})$
be a measure-preserving system. Let
![]() $\ell \in {\mathbb {N}}$
and
$\ell \in {\mathbb {N}}$
and
![]() $\epsilon>0$
. For any
$\epsilon>0$
. For any
![]() $A_0,\ldots ,A_{\ell }\in \mathcal A$
consider the set
$A_0,\ldots ,A_{\ell }\in \mathcal A$
consider the set
 $$ \begin{align} &R_{\epsilon}(A_0,\ldots,A_{\ell})\nonumber\\ &\quad=\bigg\{(g_1,\ldots,g_{\ell})\in G^{\ell}\,\bigg|\,\,\bigg|\mu(A_0\cap T_{g_1}A_1\cap\cdots \cap T_{g_{\ell}}A_{\ell})-\prod_{j=0}^{\ell} \mu( A_j)\bigg|<\epsilon\bigg\}. \end{align} $$
$$ \begin{align} &R_{\epsilon}(A_0,\ldots,A_{\ell})\nonumber\\ &\quad=\bigg\{(g_1,\ldots,g_{\ell})\in G^{\ell}\,\bigg|\,\,\bigg|\mu(A_0\cap T_{g_1}A_1\cap\cdots \cap T_{g_{\ell}}A_{\ell})-\prod_{j=0}^{\ell} \mu( A_j)\bigg|<\epsilon\bigg\}. \end{align} $$
Clearly, the higher is the degree of multiple mixing of the system
![]() $(X,\mathcal A,\mu , (T_g)_{g\in G})$
, the more massive should the set
$(X,\mathcal A,\mu , (T_g)_{g\in G})$
, the more massive should the set
![]() $R_{\epsilon }(A_0,\ldots ,A_{\ell })$
be as a subset of
$R_{\epsilon }(A_0,\ldots ,A_{\ell })$
be as a subset of
![]() $G^{\ell }$
. While, for
$G^{\ell }$
. While, for
![]() $\ell =1$
, the strong mixing property of
$\ell =1$
, the strong mixing property of
![]() $(X,\mathcal A,\mu , (T_g)_{g\in G})$
implies that the set
$(X,\mathcal A,\mu , (T_g)_{g\in G})$
implies that the set
![]() $R_{\epsilon }(A_0,A_1)$
is cofinite, this is no longer the case for
$R_{\epsilon }(A_0,A_1)$
is cofinite, this is no longer the case for
![]() $\ell \geq 2$
even if our system
$\ell \geq 2$
even if our system
![]() $(X,\mathcal A,\mu ,(T_g)_{g\in G})$
is mixing of all orders. For example, for any 3-mixing system and any
$(X,\mathcal A,\mu ,(T_g)_{g\in G})$
is mixing of all orders. For example, for any 3-mixing system and any
![]() $A\in \mathcal A$
with
$A\in \mathcal A$
with
![]() $\mu (A)\in (0,1)$
, one has that, if
$\mu (A)\in (0,1)$
, one has that, if
![]() $\epsilon>0$
is small enough, the set
$\epsilon>0$
is small enough, the set
can only have a finite intersection with any of the ‘lines’
![]() $\{(g,g)\,|\,g\in G\}$
,
$\{(g,g)\,|\,g\in G\}$
,
![]() $\{(g,0)\,|\,g\in G\}$
and
$\{(g,0)\,|\,g\in G\}$
and
![]() $\{(0,g)\,|\,g\in G\}$
.
$\{(0,g)\,|\,g\in G\}$
.
In what follows we will show that, for any mixing system
![]() $(X,\mathcal A,\mu , (T_g)_{g\in G})$
, the subsets of
$(X,\mathcal A,\mu , (T_g)_{g\in G})$
, the subsets of
![]() $G^{\ell }$
which are of the form
$G^{\ell }$
which are of the form
![]() $\mathcal R_{\epsilon }(A_0,\ldots ,A_{\ell })$
possess a strong ubiquity property which we will call
$\mathcal R_{\epsilon }(A_0,\ldots ,A_{\ell })$
possess a strong ubiquity property which we will call
![]() $\tilde {\Sigma }_{\ell }^*$
and which is quite a bit stronger than the properties of largeness associated with weakly and mildly mixing systems. In other words, we will show that for any strongly mixing system the complement of any set of the form
$\tilde {\Sigma }_{\ell }^*$
and which is quite a bit stronger than the properties of largeness associated with weakly and mildly mixing systems. In other words, we will show that for any strongly mixing system the complement of any set of the form
![]() $R_{\epsilon } (A_0,\ldots ,A_{\ell })$
is very ‘small’, giving meaning to the claim that
$R_{\epsilon } (A_0,\ldots ,A_{\ell })$
is very ‘small’, giving meaning to the claim that
![]() $(X,\mathcal A,\mu ,(T_g)_{g\in G})$
is ‘almost strongly mixing’ of all orders. This will be achieved with the help of
$(X,\mathcal A,\mu ,(T_g)_{g\in G})$
is ‘almost strongly mixing’ of all orders. This will be achieved with the help of
![]() $\mathcal R$
-limits, a notion of convergence which is based on a classical combinatorial result due to Ramsey and, as we will see, is adequate for dealing with strongly mixing systems. (In particular, we will show that the
$\mathcal R$
-limits, a notion of convergence which is based on a classical combinatorial result due to Ramsey and, as we will see, is adequate for dealing with strongly mixing systems. (In particular, we will show that the
![]() $\tilde {\Sigma }_{\ell }^*$
property of the sets
$\tilde {\Sigma }_{\ell }^*$
property of the sets
![]() $R_{\epsilon }(A_0,\ldots ,A_{\ell })$
implies the strong mixing of
$R_{\epsilon }(A_0,\ldots ,A_{\ell })$
implies the strong mixing of
![]() $(X,\mathcal A,\mu ,(T_g)_{g\in G}$
).)
$(X,\mathcal A,\mu ,(T_g)_{g\in G}$
).)
We would like to remark that while the results that we obtain are not as sharp as those obtained in [Reference Arenas-Carmona, Berend and Bergelson1, Reference Arenas-Carmona, Berend and Bergelson2], they have the advantage of being applicable to any strongly mixing system
![]() $(X,\mathcal A,\mu ,(T_g)_{g\in G})$
, where G is a countable abelian group. Moreover, as will be demonstrated in §6, the versatility of
$(X,\mathcal A,\mu ,(T_g)_{g\in G})$
, where G is a countable abelian group. Moreover, as will be demonstrated in §6, the versatility of
![]() $\mathcal R$
-limits allows one to obtain new and recover some old results pertaining to multiple recurrence properties of weakly and mildly mixing actions of countable abelian groups. We would also like to mention that, as will be seen in §3, the utilization of
$\mathcal R$
-limits allows one to obtain new and recover some old results pertaining to multiple recurrence properties of weakly and mildly mixing actions of countable abelian groups. We would also like to mention that, as will be seen in §3, the utilization of
![]() $\mathcal R$
-limits brings to life many new equivalent characterizations of strong mixing (some of which bear a strong analogy with the familiar characterizations of weak mixing via convergence in density and mild mixing via IP-convergence).
$\mathcal R$
-limits brings to life many new equivalent characterizations of strong mixing (some of which bear a strong analogy with the familiar characterizations of weak mixing via convergence in density and mild mixing via IP-convergence).
Before introducing the above-mentioned notion of largeness for subsets of
![]() $G^{\ell }$
, we define a related and somewhat simpler notion in G.
$G^{\ell }$
, we define a related and somewhat simpler notion in G.
Definition 1.1. Let
![]() $m\in {\mathbb {N}}$
, let
$m\in {\mathbb {N}}$
, let
![]() $(G,+)$
be a countable abelian group, and let
$(G,+)$
be a countable abelian group, and let
![]() $E\subseteq G$
.
$E\subseteq G$
.
-
(1) We say that E is a
 $\Sigma _m$
set if it is of the form where, for each
$\Sigma _m$
set if it is of the form where, for each $$ \begin{align*}\{g_{k_1}^{(1)}+\cdots+g_{k_m}^{(m)}\,|\,k_1<\cdots<k_m\}\end{align*} $$
$$ \begin{align*}\{g_{k_1}^{(1)}+\cdots+g_{k_m}^{(m)}\,|\,k_1<\cdots<k_m\}\end{align*} $$
 $j\in \{1,\ldots ,m\}$
,
$j\in \{1,\ldots ,m\}$
,
 $(g_k^{(j)})_{k\in {\mathbb {N}}}$
is a sequence in G which satisfies
$(g_k^{(j)})_{k\in {\mathbb {N}}}$
is a sequence in G which satisfies
 $\lim _{k\rightarrow \infty }g_k^{(j)}=\infty $
.
$\lim _{k\rightarrow \infty }g_k^{(j)}=\infty $
.
-
(2) We say that E is a
 $\Sigma _m^*$
set if it has a non-trivial intersection with every
$\Sigma _m^*$
set if it has a non-trivial intersection with every
 $\Sigma _m$
set.
$\Sigma _m$
set.
Remark 1.2
-
(a) Note that a subset of G is
 $\Sigma _1^*$
if and only if it is cofinite. On the other hand, for any
$\Sigma _1^*$
if and only if it is cofinite. On the other hand, for any
 $m\geq 2$
, a
$m\geq 2$
, a
 $\Sigma _m^*$
set does not need to be cofinite. Moreover, one can show that for each
$\Sigma _m^*$
set does not need to be cofinite. Moreover, one can show that for each
 $m\geq 2$
, there exists a
$m\geq 2$
, there exists a
 $\Sigma _{m}^*$
set which fails to be a
$\Sigma _{m}^*$
set which fails to be a
 $\Sigma _{n}^*$
set for each
$\Sigma _{n}^*$
set for each
 $n<m$
[Reference Bergelson and Zelada8].
$n<m$
[Reference Bergelson and Zelada8]. -
(b) The notion of
 $\Sigma _m^*$
is similar to (but much stronger than) the notion of IP
$\Sigma _m^*$
is similar to (but much stronger than) the notion of IP
 $^*$
which has an intrinsic connection to mild mixing and which plays an instrumental role in IP ergodic theory and in Ramsey theory (see, for example, [Reference Bergelson and McCutcheon5, Reference Furstenberg14, Reference Furstenberg and Katznelson15]). The connection between these two notions will be discussed in detail in §5.
$^*$
which has an intrinsic connection to mild mixing and which plays an instrumental role in IP ergodic theory and in Ramsey theory (see, for example, [Reference Bergelson and McCutcheon5, Reference Furstenberg14, Reference Furstenberg and Katznelson15]). The connection between these two notions will be discussed in detail in §5.
Since the sets
![]() $R_{\epsilon }(A_0,\ldots ,A_{\ell })$
are, by definition, subsets of
$R_{\epsilon }(A_0,\ldots ,A_{\ell })$
are, by definition, subsets of
![]() $G^{\ell }$
, the above-defined notion of
$G^{\ell }$
, the above-defined notion of
![]() $\Sigma _m^*$
has to be ‘upgraded’ to the subsets of the Cartesian power
$\Sigma _m^*$
has to be ‘upgraded’ to the subsets of the Cartesian power
![]() $G^{\ell }$
in order to be useful in the study of the asymptotic behavior of multiparameter expressions of the form
$G^{\ell }$
in order to be useful in the study of the asymptotic behavior of multiparameter expressions of the form
However, it is worth noting that the family of
![]() $\Sigma _m^*$
sets is quite adequate for dealing with ‘diagonal’ multicorrelation sequences. In the case
$\Sigma _m^*$
sets is quite adequate for dealing with ‘diagonal’ multicorrelation sequences. In the case
![]() $G={\mathbb {Z}}$
, such diagonal sequences have the form
$G={\mathbb {Z}}$
, such diagonal sequences have the form
where
![]() $a_1,\ldots ,a_{\ell }\in {\mathbb {Z}}$
, and play an instrumental role in Furstenberg’s ergodic approach to Szemerédi’s theorem [Reference Furstenberg13, Reference Furstenberg14]. For example, our main result (Theorem 1.21), while dealing with the multiparameter expressions (1.8), has strong corollaries of a ‘diagonal’ nature. The following theorem (which is a version of Theorem 4.4 below) is an example of a new result of this kind. Note the appearance of
$a_1,\ldots ,a_{\ell }\in {\mathbb {Z}}$
, and play an instrumental role in Furstenberg’s ergodic approach to Szemerédi’s theorem [Reference Furstenberg13, Reference Furstenberg14]. For example, our main result (Theorem 1.21), while dealing with the multiparameter expressions (1.8), has strong corollaries of a ‘diagonal’ nature. The following theorem (which is a version of Theorem 4.4 below) is an example of a new result of this kind. Note the appearance of
![]() $\Sigma _{\ell }^*$
sets in the formulation.
$\Sigma _{\ell }^*$
sets in the formulation.
Theorem 1.3. Let
![]() $(G,+)$
be a countable abelian group, let
$(G,+)$
be a countable abelian group, let
![]() $(X,\mathcal A,\mu ,(T_g)_{g\in G})$
be a strongly mixing system, and let the homomorphisms
$(X,\mathcal A,\mu ,(T_g)_{g\in G})$
be a strongly mixing system, and let the homomorphisms
![]() $\phi _1,\ldots ,\phi _{\ell }:G\rightarrow G$
be such that, for any
$\phi _1,\ldots ,\phi _{\ell }:G\rightarrow G$
be such that, for any
![]() $j\in \{1,\ldots ,\ell \}$
,
$j\in \{1,\ldots ,\ell \}$
,
![]() $\ker (\phi _j)$
is finite and, for any
$\ker (\phi _j)$
is finite and, for any
![]() $i\neq j$
,
$i\neq j$
,
![]() $\ker (\phi _j-\phi _i)$
is also finite. Then, for any
$\ker (\phi _j-\phi _i)$
is also finite. Then, for any
![]() $A_0,\ldots ,A_{\ell }\in \mathcal A$
and any
$A_0,\ldots ,A_{\ell }\in \mathcal A$
and any
![]() $\epsilon>0$
, the set
$\epsilon>0$
, the set
 $$ \begin{align} R_{\epsilon}^{\phi_1,\ldots,\phi_{\ell}}(A_0,\ldots,A_{\ell}) =\bigg\{g\in G\,\bigg|\,\,\bigg|\mu(A_0\cap T_{\phi_1(g)}A_1\cap \cdots \cap T_{\phi_{\ell}(g)}A_{\ell})-\prod_{j=0}^{\ell}\!\mu(A_j)\bigg|<\epsilon\bigg\} \end{align} $$
$$ \begin{align} R_{\epsilon}^{\phi_1,\ldots,\phi_{\ell}}(A_0,\ldots,A_{\ell}) =\bigg\{g\in G\,\bigg|\,\,\bigg|\mu(A_0\cap T_{\phi_1(g)}A_1\cap \cdots \cap T_{\phi_{\ell}(g)}A_{\ell})-\prod_{j=0}^{\ell}\!\mu(A_j)\bigg|<\epsilon\bigg\} \end{align} $$
is
![]() $\Sigma _{\ell }^*$
.
$\Sigma _{\ell }^*$
.
When G is finitely generated, Theorem 1.3 has a stronger version (Theorem 4.2), which in the case
![]() $G={\mathbb {Z}}$
can be formulated as follows.
$G={\mathbb {Z}}$
can be formulated as follows.
Theorem 1.4. Let
![]() $(X,\mathcal A,\mu , T)$
be a measure-preserving system, let
$(X,\mathcal A,\mu , T)$
be a measure-preserving system, let
![]() $\ell \in {\mathbb {N}}$
, and let
$\ell \in {\mathbb {N}}$
, and let
![]() $a_1,\ldots ,a_{\ell }$
be distinct non-zero integers. Then T is strongly mixing if and only if, for any
$a_1,\ldots ,a_{\ell }$
be distinct non-zero integers. Then T is strongly mixing if and only if, for any
![]() $A_0,\ldots ,A_{\ell }\in \mathcal A$
and any
$A_0,\ldots ,A_{\ell }\in \mathcal A$
and any
![]() $\epsilon>0$
, the set
$\epsilon>0$
, the set
 $$ \begin{align} R^{a_1,\ldots,a_{\ell}}_{\epsilon}(A_0,\ldots,A_{\ell})=\bigg\{{\kern-1pt}n\in{\mathbb{Z}}\,\bigg|\,\,\bigg|\mu(A_0\cap T^{a_1n}A_1\cap\cdots\cap T^{a_{\ell} n}A_{\ell})-{\kern-1pt}\prod_{j=0}^{\ell}\mu(A_j)\bigg|{\kern-2pt}<{\kern-1pt}\epsilon{\kern-1pt}\bigg\} \end{align} $$
$$ \begin{align} R^{a_1,\ldots,a_{\ell}}_{\epsilon}(A_0,\ldots,A_{\ell})=\bigg\{{\kern-1pt}n\in{\mathbb{Z}}\,\bigg|\,\,\bigg|\mu(A_0\cap T^{a_1n}A_1\cap\cdots\cap T^{a_{\ell} n}A_{\ell})-{\kern-1pt}\prod_{j=0}^{\ell}\mu(A_j)\bigg|{\kern-2pt}<{\kern-1pt}\epsilon{\kern-1pt}\bigg\} \end{align} $$
is
![]() $\Sigma _{\ell }^*$
.
$\Sigma _{\ell }^*$
.
For a related result see [Reference Bergelson and Zelada7, Theorem 1.11]. See also [Reference Kuang and Ye20].
Remark 1.5. One can view Theorem 1.4 as a strongly mixing analogue of two theorems due to Furstenberg which pertain to weak and mild mixing (see Theorems 4.11 and 9.27 in [Reference Furstenberg14], respectively). The first of these two theorems states that the assumption that
![]() $(X,\mathcal A,\mu , T)$
is weakly mixing implies (and is implied by the fact) that the sets
$(X,\mathcal A,\mu , T)$
is weakly mixing implies (and is implied by the fact) that the sets
![]() $R^{a_1,\ldots ,a_{\ell }}_{\epsilon }(A_0,\ldots ,A_{\ell })$
defined in (1.11) have uniform density one. The second one states that the assumption that
$R^{a_1,\ldots ,a_{\ell }}_{\epsilon }(A_0,\ldots ,A_{\ell })$
defined in (1.11) have uniform density one. The second one states that the assumption that
![]() $(X,\mathcal A,\mu ,T)$
is mildly mixing implies (and is implied by) the IP
$(X,\mathcal A,\mu ,T)$
is mildly mixing implies (and is implied by) the IP
![]() $^*$
property of the sets
$^*$
property of the sets
![]() $R^{a_1,\ldots ,a_{\ell }}_{\epsilon }(A_0,\ldots ,A_{\ell })$
. These theorems are instrumental for the proofs of the ergodic Szemerédi [Reference Furstenberg13] and IP-Szemerédi [Reference Furstenberg and Katznelson15] theorems.
$R^{a_1,\ldots ,a_{\ell }}_{\epsilon }(A_0,\ldots ,A_{\ell })$
. These theorems are instrumental for the proofs of the ergodic Szemerédi [Reference Furstenberg13] and IP-Szemerédi [Reference Furstenberg and Katznelson15] theorems.
Note that, for
![]() $\ell =1$
, both diagonal (see (1.9)) and multiparameter (see (1.8)) multicorrelation sequences reduce to the classical expression
$\ell =1$
, both diagonal (see (1.9)) and multiparameter (see (1.8)) multicorrelation sequences reduce to the classical expression
![]() $\mu (A_0\cap T_{g}A_1)$
. The following theorem (which is a very special case of stronger results to be established in this paper) shows that, even in the rather degenerated case
$\mu (A_0\cap T_{g}A_1)$
. The following theorem (which is a very special case of stronger results to be established in this paper) shows that, even in the rather degenerated case
![]() $\ell =1$
,
$\ell =1$
,
![]() $\Sigma _m^*$
sets provide a new characterization for the notion of strong mixing for actions of abelian groups.
$\Sigma _m^*$
sets provide a new characterization for the notion of strong mixing for actions of abelian groups.
Theorem 1.6. Let
![]() $(G,+)$
be a countable abelian group and let
$(G,+)$
be a countable abelian group and let
![]() $(X,\mathcal A,\mu , (T_g)_{g\in G})$
be a measure-preserving system. The following statements are equivalent.
$(X,\mathcal A,\mu , (T_g)_{g\in G})$
be a measure-preserving system. The following statements are equivalent.
-
(i)
 $(T_g)_{g\in G}$
is strongly mixing. In other words, for any
$(T_g)_{g\in G}$
is strongly mixing. In other words, for any
 $\epsilon>0$
and any
$\epsilon>0$
and any
 $A_0,A_1\in \mathcal A$
, the set is cofinite (that is, it is
$A_0,A_1\in \mathcal A$
, the set is cofinite (that is, it is $$ \begin{align*}R_{\epsilon}(A_0,A_1)=\{g\in G\,|\,|\mu(A_0\cap T_g A_1)-\mu(A_0)\mu(A_1)|<\epsilon\}\end{align*} $$
$$ \begin{align*}R_{\epsilon}(A_0,A_1)=\{g\in G\,|\,|\mu(A_0\cap T_g A_1)-\mu(A_0)\mu(A_1)|<\epsilon\}\end{align*} $$
 $\Sigma _1^*$
in G).
$\Sigma _1^*$
in G).
-
(ii) For any
 $m\in {\mathbb {N}}$
, any
$m\in {\mathbb {N}}$
, any
 $\epsilon>0$
and any
$\epsilon>0$
and any
 $A_0,A_1\in \mathcal A$
, the set
$A_0,A_1\in \mathcal A$
, the set
 $R_{\epsilon }(A_0,A_1)$
is
$R_{\epsilon }(A_0,A_1)$
is
 $\Sigma _m^*$
in G.
$\Sigma _m^*$
in G. -
(iii) There exists an
 $m\in {\mathbb {N}}$
such that, for any
$m\in {\mathbb {N}}$
such that, for any
 $\epsilon>0$
and any
$\epsilon>0$
and any
 $A_0,A_1\in \mathcal A$
, the set
$A_0,A_1\in \mathcal A$
, the set
 $R_{\epsilon }(A_0,A_1)$
is
$R_{\epsilon }(A_0,A_1)$
is
 $\Sigma _m^*$
in G.
$\Sigma _m^*$
in G.
We next define the modified versions of
![]() $\Sigma _m$
and
$\Sigma _m$
and
![]() $\Sigma _m^*$
sets which will be instrumental in dealing with the multiple mixing properties of strongly mixing systems.
$\Sigma _m^*$
sets which will be instrumental in dealing with the multiple mixing properties of strongly mixing systems.
Definition 1.7. Let
![]() $(G,+)$
be a countable abelian group and let
$(G,+)$
be a countable abelian group and let
![]() $(g_k)_{k\in {\mathbb {N}}}$
and
$(g_k)_{k\in {\mathbb {N}}}$
and
![]() $(h_k)_{k\in {\mathbb {N}}}$
be two sequences in G. We say that
$(h_k)_{k\in {\mathbb {N}}}$
be two sequences in G. We say that
![]() $(g_k)_{k\in {\mathbb {N}}}$
and
$(g_k)_{k\in {\mathbb {N}}}$
and
![]() $(h_k)_{k\in {\mathbb {N}}}$
grow apart if
$(h_k)_{k\in {\mathbb {N}}}$
grow apart if
![]() $\lim _{k\rightarrow \infty } (g_k-h_k)=\infty $
.
$\lim _{k\rightarrow \infty } (g_k-h_k)=\infty $
.
Definition 1.8. Let
![]() $(G,+)$
be a countable abelian group, let
$(G,+)$
be a countable abelian group, let
![]() $d\in {\mathbb {N}}$
and let
$d\in {\mathbb {N}}$
and let
![]() $(\textbf g_k)_{k\in {\mathbb {N}}}=(g_{k,1},\ldots ,g_{k,d})_{k\in {\mathbb {N}}}$
be a sequence in
$(\textbf g_k)_{k\in {\mathbb {N}}}=(g_{k,1},\ldots ,g_{k,d})_{k\in {\mathbb {N}}}$
be a sequence in
![]() $G^d$
. We say that
$G^d$
. We say that
![]() $(\textbf g_k)_{k\in {\mathbb {N}}}$
is non-degenerated if, for each
$(\textbf g_k)_{k\in {\mathbb {N}}}$
is non-degenerated if, for each
![]() $j\in \{1,\ldots ,d\}$
,
$j\in \{1,\ldots ,d\}$
,
Definition 1.9. Let
![]() $d,m\in {\mathbb {N}}$
and let
$d,m\in {\mathbb {N}}$
and let
![]() $(G,+)$
be a countable abelian group.
$(G,+)$
be a countable abelian group.
-
(1) We say that
 $E\subseteq G^d$
is a
$E\subseteq G^d$
is a
 $\tilde {\Sigma }_m$
set if it is of the form where, for each
$\tilde {\Sigma }_m$
set if it is of the form where, for each $$ \begin{align*}\{\textbf g_{k_1}^{(1)}+\cdots+\textbf g_{k_m}^{(m)}\,|\,k_1<\cdots<k_m\}\end{align*} $$
$$ \begin{align*}\{\textbf g_{k_1}^{(1)}+\cdots+\textbf g_{k_m}^{(m)}\,|\,k_1<\cdots<k_m\}\end{align*} $$
 $j\in \{1,\ldots ,m\}$
,
$j\in \{1,\ldots ,m\}$
,
 $(\textbf g_k^{(j)})_{k\in {\mathbb {N}}}=(g_{k,1}^{(j)},\ldots ,g_{k,d}^{(j)})_{k\in {\mathbb {N}}}$
is a non- degenerated sequence in
$(\textbf g_k^{(j)})_{k\in {\mathbb {N}}}=(g_{k,1}^{(j)},\ldots ,g_{k,d}^{(j)})_{k\in {\mathbb {N}}}$
is a non- degenerated sequence in
 $G^d$
and for any distinct
$G^d$
and for any distinct
 $t,t'\in \{1,\ldots ,d\}$
the sequences
$t,t'\in \{1,\ldots ,d\}$
the sequences
 $(g_{k,t}^{(j)})_{k\in {\mathbb {N}}}$
and
$(g_{k,t}^{(j)})_{k\in {\mathbb {N}}}$
and
 $(g_{k,t'}^{(j)})_{k\in {\mathbb {N}}}$
grow apart. (Note that if
$(g_{k,t'}^{(j)})_{k\in {\mathbb {N}}}$
grow apart. (Note that if
 $d=1$
, then
$d=1$
, then
 $E\subseteq G$
is a
$E\subseteq G$
is a
 $\Sigma _m$
set if and only if it is a
$\Sigma _m$
set if and only if it is a
 $\tilde {\Sigma }_m$
set.)
$\tilde {\Sigma }_m$
set.)
-
(2) We say that
 $E\subseteq G^d$
is a
$E\subseteq G^d$
is a
 $\tilde \Sigma _m^*$
set if it has a non-trivial intersection with every
$\tilde \Sigma _m^*$
set if it has a non-trivial intersection with every
 $\tilde \Sigma _m$
set in
$\tilde \Sigma _m$
set in
 $G^d$
.
$G^d$
.
Remark 1.10. The main difference between
![]() $\tilde {\Sigma }_m$
sets and
$\tilde {\Sigma }_m$
sets and
![]() $\Sigma _m$
sets is that
$\Sigma _m$
sets is that
![]() $\tilde {\Sigma }_m$
sets are subsets of Cartesian powers of G and have a built-in feature which guarantees that, asymptotically, the elements of
$\tilde {\Sigma }_m$
sets are subsets of Cartesian powers of G and have a built-in feature which guarantees that, asymptotically, the elements of
![]() $\tilde {\Sigma }_m$
sets stay away from ‘degenerated’ subsets such as the following subsets of
$\tilde {\Sigma }_m$
sets stay away from ‘degenerated’ subsets such as the following subsets of
![]() $G^3$
:
$G^3$
:
![]() $\{(g,g,g)\,|\,g\in G\}$
,
$\{(g,g,g)\,|\,g\in G\}$
,
![]() $\{(g,2g,0)\,|\,g\in G\}$
and
$\{(g,2g,0)\,|\,g\in G\}$
and
![]() $\{(g,g,h)\,|\,g, h\in G\}$
.
$\{(g,g,h)\,|\,g, h\in G\}$
.
The following theorem, which is a corollary of Theorem 1.21 below, demonstrates the relevance of
![]() $\tilde {\Sigma }_m$
sets for dealing with mixing of higher orders.
$\tilde {\Sigma }_m$
sets for dealing with mixing of higher orders.
Theorem 1.11. Let
![]() $(G,+)$
be a countable abelian group and let
$(G,+)$
be a countable abelian group and let
![]() $(X,\mathcal A,\mu , (T_g)_{g\in G})$
be a measure-preserving system. The following statements are equivalent.
$(X,\mathcal A,\mu , (T_g)_{g\in G})$
be a measure-preserving system. The following statements are equivalent.
-
(i)
 $(T_g)_{g\in G}$
is strongly mixing.
$(T_g)_{g\in G}$
is strongly mixing. -
(ii) For any
 $\ell \in {\mathbb {N}}$
, any
$\ell \in {\mathbb {N}}$
, any
 $A_0,\ldots ,A_{\ell }\in \mathcal A$
and any
$A_0,\ldots ,A_{\ell }\in \mathcal A$
and any
 $\epsilon>0$
, the set is
$\epsilon>0$
, the set is $$ \begin{align*}&R_{\epsilon}(A_0,\ldots,A_{\ell})\\ &\quad=\bigg\{(g_1,\ldots,g_{\ell})\in G^{\ell}\,\bigg|\,\,\bigg|\mu(A_0\cap T_{g_1}A_1\cap\cdots \cap T_{g_{\ell}}A_{\ell})-\prod_{j=0}^{\ell} \mu( A_j)\bigg|<\epsilon\bigg\} \end{align*} $$
$$ \begin{align*}&R_{\epsilon}(A_0,\ldots,A_{\ell})\\ &\quad=\bigg\{(g_1,\ldots,g_{\ell})\in G^{\ell}\,\bigg|\,\,\bigg|\mu(A_0\cap T_{g_1}A_1\cap\cdots \cap T_{g_{\ell}}A_{\ell})-\prod_{j=0}^{\ell} \mu( A_j)\bigg|<\epsilon\bigg\} \end{align*} $$
 $\tilde {\Sigma }_{\ell }^*$
in
$\tilde {\Sigma }_{\ell }^*$
in
 $G^{\ell }$
.
$G^{\ell }$
.
-
(iii) There exists an
 $\ell \in {\mathbb {N}}$
such that, for any
$\ell \in {\mathbb {N}}$
such that, for any
 $A_0,\ldots ,A_{\ell }\in \mathcal A$
and any
$A_0,\ldots ,A_{\ell }\in \mathcal A$
and any
 $\epsilon>0$
, the set
$\epsilon>0$
, the set
 $R_{\epsilon }(A_0,\ldots ,A_{\ell })$
is
$R_{\epsilon }(A_0,\ldots ,A_{\ell })$
is
 $\tilde {\Sigma }_{\ell }^*$
in
$\tilde {\Sigma }_{\ell }^*$
in
 $G^{\ell }$
.
$G^{\ell }$
.
We take the liberty of stating explicitly the following special case of Theorem 1.11 to stress the applicability of the apparatus developed in this paper to
![]() ${\mathbb {Z}}$
-actions.
${\mathbb {Z}}$
-actions.
Corollary 1.12. Let
![]() $(X,\mathcal A,\mu , T)$
be a measure-preserving system. The following statements are equivalent.
$(X,\mathcal A,\mu , T)$
be a measure-preserving system. The following statements are equivalent.
-
(i) T is strongly mixing.
-
(ii) For any
 $\ell \in {\mathbb {N}}$
, any
$\ell \in {\mathbb {N}}$
, any
 $A_0,\ldots ,A_{\ell }\in \mathcal A$
and any
$A_0,\ldots ,A_{\ell }\in \mathcal A$
and any
 $\epsilon>0$
, the set is
$\epsilon>0$
, the set is $$ \begin{align*}&R_{\epsilon}(A_0,\ldots,A_{\ell})\\ &\quad=\bigg\{(n_1,\ldots,n_{\ell})\in {\mathbb{Z}}^{\ell}\,\bigg|\,\,\bigg|\mu(A_0\cap T^{n_1}A_1\cap\cdots \cap T^{n_{\ell}}A_{\ell})-\prod_{j=0}^{\ell} \mu( A_j)\bigg|<\epsilon\bigg\}\end{align*} $$
$$ \begin{align*}&R_{\epsilon}(A_0,\ldots,A_{\ell})\\ &\quad=\bigg\{(n_1,\ldots,n_{\ell})\in {\mathbb{Z}}^{\ell}\,\bigg|\,\,\bigg|\mu(A_0\cap T^{n_1}A_1\cap\cdots \cap T^{n_{\ell}}A_{\ell})-\prod_{j=0}^{\ell} \mu( A_j)\bigg|<\epsilon\bigg\}\end{align*} $$
 $\tilde {\Sigma }_{\ell }^*$
in
$\tilde {\Sigma }_{\ell }^*$
in
 ${\mathbb {Z}}^{\ell }$
.
${\mathbb {Z}}^{\ell }$
.
-
(iii) There exists an
 $\ell \in {\mathbb {N}}$
such that, for any
$\ell \in {\mathbb {N}}$
such that, for any
 $A_0,\ldots ,A_{\ell }\in \mathcal A$
and any
$A_0,\ldots ,A_{\ell }\in \mathcal A$
and any
 $\epsilon>0$
, the set
$\epsilon>0$
, the set
 $R_{\epsilon }(A_0,\ldots ,A_{\ell })$
is
$R_{\epsilon }(A_0,\ldots ,A_{\ell })$
is
 $\tilde {\Sigma }_{\ell }^*$
in
$\tilde {\Sigma }_{\ell }^*$
in
 ${\mathbb {Z}}^{\ell }$
.
${\mathbb {Z}}^{\ell }$
.
We introduce now the notion of convergence that is utilized in the proof of Theorem 1.11 and is based on the classical Ramsey theorem (which, for convenience of the reader, we state below). We remark that variants of this notion of convergence can also be found in [Reference Bojańczyk, Kopczyński and Toruńczyk10, Reference Campbell and McCutcheon11, Reference Kubiś and Szeptycki21, Reference Lorentz23, Reference McCutcheon25, Reference Sucheston31]. Given
![]() $m\in {\mathbb {N}}$
and an infinite set
$m\in {\mathbb {N}}$
and an infinite set
![]() $S\subseteq {\mathbb {N}}$
, we denote by
$S\subseteq {\mathbb {N}}$
, we denote by
![]() $S^{(m)}$
the family of all m-element subsets of S. When writing
$S^{(m)}$
the family of all m-element subsets of S. When writing
![]() $\{k_1,\ldots ,k_m\}\in S^{(m)}$
, we will always assume that
$\{k_1,\ldots ,k_m\}\in S^{(m)}$
, we will always assume that
![]() $k_1<\cdots <k_m$
.
$k_1<\cdots <k_m$
.
Theorem 1.13. (Ramsey’s theorem)
Let
![]() $r,m\in {\mathbb {N}}$
and let
$r,m\in {\mathbb {N}}$
and let
![]() $C_1,\ldots ,C_r\subseteq {\mathbb {N}}^{(m)}$
be such that
$C_1,\ldots ,C_r\subseteq {\mathbb {N}}^{(m)}$
be such that
 $$ \begin{align} {\mathbb{N}}^{(m)}=\bigcup _{j=1}^r C_j. \end{align} $$
$$ \begin{align} {\mathbb{N}}^{(m)}=\bigcup _{j=1}^r C_j. \end{align} $$
Then there exist
![]() $j_0\in \{1,\ldots ,r\}$
and an infinite subset
$j_0\in \{1,\ldots ,r\}$
and an infinite subset
![]() $S\subseteq {\mathbb {N}}$
satisfying
$S\subseteq {\mathbb {N}}$
satisfying
![]() $S^{(m)}\subseteq C_{j_0}$
.
$S^{(m)}\subseteq C_{j_0}$
.
Remark 1.14. It is easy to see that Theorem 1.13 can be formulated in the following equivalent form that will be frequently used in the sequel.
Let
![]() $r,m\in {\mathbb {N}}$
, let P be an infinite subset of
$r,m\in {\mathbb {N}}$
, let P be an infinite subset of
![]() ${\mathbb {N}}$
and let
${\mathbb {N}}$
and let
![]() $C_1,\ldots ,C_r\subseteq {\mathbb {N}}^{(m)}$
be such that
$C_1,\ldots ,C_r\subseteq {\mathbb {N}}^{(m)}$
be such that
 $$ \begin{align} P^{(m)}\subseteq\bigcup _{j=1}^r C_j. \end{align} $$
$$ \begin{align} P^{(m)}\subseteq\bigcup _{j=1}^r C_j. \end{align} $$
Then there exist
![]() $j_0\in \{1,\ldots ,r\}$
and an infinite subset
$j_0\in \{1,\ldots ,r\}$
and an infinite subset
![]() $S\subseteq P$
satisfying
$S\subseteq P$
satisfying
![]() $S^{(m)}\subseteq ~C_{j_0}$
.
$S^{(m)}\subseteq ~C_{j_0}$
.
Definition 1.15. Let
![]() $m\in {\mathbb {N}}$
, let
$m\in {\mathbb {N}}$
, let
![]() $(X,d)$
be a compact metric space, let
$(X,d)$
be a compact metric space, let
![]() $x\in X$
, let
$x\in X$
, let
![]() $(x_{\alpha })_{\alpha \in {\mathbb {N}}^{(m)}}$
be an
$(x_{\alpha })_{\alpha \in {\mathbb {N}}^{(m)}}$
be an
![]() ${{\mathbb {N}}^{(m)}\text {-sequence}}$
in X, and let S be an infinite subset of
${{\mathbb {N}}^{(m)}\text {-sequence}}$
in X, and let S be an infinite subset of
![]() ${\mathbb {N}}$
. We write
${\mathbb {N}}$
. We write
if, for every
![]() $\epsilon>0$
, there exists
$\epsilon>0$
, there exists
![]() $\alpha _0\in {\mathbb {N}}^{(m)}$
such that, for any
$\alpha _0\in {\mathbb {N}}^{(m)}$
such that, for any
![]() $\alpha \in S^{(m)}$
satisfying
$\alpha \in S^{(m)}$
satisfying
![]() ${\min \alpha>\max \alpha _0}$
, one has
${\min \alpha>\max \alpha _0}$
, one has
The following theorem can be viewed as a version of Bolzano–Weierstrass theorem for
![]() ${\mathcal R\text {-convergence}}$
. It follows from Theorem 1.13 with the help of a diagonalization argument.
${\mathcal R\text {-convergence}}$
. It follows from Theorem 1.13 with the help of a diagonalization argument.
Theorem 1.16. Let
![]() $m\in {\mathbb {N}}$
, let
$m\in {\mathbb {N}}$
, let
![]() $(X,d)$
be a compact metric space and let
$(X,d)$
be a compact metric space and let
![]() $(x_{\alpha })_{\alpha \in {\mathbb {N}}^{(m)}}$
be an
$(x_{\alpha })_{\alpha \in {\mathbb {N}}^{(m)}}$
be an
![]() ${\mathbb {N}}^{(m)}$
-sequence in X. Then, for any infinite set
${\mathbb {N}}^{(m)}$
-sequence in X. Then, for any infinite set
![]() $S_1\subseteq {\mathbb {N}}$
, there exist an
$S_1\subseteq {\mathbb {N}}$
, there exist an
![]() $x\in X$
and an infinite set
$x\in X$
and an infinite set
![]() $S\subseteq S_1$
such that
$S\subseteq S_1$
such that
Remark 1.17. Let
![]() $(x_{\alpha })_{\alpha \in {\mathbb {N}}^{(m)}}$
be an
$(x_{\alpha })_{\alpha \in {\mathbb {N}}^{(m)}}$
be an
![]() ${\mathbb {N}}^{(m)}$
-sequence in a compact metric space
${\mathbb {N}}^{(m)}$
-sequence in a compact metric space
![]() $(X,d)$
. The above-introduced
$(X,d)$
. The above-introduced
![]() $\mathcal R$
-limits have an intrinsic connection with iterated limits of the form
$\mathcal R$
-limits have an intrinsic connection with iterated limits of the form
The goal of this extended remark is to clarify this connection.
-
(a) Using the compactness of X, one can show with the help of a diagonalization argument that for any increasing sequence
 $(k_j)_{j\in {\mathbb {N}}}$
, there exists a subsequence
$(k_j)_{j\in {\mathbb {N}}}$
, there exists a subsequence
 $(k_j')_{j\in {\mathbb {N}}}$
for which all the limits in (1.16) exist.
$(k_j')_{j\in {\mathbb {N}}}$
for which all the limits in (1.16) exist. -
(b) By Theorem 1.16, there exists an increasing sequence of natural numbers
 $(k_j)_{j\in {\mathbb {N}}}$
so that, for
$(k_j)_{j\in {\mathbb {N}}}$
so that, for
 $S=\{k_j\,|\,j\in {\mathbb {N}}\}$
,
$S=\{k_j\,|\,j\in {\mathbb {N}}\}$
,
 ${\mathop { \mathcal {R}{\text {-}\mathrm {lim}}}_{{\alpha \in S^{(m)}}}} x_{\alpha }$
exists. Let
${\mathop { \mathcal {R}{\text {-}\mathrm {lim}}}_{{\alpha \in S^{(m)}}}} x_{\alpha }$
exists. Let
 $(k_j')_{j\in {\mathbb {N}}}$
be the subsequence of
$(k_j')_{j\in {\mathbb {N}}}$
be the subsequence of
 $(k_j)_{j\in {\mathbb {N}}}$
which is guaranteed to exist by (a). Letting
$(k_j)_{j\in {\mathbb {N}}}$
which is guaranteed to exist by (a). Letting
 $S_1=\{k_j'\,|\,j\in {\mathbb {N}}\}$
, we have (1.17)
$S_1=\{k_j'\,|\,j\in {\mathbb {N}}\}$
, we have (1.17) $$ \begin{align} {\mathop { \mathcal {R}{\text{-}\mathrm{lim}}}_{{\alpha\in S_1^{(m)}}}}\ x_{\alpha}=\lim_{j_1\rightarrow\infty}\cdots\lim_{j_m\rightarrow\infty}x_{\{k^{\prime}_{j_1},\ldots,k^{\prime}_{j_m}\}}. \end{align} $$
$$ \begin{align} {\mathop { \mathcal {R}{\text{-}\mathrm{lim}}}_{{\alpha\in S_1^{(m)}}}}\ x_{\alpha}=\lim_{j_1\rightarrow\infty}\cdots\lim_{j_m\rightarrow\infty}x_{\{k^{\prime}_{j_1},\ldots,k^{\prime}_{j_m}\}}. \end{align} $$
-
(c) When
 $X=\{1,\ldots ,r\}$
, one can use (a) to prove Theorem 1.13. Let
$X=\{1,\ldots ,r\}$
, one can use (a) to prove Theorem 1.13. Let
 $r,m\in {\mathbb {N}}$
and consider a partition
$r,m\in {\mathbb {N}}$
and consider a partition
 ${\mathbb {N}}^{(m)}=\bigcup _{j=1}^r C_j$
. Let
${\mathbb {N}}^{(m)}=\bigcup _{j=1}^r C_j$
. Let
 $(x_{\alpha })_{\alpha \in {\mathbb {N}}^{(m)}}$
be defined by
$(x_{\alpha })_{\alpha \in {\mathbb {N}}^{(m)}}$
be defined by
 $x_{\alpha }=j$
if
$x_{\alpha }=j$
if
 $\alpha \in C_j$
. For some increasing sequence
$\alpha \in C_j$
. For some increasing sequence
 $(k_j)_{j\in {\mathbb {N}}}$
in
$(k_j)_{j\in {\mathbb {N}}}$
in
 ${\mathbb {N}}$
there exists a
${\mathbb {N}}$
there exists a
 $j_0\in \{1,\ldots ,r\}$
such that By using a diagonalization argument, we obtain a subsequence
$j_0\in \{1,\ldots ,r\}$
such that By using a diagonalization argument, we obtain a subsequence $$ \begin{align*} \lim_{j_1\rightarrow\infty}\cdots\lim_{j_m\rightarrow\infty}x_{\{k_{j_1},\ldots,k_{j_m}\}}=j_0. \end{align*} $$
$$ \begin{align*} \lim_{j_1\rightarrow\infty}\cdots\lim_{j_m\rightarrow\infty}x_{\{k_{j_1},\ldots,k_{j_m}\}}=j_0. \end{align*} $$
 $(k_j')_{j\in {\mathbb {N}}}$
of
$(k_j')_{j\in {\mathbb {N}}}$
of
 $(k_j)_{j\in {\mathbb {N}}}$
with the property that
$(k_j)_{j\in {\mathbb {N}}}$
with the property that
 $x_{\{k_{j_1}',\ldots ,k_{j_m}'\}}=j_0$
for any
$x_{\{k_{j_1}',\ldots ,k_{j_m}'\}}=j_0$
for any
 $j_1<\cdots <j_m$
. Now let
$j_1<\cdots <j_m$
. Now let
 $S=\{k_j'\,|\, j\in {\mathbb {N}}\}$
. It follows that
$S=\{k_j'\,|\, j\in {\mathbb {N}}\}$
. It follows that
 $S^{(m)}\subseteq C_{j_0}$
.
$S^{(m)}\subseteq C_{j_0}$
.
Before formulating our main result, we need two more definitions.
Definition 1.18. Let
![]() $m\in {\mathbb {N}}$
and let
$m\in {\mathbb {N}}$
and let
![]() $(G,+)$
be a countable abelian group. For any sequence
$(G,+)$
be a countable abelian group. For any sequence
![]() $(\textbf g_k)_{k\in {\mathbb {N}}}=(g_{k,1},\ldots ,g_{k,m})_{k\in {\mathbb {N}}}$
and any
$(\textbf g_k)_{k\in {\mathbb {N}}}=(g_{k,1},\ldots ,g_{k,m})_{k\in {\mathbb {N}}}$
and any
![]() $\alpha =\{k_1,\ldots ,k_m\}\in {\mathbb {N}}^{(m)}$
we let
$\alpha =\{k_1,\ldots ,k_m\}\in {\mathbb {N}}^{(m)}$
we let
 $$ \begin{align} g_{\alpha}=\sum_{j=1}^m g_{k_j,j}=g_{k_1,1}+g_{k_2,2}+\cdots+g_{k_m,m}, \end{align} $$
$$ \begin{align} g_{\alpha}=\sum_{j=1}^m g_{k_j,j}=g_{k_1,1}+g_{k_2,2}+\cdots+g_{k_m,m}, \end{align} $$
where
![]() $k_1<\cdots <k_m$
.
$k_1<\cdots <k_m$
.
Definition 1.19. Let
![]() $m\in {\mathbb {N}}$
, let
$m\in {\mathbb {N}}$
, let
![]() $(G,+)$
be a countable abelian group and let
$(G,+)$
be a countable abelian group and let
be sequences in
![]() $G^m$
. We say that
$G^m$
. We say that
![]() $(\textbf g_k)_{k\in {\mathbb {N}}}$
and
$(\textbf g_k)_{k\in {\mathbb {N}}}$
and
![]() $(\textbf h_k)_{k\in {\mathbb {N}}}$
are essentially distinct if, for each
$(\textbf h_k)_{k\in {\mathbb {N}}}$
are essentially distinct if, for each
![]() $t\in \{1,\ldots ,m\}$
,
$t\in \{1,\ldots ,m\}$
,
![]() $(g_{k,t})_{k\in {\mathbb {N}}}$
and
$(g_{k,t})_{k\in {\mathbb {N}}}$
and
![]() $(h_{k,t})_{k\in {\mathbb {N}}}$
grow apart (that is,
$(h_{k,t})_{k\in {\mathbb {N}}}$
grow apart (that is,
![]() $\lim _{k\rightarrow \infty }(g_{k,t}-h_{k,t})=\infty $
).
$\lim _{k\rightarrow \infty }(g_{k,t}-h_{k,t})=\infty $
).
Remark 1.20. The following observation indicates the natural connection between non-degenerated, essentially distinct sequences in
![]() $G^m$
and
$G^m$
and
![]() $\tilde {\Sigma }_m$
sets. Let
$\tilde {\Sigma }_m$
sets. Let
![]() $d,m\in {\mathbb {N}}$
and let
$d,m\in {\mathbb {N}}$
and let
![]() $(G,+)$
be a countable abelian group. Then for any non-degenerated and essentially distinct sequences
$(G,+)$
be a countable abelian group. Then for any non-degenerated and essentially distinct sequences
in
![]() $G^m$
, the set
$G^m$
, the set
 $$ \begin{align*} &\{(g_{\alpha}^{(1)},\ldots,g_{\alpha}^{(d)})\,|\,\alpha\in{\mathbb{N}}^{(m)}\}\\ &\quad=\{(g^{(1)}_{k_1,1}+\cdots+g^{(1)}_{k_m,m},\ldots,g^{(d)}_{k_1,1}+\cdots+g^{(d)}_{k_m,m})\,|\,k_1<\cdots<k_m\}\\ &\quad=\{(g^{(1)}_{k_1,1},\ldots,g^{(d)}_{k_1,1})+\cdots+(g^{(1)}_{k_m,m},\ldots,g^{(d)}_{k_m,m})\,|\,k_1<\cdots<k_m\} \end{align*} $$
$$ \begin{align*} &\{(g_{\alpha}^{(1)},\ldots,g_{\alpha}^{(d)})\,|\,\alpha\in{\mathbb{N}}^{(m)}\}\\ &\quad=\{(g^{(1)}_{k_1,1}+\cdots+g^{(1)}_{k_m,m},\ldots,g^{(d)}_{k_1,1}+\cdots+g^{(d)}_{k_m,m})\,|\,k_1<\cdots<k_m\}\\ &\quad=\{(g^{(1)}_{k_1,1},\ldots,g^{(d)}_{k_1,1})+\cdots+(g^{(1)}_{k_m,m},\ldots,g^{(d)}_{k_m,m})\,|\,k_1<\cdots<k_m\} \end{align*} $$
is a
![]() $\tilde {\Sigma }_m$
set in
$\tilde {\Sigma }_m$
set in
![]() $G^d$
.
$G^d$
.
We are now ready to formulate our main result (it appears as Theorem 3.1 in §3). It incorporates some of the characterizations of strongly mixing systems which were mentioned above.
Theorem 1.21. Let
![]() $\ell \in {\mathbb {N}}$
, let
$\ell \in {\mathbb {N}}$
, let
![]() $(G,+)$
be a countable abelian group and let
$(G,+)$
be a countable abelian group and let
![]() $(X,\mathcal A,\mu , (T_g)_{g\in G})$
be a measure-preserving system. The following statements are equivalent.
$(X,\mathcal A,\mu , (T_g)_{g\in G})$
be a measure-preserving system. The following statements are equivalent.
-
(i)
 $(T_g)_{g\in G}$
is strongly mixing.
$(T_g)_{g\in G}$
is strongly mixing. -
(ii) For any non-degenerated and essentially distinct sequences
in $$ \begin{align*}(\textbf g_k^{(j)})_{k\in{\mathbb{N}}}, \quad j\in\{1,\ldots,\ell\},\end{align*} $$
$$ \begin{align*}(\textbf g_k^{(j)})_{k\in{\mathbb{N}}}, \quad j\in\{1,\ldots,\ell\},\end{align*} $$
 $G^{(\ell )}$
, there exists an infinite
$G^{(\ell )}$
, there exists an infinite
 $S\subseteq {\mathbb {N}}$
such that, for any
$S\subseteq {\mathbb {N}}$
such that, for any
 $A_0,\ldots ,A_{\ell }\in \mathcal A$
, (1.19)
$A_0,\ldots ,A_{\ell }\in \mathcal A$
, (1.19) $$ \begin{align} {\mathop { \mathcal {R}{\text{-}\mathrm{lim}}}_{{\alpha\in S^{(\ell)}}}}\, \mu(A_0\cap T_{ g^{(1)}_{\alpha}}A_1\cap \cdots\cap T_{ g^{(\ell)}_{\alpha}}A_{\ell})=\prod_{j=0}^{\ell}\mu(A_j). \end{align} $$
$$ \begin{align} {\mathop { \mathcal {R}{\text{-}\mathrm{lim}}}_{{\alpha\in S^{(\ell)}}}}\, \mu(A_0\cap T_{ g^{(1)}_{\alpha}}A_1\cap \cdots\cap T_{ g^{(\ell)}_{\alpha}}A_{\ell})=\prod_{j=0}^{\ell}\mu(A_j). \end{align} $$
More explicitly, if
for each $$ \begin{align*} (\textbf g^{(j)}_k)_{k\in{\mathbb{N}}}=(g^{(j)}_{k,1},\ldots,g^{(j)}_{k,\ell})_{k\in{\mathbb{N}}}, \end{align*} $$
$$ \begin{align*} (\textbf g^{(j)}_k)_{k\in{\mathbb{N}}}=(g^{(j)}_{k,1},\ldots,g^{(j)}_{k,\ell})_{k\in{\mathbb{N}}}, \end{align*} $$
 $j\in \{1,\ldots ,\ell \},$
then
$j\in \{1,\ldots ,\ell \},$
then  $$ \begin{align*} {\mathop { \mathcal {R}{\text{-}\mathrm{lim}}}_{{\{k_1,\ldots,k_{\ell}\}\in S^{(\ell)}}}} \mu(A_0\cap T_{ g_{k_1,1}^{(1)}+\cdots+ g_{k_{\ell},\ell}^{(1)}}A_1\cap\cdots\cap T_{ g_{k_1,1}^{(\ell)}+\cdots+ g_{k_{\ell},\ell}^{(\ell)}}A_{\ell})=\prod_{j=0}^{\ell} \mu(A_j). \end{align*} $$
$$ \begin{align*} {\mathop { \mathcal {R}{\text{-}\mathrm{lim}}}_{{\{k_1,\ldots,k_{\ell}\}\in S^{(\ell)}}}} \mu(A_0\cap T_{ g_{k_1,1}^{(1)}+\cdots+ g_{k_{\ell},\ell}^{(1)}}A_1\cap\cdots\cap T_{ g_{k_1,1}^{(\ell)}+\cdots+ g_{k_{\ell},\ell}^{(\ell)}}A_{\ell})=\prod_{j=0}^{\ell} \mu(A_j). \end{align*} $$
-
(iii) For any
 $\epsilon>0$
and any
$\epsilon>0$
and any
 $A_0,\ldots ,A_{\ell }\in \mathcal A$
, the set is
$A_0,\ldots ,A_{\ell }\in \mathcal A$
, the set is $$ \begin{align*} &R_{\epsilon}(A_0,\ldots,A_{\ell})\\&\quad=\bigg\{(g_1,\ldots,g_{\ell})\in G^{\ell}\,\bigg|\,\,\bigg|\mu(A_0\cap T_{g_1}A_1\cap\cdots \cap T_{g_{\ell}}A_{\ell})-\prod_{j=0}^{\ell} \mu( A_j)\bigg|<\epsilon\bigg\} \end{align*} $$
$$ \begin{align*} &R_{\epsilon}(A_0,\ldots,A_{\ell})\\&\quad=\bigg\{(g_1,\ldots,g_{\ell})\in G^{\ell}\,\bigg|\,\,\bigg|\mu(A_0\cap T_{g_1}A_1\cap\cdots \cap T_{g_{\ell}}A_{\ell})-\prod_{j=0}^{\ell} \mu( A_j)\bigg|<\epsilon\bigg\} \end{align*} $$
 $\tilde \Sigma _{\ell }^*$
in
$\tilde \Sigma _{\ell }^*$
in
 $G^{\ell }$
.
$G^{\ell }$
.
-
(iv) For any
 $\epsilon>0$
and any
$\epsilon>0$
and any
 $A_0,A_1\in \mathcal A$
, the set
$A_0,A_1\in \mathcal A$
, the set
 $R_{\epsilon }(A_0,A_1)$
is
$R_{\epsilon }(A_0,A_1)$
is
 $\Sigma _{\ell }^*$
in G.
$\Sigma _{\ell }^*$
in G.
The structure of this paper is as follows. In §2 we review some basic facts about couplings of probability spaces and establish some auxiliary results which will be needed in §3 and §6. In §3 we prove our main result, Theorem 1.21 (=Theorem 3.1). In §4 we derive some diagonal results for strongly mixing systems. In §5 we describe the largeness properties of
![]() $\tilde {\Sigma }_m^*$
sets and, more specifically, of the sets
$\tilde {\Sigma }_m^*$
sets and, more specifically, of the sets
![]() $R_{\epsilon }(A_0,\ldots ,A_{\ell })$
. We also juxtapose the properties of
$R_{\epsilon }(A_0,\ldots ,A_{\ell })$
. We also juxtapose the properties of
![]() $\tilde {\Sigma }_m^*$
sets with those of
$\tilde {\Sigma }_m^*$
sets with those of
![]() $\tilde {{\text {IP}}}^{\mathrm {*}}$
sets and sets of uniform density one which are characteristic, correspondingly, of mild and weak mixing. In §6 we utilize the methods developed in §2 and §5 to obtain analogues of Theorem 1.21 for mildly and weakly mixing systems.
$\tilde {{\text {IP}}}^{\mathrm {*}}$
sets and sets of uniform density one which are characteristic, correspondingly, of mild and weak mixing. In §6 we utilize the methods developed in §2 and §5 to obtain analogues of Theorem 1.21 for mildly and weakly mixing systems.
Remark 1.22. Throughout this paper, we will be tacitly assuming that the measure-preserving systems
![]() $(X,\mathcal A,\mu ,(T_g)_{g\in G})$
that we are working with are regular, meaning that the underlying probability space
$(X,\mathcal A,\mu ,(T_g)_{g\in G})$
that we are working with are regular, meaning that the underlying probability space
![]() $(X,\mathcal A,\mu )$
is regular (that is, X is a compact metric space and
$(X,\mathcal A,\mu )$
is regular (that is, X is a compact metric space and
![]() $\mathcal A=\text {Borel}(X)$
). Note that this assumption can be made without loss of generality since every separable measure-preserving system is equivalent to a regular one (see, for instance, [Reference Furstenberg14, Proposition 5.3]).
$\mathcal A=\text {Borel}(X)$
). Note that this assumption can be made without loss of generality since every separable measure-preserving system is equivalent to a regular one (see, for instance, [Reference Furstenberg14, Proposition 5.3]).
2 Some auxiliary facts involving couplings and
 $\mathcal R$
-limits
$\mathcal R$
-limits
In this section we review some basic facts about couplings of probability spaces and establish some auxiliary results which will be needed in §3 and §6.
Definition 2.1. Let
![]() $N\in {\mathbb {N}}$
. Given regular probability spaces
$N\in {\mathbb {N}}$
. Given regular probability spaces
![]() $\textbf X_j=(X_j,\mathcal A_j,\mu _j)$
,
$\textbf X_j=(X_j,\mathcal A_j,\mu _j)$
,
![]() $j\in \{1,\ldots ,N\}$
, a coupling of
$j\in \{1,\ldots ,N\}$
, a coupling of
![]() $\textbf X_1,\ldots ,\textbf X_N$
is a Borel probability measure
$\textbf X_1,\ldots ,\textbf X_N$
is a Borel probability measure
![]() $\unicode{x3bb} $
defined on the measurable space
$\unicode{x3bb} $
defined on the measurable space
 $$ \begin{align*} \bigg(\prod_{j=1}^NX_j,\bigotimes_{j=1}^N \mathcal A_j\bigg) \end{align*} $$
$$ \begin{align*} \bigg(\prod_{j=1}^NX_j,\bigotimes_{j=1}^N \mathcal A_j\bigg) \end{align*} $$
having the property that, for any
![]() $j\in \{1,\ldots ,N\}$
and any
$j\in \{1,\ldots ,N\}$
and any
![]() $A\in \mathcal A_j$
,
$A\in \mathcal A_j$
,
![]() $\unicode{x3bb} (\pi _j^{-1}(A))=\mu _j(A)$
, where
$\unicode{x3bb} (\pi _j^{-1}(A))=\mu _j(A)$
, where
![]() $\pi _j:\prod _{i=1}^NX_i\rightarrow X_j$
is the projection map onto the jth coordinate of
$\pi _j:\prod _{i=1}^NX_i\rightarrow X_j$
is the projection map onto the jth coordinate of
![]() $\prod _{j=1}^N X_j$
. (A coupling is just a joining of the trivial measure-preserving systems
$\prod _{j=1}^N X_j$
. (A coupling is just a joining of the trivial measure-preserving systems
![]() $(X_j,\mathcal A_j,\mu _j, \text {Id}_j)$
,
$(X_j,\mathcal A_j,\mu _j, \text {Id}_j)$
,
![]() $j\in \{1,\ldots ,N\}$
, where
$j\in \{1,\ldots ,N\}$
, where
![]() $\text {Id}_j:X_j\rightarrow X_j$
denotes the identity map on
$\text {Id}_j:X_j\rightarrow X_j$
denotes the identity map on
![]() $X_j$
.)
$X_j$
.)
We will let
![]() $\mathcal C(\textbf X_1,\ldots ,\textbf X_N)$
denote the set of all couplings of
$\mathcal C(\textbf X_1,\ldots ,\textbf X_N)$
denote the set of all couplings of
![]() $\textbf X_1,\ldots ,\textbf X_N$
.
$\textbf X_1,\ldots ,\textbf X_N$
.
![]() $\mathcal C(\textbf X_1,\ldots ,\textbf X_N)$
is a closed subspace of the set of all probability Borel measures on
$\mathcal C(\textbf X_1,\ldots ,\textbf X_N)$
is a closed subspace of the set of all probability Borel measures on
![]() $\prod _{j=1}^NX_j$
endowed with the
$\prod _{j=1}^NX_j$
endowed with the
![]() ${\text {weak-*}}$
topology. With this topology,
${\text {weak-*}}$
topology. With this topology,
![]() $\mathcal C(\textbf X_1,\ldots ,\textbf X_N)$
is a compact metrizable space. Given a sequence
$\mathcal C(\textbf X_1,\ldots ,\textbf X_N)$
is a compact metrizable space. Given a sequence
![]() $(\unicode{x3bb} _k)_{k\in {\mathbb {N}}}$
in
$(\unicode{x3bb} _k)_{k\in {\mathbb {N}}}$
in
![]() $\mathcal C(\textbf X_1,\ldots ,\textbf X_N)$
,
$\mathcal C(\textbf X_1,\ldots ,\textbf X_N)$
,
if and only if, for any
![]() $A_1\in \mathcal A_1,\ldots,$
$A_1\in \mathcal A_1,\ldots,$
![]() $A_N\in \mathcal A_N$
,
$A_N\in \mathcal A_N$
,
The following proposition follows immediately from the compactness of
![]() $\mathcal C(\textbf X_1,\ldots ,\textbf X_N)$
and Theorem 1.16.
$\mathcal C(\textbf X_1,\ldots ,\textbf X_N)$
and Theorem 1.16.
Proposition 2.2. Let
![]() $\textbf X_j=(X_j,\mathcal A_j,\mu _j)$
,
$\textbf X_j=(X_j,\mathcal A_j,\mu _j)$
,
![]() $j\in \{1,\ldots ,N\}$
, be regular probability spaces. For any
$j\in \{1,\ldots ,N\}$
, be regular probability spaces. For any
![]() $m\in {\mathbb {N}}$
, any infinite
$m\in {\mathbb {N}}$
, any infinite
![]() $S\subseteq {\mathbb {N}}$
and any
$S\subseteq {\mathbb {N}}$
and any
![]() ${\mathbb {N}}^{(m)}$
-sequence
${\mathbb {N}}^{(m)}$
-sequence
![]() $(\unicode{x3bb} _{\alpha })_{\alpha \in {\mathbb {N}}^{(m)}}$
in
$(\unicode{x3bb} _{\alpha })_{\alpha \in {\mathbb {N}}^{(m)}}$
in
![]() $\mathcal C(\textbf X_1,\ldots ,\textbf X_N)$
,
$\mathcal C(\textbf X_1,\ldots ,\textbf X_N)$
,
if and only if, for any
![]() $A_1\in \mathcal A_1,\ldots,$
$A_1\in \mathcal A_1,\ldots,$
![]() $A_N\in \mathcal A_N$
,
$A_N\in \mathcal A_N$
,
Our next goal is to establish a useful criterion for mixing of higher orders (Proposition 2.9). First, we need a definition and two lemmas.
Definition 2.3. Let
![]() $(Z,\mathcal D,\unicode{x3bb} )$
be a regular probability space and let, for each
$(Z,\mathcal D,\unicode{x3bb} )$
be a regular probability space and let, for each
![]() $k\in {\mathbb {N}}$
,
$k\in {\mathbb {N}}$
,
![]() $T_k:Z\rightarrow Z$
be a measure-preserving transformation. The sequence
$T_k:Z\rightarrow Z$
be a measure-preserving transformation. The sequence
![]() $(T_k)_{k\in {\mathbb {N}}}$
has the mixing property if, for every
$(T_k)_{k\in {\mathbb {N}}}$
has the mixing property if, for every
![]() $A_0,A_1\in \mathcal D$
,
$A_0,A_1\in \mathcal D$
,
Remark 2.4
-
(a) If each of the transformations
 $T_k$
,
$T_k$
,
 $k\in {\mathbb {N}}$
, is invertible,
$k\in {\mathbb {N}}$
, is invertible,
 $(T_k)_{k\in {\mathbb {N}}}$
has the mixing property if and only if
$(T_k)_{k\in {\mathbb {N}}}$
has the mixing property if and only if
 $(T_k^{-1})_{k\in {\mathbb {N}}}$
has the mixing property.
$(T_k^{-1})_{k\in {\mathbb {N}}}$
has the mixing property. -
(b)
 $(T_k)_{k\in {\mathbb {N}}}$
has the mixing property if and only if, for any
$(T_k)_{k\in {\mathbb {N}}}$
has the mixing property if and only if, for any
 $f,g\in L^2(\mu )$
,
$f,g\in L^2(\mu )$
,  $$ \begin{align*}\lim_{k\rightarrow\infty}\int_X fT_kg\,\text{d}\mu=\int_Xf\,\text{d}\mu\int_Xg\,\text{d}\mu.\end{align*} $$
$$ \begin{align*}\lim_{k\rightarrow\infty}\int_X fT_kg\,\text{d}\mu=\int_Xf\,\text{d}\mu\int_Xg\,\text{d}\mu.\end{align*} $$
Lemma 2.5. Let
![]() $\textbf X=(X,\mathcal A,\mu )$
and
$\textbf X=(X,\mathcal A,\mu )$
and
![]() $\textbf Y=(Y,\mathcal B,\nu )$
be regular probability spaces. For each
$\textbf Y=(Y,\mathcal B,\nu )$
be regular probability spaces. For each
![]() $k\in {\mathbb {N}}$
, let
$k\in {\mathbb {N}}$
, let
![]() $T_k:Y\rightarrow Y$
be a measure-preserving transformation, and assume that the sequence
$T_k:Y\rightarrow Y$
be a measure-preserving transformation, and assume that the sequence
![]() $(T_k)_{k\in {\mathbb {N}}}$
has the mixing property. Let
$(T_k)_{k\in {\mathbb {N}}}$
has the mixing property. Let
![]() $\unicode{x3bb} _0$
be a coupling of
$\unicode{x3bb} _0$
be a coupling of
![]() $\textbf X$
and
$\textbf X$
and
![]() $\textbf Y$
. Assume that
$\textbf Y$
. Assume that
![]() $\unicode{x3bb} $
is a probability measure on
$\unicode{x3bb} $
is a probability measure on
![]() $\mathcal A\otimes \mathcal B$
such that, for any
$\mathcal A\otimes \mathcal B$
such that, for any
![]() $A\in \mathcal A$
and
$A\in \mathcal A$
and
![]() $B\in \mathcal B$
, one has
$B\in \mathcal B$
, one has
Then
![]() $\unicode{x3bb} =\mu \otimes \nu $
.
$\unicode{x3bb} =\mu \otimes \nu $
.
Proof. Note that it suffices to show that, for any
![]() $A\in \mathcal A$
and
$A\in \mathcal A$
and
![]() $B\in \mathcal B$
,
$B\in \mathcal B$
,
Fix
![]() $A\in \mathcal A$
and
$A\in \mathcal A$
and
![]() $B\in \mathcal B$
. Since
$B\in \mathcal B$
. Since
![]() , we have by (2.1) that
, we have by (2.1) that

Note that
![]() and, if we regard
and, if we regard
![]() $\mathcal B$
as a sub-
$\mathcal B$
as a sub-
![]() $\sigma $
-algebra of
$\sigma $
-algebra of
![]() $\mathcal A\otimes \mathcal B$
,
$\mathcal A\otimes \mathcal B$
,
![]() $\unicode{x3bb} _0|_{\mathcal B}=\nu $
. The rightmost expression in (2.3) equals
$\unicode{x3bb} _0|_{\mathcal B}=\nu $
. The rightmost expression in (2.3) equals

where
![]() denotes the conditional expectation of
denotes the conditional expectation of
![]() with respect to
with respect to
![]() $\mathcal B$
.
$\mathcal B$
.
But
![]() $(T_k)_{k\in {\mathbb {N}}}$
has the mixing property, so the rightmost expression in (2.4) equals
$(T_k)_{k\in {\mathbb {N}}}$
has the mixing property, so the rightmost expression in (2.4) equals
By noting that
we have that (2.5) equals
![]() $\mu (A)\nu (B)$
.
$\mu (A)\nu (B)$
.
Lemma 2.6. Let
![]() $m\in {\mathbb {N}}$
, let
$m\in {\mathbb {N}}$
, let
![]() $(X,d)$
be a compact metric space, and let
$(X,d)$
be a compact metric space, and let
![]() $(x_{\alpha })_{\alpha \in {\mathbb {N}}^{(m+1)}}$
be an
$(x_{\alpha })_{\alpha \in {\mathbb {N}}^{(m+1)}}$
be an
![]() ${\mathbb {N}}^{(m+1)}$
-sequence in X. Assume that there exists an infinite
${\mathbb {N}}^{(m+1)}$
-sequence in X. Assume that there exists an infinite
![]() $S\subseteq {\mathbb {N}}$
with the following properties: (a) for some
$S\subseteq {\mathbb {N}}$
with the following properties: (a) for some
![]() $x\in X$
,
$x\in X$
,
![]() ${\mathop { \mathcal {R}{\text {-}\mathrm {lim}}}_{{\alpha \in S^{(m+1)}}}} x_{\alpha }=x$
; (b) for each
${\mathop { \mathcal {R}{\text {-}\mathrm {lim}}}_{{\alpha \in S^{(m+1)}}}} x_{\alpha }=x$
; (b) for each
![]() $k\in S$
, there exists
$k\in S$
, there exists
![]() $y_k\in X$
such that
$y_k\in X$
such that
Then
Proof. Let
![]() $\epsilon>0$
. Note that (1) there exists
$\epsilon>0$
. Note that (1) there exists
![]() $k_0\in S$
such that, for any
$k_0\in S$
such that, for any
![]() $\alpha \in S^{(m+1)}$
with
$\alpha \in S^{(m+1)}$
with
![]() $k_0\leq \min \alpha $
,
$k_0\leq \min \alpha $
,
![]() $d(x_{\alpha }, x)<{\epsilon }/{2}$
and (2) for any
$d(x_{\alpha }, x)<{\epsilon }/{2}$
and (2) for any
![]() $k\in S$
, there exists an
$k\in S$
, there exists an
![]() $\alpha _k\in S^{(m)}$
such that, for any
$\alpha _k\in S^{(m)}$
such that, for any
![]() $\alpha \in S^{(m)}$
with
$\alpha \in S^{(m)}$
with
![]() $\min \alpha>\max (\alpha _k\cup \{k\})$
,
$\min \alpha>\max (\alpha _k\cup \{k\})$
,
![]() $d(x_{\{k\}\cup \alpha },y_k)<{\epsilon }/{2}$
. It follows that, for any
$d(x_{\{k\}\cup \alpha },y_k)<{\epsilon }/{2}$
. It follows that, for any
![]() $k\in S$
with
$k\in S$
with
![]() $k\geq k_0$
and any
$k\geq k_0$
and any
![]() $\alpha \in S^{(m)}$
with
$\alpha \in S^{(m)}$
with
![]() $\min \alpha>\max (\alpha _k\cup \{k\})$
,
$\min \alpha>\max (\alpha _k\cup \{k\})$
,
![]() $d(y_k,x)<d(x_{\{k\}\cup \alpha },y_k)+d(x_{\{k\}\cup \alpha },x)<\epsilon $
. Since
$d(y_k,x)<d(x_{\{k\}\cup \alpha },y_k)+d(x_{\{k\}\cup \alpha },x)<\epsilon $
. Since
![]() $\epsilon>0$
was arbitrary,
$\epsilon>0$
was arbitrary,
Remark 2.7. Let
![]() $m\in {\mathbb {N}}$
and let
$m\in {\mathbb {N}}$
and let
![]() $(x_{\alpha })_{\alpha \in {\mathbb {N}}^{(m+1)}}$
be an
$(x_{\alpha })_{\alpha \in {\mathbb {N}}^{(m+1)}}$
be an
![]() ${\mathbb {N}}^{(m+1)}$
-sequence in a compact metric space X. By applying Theorem 1.16 first to the
${\mathbb {N}}^{(m+1)}$
-sequence in a compact metric space X. By applying Theorem 1.16 first to the
![]() ${\mathbb {N}}^{(m)}$
-sequence
${\mathbb {N}}^{(m)}$
-sequence
![]() $(\omega _{\alpha })_{\alpha \in {\mathbb {N}}^{(m)}}=((x_{\{k\}\cup \alpha })_{k\in {\mathbb {N}}})_{\alpha \in {\mathbb {N}}^{(m)}}$
in
$(\omega _{\alpha })_{\alpha \in {\mathbb {N}}^{(m)}}=((x_{\{k\}\cup \alpha })_{k\in {\mathbb {N}}})_{\alpha \in {\mathbb {N}}^{(m)}}$
in
![]() $X^{\mathbb {N}}$
(here
$X^{\mathbb {N}}$
(here
![]() $x_{\{k\}\cup \alpha }=x_0$
for some fixed
$x_{\{k\}\cup \alpha }=x_0$
for some fixed
![]() $x_0\in X$
, whenever
$x_0\in X$
, whenever
![]() $k\geq \min \alpha $
), and then to the
$k\geq \min \alpha $
), and then to the
![]() ${\mathbb {N}}^{(m+1)}$
-sequence
${\mathbb {N}}^{(m+1)}$
-sequence
![]() $(x_{\alpha })_{\alpha \in {\mathbb {N}}^{(m+1)}}$
, we obtain an infinite set
$(x_{\alpha })_{\alpha \in {\mathbb {N}}^{(m+1)}}$
, we obtain an infinite set
![]() $S\subseteq {\mathbb {N}}$
for which (a) and (b) in the statement of Lemma 2.6 hold. A similar reasoning shows that one can pick S to be a subset of any prescribed in advance infinite set
$S\subseteq {\mathbb {N}}$
for which (a) and (b) in the statement of Lemma 2.6 hold. A similar reasoning shows that one can pick S to be a subset of any prescribed in advance infinite set
![]() $S_1\subseteq {\mathbb {N}}$
.
$S_1\subseteq {\mathbb {N}}$
.
Remark 2.8. In Remark 1.17(c), we indicated how the utilization of iterated limits
leads to a proof of Ramsey’s theorem (Theorem 1.13). In this remark, we show that Lemma 2.6 and Remark 2.7 (which are corollaries of Ramsey’s Theorem) imply that, for any infinite set
![]() $S_1\subseteq {\mathbb {N}}$
and any
$S_1\subseteq {\mathbb {N}}$
and any
![]() ${\mathbb {N}}^{(m)}$
-sequence
${\mathbb {N}}^{(m)}$
-sequence
![]() $(x_{\alpha })_{\alpha \in {\mathbb {N}}^{(m)}}$
in a compact metric space X, there exists an increasing sequence
$(x_{\alpha })_{\alpha \in {\mathbb {N}}^{(m)}}$
in a compact metric space X, there exists an increasing sequence
![]() $(k_j)_{j\in {\mathbb {N}}}$
in
$(k_j)_{j\in {\mathbb {N}}}$
in
![]() $S_1$
such that, for
$S_1$
such that, for
![]() $S=\{k_j\,|\,j\in {\mathbb {N}}\}$
, each of the limits in the formula
$S=\{k_j\,|\,j\in {\mathbb {N}}\}$
, each of the limits in the formula
exists. The proof is by induction on
![]() $m\in {\mathbb {N}}$
. When
$m\in {\mathbb {N}}$
. When
![]() $m=1$
, the result follows from the compactness of X. Now let
$m=1$
, the result follows from the compactness of X. Now let
![]() $m>1$
and let
$m>1$
and let
![]() $S_1$
be an infinite subset of
$S_1$
be an infinite subset of
![]() ${\mathbb {N}}$
. By Remark 2.7 and Lemma 2.6, there exists an increasing sequence
${\mathbb {N}}$
. By Remark 2.7 and Lemma 2.6, there exists an increasing sequence
![]() $(k_j)_{j\in {\mathbb {N}}}$
in
$(k_j)_{j\in {\mathbb {N}}}$
in
![]() $S_1$
such that, for
$S_1$
such that, for
![]() $S=\{k_j\,|\,j\in {\mathbb {N}}\}$
,
$S=\{k_j\,|\,j\in {\mathbb {N}}\}$
,
The result now follows from the inductive hypothesis applied to the infinite set
![]() $S\subseteq {\mathbb {N}}$
and the
$S\subseteq {\mathbb {N}}$
and the
![]() ${\mathbb {N}}^{(m-1)}$
-sequence
${\mathbb {N}}^{(m-1)}$
-sequence
![]() $((x_{\{k\}\cup \alpha })_{k\in {\mathbb {N}}})_{\alpha \in {\mathbb {N}}^{(m-1)}}$
in the compact metric space
$((x_{\{k\}\cup \alpha })_{k\in {\mathbb {N}}})_{\alpha \in {\mathbb {N}}^{(m-1)}}$
in the compact metric space
![]() $X^{\mathbb {N}}$
.
$X^{\mathbb {N}}$
.
The following proposition provides a useful technical tool for establishing higher-order mixing properties of measure-preserving systems. It will be instrumental in §3 for dealing with strongly mixing systems and in §6 where we will focus on mildly and weakly mixing systems.
Proposition 2.9. Let
![]() $(G,+)$
be a countable abelian group, let
$(G,+)$
be a countable abelian group, let
![]() $(X,\mathcal A,\mu , (T_g)_{g\in G})$
be a measure-preserving system, let
$(X,\mathcal A,\mu , (T_g)_{g\in G})$
be a measure-preserving system, let
![]() $\ell \in {\mathbb {N}}$
and, for each
$\ell \in {\mathbb {N}}$
and, for each
![]() $j\in \{1,\ldots ,\ell \}$
, let
$j\in \{1,\ldots ,\ell \}$
, let
be a sequence in
![]() $G^{\ell }$
. Suppose that, for any
$G^{\ell }$
. Suppose that, for any
![]() $t\in \{1,\ldots ,\ell \}$
and any
$t\in \{1,\ldots ,\ell \}$
and any
![]() $j\in \{1,\ldots ,\ell \}$
,
$j\in \{1,\ldots ,\ell \}$
,
![]() $(T_{g_{k,t}^{(j)}})_{k\in {\mathbb {N}}}$
has the mixing property and that, for any t and any
$(T_{g_{k,t}^{(j)}})_{k\in {\mathbb {N}}}$
has the mixing property and that, for any t and any
![]() $i\neq j$
,
$i\neq j$
,
![]() $(T_{(g_{k,t}^{(j)}-g_{k,t}^{(i)})})_{k\in {\mathbb {N}}}$
also has the mixing property. Then, there exists an infinite set
$(T_{(g_{k,t}^{(j)}-g_{k,t}^{(i)})})_{k\in {\mathbb {N}}}$
also has the mixing property. Then, there exists an infinite set
![]() $S\subseteq {\mathbb {N}}$
such that, for any
$S\subseteq {\mathbb {N}}$
such that, for any
![]() $A_0,\ldots ,A_{\ell }\in \mathcal A$
,
$A_0,\ldots ,A_{\ell }\in \mathcal A$
,
 $$ \begin{align*}{\mathop { \mathcal {R}{\text{-}\mathrm{lim}}}_{{\alpha\in S^{(\ell)}}}} \,\mu(A_0\cap T_{g^{(1)}_{\alpha}}A_1\cap\cdots\cap T_{g^{(\ell)}_{\alpha}}A_{\ell})=\prod_{j=0}^{\ell} \mu(A_j).\end{align*} $$
$$ \begin{align*}{\mathop { \mathcal {R}{\text{-}\mathrm{lim}}}_{{\alpha\in S^{(\ell)}}}} \,\mu(A_0\cap T_{g^{(1)}_{\alpha}}A_1\cap\cdots\cap T_{g^{(\ell)}_{\alpha}}A_{\ell})=\prod_{j=0}^{\ell} \mu(A_j).\end{align*} $$
Proof. The proof is by induction on
![]() $\ell $
. When
$\ell $
. When
![]() $\ell =1$
, it follows from our hypothesis that, for any
$\ell =1$
, it follows from our hypothesis that, for any
![]() $A_0,A_1\in \mathcal A$
,
$A_0,A_1\in \mathcal A$
,
Now fix
![]() $\ell \in {\mathbb {N}}$
and suppose that Proposition 2.9 holds for any
$\ell \in {\mathbb {N}}$
and suppose that Proposition 2.9 holds for any
![]() $\ell '\leq \ell $
. Let
$\ell '\leq \ell $
. Let
![]() $\textbf X=(X,\mathcal A,\mu )$
and let
$\textbf X=(X,\mathcal A,\mu )$
and let
![]() $\mu _{\Delta }\in \mathcal C=\mathcal C(\underbrace {\textbf X,\ldots , \textbf X}_{\ell +2\text { times}})$
be defined by
$\mu _{\Delta }\in \mathcal C=\mathcal C(\underbrace {\textbf X,\ldots , \textbf X}_{\ell +2\text { times}})$
be defined by
![]() $\mu (A_0\times \cdots \times A_{\ell +1})=\mu (A_0\cap \cdots \cap A_{\ell +1})$
. By the inductive hypothesis, there exists an infinite
$\mu (A_0\times \cdots \times A_{\ell +1})=\mu (A_0\cap \cdots \cap A_{\ell +1})$
. By the inductive hypothesis, there exists an infinite
![]() $S\subseteq {\mathbb {N}}$
such that, for any
$S\subseteq {\mathbb {N}}$
such that, for any
![]() $A_1,\ldots ,A_{\ell +1}\in \mathcal A$
,
$A_1,\ldots ,A_{\ell +1}\in \mathcal A$
,
 $$ \begin{align} &{\mathop { \mathcal {R}{\text{-}\mathrm{lim}}}_{{\{j_1,\ldots,j_{\ell}\}\in S^{(\ell)}}}} \mu_{\Delta}(X\times T_{g_{j_1,2}^{(1)}+\cdots+g_{j_{\ell},\ell+1}^{(1)}}A_1\times\cdots\times T_{g_{j_1,2}^{(\ell+1)}+\cdots+g_{j_{\ell},\ell+1}^{(\ell+1)}}A_{\ell+1})\nonumber\\ &\qquad={\mathop { \mathcal {R}{\text{-}\mathrm{lim}}}_{{\{j_1,\ldots,j_{\ell}\}\in S^{(\ell)}}}} \mu(X\cap T_{g_{j_1,2}^{(1)}+\cdots+g_{j_{\ell},\ell+1}^{(1)}}A_1\cap\cdots\cap T_{g_{j_1,2}^{(\ell+1)}+\cdots+g_{j_{\ell},\ell+1}^{(\ell+1)}}A_{\ell+1})\nonumber\\ &\qquad={\mathop { \mathcal {R}{\text{-}\mathrm{lim}}}_{{\{j_1,\ldots,j_{\ell}\}\in S^{(\ell)}}}} \mu( T_{g_{j_1,2}^{(1)}+\cdots+g_{j_{\ell},\ell+1}^{(1)}}A_1\cap\cdots\cap T_{g_{j_1,2}^{(\ell+1)}+\cdots+g_{j_{\ell},\ell+1}^{(\ell+1)}}A_{\ell+1})\nonumber\\ &\qquad={\mathop { \mathcal {R}{\text{-}\mathrm{lim}}}_{{\{j_1,\ldots,j_{\ell}\}\in S^{(\ell)}}}} \mu(A_1\cap T_{(g_{j_{1},2}^{(2)}-g_{j_{1},2}^{(1)})+\cdots+(g_{j_{\ell},\ell+1}^{(2)}-g_{j_{\ell},\ell+1}^{(1)})}\nonumber\\ &\quad\qquad A_2\cap\cdots\cap T_{(g_{j_1,2}^{(\ell+1)}-g_{j_{1},2}^{(1)})+\cdots+(g_{j_{\ell},\ell+1}^{(\ell+1)}-g_{j_{\ell},\ell+1}^{(1)})}A_{\ell+1})\nonumber\\ &\qquad=\prod_{j=1}^{\ell+1}\mu(A_j). \end{align} $$
$$ \begin{align} &{\mathop { \mathcal {R}{\text{-}\mathrm{lim}}}_{{\{j_1,\ldots,j_{\ell}\}\in S^{(\ell)}}}} \mu_{\Delta}(X\times T_{g_{j_1,2}^{(1)}+\cdots+g_{j_{\ell},\ell+1}^{(1)}}A_1\times\cdots\times T_{g_{j_1,2}^{(\ell+1)}+\cdots+g_{j_{\ell},\ell+1}^{(\ell+1)}}A_{\ell+1})\nonumber\\ &\qquad={\mathop { \mathcal {R}{\text{-}\mathrm{lim}}}_{{\{j_1,\ldots,j_{\ell}\}\in S^{(\ell)}}}} \mu(X\cap T_{g_{j_1,2}^{(1)}+\cdots+g_{j_{\ell},\ell+1}^{(1)}}A_1\cap\cdots\cap T_{g_{j_1,2}^{(\ell+1)}+\cdots+g_{j_{\ell},\ell+1}^{(\ell+1)}}A_{\ell+1})\nonumber\\ &\qquad={\mathop { \mathcal {R}{\text{-}\mathrm{lim}}}_{{\{j_1,\ldots,j_{\ell}\}\in S^{(\ell)}}}} \mu( T_{g_{j_1,2}^{(1)}+\cdots+g_{j_{\ell},\ell+1}^{(1)}}A_1\cap\cdots\cap T_{g_{j_1,2}^{(\ell+1)}+\cdots+g_{j_{\ell},\ell+1}^{(\ell+1)}}A_{\ell+1})\nonumber\\ &\qquad={\mathop { \mathcal {R}{\text{-}\mathrm{lim}}}_{{\{j_1,\ldots,j_{\ell}\}\in S^{(\ell)}}}} \mu(A_1\cap T_{(g_{j_{1},2}^{(2)}-g_{j_{1},2}^{(1)})+\cdots+(g_{j_{\ell},\ell+1}^{(2)}-g_{j_{\ell},\ell+1}^{(1)})}\nonumber\\ &\quad\qquad A_2\cap\cdots\cap T_{(g_{j_1,2}^{(\ell+1)}-g_{j_{1},2}^{(1)})+\cdots+(g_{j_{\ell},\ell+1}^{(\ell+1)}-g_{j_{\ell},\ell+1}^{(1)})}A_{\ell+1})\nonumber\\ &\qquad=\prod_{j=1}^{\ell+1}\mu(A_j). \end{align} $$
By Theorem 1.16 and the compactness of
![]() $\mathcal C$
, there exist an infinite set
$\mathcal C$
, there exist an infinite set
![]() $S_0\subseteq S$
and
$S_0\subseteq S$
and
![]() $\unicode{x3bb} _0\in \mathcal C$
such that, for any
$\unicode{x3bb} _0\in \mathcal C$
such that, for any
![]() $A_0,\ldots ,A_{\ell +1}\in \mathcal A$
,
$A_0,\ldots ,A_{\ell +1}\in \mathcal A$
,
 $$ \begin{align} {\mathop { \mathcal {R}{\text{-}\mathrm{lim}}}_{{\{j_1,\ldots,j_{\ell}\}\in S_0^{(\ell)}}}} \mu_{\Delta}(A_0\times T_{g_{j_1,2}^{(1)}+\cdots+g_{j_{\ell},\ell+1}^{(1)}}A_1\times\cdots\times T_{g_{j_1,2}^{(\ell+1)}+\cdots+g_{j_{\ell},\ell+1}^{(\ell+1)}}A_{\ell+1})=\unicode{x3bb}_0\bigg(\prod_{j=0}^{\ell+1}A_j\bigg). \end{align} $$
$$ \begin{align} {\mathop { \mathcal {R}{\text{-}\mathrm{lim}}}_{{\{j_1,\ldots,j_{\ell}\}\in S_0^{(\ell)}}}} \mu_{\Delta}(A_0\times T_{g_{j_1,2}^{(1)}+\cdots+g_{j_{\ell},\ell+1}^{(1)}}A_1\times\cdots\times T_{g_{j_1,2}^{(\ell+1)}+\cdots+g_{j_{\ell},\ell+1}^{(\ell+1)}}A_{\ell+1})=\unicode{x3bb}_0\bigg(\prod_{j=0}^{\ell+1}A_j\bigg). \end{align} $$
Likewise, there exist an infinite set
![]() $S_1\subseteq S_0$
and
$S_1\subseteq S_0$
and
![]() $\unicode{x3bb} \in \mathcal C$
such that, for any
$\unicode{x3bb} \in \mathcal C$
such that, for any
![]() $A_0,\ldots , A_{\ell +1}\in \mathcal A$
,
$A_0,\ldots , A_{\ell +1}\in \mathcal A$
,
 $$ \begin{align} &{\mathop { \mathcal {R}{\text{-}\mathrm{lim}}}_{{\{j_1,\ldots,j_{\ell+1}\}\in S_1^{(\ell+1)}}}} \mu_{\Delta}(A_0\times T_{g_{j_1,1}^{(1)}+\cdots+g_{j_{\ell+1},\ell+1}^{(1)}}A_1\times\cdots\times T_{g_{j_1,1}^{(\ell+1)}+\cdots+g_{j_{\ell+1},\ell+1}^{(\ell+1)}}A_{\ell+1})\nonumber\\ &\quad\qquad=\unicode{x3bb}\bigg(\prod_{j=0}^{\ell+1}A_j\bigg). \end{align} $$
$$ \begin{align} &{\mathop { \mathcal {R}{\text{-}\mathrm{lim}}}_{{\{j_1,\ldots,j_{\ell+1}\}\in S_1^{(\ell+1)}}}} \mu_{\Delta}(A_0\times T_{g_{j_1,1}^{(1)}+\cdots+g_{j_{\ell+1},\ell+1}^{(1)}}A_1\times\cdots\times T_{g_{j_1,1}^{(\ell+1)}+\cdots+g_{j_{\ell+1},\ell+1}^{(\ell+1)}}A_{\ell+1})\nonumber\\ &\quad\qquad=\unicode{x3bb}\bigg(\prod_{j=0}^{\ell+1}A_j\bigg). \end{align} $$
Let
![]() $\textbf {Y}=(\prod _{j=1}^{\ell +1} X,\bigotimes _{j=1}^{\ell +1}\mathcal A, \bigotimes _{j=1}^{\ell +1}\mu )$
. Note that (2.6) holds if we substitute
$\textbf {Y}=(\prod _{j=1}^{\ell +1} X,\bigotimes _{j=1}^{\ell +1}\mathcal A, \bigotimes _{j=1}^{\ell +1}\mu )$
. Note that (2.6) holds if we substitute
![]() $S_1$
for S and (2.7) holds when we substitute
$S_1$
for S and (2.7) holds when we substitute
![]() $S_1$
for
$S_1$
for
![]() $S_0$
. Performing this substitution and applying first (2.7) and then (2.6) to
$S_0$
. Performing this substitution and applying first (2.7) and then (2.6) to
![]() $A_1,\ldots ,A_{\ell +1}\in \mathcal A$
, we have
$A_1,\ldots ,A_{\ell +1}\in \mathcal A$
, we have
 $$ \begin{align*}\unicode{x3bb}_0(X\times A_1\times\cdots\times A_{\ell+1})=\prod_{j=1}^{\ell+1}\mu(A_{j}).\end{align*} $$
$$ \begin{align*}\unicode{x3bb}_0(X\times A_1\times\cdots\times A_{\ell+1})=\prod_{j=1}^{\ell+1}\mu(A_{j}).\end{align*} $$
Also, trivially, for any
![]() $A_0\in \mathcal A$
,
$A_0\in \mathcal A$
,
Thus,
![]() $\unicode{x3bb} _0$
is a coupling of
$\unicode{x3bb} _0$
is a coupling of
![]() $\textbf X$
and
$\textbf X$
and
![]() $\textbf Y$
.
$\textbf Y$
.
Using formula (2.7), Lemma 2.6 and applying (2.8) to the set
![]() $S_1=\{k_j\,|\,j\in {\mathbb {N}}\}$
(where we assume that
$S_1=\{k_j\,|\,j\in {\mathbb {N}}\}$
(where we assume that
![]() $(k_j)_{j\in {\mathbb {N}}}$
is an increasing sequence), we have
$(k_j)_{j\in {\mathbb {N}}}$
is an increasing sequence), we have
 $$ \begin{align} &\lim_{t\rightarrow\infty}\unicode{x3bb}_0(A_0\times T_{g_{k_{t},1}^{(1)}}A_1\times\cdots\times T_{g_{k_{t},1}^{(\ell+1)}}A_{\ell+1} )\nonumber\\ &\quad=\lim_{t\rightarrow\infty} {\mathop { \mathcal {R}{\text{-}\mathrm{lim}}}_{{\{j_2,\ldots,j_{\ell+1}\}\in S_1^{(\ell)}}}} \mu_{\Delta}(A_0\times T_{g_{j_2,2}^{(1)}+\cdots+g_{j_{\ell+1},\ell+1}^{(1)}}(T_{g_{k_{t},1}^{(1)}}A_1)\nonumber\\ &\quad\qquad\times\cdots\times T_{g_{j_2,2}^{(\ell+1)}+\cdots+g_{j_{\ell+1},\ell+1}^{(\ell+1)}}(T_{g_{k_{t},1}^{(\ell+1)}}A_{\ell+1}))\nonumber\\ &\quad=\lim_{t\rightarrow\infty} {\mathop { \mathcal {R}{\text{-}\mathrm{lim}}}_{{\{j_2,\ldots,j_{\ell+1}\}\in S_1^{(\ell)},\,k_t<j_2}}} \mu_{\Delta}(A_0\times T_{g_{k_{t},1}^{(1)}+g_{j_2,2}^{(1)}+\cdots+g_{j_{\ell+1},\ell+1}^{(1)}}A_1\nonumber\\ &\quad\qquad\times\cdots\times T_{g_{k_{t},1}^{(\ell+1)}+g_{j_2,2}^{(\ell+1)}+\cdots+g_{j_{\ell+1},\ell+1}^{(\ell+1)}}A_{\ell+1})\nonumber\\ &\quad={\mathop { \mathcal {R}{\text{-}\mathrm{lim}}}_{{\{j_1,\ldots,j_{\ell+1}\}\in S_1^{(\ell+1)}}}} \mu_{\Delta}(A_0\times T_{g_{j_1,1}^{(1)}+\cdots+g_{j_{\ell+1},\ell+1}^{(1)}}A_1\times\cdots\times T_{g_{j_1,1}^{(\ell+1)}+\cdots+g_{j_{\ell+1},\ell+1}^{(\ell+1)}}A_{\ell+1})\nonumber\\ &\quad=\unicode{x3bb}\bigg(\prod_{j=0}^{\ell+1}A_j\bigg), \end{align} $$
$$ \begin{align} &\lim_{t\rightarrow\infty}\unicode{x3bb}_0(A_0\times T_{g_{k_{t},1}^{(1)}}A_1\times\cdots\times T_{g_{k_{t},1}^{(\ell+1)}}A_{\ell+1} )\nonumber\\ &\quad=\lim_{t\rightarrow\infty} {\mathop { \mathcal {R}{\text{-}\mathrm{lim}}}_{{\{j_2,\ldots,j_{\ell+1}\}\in S_1^{(\ell)}}}} \mu_{\Delta}(A_0\times T_{g_{j_2,2}^{(1)}+\cdots+g_{j_{\ell+1},\ell+1}^{(1)}}(T_{g_{k_{t},1}^{(1)}}A_1)\nonumber\\ &\quad\qquad\times\cdots\times T_{g_{j_2,2}^{(\ell+1)}+\cdots+g_{j_{\ell+1},\ell+1}^{(\ell+1)}}(T_{g_{k_{t},1}^{(\ell+1)}}A_{\ell+1}))\nonumber\\ &\quad=\lim_{t\rightarrow\infty} {\mathop { \mathcal {R}{\text{-}\mathrm{lim}}}_{{\{j_2,\ldots,j_{\ell+1}\}\in S_1^{(\ell)},\,k_t<j_2}}} \mu_{\Delta}(A_0\times T_{g_{k_{t},1}^{(1)}+g_{j_2,2}^{(1)}+\cdots+g_{j_{\ell+1},\ell+1}^{(1)}}A_1\nonumber\\ &\quad\qquad\times\cdots\times T_{g_{k_{t},1}^{(\ell+1)}+g_{j_2,2}^{(\ell+1)}+\cdots+g_{j_{\ell+1},\ell+1}^{(\ell+1)}}A_{\ell+1})\nonumber\\ &\quad={\mathop { \mathcal {R}{\text{-}\mathrm{lim}}}_{{\{j_1,\ldots,j_{\ell+1}\}\in S_1^{(\ell+1)}}}} \mu_{\Delta}(A_0\times T_{g_{j_1,1}^{(1)}+\cdots+g_{j_{\ell+1},\ell+1}^{(1)}}A_1\times\cdots\times T_{g_{j_1,1}^{(\ell+1)}+\cdots+g_{j_{\ell+1},\ell+1}^{(\ell+1)}}A_{\ell+1})\nonumber\\ &\quad=\unicode{x3bb}\bigg(\prod_{j=0}^{\ell+1}A_j\bigg), \end{align} $$
For each
![]() $j\in {\mathbb {N}}$
, let
$j\in {\mathbb {N}}$
, let
![]() $\textbf T_j=T_{g_{k_j,1}^{(1)}}\times \cdots \times T_{g_{k_j,1}^{(\ell +1)}}$
. Note that, for any increasing sequence
$\textbf T_j=T_{g_{k_j,1}^{(1)}}\times \cdots \times T_{g_{k_j,1}^{(\ell +1)}}$
. Note that, for any increasing sequence
![]() $(t_s)_{s\in {\mathbb {N}}}$
in
$(t_s)_{s\in {\mathbb {N}}}$
in
![]() ${\mathbb {N}}$
, there exist a subsequence
${\mathbb {N}}$
, there exist a subsequence
![]() $(t^{\prime }_s)_{s\in {\mathbb {N}}}$
and a measure
$(t^{\prime }_s)_{s\in {\mathbb {N}}}$
and a measure
![]() $\unicode{x3bb} '\in \mathcal C(\textbf X,\textbf Y)$
, such that, for any
$\unicode{x3bb} '\in \mathcal C(\textbf X,\textbf Y)$
, such that, for any
![]() $A\in \mathcal A$
and any
$A\in \mathcal A$
and any
![]() $B\in \bigotimes _{j=1}^{\ell +1}\mathcal A$
,
$B\in \bigotimes _{j=1}^{\ell +1}\mathcal A$
,
![]() $\lim _{s\rightarrow \infty }\unicode{x3bb} _0(A\times \textbf T_{t^{\prime }_s}B)=\unicode{x3bb} '(A\times B)$
. By (2.9),
$\lim _{s\rightarrow \infty }\unicode{x3bb} _0(A\times \textbf T_{t^{\prime }_s}B)=\unicode{x3bb} '(A\times B)$
. By (2.9),
![]() $\unicode{x3bb} '=\unicode{x3bb} $
and hence, for any
$\unicode{x3bb} '=\unicode{x3bb} $
and hence, for any
![]() $A\in \mathcal A$
and any
$A\in \mathcal A$
and any
![]() $B\in \bigotimes _{j=1}^{\ell +1}\mathcal A$
,
$B\in \bigotimes _{j=1}^{\ell +1}\mathcal A$
,
![]() $\lim _{j\rightarrow \infty }\unicode{x3bb} _0(A\times \textbf T_j B)=\unicode{x3bb} (A\times B)$
.
$\lim _{j\rightarrow \infty }\unicode{x3bb} _0(A\times \textbf T_j B)=\unicode{x3bb} (A\times B)$
.
By Lemma 2.5 applied to
![]() $\textbf X=(X,\mathcal A,\mu )$
,
$\textbf X=(X,\mathcal A,\mu )$
,
![]() $\textbf Y=(\prod _{j=1}^{\ell +1} X,\bigotimes _{j=1}^{\ell +1}\mathcal A, \bigotimes _{j=1}^{\ell +1}\mu )$
and the sequence of measure-preserving transformations
$\textbf Y=(\prod _{j=1}^{\ell +1} X,\bigotimes _{j=1}^{\ell +1}\mathcal A, \bigotimes _{j=1}^{\ell +1}\mu )$
and the sequence of measure-preserving transformations
![]() $(T^{-1}_{g_{k_j,1}^{(1)}}\times \cdots \times T^{-1}_{g_{k_j,1}^{(\ell +1)}})_{j\in {\mathbb {N}}}$
, we have that
$(T^{-1}_{g_{k_j,1}^{(1)}}\times \cdots \times T^{-1}_{g_{k_j,1}^{(\ell +1)}})_{j\in {\mathbb {N}}}$
, we have that
![]() $\unicode{x3bb} =\bigotimes _{j=0}^{\ell +1}\mu $
. It follows that, for any
$\unicode{x3bb} =\bigotimes _{j=0}^{\ell +1}\mu $
. It follows that, for any
![]() $A_0,\ldots ,A_{\ell +1}\in \mathcal A$
,
$A_0,\ldots ,A_{\ell +1}\in \mathcal A$
,
 $$ \begin{align*} &{\mathop { \mathcal {R}{\text{-}\mathrm{lim}}}_{{\alpha\in S_1^{(\ell+1)}}}} \mu(A_0\cap T_{g^{(1)}_{\alpha}}A_1\cap\cdots\cap T_{g^{(\ell+1)}_{\alpha}}A_{\ell+1})\\ &\quad={\mathop { \mathcal {R}{\text{-}\mathrm{lim}}}_{{\alpha\in S_1^{(\ell+1)}}}} \mu_{\Delta} (A_0\times T_{g^{(1)}_{\alpha}}A_1\times\cdots\times T_{g^{(\ell+1)}_{\alpha}}A_{\ell+1})=\prod_{j=0}^{\ell+1} \mu(A_j), \end{align*} $$
$$ \begin{align*} &{\mathop { \mathcal {R}{\text{-}\mathrm{lim}}}_{{\alpha\in S_1^{(\ell+1)}}}} \mu(A_0\cap T_{g^{(1)}_{\alpha}}A_1\cap\cdots\cap T_{g^{(\ell+1)}_{\alpha}}A_{\ell+1})\\ &\quad={\mathop { \mathcal {R}{\text{-}\mathrm{lim}}}_{{\alpha\in S_1^{(\ell+1)}}}} \mu_{\Delta} (A_0\times T_{g^{(1)}_{\alpha}}A_1\times\cdots\times T_{g^{(\ell+1)}_{\alpha}}A_{\ell+1})=\prod_{j=0}^{\ell+1} \mu(A_j), \end{align*} $$
completing the proof.
3 Strongly mixing systems are ‘almost’ strongly mixing of all orders
In this section we will prove the following theorem (Theorem 1.21 from the Introduction) which is the main result of this paper.
Theorem 3.1. Let
![]() $\ell \in {\mathbb {N}}$
and let
$\ell \in {\mathbb {N}}$
and let
![]() $(X,\mathcal A,\mu , (T_g)_{g\in G})$
be a measure-preserving system. The following statements are equivalent.
$(X,\mathcal A,\mu , (T_g)_{g\in G})$
be a measure-preserving system. The following statements are equivalent.
-
(i)
 $(T_g)_{g\in G}$
is strongly mixing.
$(T_g)_{g\in G}$
is strongly mixing. -
(ii) For any
 $\ell $
non-degenerated and essentially distinct sequences in
$\ell $
non-degenerated and essentially distinct sequences in $$ \begin{align*}(\textbf g_k^{(j)})_{k\in{\mathbb{N}}}=(g^{(j)}_{k,1},\ldots,g^{(j)}_{k,\ell})_{k\in{\mathbb{N}}},\text{ }j\in\{1,\ldots,\ell\},\end{align*} $$
$$ \begin{align*}(\textbf g_k^{(j)})_{k\in{\mathbb{N}}}=(g^{(j)}_{k,1},\ldots,g^{(j)}_{k,\ell})_{k\in{\mathbb{N}}},\text{ }j\in\{1,\ldots,\ell\},\end{align*} $$
 $G^{\ell }$
, there exists an infinite
$G^{\ell }$
, there exists an infinite
 $S\subseteq {\mathbb {N}}$
such that, for any
$S\subseteq {\mathbb {N}}$
such that, for any
 $A_0,\ldots ,A_{\ell }\in \mathcal A$
, (3.1)
$A_0,\ldots ,A_{\ell }\in \mathcal A$
, (3.1) $$ \begin{align} {\mathop { \mathcal {R}{\text{-}\mathrm{lim}}}_{{\alpha\in S^{(\ell)}}}}\, \mu(A_0\cap T_{ g^{(1)}_{\alpha}}A_1\cap \cdots\cap T_{ g^{(\ell)}_{\alpha}}A_{\ell})=\prod_{j=0}^{\ell}\mu(A_j). \end{align} $$
$$ \begin{align} {\mathop { \mathcal {R}{\text{-}\mathrm{lim}}}_{{\alpha\in S^{(\ell)}}}}\, \mu(A_0\cap T_{ g^{(1)}_{\alpha}}A_1\cap \cdots\cap T_{ g^{(\ell)}_{\alpha}}A_{\ell})=\prod_{j=0}^{\ell}\mu(A_j). \end{align} $$
-
(iii) For any
 $\epsilon>0$
and any
$\epsilon>0$
and any
 $A_0,\ldots ,A_{\ell }\in \mathcal A$
, the set is
$A_0,\ldots ,A_{\ell }\in \mathcal A$
, the set is $$ \begin{align*}&R_{\epsilon}(A_0,\ldots,A_{\ell})\\&\quad=\bigg\{(g_1,\ldots,g_{\ell})\in G^{\ell}\,\bigg|\,\,\bigg|\mu(A_0\cap T_{g_1}A_1\cap\cdots \cap T_{g_{\ell}}A_{\ell})-\prod_{j=0}^{\ell} \mu( A_j)\bigg|<\epsilon\bigg\}\end{align*} $$
$$ \begin{align*}&R_{\epsilon}(A_0,\ldots,A_{\ell})\\&\quad=\bigg\{(g_1,\ldots,g_{\ell})\in G^{\ell}\,\bigg|\,\,\bigg|\mu(A_0\cap T_{g_1}A_1\cap\cdots \cap T_{g_{\ell}}A_{\ell})-\prod_{j=0}^{\ell} \mu( A_j)\bigg|<\epsilon\bigg\}\end{align*} $$
 $\tilde \Sigma _{\ell }^*$
in
$\tilde \Sigma _{\ell }^*$
in
 $G^{\ell }$
.
$G^{\ell }$
.
-
(iv) For any
 $\epsilon>0$
and any
$\epsilon>0$
and any
 $A_0,A_1\in \mathcal A$
, the set
$A_0,A_1\in \mathcal A$
, the set
 $R_{\epsilon }(A_0,A_1)$
is
$R_{\epsilon }(A_0,A_1)$
is
 $\Sigma _{\ell }^*$
in G.
$\Sigma _{\ell }^*$
in G.
Proof. (i)
![]() $\implies $
(ii): Note that since
$\implies $
(ii): Note that since
![]() $(T_g)_{g\in G}$
is strongly mixing, for any
$(T_g)_{g\in G}$
is strongly mixing, for any
![]() $t\in \{1,\ldots ,\ell \}$
and any
$t\in \{1,\ldots ,\ell \}$
and any
![]() $j\in \{1,\ldots ,\ell \}$
,
$j\in \{1,\ldots ,\ell \}$
,
![]() $(T_{g_{k,t}^{(j)}})_{k\in {\mathbb {N}}}$
has the mixing property and that for any t and any
$(T_{g_{k,t}^{(j)}})_{k\in {\mathbb {N}}}$
has the mixing property and that for any t and any
![]() $i\neq j$
,
$i\neq j$
,
![]() $(T_{(g_{k,t}^{(j)}-g_{k,t}^{(i)})})_{k\in {\mathbb {N}}}$
also has the mixing property. Thus (ii) follows from Proposition 2.9.
$(T_{(g_{k,t}^{(j)}-g_{k,t}^{(i)})})_{k\in {\mathbb {N}}}$
also has the mixing property. Thus (ii) follows from Proposition 2.9.
(ii)
![]() $\implies $
(iii): By (ii), we have that, for any
$\implies $
(iii): By (ii), we have that, for any
![]() $\epsilon>0$
, any
$\epsilon>0$
, any
![]() $A_0,\ldots ,,A_{\ell }\in \mathcal A$
and any
$A_0,\ldots ,,A_{\ell }\in \mathcal A$
and any
![]() $\ell $
non-degenerated and essentially distinct sequences
$\ell $
non-degenerated and essentially distinct sequences
in
![]() $G^{\ell }$
, there exists an
$G^{\ell }$
, there exists an
![]() $\alpha \in {\mathbb {N}}^{(\ell )}$
such that
$\alpha \in {\mathbb {N}}^{(\ell )}$
such that
which implies that
![]() $R_{\epsilon }(A_0,\ldots ,A_{\ell })$
is
$R_{\epsilon }(A_0,\ldots ,A_{\ell })$
is
![]() $\tilde {\Sigma }_{\ell }^*$
.
$\tilde {\Sigma }_{\ell }^*$
.
(iii)
![]() $\implies $
(iv): Let
$\implies $
(iv): Let
![]() $\epsilon>0$
, let
$\epsilon>0$
, let
![]() $A_0,A_1\in \mathcal A$
and let
$A_0,A_1\in \mathcal A$
and let
![]() $(\textbf g^{(1)}_k)_{k\in {\mathbb {N}}}=(g_{k,1}^{(1)},\ldots ,g_{k,\ell }^{(1)})_{k\in {\mathbb {N}}}$
be a non-degenerated sequence in
$(\textbf g^{(1)}_k)_{k\in {\mathbb {N}}}=(g_{k,1}^{(1)},\ldots ,g_{k,\ell }^{(1)})_{k\in {\mathbb {N}}}$
be a non-degenerated sequence in
![]() $G^{\ell }$
. In order to prove that
$G^{\ell }$
. In order to prove that
![]() $\mathcal R_{\epsilon }(A_0,A_1)$
is
$\mathcal R_{\epsilon }(A_0,A_1)$
is
![]() $\Sigma _{\ell }^*$
, it suffices to show that for some
$\Sigma _{\ell }^*$
, it suffices to show that for some
![]() $\alpha \in {\mathbb {N}}^{(\ell )}$
,
$\alpha \in {\mathbb {N}}^{(\ell )}$
,
![]() $g_{\alpha }^{(1)}\in \mathcal R_{\epsilon }(A_0,A_1)$
.
$g_{\alpha }^{(1)}\in \mathcal R_{\epsilon }(A_0,A_1)$
.
Note that, for any sequence
![]() $(h^{(1)}_k)_{k\in {\mathbb {N}}}$
in G with
$(h^{(1)}_k)_{k\in {\mathbb {N}}}$
in G with
![]() $\lim _{k\rightarrow \infty }h_k^{(1)}=\infty $
, one can pick sequences
$\lim _{k\rightarrow \infty }h_k^{(1)}=\infty $
, one can pick sequences
![]() $(h^{(2)}_k)_{k\in {\mathbb {N}}},\ldots,$
$(h^{(2)}_k)_{k\in {\mathbb {N}}},\ldots,$
![]() $(h^{(\ell )}_k)_{k\in {\mathbb {N}}}$
in G with the property that, for any distinct
$(h^{(\ell )}_k)_{k\in {\mathbb {N}}}$
in G with the property that, for any distinct
![]() $i,j\in \{1,\ldots ,\ell \}$
,
$i,j\in \{1,\ldots ,\ell \}$
,
Hence, one can find non-degenerated sequences
![]() $(\textbf g_k^{(j)})_{k\in {\mathbb {N}}}$
in
$(\textbf g_k^{(j)})_{k\in {\mathbb {N}}}$
in
![]() $G^{\ell }$
,
$G^{\ell }$
,
![]() $j\in \{2,\ldots ,\ell \}$
, such that
$j\in \{2,\ldots ,\ell \}$
, such that
![]() $(\textbf g^{(1)}_k)_{k\in {\mathbb {N}}},\ldots,$
$(\textbf g^{(1)}_k)_{k\in {\mathbb {N}}},\ldots,$
![]() $(\textbf g^{(\ell )}_k)_{k\in {\mathbb {N}}}$
are essentially distinct. By (iii), there exists an
$(\textbf g^{(\ell )}_k)_{k\in {\mathbb {N}}}$
are essentially distinct. By (iii), there exists an
![]() $\alpha \in {\mathbb {N}}^{(\ell )}$
for which
$\alpha \in {\mathbb {N}}^{(\ell )}$
for which
 $$ \begin{align*}(g^{(1)}_{\alpha},\ldots,g^{(\ell)}_{\alpha})\in\mathcal R_{\epsilon}(A_0,A_1,\underbrace{X,\ldots,X}_{\ell-1\text{ times}}).\end{align*} $$
$$ \begin{align*}(g^{(1)}_{\alpha},\ldots,g^{(\ell)}_{\alpha})\in\mathcal R_{\epsilon}(A_0,A_1,\underbrace{X,\ldots,X}_{\ell-1\text{ times}}).\end{align*} $$
This implies that
![]() $g^{(1)}_{\alpha }\in R_{\epsilon }(A_0,A_1)$
.
$g^{(1)}_{\alpha }\in R_{\epsilon }(A_0,A_1)$
.
(iv)
![]() $\implies $
(i): We will show that, for any
$\implies $
(i): We will show that, for any
![]() $\xi ,\eta \in L_0^2(\mu )=\{f\in L^2(\mu )\,|\,\int _Xf\,\text {d}\mu =0\}$
,
$\xi ,\eta \in L_0^2(\mu )=\{f\in L^2(\mu )\,|\,\int _Xf\,\text {d}\mu =0\}$
,
![]() $\lim _{g\rightarrow \infty }\langle T_g\xi ,\eta \rangle =0$
. To do this, it suffices to prove that for any sequence
$\lim _{g\rightarrow \infty }\langle T_g\xi ,\eta \rangle =0$
. To do this, it suffices to prove that for any sequence
![]() $(g_k)_{k\in {\mathbb {N}}}$
in G with
$(g_k)_{k\in {\mathbb {N}}}$
in G with
![]() $\lim _{k\rightarrow \infty }g_k=\infty $
, there exists an increasing sequence
$\lim _{k\rightarrow \infty }g_k=\infty $
, there exists an increasing sequence
![]() $(k_j)_{j\in {\mathbb {N}}}$
in
$(k_j)_{j\in {\mathbb {N}}}$
in
![]() ${\mathbb {N}}$
such that, for any
${\mathbb {N}}$
such that, for any
![]() $\xi ,\eta \in L^2_0(\mu )$
,
$\xi ,\eta \in L^2_0(\mu )$
,
Let
![]() $(g_k)_{k\in {\mathbb {N}}}\subseteq G$
with
$(g_k)_{k\in {\mathbb {N}}}\subseteq G$
with
![]() $\lim _{k\rightarrow \infty }g_k=\infty $
. Let
$\lim _{k\rightarrow \infty }g_k=\infty $
. Let
![]() $(\textbf g_k)_{k\in {\mathbb {N}}}=(\underbrace {g_k,\ldots ,g_k}_{\ell \text { times}})_{k\in {\mathbb {N}}}$
(note that
$(\textbf g_k)_{k\in {\mathbb {N}}}=(\underbrace {g_k,\ldots ,g_k}_{\ell \text { times}})_{k\in {\mathbb {N}}}$
(note that
![]() $(\textbf g_k)_{k\in {\mathbb {N}}}$
is a non-degenerated sequence in
$(\textbf g_k)_{k\in {\mathbb {N}}}$
is a non-degenerated sequence in
![]() $G^{\ell }$
). We claim that there exist an increasing sequence
$G^{\ell }$
). We claim that there exist an increasing sequence
![]() $(k_j)_{j\in {\mathbb {N}}}$
in
$(k_j)_{j\in {\mathbb {N}}}$
in
![]() ${\mathbb {N}}$
and a bounded linear operator
${\mathbb {N}}$
and a bounded linear operator
![]() $V:L^2_0(\mu )\rightarrow L^2_0(\mu )$
such that, if we set
$V:L^2_0(\mu )\rightarrow L^2_0(\mu )$
such that, if we set
![]() $S=\{k_j\,|\,j\in {\mathbb {N}}\}$
, the following assertions hold.
$S=\{k_j\,|\,j\in {\mathbb {N}}\}$
, the following assertions hold.
-
(1) For any
 $\xi ,\eta \in L_0^2(\mu )$
, (3.3)
$\xi ,\eta \in L_0^2(\mu )$
, (3.3) $$ \begin{align} \langle V\xi,\eta\rangle =\lim_{j\rightarrow\infty}\langle T_{g_{k_j}}\xi,\eta\rangle. \end{align} $$
$$ \begin{align} \langle V\xi,\eta\rangle =\lim_{j\rightarrow\infty}\langle T_{g_{k_j}}\xi,\eta\rangle. \end{align} $$
-
(2) For any
 $A_0,A_1\in \mathcal A$
, there exists a real number
$A_0,A_1\in \mathcal A$
, there exists a real number
 $r_{A_0,A_1}$
such that (3.4)
$r_{A_0,A_1}$
such that (3.4) $$ \begin{align} {\mathop { \mathcal {R}{\text{-}\mathrm{lim}}}_{{\alpha\in S^{(\ell)}}}}\, \mu(A_0\cap T_{-g_{\alpha}}A_1)=r_{A_0,A_1}. \end{align} $$
$$ \begin{align} {\mathop { \mathcal {R}{\text{-}\mathrm{lim}}}_{{\alpha\in S^{(\ell)}}}}\, \mu(A_0\cap T_{-g_{\alpha}}A_1)=r_{A_0,A_1}. \end{align} $$
Let
![]() $\mathcal D$
be a countable dense subset of
$\mathcal D$
be a countable dense subset of
![]() $L_0^2(\mu )$
. By a diagonalization argument, one obtains an increasing sequence
$L_0^2(\mu )$
. By a diagonalization argument, one obtains an increasing sequence
![]() $(k^{\prime }_j)_{j\in {\mathbb {N}}}$
for which the limit in (3.3) exists for any
$(k^{\prime }_j)_{j\in {\mathbb {N}}}$
for which the limit in (3.3) exists for any
![]() $\xi ,\eta \in \mathcal D$
. Diagonalizing once more, we can pick a subsequence
$\xi ,\eta \in \mathcal D$
. Diagonalizing once more, we can pick a subsequence
![]() $(k_j)_{j\in {\mathbb {N}}}$
of
$(k_j)_{j\in {\mathbb {N}}}$
of
![]() $(k^{\prime }_j)_{j\in {\mathbb {N}}}$
for which (3.4) holds for any
$(k^{\prime }_j)_{j\in {\mathbb {N}}}$
for which (3.4) holds for any
![]() $A_0,A_1$
from a countable dense subset of
$A_0,A_1$
from a countable dense subset of
![]() $\mathcal A$
. It follows (by a standard approximation argument) that all the limits appearing in (3.3) and (3.4) exist for any
$\mathcal A$
. It follows (by a standard approximation argument) that all the limits appearing in (3.3) and (3.4) exist for any
![]() $\xi ,\eta \in L_0^2(\mu )$
and any
$\xi ,\eta \in L_0^2(\mu )$
and any
![]() $A_0,A_1\in \mathcal A$
. Notice that (3.3) holds for a unique linear operator V. Since
$A_0,A_1\in \mathcal A$
. Notice that (3.3) holds for a unique linear operator V. Since
we have that V is norm-bounded.
We claim that
![]() $V^{\ell }=0$
. To see this, note that, by (iv), for every
$V^{\ell }=0$
. To see this, note that, by (iv), for every
![]() $A_0,A_1\in \mathcal A$
,
$A_0,A_1\in \mathcal A$
,
![]() $r_{A_0,A_1}=\mu (A_0)\mu (A_1)$
(otherwise we would be able to find an
$r_{A_0,A_1}=\mu (A_0)\mu (A_1)$
(otherwise we would be able to find an
![]() $\epsilon>0$
for which the set
$\epsilon>0$
for which the set
![]() $\mathcal R_{\epsilon }(A_0,A_1)$
is not
$\mathcal R_{\epsilon }(A_0,A_1)$
is not
![]() $\Sigma _{\ell }^*$
). Since the linear combinations of indicator functions are dense in
$\Sigma _{\ell }^*$
). Since the linear combinations of indicator functions are dense in
![]() $L^2(\mu )$
, it follows that, for any
$L^2(\mu )$
, it follows that, for any
![]() $f_1,f_2\in L^2(\mu )$
,
$f_1,f_2\in L^2(\mu )$
,
Observe that, by (3.3),
![]() $T_gV=VT_g$
for all
$T_gV=VT_g$
for all
![]() $g\in G$
. Thus, all the limits appearing in the expression
$g\in G$
. Thus, all the limits appearing in the expression
exist for any
![]() $\xi ,\eta \in L_0^2(\mu )$
. Combining (3.3) and (3.5), we obtain that, for any
$\xi ,\eta \in L_0^2(\mu )$
. Combining (3.3) and (3.5), we obtain that, for any
![]() $\xi ,\eta \in L_0^2(\mu )$
,
$\xi ,\eta \in L_0^2(\mu )$
,
 $$ \begin{align*}0&= {\mathop { \mathcal {R}{\text{-}\mathrm{lim}}}_{{\alpha\in S^{(\ell)}}}} \int_X \overline \eta T_{g_{\alpha}}\xi\,\text{d}\mu={\mathop { \mathcal {R}{\text{-}\mathrm{lim}}}_{{\alpha\in S^{(\ell)}}}} \langle T_{g_{\alpha}}\xi,\eta\rangle\\ &=\lim_{j_1\rightarrow\infty}\cdots\lim_{j_{\ell}\rightarrow\infty}\langle T_{(g_{k_{j_1}}+\cdots+g_{k_{j_{\ell}}})}\xi,\eta\rangle=\langle V^{\ell}\xi,\eta\rangle,\end{align*} $$
$$ \begin{align*}0&= {\mathop { \mathcal {R}{\text{-}\mathrm{lim}}}_{{\alpha\in S^{(\ell)}}}} \int_X \overline \eta T_{g_{\alpha}}\xi\,\text{d}\mu={\mathop { \mathcal {R}{\text{-}\mathrm{lim}}}_{{\alpha\in S^{(\ell)}}}} \langle T_{g_{\alpha}}\xi,\eta\rangle\\ &=\lim_{j_1\rightarrow\infty}\cdots\lim_{j_{\ell}\rightarrow\infty}\langle T_{(g_{k_{j_1}}+\cdots+g_{k_{j_{\ell}}})}\xi,\eta\rangle=\langle V^{\ell}\xi,\eta\rangle,\end{align*} $$
proving our claim.
It follows that in order to prove that (3.2) holds, it is enough to show that
![]() $L_0^2(\mu )=\text {Ker}(V^{\ell })\subseteq \text {Ker}(V)$
. To do this, we will first show that V is a normal operator. Indeed, for any
$L_0^2(\mu )=\text {Ker}(V^{\ell })\subseteq \text {Ker}(V)$
. To do this, we will first show that V is a normal operator. Indeed, for any
![]() $\xi ,\eta \in L^2_0(\mu )$
,
$\xi ,\eta \in L^2_0(\mu )$
,
and, hence,
So, for any
![]() $\xi \in L_0^2(\mu )$
,
$\xi \in L_0^2(\mu )$
,
Now take
![]() $t\in {\mathbb {N}}$
,
$t\in {\mathbb {N}}$
,
![]() $\eta \in L^2_0(\mu )$
, and set
$\eta \in L^2_0(\mu )$
, and set
![]() $\xi =V^{t-1}\eta $
. Suppose that
$\xi =V^{t-1}\eta $
. Suppose that
![]() $\eta \not \in \text {Ker}(V^t)$
. Then
$\eta \not \in \text {Ker}(V^t)$
. Then
![]() $\xi \not \in \text {Ker}(V)$
and, by (3.6),
$\xi \not \in \text {Ker}(V)$
and, by (3.6),
![]() $\langle V^*V\xi ,\xi \rangle \neq 0$
. Applying (3.6) to
$\langle V^*V\xi ,\xi \rangle \neq 0$
. Applying (3.6) to
![]() $V\xi $
, we obtain
$V\xi $
, we obtain
![]() $\|V^2\xi \|^2=\|V^*V\xi \|^2$
. So, since
$\|V^2\xi \|^2=\|V^*V\xi \|^2$
. So, since
![]() $\langle V^*V\xi ,\xi \rangle \neq 0$
,
$\langle V^*V\xi ,\xi \rangle \neq 0$
,
![]() $V^{t+1}\eta =V^2\xi \neq 0$
. This proves that, for each
$V^{t+1}\eta =V^2\xi \neq 0$
. This proves that, for each
![]() $t\in {\mathbb {N}}$
, if
$t\in {\mathbb {N}}$
, if
![]() $\eta \not \in \text {Ker}(V^t)$
, then
$\eta \not \in \text {Ker}(V^t)$
, then
![]() $\eta \not \in \text {Ker}(V^{t+1})$
. So,
$\eta \not \in \text {Ker}(V^{t+1})$
. So,
![]() $L_0^2(\mu )=\text {Ker}(V^{\ell })\subseteq \text {Ker}(V)$
and, hence, for any
$L_0^2(\mu )=\text {Ker}(V^{\ell })\subseteq \text {Ker}(V)$
and, hence, for any
![]() $\xi ,\eta \in L^2_0(\mu )$
,
$\xi ,\eta \in L^2_0(\mu )$
,
4 Some ‘diagonal’ results for strongly mixing systems
In order to give the reader the flavor of the main theme of this section, we start by formulating a slightly enhanced form of Theorem 1.4. (This theorem is a rather special case of the results of ‘diagonal’ nature to be proved in this section.)
Proposition 4.1. Let
![]() $(X,\mathcal A,\mu , T)$
be a measure-preserving system and let
$(X,\mathcal A,\mu , T)$
be a measure-preserving system and let
![]() $a_1,\ldots ,a_{\ell }$
be non-zero distinct integers. Then T is strongly mixing if and only if, for any
$a_1,\ldots ,a_{\ell }$
be non-zero distinct integers. Then T is strongly mixing if and only if, for any
![]() $A_0,\ldots ,A_{\ell }\in \mathcal A$
and any
$A_0,\ldots ,A_{\ell }\in \mathcal A$
and any
![]() $\epsilon>0$
, the set
$\epsilon>0$
, the set
 $$ \begin{align*}\bigg\{n\in{\mathbb{Z}}\,\bigg|\,\,\bigg|\mu(A_0\cap T^{a_1n}A_1\cap\cdots\cap T^{a_{\ell} n}A_{\ell})-\prod_{j=0}^{\ell}\mu(A_j)\bigg|<\epsilon\bigg\}\end{align*} $$
$$ \begin{align*}\bigg\{n\in{\mathbb{Z}}\,\bigg|\,\,\bigg|\mu(A_0\cap T^{a_1n}A_1\cap\cdots\cap T^{a_{\ell} n}A_{\ell})-\prod_{j=0}^{\ell}\mu(A_j)\bigg|<\epsilon\bigg\}\end{align*} $$
is
![]() $\Sigma _{\ell }^*$
.
$\Sigma _{\ell }^*$
.
We move now to formulations of more general ‘diagonal’ results.
Let
![]() $(G,{\kern-1pt}+)$
be a countable abelian group, let
$(G,{\kern-1pt}+)$
be a countable abelian group, let
![]() $(X,{\kern-1pt}\mathcal A,{\kern-1pt}\mu ,{\kern-1pt} (T_g)_{g\in G})$
be a measure-preserving system, let
$(X,{\kern-1pt}\mathcal A,{\kern-1pt}\mu ,{\kern-1pt} (T_g)_{g\in G})$
be a measure-preserving system, let
![]() $\ell \in {\mathbb {N}}$
and let
$\ell \in {\mathbb {N}}$
and let
![]() $\phi _1,\ldots ,\phi _{\ell }:G\rightarrow G$
be homomorphisms. For any
$\phi _1,\ldots ,\phi _{\ell }:G\rightarrow G$
be homomorphisms. For any
![]() $\epsilon>0$
and any
$\epsilon>0$
and any
![]() $A_0,\ldots ,A_{\ell }\in \mathcal A$
, define
$A_0,\ldots ,A_{\ell }\in \mathcal A$
, define
 $$ \begin{align*}R_{\epsilon}^{\phi_1,\ldots,\phi_{\ell}}(A_0,\ldots,A_{\ell}){\kern-1pt}={\kern-1pt}\bigg\{{\kern-1pt}g{\kern-1pt}\in{\kern-1pt} G\,\bigg|\,\bigg|\mu(A_0\cap T_{\phi_1(g)}A_1{\kern-1pt}\cap\cdots\cap{\kern-1pt} T_{\phi_{\ell}(g)}A_{\ell}){\kern-1pt}-\!\prod_{j=0}^{\ell}{\kern-1pt}\mu(A_j)\bigg|\!<{\kern-1pt}\epsilon{\kern-1pt}\bigg\}.\end{align*} $$
$$ \begin{align*}R_{\epsilon}^{\phi_1,\ldots,\phi_{\ell}}(A_0,\ldots,A_{\ell}){\kern-1pt}={\kern-1pt}\bigg\{{\kern-1pt}g{\kern-1pt}\in{\kern-1pt} G\,\bigg|\,\bigg|\mu(A_0\cap T_{\phi_1(g)}A_1{\kern-1pt}\cap\cdots\cap{\kern-1pt} T_{\phi_{\ell}(g)}A_{\ell}){\kern-1pt}-\!\prod_{j=0}^{\ell}{\kern-1pt}\mu(A_j)\bigg|\!<{\kern-1pt}\epsilon{\kern-1pt}\bigg\}.\end{align*} $$
We first give two equivalent formulations of a general result which deals with finitely generated groups.
Theorem 4.2. Let
![]() $(G,+)$
be a finitely generated abelian group, let
$(G,+)$
be a finitely generated abelian group, let
![]() $(X,\mathcal A,\mu , (T_g)_{g\in G})$
be a measure-preserving system and let the homomorphisms
$(X,\mathcal A,\mu , (T_g)_{g\in G})$
be a measure-preserving system and let the homomorphisms
![]() $\phi _1,\ldots ,\phi _{\ell }:G\rightarrow G$
be such that, for any
$\phi _1,\ldots ,\phi _{\ell }:G\rightarrow G$
be such that, for any
![]() $j\in \{1,\ldots ,\ell \}$
,
$j\in \{1,\ldots ,\ell \}$
,
![]() $\ker (\phi _j)$
is finite and, for any
$\ker (\phi _j)$
is finite and, for any
![]() $i\neq j$
,
$i\neq j$
,
![]() $\ker (\phi _j-\phi _i)$
is also finite. Then
$\ker (\phi _j-\phi _i)$
is also finite. Then
![]() $(T_g)_{g\in G}$
is strongly mixing if and only if, for any
$(T_g)_{g\in G}$
is strongly mixing if and only if, for any
![]() $A_0,\ldots ,A_{\ell }\in \mathcal A$
and any
$A_0,\ldots ,A_{\ell }\in \mathcal A$
and any
![]() $\epsilon>0$
, the set
$\epsilon>0$
, the set
![]() $R_{\epsilon }^{\phi _1,\ldots ,\phi _{\ell }}(A_0,\ldots ,A_{\ell })$
is
$R_{\epsilon }^{\phi _1,\ldots ,\phi _{\ell }}(A_0,\ldots ,A_{\ell })$
is
![]() $\Sigma _{\ell }^*$
.
$\Sigma _{\ell }^*$
.
Note that if G is a finitely generated abelian group and
![]() $\phi :G\rightarrow G$
is a homomorphism,
$\phi :G\rightarrow G$
is a homomorphism,
![]() $\ker (\phi )$
is finite if and only if the index of
$\ker (\phi )$
is finite if and only if the index of
![]() $\phi (G)$
in G is finite. It follows that Theorem 4.2 can be formulated in the following equivalent form.
$\phi (G)$
in G is finite. It follows that Theorem 4.2 can be formulated in the following equivalent form.
Theorem 4.3. Let
![]() $(G,+)$
be a finitely generated abelian group, let
$(G,+)$
be a finitely generated abelian group, let
![]() $(X,\mathcal A,\mu , (T_g)_{g\in G})$
be a measure-preserving system and let the homomorphisms
$(X,\mathcal A,\mu , (T_g)_{g\in G})$
be a measure-preserving system and let the homomorphisms
![]() $\phi _1,\ldots ,\phi _{\ell }:G\rightarrow G$
be such that, for any
$\phi _1,\ldots ,\phi _{\ell }:G\rightarrow G$
be such that, for any
![]() $j\in \{1,\ldots ,\ell \}$
, the index of
$j\in \{1,\ldots ,\ell \}$
, the index of
![]() $\phi _j(G)$
in G is finite and, for any
$\phi _j(G)$
in G is finite and, for any
![]() $i\neq j$
, the index of
$i\neq j$
, the index of
![]() $(\phi _j-\phi _i)$
in G is also finite. Then
$(\phi _j-\phi _i)$
in G is also finite. Then
![]() $(T_g)_{g\in G}$
is strongly mixing if and only if, for any
$(T_g)_{g\in G}$
is strongly mixing if and only if, for any
![]() $A_0,\ldots ,A_{\ell }\in \mathcal A$
and any
$A_0,\ldots ,A_{\ell }\in \mathcal A$
and any
![]() $\epsilon>0$
, the set
$\epsilon>0$
, the set
![]() $R_{\epsilon }^{\phi _1,\ldots ,\phi _{\ell }}(A_0,\ldots ,A_{\ell })$
is
$R_{\epsilon }^{\phi _1,\ldots ,\phi _{\ell }}(A_0,\ldots ,A_{\ell })$
is
![]() $\Sigma _{\ell }^*$
.
$\Sigma _{\ell }^*$
.
We now formulate and prove variants of Theorems 4.2 and 4.3 which pertain to mixing actions of general (not necessarily finitely generated) countable abelian groups. Unlike Theorems 4.2 and 4.3, the following two theorems are not equivalent. We will provide the relevant counterexamples at the end of this section.
Theorem 4.4. Let
![]() $(G,+)$
be a countable abelian group, let
$(G,+)$
be a countable abelian group, let
![]() $(X,\mathcal A,\mu ,(T_g)_{g\in G})$
be a strongly mixing system and let the homomorphisms
$(X,\mathcal A,\mu ,(T_g)_{g\in G})$
be a strongly mixing system and let the homomorphisms
![]() $\phi _1,\ldots ,\phi _{\ell }:G\rightarrow G$
be such that, for any
$\phi _1,\ldots ,\phi _{\ell }:G\rightarrow G$
be such that, for any
![]() $j\in \{1,\ldots ,\ell \}$
,
$j\in \{1,\ldots ,\ell \}$
,
![]() $\ker (\phi _j)$
is finite and, for any
$\ker (\phi _j)$
is finite and, for any
![]() $i\neq j$
,
$i\neq j$
,
![]() $\ker (\phi _j-\phi _i)$
is also finite. For any non-degenerated sequence
$\ker (\phi _j-\phi _i)$
is also finite. For any non-degenerated sequence
![]() $(\textbf g_k)_{k\in {\mathbb {N}}}=(g_{k,1},\ldots ,g_{k,\ell })_{k\in {\mathbb {N}}}$
in
$(\textbf g_k)_{k\in {\mathbb {N}}}=(g_{k,1},\ldots ,g_{k,\ell })_{k\in {\mathbb {N}}}$
in
![]() $G^{\ell }$
, there exists an infinite set
$G^{\ell }$
, there exists an infinite set
![]() $S\subseteq {\mathbb {N}}$
such that, for any
$S\subseteq {\mathbb {N}}$
such that, for any
![]() $A_0,\ldots ,A_{\ell } \in \mathcal A$
,
$A_0,\ldots ,A_{\ell } \in \mathcal A$
,
 $$ \begin{align*}{\mathop { \mathcal {R}{\text{-}\mathrm{lim}}}_{{\alpha\in S^{(\ell)}}}}\, \mu(A_0\cap T_{\phi_1(g_{\alpha})}A_1\cap\cdots\cap T_{\phi_{\ell}(g_{\alpha})}A_{\ell})=\prod_{j=0}^{\ell} \mu(A_j).\end{align*} $$
$$ \begin{align*}{\mathop { \mathcal {R}{\text{-}\mathrm{lim}}}_{{\alpha\in S^{(\ell)}}}}\, \mu(A_0\cap T_{\phi_1(g_{\alpha})}A_1\cap\cdots\cap T_{\phi_{\ell}(g_{\alpha})}A_{\ell})=\prod_{j=0}^{\ell} \mu(A_j).\end{align*} $$
Equivalently, for any
![]() $A_0,\ldots ,A_{\ell } \in \mathcal A$
and any
$A_0,\ldots ,A_{\ell } \in \mathcal A$
and any
![]() $\epsilon>0$
, the set
$\epsilon>0$
, the set
![]() $R_{\epsilon }^{\phi _1,\ldots ,\phi _{\ell }}(A_0,\ldots ,A_{\ell })$
is
$R_{\epsilon }^{\phi _1,\ldots ,\phi _{\ell }}(A_0,\ldots ,A_{\ell })$
is
![]() $\Sigma _{\ell }^*$
.
$\Sigma _{\ell }^*$
.
Proof. Since, for any distinct
![]() $i,j\in \{1,\ldots ,\ell \}$
,
$i,j\in \{1,\ldots ,\ell \}$
,
![]() $\ker (\phi _j)$
and
$\ker (\phi _j)$
and
![]() $\ker (\phi _j-\phi _i)$
are both finite, we have for each
$\ker (\phi _j-\phi _i)$
are both finite, we have for each
![]() $t\in \{1,\ldots ,\ell \}$
,
$t\in \{1,\ldots ,\ell \}$
,
For each
![]() $j\in \{1,\ldots ,\ell \}$
, let
$j\in \{1,\ldots ,\ell \}$
, let
Then the sequences
![]() $(\textbf g^{(1)}_k)_{k\in {\mathbb {N}}},\ldots ,(\textbf g^{(\ell )}_k)_{k\in {\mathbb {N}}}$
are non-degenerated and essentially distinct. By Theorem 3.1(ii), there exists an infinite set
$(\textbf g^{(1)}_k)_{k\in {\mathbb {N}}},\ldots ,(\textbf g^{(\ell )}_k)_{k\in {\mathbb {N}}}$
are non-degenerated and essentially distinct. By Theorem 3.1(ii), there exists an infinite set
![]() $S\subseteq {\mathbb {N}}$
such that, for any
$S\subseteq {\mathbb {N}}$
such that, for any
![]() $A_0,\ldots ,A_{\ell }\in \mathcal A$
,
$A_0,\ldots ,A_{\ell }\in \mathcal A$
,
 $$ \begin{align*} &{\mathop { \mathcal {R}{\text{-}\mathrm{lim}}}_{{\alpha\in S^{(\ell)}}}}\, \mu(A_0\cap T_{\phi_1(g_{\alpha})}A_1\cap\cdots\cap T_{\phi_{\ell}(g_{\alpha})}A_{\ell})\\ &\quad={\mathop { \mathcal {R}{\text{-}\mathrm{lim}}}_{{\alpha\in S^{(\ell)}}}}\, \mu(A_0\cap T_{g^{(1)}_{\alpha}}A_1\cap\cdots\cap T_{g^{(\ell)}_{\alpha}}A_{\ell})=\mu\bigg(\prod_{j=0}^{\ell} A_j\bigg).\\[-3.8pc] \end{align*} $$
$$ \begin{align*} &{\mathop { \mathcal {R}{\text{-}\mathrm{lim}}}_{{\alpha\in S^{(\ell)}}}}\, \mu(A_0\cap T_{\phi_1(g_{\alpha})}A_1\cap\cdots\cap T_{\phi_{\ell}(g_{\alpha})}A_{\ell})\\ &\quad={\mathop { \mathcal {R}{\text{-}\mathrm{lim}}}_{{\alpha\in S^{(\ell)}}}}\, \mu(A_0\cap T_{g^{(1)}_{\alpha}}A_1\cap\cdots\cap T_{g^{(\ell)}_{\alpha}}A_{\ell})=\mu\bigg(\prod_{j=0}^{\ell} A_j\bigg).\\[-3.8pc] \end{align*} $$
Remark 4.5. The goal of this remark is to indicate an alternative way of proving Theorem 4.4. Let G and
![]() $\phi _1,\ldots ,\phi _{\ell }$
be as in the hypothesis of Theorem 4.4. In §5 we will show that if E is a
$\phi _1,\ldots ,\phi _{\ell }$
be as in the hypothesis of Theorem 4.4. In §5 we will show that if E is a
![]() $\tilde {\Sigma }_{\ell }^*$
set in
$\tilde {\Sigma }_{\ell }^*$
set in
![]() $G^{\ell }$
, then
$G^{\ell }$
, then
![]() $\{g\in G\,|\,(\phi _1(g),\ldots ,\phi _{\ell }(g))\in E\}$
is a
$\{g\in G\,|\,(\phi _1(g),\ldots ,\phi _{\ell }(g))\in E\}$
is a
![]() $\Sigma _{\ell }^*$
set in G (see Proposition 5.22). Thus, for any measure-preserving system
$\Sigma _{\ell }^*$
set in G (see Proposition 5.22). Thus, for any measure-preserving system
![]() $(X,\mathcal A,\mu , (T_g)_{g\in G})$
, any
$(X,\mathcal A,\mu , (T_g)_{g\in G})$
, any
![]() $A_0,\ldots ,A_{\ell }\in \mathcal A$
and any
$A_0,\ldots ,A_{\ell }\in \mathcal A$
and any
![]() $\epsilon>0$
, if
$\epsilon>0$
, if
![]() $R_{\epsilon }(A_0,\ldots ,A_{\ell })$
is a
$R_{\epsilon }(A_0,\ldots ,A_{\ell })$
is a
![]() $\tilde {\Sigma }_{\ell }^*$
set, then
$\tilde {\Sigma }_{\ell }^*$
set, then
![]() $R_{\epsilon }^{\phi _1,\ldots ,\phi _{\ell }}(A_0,\ldots ,A_{\ell })$
is a
$R_{\epsilon }^{\phi _1,\ldots ,\phi _{\ell }}(A_0,\ldots ,A_{\ell })$
is a
![]() $\Sigma _{\ell }^*$
set. One can now invoke Theorem 3.1(iii).
$\Sigma _{\ell }^*$
set. One can now invoke Theorem 3.1(iii).
The next result complements Theorem 4.4. Note that it provides a somewhat stronger version of one of the directions in Theorem 4.3.
Theorem 4.6. Let
![]() $(G,+)$
be a countable abelian group, let
$(G,+)$
be a countable abelian group, let
![]() $(X,\mathcal A,\mu ,(T_g)_{g\in G})$
be a measure-preserving system and let the homomorphisms
$(X,\mathcal A,\mu ,(T_g)_{g\in G})$
be a measure-preserving system and let the homomorphisms
![]() $\phi _1,\ldots ,\phi _{\ell }:G\rightarrow G$
be such that at least one of
$\phi _1,\ldots ,\phi _{\ell }:G\rightarrow G$
be such that at least one of
![]() $\phi _1(G)$
,
$\phi _1(G)$
,
![]() $\phi _2(G)$
,
$\phi _2(G)$
,
![]() $(\phi _2-\phi _1)(G)$
has finite index in G. If, for all
$(\phi _2-\phi _1)(G)$
has finite index in G. If, for all
![]() $A_0,\ldots ,A_{\ell }\in \mathcal A$
and all
$A_0,\ldots ,A_{\ell }\in \mathcal A$
and all
![]() $\epsilon>0$
, the set
$\epsilon>0$
, the set
![]() $R_{\epsilon }^{\phi _1,\ldots ,\phi _{\ell }}(A_0,\ldots ,A_{\ell })$
is
$R_{\epsilon }^{\phi _1,\ldots ,\phi _{\ell }}(A_0,\ldots ,A_{\ell })$
is
![]() $\Sigma _{\ell }^*$
, then
$\Sigma _{\ell }^*$
, then
![]() $(T_g)_{g\in G}$
is strongly mixing.
$(T_g)_{g\in G}$
is strongly mixing.
Proof. We will assume that
![]() $(\phi _2-\phi _1)(G)$
has finite index in G; the other two cases can be handled similarly. For any
$(\phi _2-\phi _1)(G)$
has finite index in G; the other two cases can be handled similarly. For any
![]() $A_1,A_2\in \mathcal A$
and any
$A_1,A_2\in \mathcal A$
and any
![]() $\epsilon>0$
, we have
$\epsilon>0$
, we have
 $$ \begin{align*} &R^{\phi_1,\ldots,\phi_{\ell}}_{\epsilon}(X,A_1,A_2,\underbrace{X,\ldots,X}_{\ell-2\text{ times}})\\ &\quad=\{g\in G\,|\,|\mu(X\cap T_{\phi_1(g)}A_1\cap T_{\phi_2(g)}A_2\cap T_{\phi_3(g)} X\cap\cdots\cap T_{\phi_{\ell}(g)}X)\\ &\qquad-\mu(A_1)\mu(A_2)|<\epsilon\}\\ &\quad=\{g\in G\,|\,|\mu(T_{\phi_1(g)}A_1\cap T_{\phi_2(g)}A_2)-\mu(A_1)\mu(A_2)|<\epsilon\}=R_{\epsilon}^{\phi_2-\phi_1}(A_1,A_2). \end{align*} $$
$$ \begin{align*} &R^{\phi_1,\ldots,\phi_{\ell}}_{\epsilon}(X,A_1,A_2,\underbrace{X,\ldots,X}_{\ell-2\text{ times}})\\ &\quad=\{g\in G\,|\,|\mu(X\cap T_{\phi_1(g)}A_1\cap T_{\phi_2(g)}A_2\cap T_{\phi_3(g)} X\cap\cdots\cap T_{\phi_{\ell}(g)}X)\\ &\qquad-\mu(A_1)\mu(A_2)|<\epsilon\}\\ &\quad=\{g\in G\,|\,|\mu(T_{\phi_1(g)}A_1\cap T_{\phi_2(g)}A_2)-\mu(A_1)\mu(A_2)|<\epsilon\}=R_{\epsilon}^{\phi_2-\phi_1}(A_1,A_2). \end{align*} $$
By our assumption, for any
![]() $\epsilon>0$
and any
$\epsilon>0$
and any
![]() $A_1,A_2\in \mathcal A$
, the set
$A_1,A_2\in \mathcal A$
, the set
![]() $R^{\phi _2-\phi _1}_{\epsilon }(A_1,A_2)$
is a
$R^{\phi _2-\phi _1}_{\epsilon }(A_1,A_2)$
is a
![]() $\Sigma _{\ell }^*$
set and hence, by Theorem 3.1(iv),
$\Sigma _{\ell }^*$
set and hence, by Theorem 3.1(iv),
![]() $(T_{(\phi _2-\phi _1)(g)})_{g\in G}$
is strongly mixing.
$(T_{(\phi _2-\phi _1)(g)})_{g\in G}$
is strongly mixing.
We will now prove that
![]() $(T_g)_{g\in G}$
is strongly mixing by showing that for any sequence
$(T_g)_{g\in G}$
is strongly mixing by showing that for any sequence
![]() $(g_k)_{k\in {\mathbb {N}}}$
in G with
$(g_k)_{k\in {\mathbb {N}}}$
in G with
![]() $\lim _{k\rightarrow \infty }g_k=\infty $
, there exists an increasing sequence
$\lim _{k\rightarrow \infty }g_k=\infty $
, there exists an increasing sequence
![]() $(k_j)_{j\in {\mathbb {N}}}$
in
$(k_j)_{j\in {\mathbb {N}}}$
in
![]() ${\mathbb {N}}$
with the property that for any
${\mathbb {N}}$
with the property that for any
![]() $A_0,A_1\in \mathcal A$
,
$A_0,A_1\in \mathcal A$
,
Let
![]() $(g_k)_{k\in {\mathbb {N}}}$
be a sequence in G with
$(g_k)_{k\in {\mathbb {N}}}$
be a sequence in G with
![]() $\lim _{k\rightarrow \infty }g_k=\infty $
. By assumption,
$\lim _{k\rightarrow \infty }g_k=\infty $
. By assumption,
![]() $(\phi _2-\phi _1)(G)$
has finite index in G, so there exist an increasing sequence
$(\phi _2-\phi _1)(G)$
has finite index in G, so there exist an increasing sequence
![]() $(k_j)_{j\in {\mathbb {N}}}$
in
$(k_j)_{j\in {\mathbb {N}}}$
in
![]() ${\mathbb {N}}$
and an element
${\mathbb {N}}$
and an element
![]() $\tau \in G$
for which
$\tau \in G$
for which
![]() $\{g_{k_j}+\tau \,|\,j\in {\mathbb {N}}\}\subseteq (\phi _2-\phi _1)(G)$
. Since
$\{g_{k_j}+\tau \,|\,j\in {\mathbb {N}}\}\subseteq (\phi _2-\phi _1)(G)$
. Since
![]() $(T_{(\phi _2-\phi _1)(g)})_{g\in G}$
is strongly mixing, for any
$(T_{(\phi _2-\phi _1)(g)})_{g\in G}$
is strongly mixing, for any
![]() $A_0,A_1\in \mathcal A$
,
$A_0,A_1\in \mathcal A$
,
completing the proof.
The following proposition shows that the assumption made in Theorem 4.2 that G is finitely generated cannot be removed.
Proposition 4.7. Let
![]() $G=\bigoplus _{k\in {\mathbb {N}}} {\mathbb {Z}}$
and let
$G=\bigoplus _{k\in {\mathbb {N}}} {\mathbb {Z}}$
and let
![]() $\ell \in {\mathbb {N}}$
. There exist a measure-preserving system
$\ell \in {\mathbb {N}}$
. There exist a measure-preserving system
![]() $(X,\mathcal A,\mu ,(T_g)_{g\in G})$
and homomorphisms
$(X,\mathcal A,\mu ,(T_g)_{g\in G})$
and homomorphisms
![]() $\phi _1,\ldots ,\phi _{\ell }:G\rightarrow G$
satisfying (a) for any
$\phi _1,\ldots ,\phi _{\ell }:G\rightarrow G$
satisfying (a) for any
![]() $j\in \{1,\ldots ,\ell \}$
,
$j\in \{1,\ldots ,\ell \}$
,
![]() $\ker (\phi _j)$
is finite, and (b) for any
$\ker (\phi _j)$
is finite, and (b) for any
![]() $i\neq j$
,
$i\neq j$
,
![]() $\ker (\phi _j-\phi _i)$
is also finite, and such that every set of the form
$\ker (\phi _j-\phi _i)$
is also finite, and such that every set of the form
![]() $R_{\epsilon }^{\phi _1,\ldots ,\phi _{\ell }} (A_0,\ldots ,A_{\ell })$
is
$R_{\epsilon }^{\phi _1,\ldots ,\phi _{\ell }} (A_0,\ldots ,A_{\ell })$
is
![]() $\Sigma _{\ell }^*$
but
$\Sigma _{\ell }^*$
but
![]() $(T_g)_{g\in G}$
is not strongly mixing.
$(T_g)_{g\in G}$
is not strongly mixing.
Proof. We will only carry out the proof for
![]() $\ell =2$
; the general case can be handled similarly. Let
$\ell =2$
; the general case can be handled similarly. Let
![]() $\phi _1:G\rightarrow G$
be the homomorphism given by
$\phi _1:G\rightarrow G$
be the homomorphism given by
Note that
![]() $\phi _1$
is injective (and so
$\phi _1$
is injective (and so
![]() $\ker (\phi _1)$
is trivial).
$\ker (\phi _1)$
is trivial).
Let
![]() $X=\{0,1\}^G$
be endowed with the product topology, let
$X=\{0,1\}^G$
be endowed with the product topology, let
![]() $\mu $
be the
$\mu $
be the
![]() $(\tfrac 12,\tfrac 12)$
product measure on
$(\tfrac 12,\tfrac 12)$
product measure on
![]() $\mathcal A=\text {Borel}(X)$
and, for each
$\mathcal A=\text {Borel}(X)$
and, for each
![]() $g\in G$
, let
$g\in G$
, let
![]() $S_g:X\rightarrow X$
be the map defined by
$S_g:X\rightarrow X$
be the map defined by
![]() $(S_g(x))(h)=x(h+g)$
. The system
$(S_g(x))(h)=x(h+g)$
. The system
![]() $(X,\mathcal A,\mu ,(S_g)_{g\in G})$
is strongly mixing. Define a measure-preserving G-action
$(X,\mathcal A,\mu ,(S_g)_{g\in G})$
is strongly mixing. Define a measure-preserving G-action
![]() $(T_g)_{g\in G}$
on
$(T_g)_{g\in G}$
on
![]() $(X,\mathcal A,\mu )$
by
$(X,\mathcal A,\mu )$
by
and let
![]() $\phi _2:G{\kern-1pt}\rightarrow{\kern-1pt} G$
be defined by
$\phi _2:G{\kern-1pt}\rightarrow{\kern-1pt} G$
be defined by
![]() $\phi _2(g){\kern-1pt}={\kern-1pt}2\phi _1(g)$
. Note that, for any
$\phi _2(g){\kern-1pt}={\kern-1pt}2\phi _1(g)$
. Note that, for any
![]() $g{\kern-1pt}={\kern-1pt}(a_1,a_2,\ldots ){\kern-1pt}\in{\kern-1pt} G$
,
$g{\kern-1pt}={\kern-1pt}(a_1,a_2,\ldots ){\kern-1pt}\in{\kern-1pt} G$
,
So, for any
![]() $\epsilon>0$
and any
$\epsilon>0$
and any
![]() $A_0,A_1,A_2\in \mathcal A$
,
$A_0,A_1,A_2\in \mathcal A$
,
 $$ \begin{align} &R_{\epsilon}^{\phi_1,\phi_2}(A_0,A_1,A_2)\nonumber\\ &\quad=\{g\in G\,|\,|\mu(A_0\cap T_{\phi_1(g)}A_1\cap T_{\phi_2(g)}A_2)-\mu(A_0)\mu(A_1)\mu(A_2)|<\epsilon\}\nonumber\\ &\quad=\{g\in G\,|\,|\mu(A_0\cap S_{g}A_1\cap S_{2g}A_2)-\mu(A_0)\mu(A_1)\mu(A_2)|<\epsilon\}. \end{align} $$
$$ \begin{align} &R_{\epsilon}^{\phi_1,\phi_2}(A_0,A_1,A_2)\nonumber\\ &\quad=\{g\in G\,|\,|\mu(A_0\cap T_{\phi_1(g)}A_1\cap T_{\phi_2(g)}A_2)-\mu(A_0)\mu(A_1)\mu(A_2)|<\epsilon\}\nonumber\\ &\quad=\{g\in G\,|\,|\mu(A_0\cap S_{g}A_1\cap S_{2g}A_2)-\mu(A_0)\mu(A_1)\mu(A_2)|<\epsilon\}. \end{align} $$
It follows from Theorem 4.4 that every set of the form
is
![]() $\Sigma _2^*$
and hence, by (4.1), for any
$\Sigma _2^*$
and hence, by (4.1), for any
![]() $A_0,A_1,A_2$
and any
$A_0,A_1,A_2$
and any
![]() $\epsilon>0$
,
$\epsilon>0$
,
![]() $R_{\epsilon }^{\phi _1,\phi _2}(A_0,A_1,A_2)$
is
$R_{\epsilon }^{\phi _1,\phi _2}(A_0,A_1,A_2)$
is
![]() $\Sigma _2^*$
.
$\Sigma _2^*$
.
Noting that for each
![]() $k\in {\mathbb {N}}$
,
$k\in {\mathbb {N}}$
,
![]() $T_{(k,0,0,\ldots )}=S_{(0,0,\ldots )}$
is the identity map on X, we see that
$T_{(k,0,0,\ldots )}=S_{(0,0,\ldots )}$
is the identity map on X, we see that
![]() $(T_g)_{g\in G}$
is not strongly mixing. We are done.
$(T_g)_{g\in G}$
is not strongly mixing. We are done.
The next result shows that Theorem 4.3 cannot be extended to arbitrary countable abelian groups.
Proposition 4.8. Let
![]() $G=\bigoplus _{k\in {\mathbb {N}}} {\mathbb {Z}}$
and let
$G=\bigoplus _{k\in {\mathbb {N}}} {\mathbb {Z}}$
and let
![]() $\ell \in {\mathbb {N}}$
. There exist a strongly mixing system
$\ell \in {\mathbb {N}}$
. There exist a strongly mixing system
![]() $(X,\mathcal A,\mu , (T_g)_{g\in G})$
and homomorphisms
$(X,\mathcal A,\mu , (T_g)_{g\in G})$
and homomorphisms
![]() $\phi _1,\ldots ,\phi _{\ell }:G\rightarrow G$
satisfying (a) for any
$\phi _1,\ldots ,\phi _{\ell }:G\rightarrow G$
satisfying (a) for any
![]() $j\in \{1,\ldots ,\ell \}$
,
$j\in \{1,\ldots ,\ell \}$
,
![]() $\phi _j(G)=G$
, and (b) for any
$\phi _j(G)=G$
, and (b) for any
![]() $i\neq j$
,
$i\neq j$
,
![]() $(\phi _i-\phi _j)(G)=G$
, and such that, for some
$(\phi _i-\phi _j)(G)=G$
, and such that, for some
![]() $A\in \mathcal A$
and some
$A\in \mathcal A$
and some
![]() $\epsilon>0$
, the set
$\epsilon>0$
, the set
![]() $R_{\epsilon }^{\phi _1,\ldots ,\phi _{\ell }}(A,\ldots ,A)$
is not
$R_{\epsilon }^{\phi _1,\ldots ,\phi _{\ell }}(A,\ldots ,A)$
is not
![]() $\Sigma _{\ell }^*$
.
$\Sigma _{\ell }^*$
.
Proof. Let
![]() $(X,\mathcal A,\mu , (T_g)_{g\in G})$
be a strongly mixing system and let
$(X,\mathcal A,\mu , (T_g)_{g\in G})$
be a strongly mixing system and let
![]() $p_1,\ldots ,p_{\ell }\in {\mathbb {N}}$
be
$p_1,\ldots ,p_{\ell }\in {\mathbb {N}}$
be
![]() $\ell $
different prime numbers. For each
$\ell $
different prime numbers. For each
![]() $j\in \{1,\ldots ,\ell \}$
, let
$j\in \{1,\ldots ,\ell \}$
, let
![]() $\phi _j:G\rightarrow G$
be defined by
$\phi _j:G\rightarrow G$
be defined by
It follows that, for any
![]() $j\in \{1,\ldots ,\ell \}$
,
$j\in \{1,\ldots ,\ell \}$
,
![]() $\phi _j(G)=G$
and since, for any distinct
$\phi _j(G)=G$
and since, for any distinct
![]() $i, j\in \{1,\ldots ,\ell \}$
, the sets
$i, j\in \{1,\ldots ,\ell \}$
, the sets
![]() $\{p_i^k\,|\,k\in {\mathbb {N}}\}$
and
$\{p_i^k\,|\,k\in {\mathbb {N}}\}$
and
![]() $\{p_j^k\,|\,k\in {\mathbb {N}}\}$
are disjoint, we have that
$\{p_j^k\,|\,k\in {\mathbb {N}}\}$
are disjoint, we have that
![]() $(\phi _j-\phi _i)(G)=G$
as well.
$(\phi _j-\phi _i)(G)=G$
as well.
Observe that the subgroup
![]() $G'=\{(a_1,0,0,\ldots )\in G\,|\,a_1\in {\mathbb {Z}}\}$
is isomorphic to
$G'=\{(a_1,0,0,\ldots )\in G\,|\,a_1\in {\mathbb {Z}}\}$
is isomorphic to
![]() ${\mathbb {Z}}$
and that, for any
${\mathbb {Z}}$
and that, for any
![]() $j\in \{1,\ldots ,\ell \}$
,
$j\in \{1,\ldots ,\ell \}$
,
![]() $G'\subseteq \ker (\phi _j)$
. Let
$G'\subseteq \ker (\phi _j)$
. Let
![]() $(g_k)_{k\in {\mathbb {N}}}$
be a sequence in
$(g_k)_{k\in {\mathbb {N}}}$
be a sequence in
![]() $G'$
with
$G'$
with
![]() $\lim _{k\rightarrow \infty }g_k=\infty $
. Since, for each
$\lim _{k\rightarrow \infty }g_k=\infty $
. Since, for each
![]() $k\in {\mathbb {N}}$
,
$k\in {\mathbb {N}}$
,
![]() $T_{\phi _j(g_k)}=T_{(0,0,\ldots )}=\text {Id}$
, where
$T_{\phi _j(g_k)}=T_{(0,0,\ldots )}=\text {Id}$
, where
![]() $\text {Id}$
is the identity map on X, we have that, for any
$\text {Id}$
is the identity map on X, we have that, for any
![]() $A\in \mathcal A$
with
$A\in \mathcal A$
with
![]() $\mu (A)\in (0,1)$
, and any
$\mu (A)\in (0,1)$
, and any
![]() $k_1<\cdots <k_{\ell }$
,
$k_1<\cdots <k_{\ell }$
,
It follows that if
![]() $\epsilon $
is small enough, the set
$\epsilon $
is small enough, the set
![]() $R_{\epsilon }^{\phi _1,\ldots ,\phi _{\ell }}(A,\ldots ,A)$
does not intersect the
$R_{\epsilon }^{\phi _1,\ldots ,\phi _{\ell }}(A,\ldots ,A)$
does not intersect the
![]() $\Sigma _{\ell }$
set
$\Sigma _{\ell }$
set
and hence it is not
![]() $\Sigma _{\ell }^*$
. This completes the proof.
$\Sigma _{\ell }^*$
. This completes the proof.
5 Largeness properties of
 $\tilde {\Sigma }_m^*$
sets
$\tilde {\Sigma }_m^*$
sets
As we have seen above, any strongly mixing system
![]() $(X,\mathcal A,\mu ,(T_g)_{g\in G})$
has the property that the sets
$(X,\mathcal A,\mu ,(T_g)_{g\in G})$
has the property that the sets
![]() $R_{\epsilon }(A_0,\ldots ,A_m)$
are
$R_{\epsilon }(A_0,\ldots ,A_m)$
are
![]() $\tilde {\Sigma }_m^*$
(moreover, the strong mixing of
$\tilde {\Sigma }_m^*$
(moreover, the strong mixing of
![]() $(T_g)_{g\in G}$
is characterized by this property). This section is devoted to the discussion of massivity and ubiquity of
$(T_g)_{g\in G}$
is characterized by this property). This section is devoted to the discussion of massivity and ubiquity of
![]() $\tilde {\Sigma }_m^*$
sets. Since strong mixing is a stronger property than those of mild and weak mixing, one should expect that the notions of largeness associated with (multiple) mild and weak mixing are ‘majorized’ by the notion of largeness associated with
$\tilde {\Sigma }_m^*$
sets. Since strong mixing is a stronger property than those of mild and weak mixing, one should expect that the notions of largeness associated with (multiple) mild and weak mixing are ‘majorized’ by the notion of largeness associated with
![]() $\tilde {\Sigma }_m^*$
sets. This will be established in §5.1 and §5.2. Finally, in §5.3 we will show that
$\tilde {\Sigma }_m^*$
sets. This will be established in §5.1 and §5.2. Finally, in §5.3 we will show that
![]() $\tilde {\Sigma }_m^*$
sets are ubiquitous in the sense that they are well spread among the cosets of admissible subgroups of
$\tilde {\Sigma }_m^*$
sets are ubiquitous in the sense that they are well spread among the cosets of admissible subgroups of
![]() $G^m$
(the class of admissible subgroups will be introduced in §5.3).
$G^m$
(the class of admissible subgroups will be introduced in §5.3).
5.1 Any
 $\tilde {\Sigma }_m^*$
set in
$\tilde {\Sigma }_m^*$
set in
 $G^d$
is an
$G^d$
is an
 $\tilde {\text {IP}}^{\mathrm {*}}$
set
$\tilde {\text {IP}}^{\mathrm {*}}$
set
In this section we will introduce
![]() $\tilde {\text {IP}}^{\mathrm {*}}$
sets and juxtapose them with
$\tilde {\text {IP}}^{\mathrm {*}}$
sets and juxtapose them with
![]() $\tilde {\Sigma }_m^*$
sets. (
$\tilde {\Sigma }_m^*$
sets. (
![]() $\tilde {\text {IP}}^{\mathrm {*}}$
sets are intrinsically linked to the multiple mixing properties of mildly mixing systems. The connection between
$\tilde {\text {IP}}^{\mathrm {*}}$
sets are intrinsically linked to the multiple mixing properties of mildly mixing systems. The connection between
![]() $\tilde {\text {IP}}^{\mathrm {*}}$
sets and mildly mixing systems will be addressed in §6.)
$\tilde {\text {IP}}^{\mathrm {*}}$
sets and mildly mixing systems will be addressed in §6.)
Let
![]() $(G,+)$
be a countable abelian group and let
$(G,+)$
be a countable abelian group and let
![]() $\mathcal F$
denote the set of all non-empty finite subsets of
$\mathcal F$
denote the set of all non-empty finite subsets of
![]() ${\mathbb {N}}$
. Given a sequence
${\mathbb {N}}$
. Given a sequence
![]() $(g_k)_{k\in {\mathbb {N}}}$
in G, define an
$(g_k)_{k\in {\mathbb {N}}}$
in G, define an
![]() $\mathcal F$
-sequence
$\mathcal F$
-sequence
![]() $(g_{\alpha })_{\alpha \in \mathcal F}$
by
$(g_{\alpha })_{\alpha \in \mathcal F}$
by
 $$ \begin{align} g_{\alpha}=\sum_{j\in\alpha} g_j=g_{k_1}+\cdots+g_{k_t},\,\alpha=\{k_1,\ldots,k_t\}. \end{align} $$
$$ \begin{align} g_{\alpha}=\sum_{j\in\alpha} g_j=g_{k_1}+\cdots+g_{k_t},\,\alpha=\{k_1,\ldots,k_t\}. \end{align} $$
We will write
if, for every finite
![]() $K\subseteq G$
, there exists an
$K\subseteq G$
, there exists an
![]() $\alpha _0\in \mathcal F$
such that, for any
$\alpha _0\in \mathcal F$
such that, for any
![]() $\alpha \in \mathcal F$
with
$\alpha \in \mathcal F$
with
![]() $\alpha>\alpha _0$
(that is,
$\alpha>\alpha _0$
(that is,
![]() $\min \alpha>\max \alpha _0$
),
$\min \alpha>\max \alpha _0$
),
![]() $g_{\alpha }\not \in K$
.
$g_{\alpha }\not \in K$
.
A set
![]() $E\subseteq G$
is called an IP set if
$E\subseteq G$
is called an IP set if
![]() $E=\{g_{\alpha }\,|\,\alpha \in \mathcal F\}$
for some sequence
$E=\{g_{\alpha }\,|\,\alpha \in \mathcal F\}$
for some sequence
![]() $(g_k)_{k\in {\mathbb {N}}}$
in G such that
$(g_k)_{k\in {\mathbb {N}}}$
in G such that
![]() $\lim _{\alpha \rightarrow \infty }g_{\alpha }=\infty $
. A set
$\lim _{\alpha \rightarrow \infty }g_{\alpha }=\infty $
. A set
![]() $E\subseteq G$
is called IP
$E\subseteq G$
is called IP
![]() $^*$
if it has a non-trivial intersection with every IP set. IP sets are often defined just as sets of the form
$^*$
if it has a non-trivial intersection with every IP set. IP sets are often defined just as sets of the form
(without the requirement that
![]() $\lim _{\alpha \rightarrow \infty }g_{\alpha }=\infty $
). Our choice of definition for IP sets is dictated by our interest in the study of asymptotic properties of measure-preserving actions. The distinction between our definition and the more traditional one is rather mild: for any infinite set of the form
$\lim _{\alpha \rightarrow \infty }g_{\alpha }=\infty $
). Our choice of definition for IP sets is dictated by our interest in the study of asymptotic properties of measure-preserving actions. The distinction between our definition and the more traditional one is rather mild: for any infinite set of the form
![]() $E=\{g_{\alpha }\,|\,\alpha \in \mathcal F\}$
, there exists a sequence
$E=\{g_{\alpha }\,|\,\alpha \in \mathcal F\}$
, there exists a sequence
![]() $(h_k)_{k\in {\mathbb {N}}}$
such that
$(h_k)_{k\in {\mathbb {N}}}$
such that
![]() $\{h_{\alpha }\,|\,\alpha \in \mathcal F\}\subseteq E$
and
$\{h_{\alpha }\,|\,\alpha \in \mathcal F\}\subseteq E$
and
![]() $\lim _{\alpha \rightarrow \infty }h_{\alpha }=\infty $
.
$\lim _{\alpha \rightarrow \infty }h_{\alpha }=\infty $
.
We now introduce modifications of IP and IP
![]() $^*$
sets, namely
$^*$
sets, namely
![]() $\tilde {\text {IP}}$
sets and
$\tilde {\text {IP}}$
sets and
![]() $\tilde {\text {IP}}^{\mathrm {*}}$
sets, which, as will be seen in §6, are naturally linked with the properties of the sets
$\tilde {\text {IP}}^{\mathrm {*}}$
sets, which, as will be seen in §6, are naturally linked with the properties of the sets
![]() $R_{\epsilon }(A_0,\ldots ,A_{\ell })$
in the context of mildly mixing systems.
$R_{\epsilon }(A_0,\ldots ,A_{\ell })$
in the context of mildly mixing systems.
Definition 5.1. Let
![]() $(G,+)$
be a countable abelian group and let
$(G,+)$
be a countable abelian group and let
![]() $d\in {\mathbb {N}}$
. We say that a set
$d\in {\mathbb {N}}$
. We say that a set
![]() $E\subseteq G^d$
is an
$E\subseteq G^d$
is an
![]() $\tilde {\text {IP}}$
set if it is of the form
$\tilde {\text {IP}}$
set if it is of the form
where, for each
![]() $j\in \{1,\ldots ,d\}$
,
$j\in \{1,\ldots ,d\}$
,
![]() $\{g_{\alpha }^{(j)}\,|\,\alpha \in \mathcal F\}$
is generated by
$\{g_{\alpha }^{(j)}\,|\,\alpha \in \mathcal F\}$
is generated by
![]() $(g_{k}^{(j)})_{k\in {\mathbb {N}}}$
as in (5.1) and, in addition, for any
$(g_{k}^{(j)})_{k\in {\mathbb {N}}}$
as in (5.1) and, in addition, for any
![]() $j\in \{1,\ldots ,d\}$
,
$j\in \{1,\ldots ,d\}$
,
and, for any
![]() $i\neq j$
,
$i\neq j$
,
(Note that if
![]() $d=1$
, then
$d=1$
, then
![]() $E\subseteq G$
is an IP set if and only if it is an
$E\subseteq G$
is an IP set if and only if it is an
![]() $\tilde {\text {IP}}$
set.)
$\tilde {\text {IP}}$
set.)
A set
![]() $E\subseteq G^d$
is called an
$E\subseteq G^d$
is called an
![]() $\tilde {\text {IP}}^{\mathrm {*}}$
set if it has a non-trivial intersection with every
$\tilde {\text {IP}}^{\mathrm {*}}$
set if it has a non-trivial intersection with every
![]() $\tilde {\text {IP}}$
set in
$\tilde {\text {IP}}$
set in
![]() $G^d$
.
$G^d$
.
Remark 5.2. Let
![]() $(G,+)$
be a countable abelian group, let
$(G,+)$
be a countable abelian group, let
![]() $d\in {\mathbb {N}}$
and let
$d\in {\mathbb {N}}$
and let
![]() $E\subseteq G^d$
be an
$E\subseteq G^d$
be an
![]() $\tilde {\text {IP}}$
set. From now on, whenever we pick a sequence
$\tilde {\text {IP}}$
set. From now on, whenever we pick a sequence
![]() $(\textbf g_k)_{k\in {\mathbb {N}}}=(g_k^{(1)},\ldots ,g_k^{(d)})_{k\in {\mathbb {N}}}$
in
$(\textbf g_k)_{k\in {\mathbb {N}}}=(g_k^{(1)},\ldots ,g_k^{(d)})_{k\in {\mathbb {N}}}$
in
![]() $G^d$
with the property that
$G^d$
with the property that
![]() $E=\{(g_{\alpha }^{(1)},\ldots ,g_{\alpha }^{(d)})\,|\,\alpha \in \mathcal F\}$
, we will tacitly assume that
$E=\{(g_{\alpha }^{(1)},\ldots ,g_{\alpha }^{(d)})\,|\,\alpha \in \mathcal F\}$
, we will tacitly assume that
![]() $(g_k^{(1)})_{k\in {\mathbb {N}}},\ldots,$
$(g_k^{(1)})_{k\in {\mathbb {N}}},\ldots,$
![]() $(g_k^{(d)})_{k\in {\mathbb {N}}}$
satisfy (5.2) and (5.3).
$(g_k^{(d)})_{k\in {\mathbb {N}}}$
satisfy (5.2) and (5.3).
The following lemma unveils an important connection between
![]() $\tilde {\text {IP}}$
and
$\tilde {\text {IP}}$
and
![]() $\tilde {\Sigma }_m$
sets.
$\tilde {\Sigma }_m$
sets.
Lemma 5.3. Let
![]() $(G,+)$
be a countable abelian group and let
$(G,+)$
be a countable abelian group and let
![]() $d,m\in {\mathbb {N}}$
. Any
$d,m\in {\mathbb {N}}$
. Any
![]() $\tilde {\text {IP}}$
set
$\tilde {\text {IP}}$
set
![]() $E\subseteq G^d$
contains a
$E\subseteq G^d$
contains a
![]() $\tilde {\Sigma }_m$
set. Namely, there exist non-degenerated and essentially distinct sequences
$\tilde {\Sigma }_m$
set. Namely, there exist non-degenerated and essentially distinct sequences
in
![]() $G^m$
with the property that
$G^m$
with the property that
![]() $\{(g_{\alpha }^{(1)},\ldots ,g_{\alpha }^{(d)})\,|\,\alpha \in {\mathbb {N}}^{(m)}\}\subseteq E$
, where, for each
$\{(g_{\alpha }^{(1)},\ldots ,g_{\alpha }^{(d)})\,|\,\alpha \in {\mathbb {N}}^{(m)}\}\subseteq E$
, where, for each
![]() $j\in \{1,\ldots ,d\}$
and each
$j\in \{1,\ldots ,d\}$
and each
![]() $\alpha =\{k_1,\ldots ,k_m\}\in {\mathbb {N}}^{(m)}$
,
$\alpha =\{k_1,\ldots ,k_m\}\in {\mathbb {N}}^{(m)}$
,
![]() $g_{\alpha }^{(j)}=g_{k_1,1}^{(j)}+\cdots +g_{k_m,m}^{(j)}$
.
$g_{\alpha }^{(j)}=g_{k_1,1}^{(j)}+\cdots +g_{k_m,m}^{(j)}$
.
Proof. Let E be an
![]() $\tilde {\text {IP}}$
set and let
$\tilde {\text {IP}}$
set and let
![]() $(\textbf h_k)_{k\in {\mathbb {N}}}= (h_k^{(1)},\ldots ,h_k^{(d)})_{k\in {\mathbb {N}}}$
be such that
$(\textbf h_k)_{k\in {\mathbb {N}}}= (h_k^{(1)},\ldots ,h_k^{(d)})_{k\in {\mathbb {N}}}$
be such that
Following the stipulation made in Remark 5.2, for any finite set
![]() $F\subseteq G$
, we can find an
$F\subseteq G$
, we can find an
![]() $\alpha _F\in \mathcal F$
such that, for any
$\alpha _F\in \mathcal F$
such that, for any
![]() $\alpha \in \mathcal F$
with
$\alpha \in \mathcal F$
with
![]() $\alpha> \alpha _F$
and any distinct
$\alpha> \alpha _F$
and any distinct
![]() $i,j\in \{1,\ldots d\}$
,
$i,j\in \{1,\ldots d\}$
,
![]() $h^{(j)}_{\alpha }\not \in F$
and
$h^{(j)}_{\alpha }\not \in F$
and
![]() $(h^{(j)}_{\alpha }-h^{(i)}_{\alpha })\not \in F$
. In particular, for any distinct
$(h^{(j)}_{\alpha }-h^{(i)}_{\alpha })\not \in F$
. In particular, for any distinct
![]() $i,j\in \{1,\ldots ,d\}$
,
$i,j\in \{1,\ldots ,d\}$
,
For each
![]() $j\in \{1,\ldots ,d\}$
and each
$j\in \{1,\ldots ,d\}$
and each
![]() $k\in {\mathbb {N}}$
, we let
$k\in {\mathbb {N}}$
, we let
 $$ \begin{align} \textbf g_k^{(j)}=\underbrace{(h_{k}^{(j)},\ldots,h_{k}^{(j)})}_{m\text{ times}}. \end{align} $$
$$ \begin{align} \textbf g_k^{(j)}=\underbrace{(h_{k}^{(j)},\ldots,h_{k}^{(j)})}_{m\text{ times}}. \end{align} $$
Note that, by (5.4), the sequences
![]() $(\textbf g^{(1)}_k)_{k\in {\mathbb {N}}},\ldots,$
$(\textbf g^{(1)}_k)_{k\in {\mathbb {N}}},\ldots,$
![]() $(\textbf g^{(d)}_k)_{k\in {\mathbb {N}}}$
are non-degenerated and essentially distinct. It follows now from (5.5) that, for any
$(\textbf g^{(d)}_k)_{k\in {\mathbb {N}}}$
are non-degenerated and essentially distinct. It follows now from (5.5) that, for any
![]() $\alpha =\{k_1,\ldots ,k_m\}\in {\mathbb {N}}^{(m)}$
,
$\alpha =\{k_1,\ldots ,k_m\}\in {\mathbb {N}}^{(m)}$
,
 $$ \begin{align*}(g^{(1)}_{\alpha},\ldots,g^{(d)}_{\alpha})=\bigg(\sum_{j=1}^m h_{k_j}^{(1)},\ldots,\sum_{j=1}^m h_{k_j}^{(d)}\bigg)=\bigg(h_{\{k_1,\ldots,k_m\}}^{(1)},\ldots,h_{\{k_1,\ldots,k_m\}}^{(d)}\bigg)\in E,\end{align*} $$
$$ \begin{align*}(g^{(1)}_{\alpha},\ldots,g^{(d)}_{\alpha})=\bigg(\sum_{j=1}^m h_{k_j}^{(1)},\ldots,\sum_{j=1}^m h_{k_j}^{(d)}\bigg)=\bigg(h_{\{k_1,\ldots,k_m\}}^{(1)},\ldots,h_{\{k_1,\ldots,k_m\}}^{(d)}\bigg)\in E,\end{align*} $$
which completes the proof.
Remark 5.4. The proof of Lemma 5.3 actually shows that any
![]() $\tilde {\text {IP}}$
set is a union of
$\tilde {\text {IP}}$
set is a union of
![]() $\tilde {\Sigma }_t$
sets. Let
$\tilde {\Sigma }_t$
sets. Let
![]() $E\subseteq G^d$
be an
$E\subseteq G^d$
be an
![]() $\tilde {\text {IP}}$
set and let
$\tilde {\text {IP}}$
set and let
![]() $(\textbf g_k)_{k\in {\mathbb {N}}}$
be a sequence such that
$(\textbf g_k)_{k\in {\mathbb {N}}}$
be a sequence such that
![]() $E=\{\textbf g_{\alpha }\,|\alpha \in \mathcal F\}$
. The proof of Lemma 5.3 shows that, for each
$E=\{\textbf g_{\alpha }\,|\alpha \in \mathcal F\}$
. The proof of Lemma 5.3 shows that, for each
![]() $t\in {\mathbb {N}}$
,
$t\in {\mathbb {N}}$
,
![]() $\{\textbf g_{k_1}+\cdots +\textbf g_{k_t}\,|\,k_1<\cdots <k_t\}$
is a
$\{\textbf g_{k_1}+\cdots +\textbf g_{k_t}\,|\,k_1<\cdots <k_t\}$
is a
![]() $\tilde {\Sigma }_t$
set. Hence,
$\tilde {\Sigma }_t$
set. Hence,
As an immediate consequence of Lemma 5.3 we have the following result.
Corollary 5.5. Let
![]() $(G,+)$
be a countable abelian group and let
$(G,+)$
be a countable abelian group and let
![]() $d,m\in {\mathbb {N}}$
. Every
$d,m\in {\mathbb {N}}$
. Every
![]() $\tilde \Sigma _m^*$
set in
$\tilde \Sigma _m^*$
set in
![]() $G^d$
is an
$G^d$
is an
![]() $\tilde {\text {IP}}^{\mathrm {*}}$
set.
$\tilde {\text {IP}}^{\mathrm {*}}$
set.
Proof. Let
![]() $E\subseteq G^d$
be a
$E\subseteq G^d$
be a
![]() $\tilde {\Sigma }_m^*$
set and let
$\tilde {\Sigma }_m^*$
set and let
![]() $D\subseteq G^d$
be an
$D\subseteq G^d$
be an
![]() $\tilde {\text {IP}}$
set. By Lemma 5.3, we have that D contains a
$\tilde {\text {IP}}$
set. By Lemma 5.3, we have that D contains a
![]() $\tilde {\Sigma }_m$
set and hence
$\tilde {\Sigma }_m$
set and hence
![]() $E\cap D\neq \emptyset $
. Since D was arbitrary, this shows that E is an
$E\cap D\neq \emptyset $
. Since D was arbitrary, this shows that E is an
![]() $\tilde {\text {IP}}^{\mathrm {*}}$
set.
$\tilde {\text {IP}}^{\mathrm {*}}$
set.
5.2 Any
 $\tilde {\Sigma }_m^*$
set in
$\tilde {\Sigma }_m^*$
set in
 $G^d$
has uniform density one
$G^d$
has uniform density one
We start with defining the notions of upper density and uniform density one in countable abelian groups.
Definition 5.6. Let
![]() $(G,+)$
be a countable abelian group, let
$(G,+)$
be a countable abelian group, let
![]() $E\subseteq G$
and let
$E\subseteq G$
and let
![]() $(F_k)_{k\in {\mathbb {N}}}$
be a Følner sequence in G. (A sequence
$(F_k)_{k\in {\mathbb {N}}}$
be a Følner sequence in G. (A sequence
![]() $(F_k)_{k\in {\mathbb {N}}}$
of non-empty finite subsets of G is a Følner sequence if, for any
$(F_k)_{k\in {\mathbb {N}}}$
of non-empty finite subsets of G is a Følner sequence if, for any
![]() $g\in G$
,
$g\in G$
,
where, for a finite set A,
![]() $|A|$
denotes its cardinality. It is well known that every countable abelian group contains a Følner sequence.) The upper density of E with respect to
$|A|$
denotes its cardinality. It is well known that every countable abelian group contains a Følner sequence.) The upper density of E with respect to
![]() $(F_k)_{k\in {\mathbb {N}}}$
is defined by
$(F_k)_{k\in {\mathbb {N}}}$
is defined by
A set
![]() $E\subseteq G$
has uniform density one if, for every Følner sequence
$E\subseteq G$
has uniform density one if, for every Følner sequence
![]() $(F_k)_{k\in {\mathbb {N}}}$
,
$(F_k)_{k\in {\mathbb {N}}}$
,
![]() $\overline d_{(F_k)}(E)=1$
.
$\overline d_{(F_k)}(E)=1$
.
Sets of uniform density one are intrinsically connected with weakly mixing measure-preserving systems. Recall that a measure-preserving action
![]() $(T_g)_{g\in G}$
on a probability space
$(T_g)_{g\in G}$
on a probability space
![]() $(X,\mathcal A,\mu )$
is called weakly mixing if the diagonal action
$(X,\mathcal A,\mu )$
is called weakly mixing if the diagonal action
![]() $(T_g\times T_g)_{g\in G}$
on
$(T_g\times T_g)_{g\in G}$
on
![]() $X\times X$
is ergodic. When G is an amenable group, the notion of weak mixing can be equivalently defined with the help of strong Césaro limits along Følner sequences. Namely,
$X\times X$
is ergodic. When G is an amenable group, the notion of weak mixing can be equivalently defined with the help of strong Césaro limits along Følner sequences. Namely,
![]() $(T_g)_{g\in G}$
is weakly mixing if and only if, for any Følner sequence
$(T_g)_{g\in G}$
is weakly mixing if and only if, for any Følner sequence
![]() $(F_k)_{k\in {\mathbb {N}}}$
and any
$(F_k)_{k\in {\mathbb {N}}}$
and any
![]() $A_0,A_1\in \mathcal A$
,
$A_0,A_1\in \mathcal A$
,
 $$ \begin{align*}\lim_{k\rightarrow\infty}\frac{1}{|F_k|}\sum_{g\in F_k}|\mu(A_0\cap T_gA_1)-\mu(A_0)\mu(A_1)|=0.\end{align*} $$
$$ \begin{align*}\lim_{k\rightarrow\infty}\frac{1}{|F_k|}\sum_{g\in F_k}|\mu(A_0\cap T_gA_1)-\mu(A_0)\mu(A_1)|=0.\end{align*} $$
It follows that
![]() $(T_g)_{g\in G}$
is weakly mixing if and only if the sets
$(T_g)_{g\in G}$
is weakly mixing if and only if the sets
have uniform density one. The reader will find a few more equivalent forms of weak mixing in Proposition 6.8 below.
In order to derive the main result of this subsection, namely the fact that every
![]() $\tilde {\Sigma }_m^*$
set has uniform density one, we need first to prove two auxiliary propositions.
$\tilde {\Sigma }_m^*$
set has uniform density one, we need first to prove two auxiliary propositions.
Proposition 5.7. Let
![]() $(G,+)$
be a countable abelian group, let
$(G,+)$
be a countable abelian group, let
![]() $d\in {\mathbb {N}}$
and let
$d\in {\mathbb {N}}$
and let
![]() $(F_k)_{k\in {\mathbb {N}}}$
be a Følner sequence in
$(F_k)_{k\in {\mathbb {N}}}$
be a Følner sequence in
![]() $G^d$
. For any
$G^d$
. For any
![]() $E\subseteq G^d$
with
$E\subseteq G^d$
with
![]() $\overline d_{(F_k)}(E)>0$
and any
$\overline d_{(F_k)}(E)>0$
and any
![]() $\tilde {\text {IP}}$
set
$\tilde {\text {IP}}$
set
![]() $D\subseteq G^d$
, there exists a sequence
$D\subseteq G^d$
, there exists a sequence
![]() $(\textbf g_k)_{k\in {\mathbb {N}}}=(g_k^{(1)},\ldots ,g_k^{(d)})$
in
$(\textbf g_k)_{k\in {\mathbb {N}}}=(g_k^{(1)},\ldots ,g_k^{(d)})$
in
![]() $G^d$
such that (a)
$G^d$
such that (a)
![]() $\{\textbf g_{\alpha }\,|\,\alpha \in \mathcal F\}\subseteq D$
, (b) for any distinct
$\{\textbf g_{\alpha }\,|\,\alpha \in \mathcal F\}\subseteq D$
, (b) for any distinct
![]() $i,j\in \{1,\ldots ,d\}$
, (5.2) and (5.3) hold, and (c) for any
$i,j\in \{1,\ldots ,d\}$
, (5.2) and (5.3) hold, and (c) for any
![]() $\alpha \in \mathcal F$
,
$\alpha \in \mathcal F$
,
 $$ \begin{align} \overline d_{(F_k)}\bigg(\bigcap_{\beta\subseteq\alpha,\,\beta\neq\emptyset}(E-\textbf g_{\beta})\bigg)>0. \end{align} $$
$$ \begin{align} \overline d_{(F_k)}\bigg(\bigcap_{\beta\subseteq\alpha,\,\beta\neq\emptyset}(E-\textbf g_{\beta})\bigg)>0. \end{align} $$
In other words, for each
![]() $\alpha \in \mathcal F$
, the set
$\alpha \in \mathcal F$
, the set
![]() $E_{\alpha }=\{\textbf h\in G^d\,|\,\text { for all } \beta \subseteq \alpha ,\,\beta \neq \emptyset ,\, \textbf h+ \textbf g_{\beta }\in E\}$
satisfies
$E_{\alpha }=\{\textbf h\in G^d\,|\,\text { for all } \beta \subseteq \alpha ,\,\beta \neq \emptyset ,\, \textbf h+ \textbf g_{\beta }\in E\}$
satisfies
![]() $\overline d_{(F_k)}(E_{\alpha })>0$
.
$\overline d_{(F_k)}(E_{\alpha })>0$
.
Proof. Let
![]() $D=\{\textbf h_{\alpha }\,|\,\alpha \in \mathcal F\}$
be an
$D=\{\textbf h_{\alpha }\,|\,\alpha \in \mathcal F\}$
be an
![]() $\tilde {\text {IP}}$
set in
$\tilde {\text {IP}}$
set in
![]() $G^d$
generated by the sequence
$G^d$
generated by the sequence
![]() $(\textbf h_k)_{k\in {\mathbb {N}}}=(h_{k,1},\ldots ,h_{k,d})_{k\in {\mathbb {N}}}$
. We claim that, for any
$(\textbf h_k)_{k\in {\mathbb {N}}}=(h_{k,1},\ldots ,h_{k,d})_{k\in {\mathbb {N}}}$
. We claim that, for any
![]() $M\in {\mathbb {N}}$
with
$M\in {\mathbb {N}}$
with
![]() $M>{1}/{\overline d_{(F_k)}(E)}$
, there exist
$M>{1}/{\overline d_{(F_k)}(E)}$
, there exist
![]() $L,R\in {\mathbb {N}}$
,
$L,R\in {\mathbb {N}}$
,
![]() $L<R\leq M$
, for which
$L<R\leq M$
, for which
![]() $\overline d_{(F_k)}(E\cap (E-\textbf h_{\{L+1,L+2,\ldots ,R\}}))>0$
. To see this, suppose for the sake of contradiction that, for any distinct
$\overline d_{(F_k)}(E\cap (E-\textbf h_{\{L+1,L+2,\ldots ,R\}}))>0$
. To see this, suppose for the sake of contradiction that, for any distinct
![]() $R,L\in \{1,\ldots ,M\}$
,
$R,L\in \{1,\ldots ,M\}$
,
![]() $R>L$
,
$R>L$
,
![]() $\overline d_{(F_k)}(E\cap (E-\textbf h_{\{L+1,\ldots ,R\}}))=0$
. Since
$\overline d_{(F_k)}(E\cap (E-\textbf h_{\{L+1,\ldots ,R\}}))=0$
. Since
![]() $\overline d_{(F_k)}$
is translation invariant and for any
$\overline d_{(F_k)}$
is translation invariant and for any
![]() $L,R\in \{1,\ldots ,M\}$
,
$L,R\in \{1,\ldots ,M\}$
,
![]() $L<R$
,
$L<R$
,
![]() $\textbf h_{\{L+1,\ldots ,R\}}=\textbf h_{\{1,\ldots ,R\}}-\textbf h_{\{1,\ldots ,L\}}$
, we have that
$\textbf h_{\{L+1,\ldots ,R\}}=\textbf h_{\{1,\ldots ,R\}}-\textbf h_{\{1,\ldots ,L\}}$
, we have that
It follows that
 $$ \begin{align*}\overline d_{(F_k)}\bigg(\bigcup_{R=1}^M (E-\textbf h_{\{1,\ldots,R\}})\bigg)=\sum_{R=1}^M\overline d_{(F_k)}(E-\textbf h_{\{1,\ldots,R\}})=M\overline d_{(F_k)}(E)>1,\end{align*} $$
$$ \begin{align*}\overline d_{(F_k)}\bigg(\bigcup_{R=1}^M (E-\textbf h_{\{1,\ldots,R\}})\bigg)=\sum_{R=1}^M\overline d_{(F_k)}(E-\textbf h_{\{1,\ldots,R\}})=M\overline d_{(F_k)}(E)>1,\end{align*} $$
a contradiction. Thus, there exist
![]() $L,R\in {\mathbb {N}}$
with
$L,R\in {\mathbb {N}}$
with
![]() $L<R\leq M$
such that
$L<R\leq M$
such that
![]() $\overline d_{(F_k)}(E\cap (E-\textbf h_{\{L+1,\ldots ,R\}}))>0$
. We will let
$\overline d_{(F_k)}(E\cap (E-\textbf h_{\{L+1,\ldots ,R\}}))>0$
. We will let
![]() $\gamma _1=\{L+1,\ldots ,,R\}$
.
$\gamma _1=\{L+1,\ldots ,,R\}$
.
Now let
![]() $E_1=E\cap (E-\textbf h_{\gamma _1})$
. Repeating the above argument, we find
$E_1=E\cap (E-\textbf h_{\gamma _1})$
. Repeating the above argument, we find
![]() $L',R'\in {\mathbb {N}}$
,
$L',R'\in {\mathbb {N}}$
,
![]() $R<L'<R'$
, such that
$R<L'<R'$
, such that
![]() $\gamma _2=\{L'+1,\ldots ,R'\}$
satisfies
$\gamma _2=\{L'+1,\ldots ,R'\}$
satisfies
![]() $\overline d_{(F_k)}(E_1\cap (E_1-\textbf h_{\gamma _2}))>0$
. It follows that
$\overline d_{(F_k)}(E_1\cap (E_1-\textbf h_{\gamma _2}))>0$
. It follows that
![]() $\gamma _1<\gamma _2$
and that
$\gamma _1<\gamma _2$
and that
![]() $\textbf h_{\gamma _1\cup \gamma _2}=\textbf h_{\gamma _1}+\textbf h_{\gamma _2}$
. Hence,
$\textbf h_{\gamma _1\cup \gamma _2}=\textbf h_{\gamma _1}+\textbf h_{\gamma _2}$
. Hence,
Continuing in this way, we can find a sequence
![]() $(\gamma _k)_{k\in {\mathbb {N}}}$
with
$(\gamma _k)_{k\in {\mathbb {N}}}$
with
![]() $\gamma _k<\gamma _{k+1}$
for each
$\gamma _k<\gamma _{k+1}$
for each
![]() $k\in {\mathbb {N}}$
and the property that, for any
$k\in {\mathbb {N}}$
and the property that, for any
![]() $\alpha \in \mathcal F$
,
$\alpha \in \mathcal F$
,
 $$ \begin{align*}\overline d_{(F_k)}\bigg(\bigcap_{\beta\subseteq\alpha,\,\beta\neq\emptyset}(E-\textbf h_{\bigcup_{k\in\beta}\gamma_k})\bigg)>0.\end{align*} $$
$$ \begin{align*}\overline d_{(F_k)}\bigg(\bigcap_{\beta\subseteq\alpha,\,\beta\neq\emptyset}(E-\textbf h_{\bigcup_{k\in\beta}\gamma_k})\bigg)>0.\end{align*} $$
For each
![]() $k\in {\mathbb {N}}$
, let
$k\in {\mathbb {N}}$
, let
![]() $\textbf g_k=\textbf h_{\gamma _k}$
and, for each
$\textbf g_k=\textbf h_{\gamma _k}$
and, for each
![]() $\alpha \in \mathcal F$
, let
$\alpha \in \mathcal F$
, let
![]() $\textbf g_{\alpha }=\sum _{j\in \alpha }\textbf g_j=\textbf h_{\bigcup _{j\in \alpha }\gamma _j}$
. Observe that the sequence
$\textbf g_{\alpha }=\sum _{j\in \alpha }\textbf g_j=\textbf h_{\bigcup _{j\in \alpha }\gamma _j}$
. Observe that the sequence
![]() $(\textbf g_{\alpha })_{\alpha \in \mathcal F}$
satisfies (5.6). Let
$(\textbf g_{\alpha })_{\alpha \in \mathcal F}$
satisfies (5.6). Let
![]() $D'=\{\textbf g_{\alpha }\,|\,\alpha \in \mathcal F\}$
. Clearly
$D'=\{\textbf g_{\alpha }\,|\,\alpha \in \mathcal F\}$
. Clearly
![]() $D'\subseteq D$
. To finish the proof observe that
$D'\subseteq D$
. To finish the proof observe that
satisfies (5.2) and (5.3). Indeed, in view of Remark 5.2, for any
![]() $j\in \{1,\ldots ,d\}$
,
$j\in \{1,\ldots ,d\}$
,
and, for
![]() $i\neq j$
,
$i\neq j$
,
Proposition 5.8. Let
![]() $(G,+)$
be a countable abelian group, let
$(G,+)$
be a countable abelian group, let
![]() $d,m\in {\mathbb {N}}$
and let
$d,m\in {\mathbb {N}}$
and let
![]() $(F_k)_{k\in {\mathbb {N}}}$
be a Følner sequence in
$(F_k)_{k\in {\mathbb {N}}}$
be a Følner sequence in
![]() $G^d$
. Any
$G^d$
. Any
![]() $E\subseteq G^d$
with
$E\subseteq G^d$
with
![]() $\overline d_{(F_k)}(E)>0$
contains a
$\overline d_{(F_k)}(E)>0$
contains a
![]() $\tilde {\Sigma }_m$
set. Namely, there exist non-degenerated and essentially distinct sequences
$\tilde {\Sigma }_m$
set. Namely, there exist non-degenerated and essentially distinct sequences
in
![]() $G^m$
with the property that
$G^m$
with the property that
![]() $\{(g_{\alpha }^{(1)},\ldots ,g_{\alpha }^{(d)})\,|\,\alpha \in {\mathbb {N}}^{(m)}\}\subseteq E$
.
$\{(g_{\alpha }^{(1)},\ldots ,g_{\alpha }^{(d)})\,|\,\alpha \in {\mathbb {N}}^{(m)}\}\subseteq E$
.
Proof. Fix
![]() $d\in {\mathbb {N}}$
and let D be an
$d\in {\mathbb {N}}$
and let D be an
![]() $\tilde {\text {IP}}$
set in
$\tilde {\text {IP}}$
set in
![]() $G^d$
. Let
$G^d$
. Let
![]() $(\textbf h_k)_{k\in {\mathbb {N}}}=(h_k^{(1)},\ldots ,h_k^{(d)})_{k\in {\mathbb {N}}}$
be a sequence in
$(\textbf h_k)_{k\in {\mathbb {N}}}=(h_k^{(1)},\ldots ,h_k^{(d)})_{k\in {\mathbb {N}}}$
be a sequence in
![]() $G^d$
with
$G^d$
with
![]() $D=\{\textbf h_{\alpha }\,|\,\alpha \in \mathcal F\}$
. Invoking Proposition 5.7 and passing, if needed, to a sub-
$D=\{\textbf h_{\alpha }\,|\,\alpha \in \mathcal F\}$
. Invoking Proposition 5.7 and passing, if needed, to a sub-
![]() $\tilde {\text {IP}}$
set in D, we can assume that, for any
$\tilde {\text {IP}}$
set in D, we can assume that, for any
![]() $\alpha \in \mathcal F$
,
$\alpha \in \mathcal F$
,
 $$ \begin{align} \overline d_{(F_k)}\bigg(\bigcap_{\beta\subseteq\alpha,\,\beta\neq\emptyset}(E-\textbf h_{\beta})\bigg)>0 \end{align} $$
$$ \begin{align} \overline d_{(F_k)}\bigg(\bigcap_{\beta\subseteq\alpha,\,\beta\neq\emptyset}(E-\textbf h_{\beta})\bigg)>0 \end{align} $$
and that
![]() $(\textbf h_k)_{k\in {\mathbb {N}}}$
satisfies (5.2) and (5.3).
$(\textbf h_k)_{k\in {\mathbb {N}}}$
satisfies (5.2) and (5.3).
Let
![]() $m=1$
. There exists a sequence
$m=1$
. There exists a sequence
![]() $(\alpha _k)_{k\in {\mathbb {N}}}$
in
$(\alpha _k)_{k\in {\mathbb {N}}}$
in
![]() $\mathcal F$
such that, for each
$\mathcal F$
such that, for each
![]() $k\in {\mathbb {N}}$
,
$k\in {\mathbb {N}}$
,
![]() $ \alpha _k<\alpha _{k+1}$
and such that, for any distinct
$ \alpha _k<\alpha _{k+1}$
and such that, for any distinct
![]() $k,k'\in {\mathbb {N}}$
and any distinct
$k,k'\in {\mathbb {N}}$
and any distinct
![]() $i,j\in \{1,\ldots ,d\}$
,
$i,j\in \{1,\ldots ,d\}$
,
Pick a sequence
![]() $(A_k)_{k\in {\mathbb {N}}}$
of finite subsets of G with the properties that, for each
$(A_k)_{k\in {\mathbb {N}}}$
of finite subsets of G with the properties that, for each
![]() $k\in {\mathbb {N}}$
, (a)
$k\in {\mathbb {N}}$
, (a)
![]() $|A_k|=k$
, (b)
$|A_k|=k$
, (b)
![]() $A_k\subseteq A_{k+1}$
, and (c)
$A_k\subseteq A_{k+1}$
, and (c)
![]() $\bigcup _{k\in {\mathbb {N}}} A_k=G$
. By (5.7), for each
$\bigcup _{k\in {\mathbb {N}}} A_k=G$
. By (5.7), for each
![]() $k\in {\mathbb {N}}$
we can find
$k\in {\mathbb {N}}$
we can find
![]() $\textbf b_k=(b_{k,1},\ldots ,b_{k,d})$
in
$\textbf b_k=(b_{k,1},\ldots ,b_{k,d})$
in
![]() $G^d$
such that, for any
$G^d$
such that, for any
![]() $t\in \{1,\ldots ,kd^2+1\}$
,
$t\in \{1,\ldots ,kd^2+1\}$
,
![]() $\textbf b_k+\textbf h_{\alpha _t}\in E$
. By (5.8), for any
$\textbf b_k+\textbf h_{\alpha _t}\in E$
. By (5.8), for any
![]() $k\in {\mathbb {N}}$
and any
$k\in {\mathbb {N}}$
and any
![]() $j\in \{1,\ldots ,d\}$
, there exist at most k natural numbers t for which
$j\in \{1,\ldots ,d\}$
, there exist at most k natural numbers t for which
![]() $b_{k,j}+h_{\alpha _t}^{(j)}\in A_k$
. Similarly, for any distinct
$b_{k,j}+h_{\alpha _t}^{(j)}\in A_k$
. Similarly, for any distinct
![]() $i,j\in \{1,\ldots ,d\}$
, one has
$i,j\in \{1,\ldots ,d\}$
, one has
![]() $(b_{k,j}-b_{k,i})+(h_{\alpha _t}^{(j)}-h_{\alpha _t}^{(i)})\in A_k$
for at most k natural numbers t.
$(b_{k,j}-b_{k,i})+(h_{\alpha _t}^{(j)}-h_{\alpha _t}^{(i)})\in A_k$
for at most k natural numbers t.
We claim that there exists
![]() $t\in \{1,\ldots ,kd^2+1\}$
such that, for any
$t\in \{1,\ldots ,kd^2+1\}$
such that, for any
![]() $j\in \{1,\ldots ,d\}$
,
$j\in \{1,\ldots ,d\}$
,
![]() $b_{k,j}+h_{\alpha _t}^{(j)}\not \in A_k$
and, for any
$b_{k,j}+h_{\alpha _t}^{(j)}\not \in A_k$
and, for any
![]() $i\neq j$
,
$i\neq j$
,
![]() $(b_{k,j}-b_{k,i})+(h_{\alpha _t}^{(j)}-h_{\alpha _t}^{(i)})\not \in A_k$
. Suppose for contradiction that this is not the case. Since there are
$(b_{k,j}-b_{k,i})+(h_{\alpha _t}^{(j)}-h_{\alpha _t}^{(i)})\not \in A_k$
. Suppose for contradiction that this is not the case. Since there are
![]() $d^2-d$
pairs
$d^2-d$
pairs
![]() $(i,j)$
with distinct
$(i,j)$
with distinct
![]() $i, j\in \{1,\ldots ,d\}$
, there exist at least
$i, j\in \{1,\ldots ,d\}$
, there exist at least
![]() $k+1$
natural numbers t for which, say,
$k+1$
natural numbers t for which, say,
![]() $b_{k,1}+h_{\alpha _t}^{(1)}\in A_k$
, a contradiction.
$b_{k,1}+h_{\alpha _t}^{(1)}\in A_k$
, a contradiction.
Thus, there exists a sequence
![]() $(k_t)_{t\in {\mathbb {N}}}$
in
$(k_t)_{t\in {\mathbb {N}}}$
in
![]() ${\mathbb {N}}$
for which the sequences
${\mathbb {N}}$
for which the sequences
are non-degenerated and essentially distinct, and
Now let
![]() $m>1$
. By Lemma 5.3 there exist non-degenerated and essentially distinct sequences
$m>1$
. By Lemma 5.3 there exist non-degenerated and essentially distinct sequences
![]() $(\textbf f_k^{(j)})_{k\in {\mathbb {N}}}=(f^{(j)}_{k,1},\ldots ,f^{(j)}_{k,m-1})_{k\in {\mathbb {N}}}$
,
$(\textbf f_k^{(j)})_{k\in {\mathbb {N}}}=(f^{(j)}_{k,1},\ldots ,f^{(j)}_{k,m-1})_{k\in {\mathbb {N}}}$
,
![]() $j\in \{1,\ldots ,d\}$
, with the property that
$j\in \{1,\ldots ,d\}$
, with the property that
![]() $\{(f^{(1)}_{\alpha },\ldots ,f^{(d)}_{\alpha })\,|\,\alpha \in {\mathbb {N}}^{(m-1)}\}\subseteq D$
. For each
$\{(f^{(1)}_{\alpha },\ldots ,f^{(d)}_{\alpha })\,|\,\alpha \in {\mathbb {N}}^{(m-1)}\}\subseteq D$
. For each
![]() $k\in {\mathbb {N}}$
, let
$k\in {\mathbb {N}}$
, let
By (5.7), for each
![]() $k\in {\mathbb {N}}$
,
$k\in {\mathbb {N}}$
,
![]() $\overline d_{(F_k)}(E_k)>0$
. It follows from the case
$\overline d_{(F_k)}(E_k)>0$
. It follows from the case
![]() $m=1$
that there exist sequences
$m=1$
that there exist sequences
with the properties that (a) for any
![]() $k\in {\mathbb {N}}$
,
$k\in {\mathbb {N}}$
,
![]() $(g_{k,1},\ldots ,g_{k,d})\in E_k$
, (b) for any
$(g_{k,1},\ldots ,g_{k,d})\in E_k$
, (b) for any
![]() $j\in \{1,\ldots ,d\}$
,
$j\in \{1,\ldots ,d\}$
,
![]() $\lim _{k\rightarrow \infty }g_{k,j}=\infty $
, and (c) for any distinct
$\lim _{k\rightarrow \infty }g_{k,j}=\infty $
, and (c) for any distinct
![]() $i,j\in \{1,\ldots ,d\}$
,
$i,j\in \{1,\ldots ,d\}$
,
![]() $\lim _{k\rightarrow \infty }g_{k,i}-g_{k,j}=\infty $
. For each
$\lim _{k\rightarrow \infty }g_{k,i}-g_{k,j}=\infty $
. For each
![]() $j\in \{1,\ldots ,d\}$
, form the sequence
$j\in \{1,\ldots ,d\}$
, form the sequence
By (5.9) and (a), we have that, for any
![]() $k\in {\mathbb {N}}$
and any
$k\in {\mathbb {N}}$
and any
![]() $\alpha \subseteq \{1,\ldots ,k-1\}$
with
$\alpha \subseteq \{1,\ldots ,k-1\}$
with
![]() $|\alpha |=m-1$
,
$|\alpha |=m-1$
,
![]() $(g_{k,1},\ldots ,g_{k,d})+(f^{(1)}_{\alpha },\ldots ,f^{(d)}_{\alpha })\in E$
and hence
$(g_{k,1},\ldots ,g_{k,d})+(f^{(1)}_{\alpha },\ldots ,f^{(d)}_{\alpha })\in E$
and hence
By (b) and (c), the sequences
![]() $(\textbf g_k^{(1)})_{k\in {\mathbb {N}}},\ldots,$
$(\textbf g_k^{(1)})_{k\in {\mathbb {N}}},\ldots,$
![]() $(\textbf g_k^{(d)})_{k\in {\mathbb {N}}}$
are non-degenerated and essentially distinct. We are done.
$(\textbf g_k^{(d)})_{k\in {\mathbb {N}}}$
are non-degenerated and essentially distinct. We are done.
Corollary 5.9. Let
![]() $(G,+)$
be a countable abelian group and let
$(G,+)$
be a countable abelian group and let
![]() $d,m\in {\mathbb {N}}$
. Every
$d,m\in {\mathbb {N}}$
. Every
![]() $\tilde \Sigma _m^*$
set in
$\tilde \Sigma _m^*$
set in
![]() $G^d$
has uniform density one.
$G^d$
has uniform density one.
Proof. We will assume that
![]() $D\subseteq G^d$
does not have uniform density one and show that D is not a
$D\subseteq G^d$
does not have uniform density one and show that D is not a
![]() $\tilde {\Sigma }_m^*$
set. Indeed, if D does not have uniform density one, then there exists a Følner sequence
$\tilde {\Sigma }_m^*$
set. Indeed, if D does not have uniform density one, then there exists a Følner sequence
![]() $(F_k)_{k\in {\mathbb {N}}}$
in
$(F_k)_{k\in {\mathbb {N}}}$
in
![]() $G^d$
for which
$G^d$
for which
![]() $\overline d_{(F_k)}(D)<1$
. Let
$\overline d_{(F_k)}(D)<1$
. Let
![]() $E=G^d\setminus D$
and note that
$E=G^d\setminus D$
and note that
![]() $\overline d_{(F_k)}(E)>0$
. By Proposition 5.8, E contains a
$\overline d_{(F_k)}(E)>0$
. By Proposition 5.8, E contains a
![]() $\tilde {\Sigma }_m$
set. This implies that D is not a
$\tilde {\Sigma }_m$
set. This implies that D is not a
![]() $\tilde {\Sigma }_m^*$
.
$\tilde {\Sigma }_m^*$
.
5.3 The ubiquity of
 $\tilde {\Sigma }_m^*$
sets
$\tilde {\Sigma }_m^*$
sets
In this subsection we will show that there exists a broad class of subgroups of
![]() $G^d$
with the property that, for each group H from this class, any
$G^d$
with the property that, for each group H from this class, any
![]() $\tilde {\Sigma }_m^*$
set in
$\tilde {\Sigma }_m^*$
set in
![]() $G^d$
has a large intersection with H. In fact, we will show that either a subgroup H belongs to this class or
$G^d$
has a large intersection with H. In fact, we will show that either a subgroup H belongs to this class or
![]() $G^d\setminus H$
is a
$G^d\setminus H$
is a
![]() $\tilde {\Sigma }_m^*$
set for any
$\tilde {\Sigma }_m^*$
set for any
![]() $m\in {\mathbb {N}}$
.
$m\in {\mathbb {N}}$
.
Definition 5.10. Let
![]() $(G,+)$
be a countable abelian group, let
$(G,+)$
be a countable abelian group, let
![]() $d\in {\mathbb {N}}$
and let H be a subgroup of
$d\in {\mathbb {N}}$
and let H be a subgroup of
![]() $G^d$
. We say that H is an admissible subgroup of
$G^d$
. We say that H is an admissible subgroup of
![]() $G^d$
if there exist non-degenerated and essentially distinct sequences
$G^d$
if there exist non-degenerated and essentially distinct sequences
![]() $(g_k^{(1)})_{k\in {\mathbb {N}}},\ldots,$
$(g_k^{(1)})_{k\in {\mathbb {N}}},\ldots,$
![]() $(g_k^{(d)})_{k\in {\mathbb {N}}}$
in G such that
$(g_k^{(d)})_{k\in {\mathbb {N}}}$
in G such that
Example 5.11. Let
![]() $(G,+)$
be a countable abelian group and let
$(G,+)$
be a countable abelian group and let
![]() $H=\{(g,h,0)\,|\,g, h\in G\}\subseteq G^3$
. Clearly, H is not an admissible subgroup of
$H=\{(g,h,0)\,|\,g, h\in G\}\subseteq G^3$
. Clearly, H is not an admissible subgroup of
![]() $G^3$
.
$G^3$
.
Example 5.12. Let
![]() $(G,+)$
be a countable abelian group with an element g of infinite order. For any
$(G,+)$
be a countable abelian group with an element g of infinite order. For any
![]() $d\in {\mathbb {N}}$
and any distinct
$d\in {\mathbb {N}}$
and any distinct
![]() $a_1,\ldots ,a_d\in {\mathbb {Z}}\setminus \{0\}$
, the set
$a_1,\ldots ,a_d\in {\mathbb {Z}}\setminus \{0\}$
, the set
![]() $\{(ka_1 g,ka_2 g,\ldots ,ka_dg)\,|\, k\in {\mathbb {Z}}\}$
is an admissible subgroup of
$\{(ka_1 g,ka_2 g,\ldots ,ka_dg)\,|\, k\in {\mathbb {Z}}\}$
is an admissible subgroup of
![]() $G^d$
.
$G^d$
.
Example 5.13. Let
![]() $(G,+)$
be a countable abelian torsion group (that is, each of its elements has finite order). There exist a sequence
$(G,+)$
be a countable abelian torsion group (that is, each of its elements has finite order). There exist a sequence
![]() $(g_k)_{k\in {\mathbb {N}}}$
in G and a nested sequence of finite subgroups
$(g_k)_{k\in {\mathbb {N}}}$
in G and a nested sequence of finite subgroups
![]() $(G_N)_{N\in {\mathbb {N}}}$
with the following properties: (i)
$(G_N)_{N\in {\mathbb {N}}}$
with the following properties: (i)
![]() $G_N$
is generated by
$G_N$
is generated by
![]() $\{g_1,\ldots ,g_N\}$
; (ii) for each
$\{g_1,\ldots ,g_N\}$
; (ii) for each
![]() $k\in {\mathbb {N}}$
,
$k\in {\mathbb {N}}$
,
![]() $g_{k+1}\not \in G_k$
. Then, for any
$g_{k+1}\not \in G_k$
. Then, for any
![]() $d\in {\mathbb {N}}$
and any distinct
$d\in {\mathbb {N}}$
and any distinct
![]() $a_1,\ldots ,a_d\in {\mathbb {N}}$
, the group generated by the set
$a_1,\ldots ,a_d\in {\mathbb {N}}$
, the group generated by the set
![]() $\{(g_{a_1k},g_{a_2k},\ldots ,g_{a_dk})\,|\, k\in {\mathbb {N}}\}$
is an admissible subgroup of
$\{(g_{a_1k},g_{a_2k},\ldots ,g_{a_dk})\,|\, k\in {\mathbb {N}}\}$
is an admissible subgroup of
![]() $G^d$
. Indeed, note that, for any
$G^d$
. Indeed, note that, for any
![]() $k\in {\mathbb {N}}$
and any
$k\in {\mathbb {N}}$
and any
![]() $a,b\in {\mathbb {N}}$
with
$a,b\in {\mathbb {N}}$
with
![]() $a<b$
,
$a<b$
,
![]() $g_{ak}\not \in G_{ak-1}$
and
$g_{ak}\not \in G_{ak-1}$
and
![]() $(g_{bk}-g_{ak})\not \in G_{ak}$
. So
$(g_{bk}-g_{ak})\not \in G_{ak}$
. So
![]() $\lim _{k\rightarrow \infty }g_{ak}=\infty $
and
$\lim _{k\rightarrow \infty }g_{ak}=\infty $
and
![]() $\lim _{k\rightarrow \infty }(g_{bk}-g_{ak})=\infty $
.
$\lim _{k\rightarrow \infty }(g_{bk}-g_{ak})=\infty $
.
The following proposition provides a useful characterization of admissible subgroups.
Proposition 5.14. Let
![]() $(G,+)$
be a countable abelian group, let
$(G,+)$
be a countable abelian group, let
![]() $d\in {\mathbb {N}}$
and let H be a subgroup of
$d\in {\mathbb {N}}$
and let H be a subgroup of
![]() $G^d$
. The following statements are equivalent.
$G^d$
. The following statements are equivalent.
-
(i) H is an admissible subgroup of
 $G^d$
.
$G^d$
. -
(ii) There exist an
 $m\in {\mathbb {N}}$
and a
$m\in {\mathbb {N}}$
and a
 $\tilde {\Sigma }_m$
set
$\tilde {\Sigma }_m$
set
 $E\subseteq G^d$
such that
$E\subseteq G^d$
such that
 $E\subseteq H$
.
$E\subseteq H$
. -
(iii) For any
 $m\in {\mathbb {N}}$
, there exists a
$m\in {\mathbb {N}}$
, there exists a
 $\tilde {\Sigma }_m$
set
$\tilde {\Sigma }_m$
set
 $E\subseteq G^d$
such that
$E\subseteq G^d$
such that
 $E\subseteq H$
.
$E\subseteq H$
. -
(iv) There exists an
 $\tilde {\text {IP}}$
set
$\tilde {\text {IP}}$
set
 $E\subseteq G^d$
such that
$E\subseteq G^d$
such that
 $E\subseteq H$
.
$E\subseteq H$
. -
(v) For any
 $j\in \{1,\ldots ,d\}$
,
$j\in \{1,\ldots ,d\}$
,
 $\pi _j(H)$
is infinite and, for any
$\pi _j(H)$
is infinite and, for any
 $i\neq j$
,
$i\neq j$
,
 $(\pi _j-\pi _i)(H)$
is also infinite, where for each
$(\pi _j-\pi _i)(H)$
is also infinite, where for each
 $j\in \{1,\ldots ,d\}$
,
$j\in \{1,\ldots ,d\}$
,
 $\pi _j:H\rightarrow G$
is defined by
$\pi _j:H\rightarrow G$
is defined by
 $\pi _j(g_1,\ldots ,g_d)=g_j$
.
$\pi _j(g_1,\ldots ,g_d)=g_j$
.
Proof. It is not hard to see that (i) and (ii) are equivalent. The implications (i)
![]() $\implies $
(iii), (iii)
$\implies $
(iii), (iii)
![]() $\implies $
(iv) and (iv)
$\implies $
(iv) and (iv)
![]() $\implies $
(v) are trivial. We will now prove (v)
$\implies $
(v) are trivial. We will now prove (v)
![]() $\implies $
(i).
$\implies $
(i).
Let
![]() $P=\{\pi _j\,|\,j\in \{1,\ldots ,d\}\}\cup \{\pi _j-\pi _i\,|\,i,j\in \{1,\ldots ,d\},\,i\neq j\}$
and let M be the largest non-negative integer for which there exist an
$P=\{\pi _j\,|\,j\in \{1,\ldots ,d\}\}\cup \{\pi _j-\pi _i\,|\,i,j\in \{1,\ldots ,d\},\,i\neq j\}$
and let M be the largest non-negative integer for which there exist an
![]() $F\subseteq P$
with
$F\subseteq P$
with
![]() $|F|=M$
and a sequence
$|F|=M$
and a sequence
![]() $(\textbf g_k)_{k\in {\mathbb {N}}}$
in H such that, for any
$(\textbf g_k)_{k\in {\mathbb {N}}}$
in H such that, for any
![]() $\pi \in F$
,
$\pi \in F$
,
![]() $\lim _{k\rightarrow \infty }\pi (\textbf g_k)=\infty $
. Since
$\lim _{k\rightarrow \infty }\pi (\textbf g_k)=\infty $
. Since
![]() $|P|=d^2$
, we have
$|P|=d^2$
, we have
![]() $M\leq d^2$
. Also, since, for each
$M\leq d^2$
. Also, since, for each
![]() $\pi \in P$
,
$\pi \in P$
,
![]() $\pi (H)$
is infinite,
$\pi (H)$
is infinite,
![]() $M\geq 1$
. If
$M\geq 1$
. If
![]() $M=d^2$
, then (i) holds. So, assume for contradiction that
$M=d^2$
, then (i) holds. So, assume for contradiction that
![]() $M<d^2$
.
$M<d^2$
.
By the definition of M, there exist a set
![]() $F_0\subseteq P$
with
$F_0\subseteq P$
with
![]() $|F_0|=M$
and a sequence
$|F_0|=M$
and a sequence
![]() $(\textbf g_k)_{k\in {\mathbb {N}}}$
in H such that if
$(\textbf g_k)_{k\in {\mathbb {N}}}$
in H such that if
![]() $\pi \in F_0$
,
$\pi \in F_0$
,
![]() $\lim _{k\rightarrow \infty }\pi (\textbf g_k)=\infty $
and if
$\lim _{k\rightarrow \infty }\pi (\textbf g_k)=\infty $
and if
![]() $\pi \in (P\setminus F_0)$
, then there exists a finite set
$\pi \in (P\setminus F_0)$
, then there exists a finite set
![]() $A_{\pi }\subseteq G$
such that
$A_{\pi }\subseteq G$
such that
![]() $\{\pi (\textbf g_k)\,|\,k\in {\mathbb {N}}\}\subseteq A_{\pi }$
. By passing, if needed, to a subsequence, we can assume that, for each
$\{\pi (\textbf g_k)\,|\,k\in {\mathbb {N}}\}\subseteq A_{\pi }$
. By passing, if needed, to a subsequence, we can assume that, for each
![]() $\pi \in (P\setminus F_0)$
, there exists a
$\pi \in (P\setminus F_0)$
, there exists a
![]() $g_{\pi }\in G$
such that
$g_{\pi }\in G$
such that
![]() $\lim _{k\rightarrow \infty }\pi (\textbf g_k)=g_{\pi }$
. Let
$\lim _{k\rightarrow \infty }\pi (\textbf g_k)=g_{\pi }$
. Let
![]() $\pi _0\in (P\setminus F_0)$
. By (v), there exists a sequence
$\pi _0\in (P\setminus F_0)$
. By (v), there exists a sequence
![]() $(\textbf g^{\prime }_k)_{k\in {\mathbb {N}}}$
in H such that
$(\textbf g^{\prime }_k)_{k\in {\mathbb {N}}}$
in H such that
![]() $\lim _{k\rightarrow \infty }\pi _0(\textbf g^{\prime }_k)=\infty $
. Note that, for any finite set
$\lim _{k\rightarrow \infty }\pi _0(\textbf g^{\prime }_k)=\infty $
. Note that, for any finite set
![]() $A\subseteq H$
, any
$A\subseteq H$
, any
![]() $\pi \in F_0$
and any
$\pi \in F_0$
and any
![]() $t\in {\mathbb {N}}$
, there exists a
$t\in {\mathbb {N}}$
, there exists a
![]() $k\in {\mathbb {N}}$
such that, for any
$k\in {\mathbb {N}}$
such that, for any
![]() $k'>k$
,
$k'>k$
,
Also, note that there exists a
![]() $k_0\in {\mathbb {N}}$
such that, for any
$k_0\in {\mathbb {N}}$
such that, for any
![]() $k>k_0$
,
$k>k_0$
,
![]() $\pi _0(\textbf g_k)=g_{\pi _0}$
. It follows that we can find an increasing sequence
$\pi _0(\textbf g_k)=g_{\pi _0}$
. It follows that we can find an increasing sequence
![]() $(k_t)_{t\in {\mathbb {N}}}$
in
$(k_t)_{t\in {\mathbb {N}}}$
in
![]() ${\mathbb {N}}$
for which
${\mathbb {N}}$
for which
![]() $\lim _{t\rightarrow \infty }\pi (\textbf g_{k_t}+\textbf g^{\prime }_t)=\infty $
for each
$\lim _{t\rightarrow \infty }\pi (\textbf g_{k_t}+\textbf g^{\prime }_t)=\infty $
for each
![]() $\pi \in F_0\cup \{\pi _0\}$
. This contradicts the definition of M, completing the proof.
$\pi \in F_0\cup \{\pi _0\}$
. This contradicts the definition of M, completing the proof.
Corollary 5.15. Let
![]() $(G,+)$
be a countable abelian group and let
$(G,+)$
be a countable abelian group and let
![]() $d\in {\mathbb {N}}$
. A subgroup H of
$d\in {\mathbb {N}}$
. A subgroup H of
![]() $G^d$
is either admissible or, for any
$G^d$
is either admissible or, for any
![]() $m\in {\mathbb {N}}$
,
$m\in {\mathbb {N}}$
,
![]() $G^d\setminus H$
is a
$G^d\setminus H$
is a
![]() $\tilde {\Sigma }_m^*$
set.
$\tilde {\Sigma }_m^*$
set.
Proof. If H is not an admissible subgroup, Proposition 5.14(ii) implies that, for each
![]() $m\in {\mathbb {N}}$
, H does not contain any
$m\in {\mathbb {N}}$
, H does not contain any
![]() $\tilde {\Sigma }_m$
set in
$\tilde {\Sigma }_m$
set in
![]() $G^d$
. Thus,
$G^d$
. Thus,
![]() $G^d\setminus H$
is a
$G^d\setminus H$
is a
![]() $\tilde {\Sigma }_m^*$
set for each
$\tilde {\Sigma }_m^*$
set for each
![]() $m\in {\mathbb {N}}$
.
$m\in {\mathbb {N}}$
.
Before stating and proving one of the main results of this subsection which deals with the ubiquity of
![]() $\tilde {\Sigma }_m^*$
sets in admissible subgroups (Theorem 5.20 below), we need one more definition and a technical lemma.
$\tilde {\Sigma }_m^*$
sets in admissible subgroups (Theorem 5.20 below), we need one more definition and a technical lemma.
Definition 5.16. Let
![]() $(G,+)$
be a countable abelian group, let
$(G,+)$
be a countable abelian group, let
![]() $d,m\in {\mathbb {N}}$
and let
$d,m\in {\mathbb {N}}$
and let
![]() $H\subseteq G^d$
be an admissible subgroup. A set
$H\subseteq G^d$
be an admissible subgroup. A set
![]() $E\subseteq H$
is called an H-
$E\subseteq H$
is called an H-
![]() $\tilde {\Sigma }_m^*$
set if it has a non-trivial intersection with every
$\tilde {\Sigma }_m^*$
set if it has a non-trivial intersection with every
![]() $\tilde {\Sigma }_m$
set contained in H. Similarly, a set
$\tilde {\Sigma }_m$
set contained in H. Similarly, a set
![]() $E\subseteq H$
is called an H-
$E\subseteq H$
is called an H-
![]() $\tilde {\text {IP}}^{\mathrm {*}}$
set if it has a non-trivial intersection with every
$\tilde {\text {IP}}^{\mathrm {*}}$
set if it has a non-trivial intersection with every
![]() $\tilde {\text {IP}}$
set contained in H.
$\tilde {\text {IP}}$
set contained in H.
Remark 5.17. Let
![]() $(G,+)$
be a countable abelian group, let
$(G,+)$
be a countable abelian group, let
![]() $d\in {\mathbb {N}}$
and let
$d\in {\mathbb {N}}$
and let
![]() $H\subseteq G^d$
be an admissible subgroup of
$H\subseteq G^d$
be an admissible subgroup of
![]() $G^d$
. It is useful to perceive H-
$G^d$
. It is useful to perceive H-
![]() $\tilde {\Sigma }_m^*$
sets as relative versions of
$\tilde {\Sigma }_m^*$
sets as relative versions of
![]() $\tilde {\Sigma }_m^*$
sets in
$\tilde {\Sigma }_m^*$
sets in
![]() $G^d$
. Note that if H is a proper subgroup of
$G^d$
. Note that if H is a proper subgroup of
![]() $G^d$
, H-
$G^d$
, H-
![]() $\tilde {\Sigma }_m^*$
sets are not
$\tilde {\Sigma }_m^*$
sets are not
![]() $\tilde {\Sigma }_m^*$
. Indeed, since, for each
$\tilde {\Sigma }_m^*$
. Indeed, since, for each
![]() $m\in {\mathbb {N}}$
, any translation of a
$m\in {\mathbb {N}}$
, any translation of a
![]() $\tilde {\Sigma }_m$
set in
$\tilde {\Sigma }_m$
set in
![]() $G^d$
is again a
$G^d$
is again a
![]() $\tilde {\Sigma }_m$
set, every coset of H contains a
$\tilde {\Sigma }_m$
set, every coset of H contains a
![]() $\tilde {\Sigma }_m$
set in
$\tilde {\Sigma }_m$
set in
![]() $G^d$
. It follows that
$G^d$
. It follows that
![]() $G^d\setminus H$
contains a
$G^d\setminus H$
contains a
![]() $\tilde {\Sigma }_m$
set for each
$\tilde {\Sigma }_m$
set for each
![]() $m\in {\mathbb {N}}$
. Hence, no H-
$m\in {\mathbb {N}}$
. Hence, no H-
![]() $\tilde {\Sigma }_m^*$
set is a
$\tilde {\Sigma }_m^*$
set is a
![]() $\tilde {\Sigma }_m^*$
set.
$\tilde {\Sigma }_m^*$
set.
Remark 5.18. Let
![]() $(G,+)$
be a countable abelian group, let
$(G,+)$
be a countable abelian group, let
![]() $d,m\in {\mathbb {N}}$
, let
$d,m\in {\mathbb {N}}$
, let
![]() $H\subseteq G^d$
be an admissible subgroup and let E be a
$H\subseteq G^d$
be an admissible subgroup and let E be a
![]() $\tilde {\Sigma }_m^*$
set in
$\tilde {\Sigma }_m^*$
set in
![]() $G^d$
. It follows from the definition that
$G^d$
. It follows from the definition that
![]() $E\cap H$
is a H-
$E\cap H$
is a H-
![]() $\tilde {\Sigma }_m^*$
set. Indeed, let
$\tilde {\Sigma }_m^*$
set. Indeed, let
![]() $D\subseteq H$
be a
$D\subseteq H$
be a
![]() $\tilde {\Sigma }_m$
set. We have
$\tilde {\Sigma }_m$
set. We have
![]() $(E\cap H)\cap D=E\cap D\neq \emptyset $
. Note also that, for any
$(E\cap H)\cap D=E\cap D\neq \emptyset $
. Note also that, for any
![]() $\textbf g\in G^d$
,
$\textbf g\in G^d$
,
![]() $E\cap (\textbf g+H)$
is the translation of the H-
$E\cap (\textbf g+H)$
is the translation of the H-
![]() $\tilde {\Sigma }_m^*$
set
$\tilde {\Sigma }_m^*$
set
![]() $(-\textbf g+E)\cap H$
. Thus, the cosets of H have a large intersection with E as well.
$(-\textbf g+E)\cap H$
. Thus, the cosets of H have a large intersection with E as well.
Lemma 5.19. Let
![]() $(G,+)$
be a countable abelian group, let
$(G,+)$
be a countable abelian group, let
![]() $d,m\in {\mathbb {N}}$
, let H be an admissible subgroup of
$d,m\in {\mathbb {N}}$
, let H be an admissible subgroup of
![]() $G^d$
and let
$G^d$
and let
![]() $(F_k)_{k\in {\mathbb {N}}}$
be a Følner sequence in H. Any
$(F_k)_{k\in {\mathbb {N}}}$
be a Følner sequence in H. Any
![]() $E\subseteq H$
with
$E\subseteq H$
with
![]() $\overline d_{(F_k)}(E)>0$
contains a
$\overline d_{(F_k)}(E)>0$
contains a
![]() $\tilde {\Sigma }_m$
set.
$\tilde {\Sigma }_m$
set.
Proof. Since H is admissible, there exists an
![]() $\tilde {\text {IP}}$
set
$\tilde {\text {IP}}$
set
![]() $D'\subseteq H$
. The result in question follows by replacing D by
$D'\subseteq H$
. The result in question follows by replacing D by
![]() $D'$
in the proof of Proposition 5.8 and applying an adequate modification of Proposition 5.7.
$D'$
in the proof of Proposition 5.8 and applying an adequate modification of Proposition 5.7.
Theorem 5.20. Let
![]() $(G,+)$
be a countable abelian group, let
$(G,+)$
be a countable abelian group, let
![]() $d,m\in {\mathbb {N}}$
and let
$d,m\in {\mathbb {N}}$
and let
![]() $H\subseteq G^d$
be an admissible subgroup. Any H-
$H\subseteq G^d$
be an admissible subgroup. Any H-
![]() $\tilde {\Sigma }_m^*$
set is an H-
$\tilde {\Sigma }_m^*$
set is an H-
![]() $\tilde {\text {IP}}^{\mathrm {*}}$
set and has uniform density one in H.
$\tilde {\text {IP}}^{\mathrm {*}}$
set and has uniform density one in H.
Proof. Let
![]() $E'\subseteq H$
be an H-
$E'\subseteq H$
be an H-
![]() $\tilde {\Sigma }_m^*$
set. By Lemma 5.3, every
$\tilde {\Sigma }_m^*$
set. By Lemma 5.3, every
![]() $\tilde {\text {IP}}$
set contains a
$\tilde {\text {IP}}$
set contains a
![]() $\tilde {\Sigma }_m$
set. It follows that
$\tilde {\Sigma }_m$
set. It follows that
![]() $E'$
is an H-
$E'$
is an H-
![]() $\tilde {\text {IP}}^{\mathrm {*}}$
set. By Lemma 5.19, we can argue as in the proof of Corollary 5.9 to show that
$\tilde {\text {IP}}^{\mathrm {*}}$
set. By Lemma 5.19, we can argue as in the proof of Corollary 5.9 to show that
![]() $E'$
has uniform density one in H.
$E'$
has uniform density one in H.
Corollary 5.21. Let
![]() $(G,+)$
be a countable abelian group, let
$(G,+)$
be a countable abelian group, let
![]() $d\in {\mathbb {N}}$
, let H be an admissible subgroup of
$d\in {\mathbb {N}}$
, let H be an admissible subgroup of
![]() $G^d$
and let
$G^d$
and let
![]() $(X,\mathcal A,\mu ,(T_g)_{g\in G})$
be a strongly mixing system. For any
$(X,\mathcal A,\mu ,(T_g)_{g\in G})$
be a strongly mixing system. For any
![]() $\textbf g\in G^d$
, each set of the form
$\textbf g\in G^d$
, each set of the form
![]() $R_{\epsilon }(A_0,\ldots ,A_{\ell })\cap (\textbf g+ H)$
is the translation of a set with uniform density one in H.
$R_{\epsilon }(A_0,\ldots ,A_{\ell })\cap (\textbf g+ H)$
is the translation of a set with uniform density one in H.
A natural class of admissible subgroups in
![]() $G^d$
is provided by the one-parameter subgroups of the form
$G^d$
is provided by the one-parameter subgroups of the form
where
![]() $\phi _1,\ldots ,\phi _d:G\rightarrow G$
are homomorphisms such that, for any
$\phi _1,\ldots ,\phi _d:G\rightarrow G$
are homomorphisms such that, for any
![]() $j\in \{1,\ldots ,d\}$
,
$j\in \{1,\ldots ,d\}$
,
![]() $|\!\ker (\phi _j)|<\infty $
and, for any
$|\!\ker (\phi _j)|<\infty $
and, for any
![]() $i\neq j$
,
$i\neq j$
,
![]() $|\ker (\phi _j-\phi _i)|<\infty $
. The following proposition, alluded to in Remark 4.5, involves preimages of sets in
$|\ker (\phi _j-\phi _i)|<\infty $
. The following proposition, alluded to in Remark 4.5, involves preimages of sets in
![]() $G^d$
via the elements of
$G^d$
via the elements of
![]() $H_{\phi _1,\ldots ,\phi _d}$
and provides an alternative proof of Theorem 4.4.
$H_{\phi _1,\ldots ,\phi _d}$
and provides an alternative proof of Theorem 4.4.
Proposition 5.22. Let
![]() $(G,+)$
be a countable abelian group, let
$(G,+)$
be a countable abelian group, let
![]() $d,m\in {\mathbb {N}}$
and let
$d,m\in {\mathbb {N}}$
and let
![]() $\phi _1,\ldots ,\phi _d:G\rightarrow G$
be homomorphisms such that, for any
$\phi _1,\ldots ,\phi _d:G\rightarrow G$
be homomorphisms such that, for any
![]() $j\in \{1,\ldots ,d\}$
,
$j\in \{1,\ldots ,d\}$
,
![]() $\ker (\phi _j)$
is finite and, for any
$\ker (\phi _j)$
is finite and, for any
![]() $i\neq j$
,
$i\neq j$
,
![]() $\ker (\phi _j-\phi _i)$
is also finite. If
$\ker (\phi _j-\phi _i)$
is also finite. If
![]() $E\subseteq G^d$
is a
$E\subseteq G^d$
is a
![]() $\tilde {\Sigma }_m^*$
set, then
$\tilde {\Sigma }_m^*$
set, then
![]() $E'=\{g\in G\,|\,(\phi _1(g),\ldots ,\phi _d(g))\in E\}$
is a
$E'=\{g\in G\,|\,(\phi _1(g),\ldots ,\phi _d(g))\in E\}$
is a
![]() $\Sigma _m^*$
set in G.
$\Sigma _m^*$
set in G.
Proof. Let
![]() $D\subseteq G$
be the
$D\subseteq G$
be the
![]() $\Sigma _m$
set in G generated by the non-degenerated sequence
$\Sigma _m$
set in G generated by the non-degenerated sequence
![]() $(\textbf g_k)_{k\in {\mathbb {N}}}=(g_{k,1},\ldots ,g_{k,m})_{k\in {\mathbb {N}}}$
in
$(\textbf g_k)_{k\in {\mathbb {N}}}=(g_{k,1},\ldots ,g_{k,m})_{k\in {\mathbb {N}}}$
in
![]() $G^m$
(that is,
$G^m$
(that is,
![]() $D=\{g_{\alpha }\,|\,\alpha \in {\mathbb {N}}^{(m)}\}$
). We will show that
$D=\{g_{\alpha }\,|\,\alpha \in {\mathbb {N}}^{(m)}\}$
). We will show that
![]() $D\cap E'\neq \emptyset $
.
$D\cap E'\neq \emptyset $
.
By our assumption on
![]() $\phi _1,\ldots ,\phi _d$
, for each
$\phi _1,\ldots ,\phi _d$
, for each
![]() $j\in \{1,\ldots ,m\}$
, the sequences
$j\in \{1,\ldots ,m\}$
, the sequences
![]() $(\phi _1(g_{k,j}))_{k\in {\mathbb {N}}},\ldots ,(\phi _d(g_{k,j}))_{k\in {\mathbb {N}}}$
are non-degenerated and essentially distinct. Thus, the set
$(\phi _1(g_{k,j}))_{k\in {\mathbb {N}}},\ldots ,(\phi _d(g_{k,j}))_{k\in {\mathbb {N}}}$
are non-degenerated and essentially distinct. Thus, the set
![]() $D'=\{(\phi _1(g_{\alpha }),\ldots ,\phi _d(g_{\alpha }))\,|\,\alpha \in {\mathbb {N}}^{(m)}\}$
is a
$D'=\{(\phi _1(g_{\alpha }),\ldots ,\phi _d(g_{\alpha }))\,|\,\alpha \in {\mathbb {N}}^{(m)}\}$
is a
![]() $\tilde {\Sigma }_m$
set in
$\tilde {\Sigma }_m$
set in
![]() $G^d$
. Noting that
$G^d$
. Noting that
![]() $D'\cap E\neq \emptyset $
, we obtain
$D'\cap E\neq \emptyset $
, we obtain
![]() $D\cap E'\neq \emptyset $
.
$D\cap E'\neq \emptyset $
.
So far we have been focusing on the massivity and ubiquity of general
![]() $\tilde {\Sigma }_{\ell }^*$
sets. However the ‘dynamical’
$\tilde {\Sigma }_{\ell }^*$
sets. However the ‘dynamical’
![]() $\tilde {\Sigma }_{\ell }^*$
sets
$\tilde {\Sigma }_{\ell }^*$
sets
![]() $R_{\epsilon }(A_0,\ldots ,A_{\ell })$
, are even more prevalent in
$R_{\epsilon }(A_0,\ldots ,A_{\ell })$
, are even more prevalent in
![]() $G^{\ell }$
. For example, assuming for convenience that
$G^{\ell }$
. For example, assuming for convenience that
![]() $G={\mathbb {Z}}$
, one can show that the sets of the form
$G={\mathbb {Z}}$
, one can show that the sets of the form
![]() $R_{\epsilon }(A_0,\ldots ,A_{\ell })$
have an ample presence in ‘polynomial’ subsets of
$R_{\epsilon }(A_0,\ldots ,A_{\ell })$
have an ample presence in ‘polynomial’ subsets of
![]() ${\mathbb {Z}}^{\ell }$
. This is illustrated by the following polynomial extension of Proposition 4.1 (which is proved in a companion paper [Reference Bergelson and Zelada9]).
${\mathbb {Z}}^{\ell }$
. This is illustrated by the following polynomial extension of Proposition 4.1 (which is proved in a companion paper [Reference Bergelson and Zelada9]).
Theorem 5.23. Let
![]() $\ell \in {\mathbb {N}}$
and let
$\ell \in {\mathbb {N}}$
and let
![]() $p_1,\ldots ,p_{\ell }\in {\mathbb {Z}}[x]$
be non-constant polynomials such that, for any distinct
$p_1,\ldots ,p_{\ell }\in {\mathbb {Z}}[x]$
be non-constant polynomials such that, for any distinct
![]() $i,j\in \{1,\ldots ,\ell \}$
,
$i,j\in \{1,\ldots ,\ell \}$
,
![]() $\deg (p_j-p_i)>0$
. There exists an
$\deg (p_j-p_i)>0$
. There exists an
![]() $m\in {\mathbb {N}}$
such that, for any strongly mixing system
$m\in {\mathbb {N}}$
such that, for any strongly mixing system
![]() $(X,\mathcal A,\mu , T)$
, any
$(X,\mathcal A,\mu , T)$
, any
![]() $\epsilon>0$
and any
$\epsilon>0$
and any
![]() $A_0,\ldots ,A_{\ell }\in \mathcal A$
, the set
$A_0,\ldots ,A_{\ell }\in \mathcal A$
, the set
 $$ \begin{align} R_{\epsilon}^{p_1,\ldots,p_{\ell}}(A_0,\ldots,A_{\ell})=\bigg\{{\kern-1pt}n\in{\mathbb{Z}}\,\bigg|\,\,\bigg|\mu(A_0\cap T^{p_1(n)}A_1\cap\cdots\cap T^{p_{\ell}(n)}A_{\ell})-{\kern-1pt}\prod_{j=0}^{\ell}\mu(A_j)\bigg|{\kern-1pt}<{\kern-1pt}\epsilon{\kern-1pt}\bigg\} \end{align} $$
$$ \begin{align} R_{\epsilon}^{p_1,\ldots,p_{\ell}}(A_0,\ldots,A_{\ell})=\bigg\{{\kern-1pt}n\in{\mathbb{Z}}\,\bigg|\,\,\bigg|\mu(A_0\cap T^{p_1(n)}A_1\cap\cdots\cap T^{p_{\ell}(n)}A_{\ell})-{\kern-1pt}\prod_{j=0}^{\ell}\mu(A_j)\bigg|{\kern-1pt}<{\kern-1pt}\epsilon{\kern-1pt}\bigg\} \end{align} $$
is
![]() $\Sigma _m^*$
.
$\Sigma _m^*$
.
The following proposition shows that, in general,
![]() $\tilde {\Sigma }_{\ell }^*$
sets, unlike the sets of the form
$\tilde {\Sigma }_{\ell }^*$
sets, unlike the sets of the form
![]() $R_{\epsilon }(A_0,\ldots ,A_{\ell })$
, can be disjoint from the polynomial sets
$R_{\epsilon }(A_0,\ldots ,A_{\ell })$
, can be disjoint from the polynomial sets
![]() $H_{p_1,\ldots ,p_{\ell }}=\{(p_1(n),\ldots ,p_{\ell }(n))\,|\,n\in {\mathbb {Z}}\}$
, where
$H_{p_1,\ldots ,p_{\ell }}=\{(p_1(n),\ldots ,p_{\ell }(n))\,|\,n\in {\mathbb {Z}}\}$
, where
![]() $p_1,\ldots ,p_{\ell }\in {\mathbb {Z}}[x]$
.
$p_1,\ldots ,p_{\ell }\in {\mathbb {Z}}[x]$
.
Proposition 5.24. Let
![]() $\ell \in {\mathbb {N}}$
and let
$\ell \in {\mathbb {N}}$
and let
![]() $p_1,\ldots ,p_{\ell }\in {\mathbb {Z}}[x]$
be non-constant polynomials such that, for any distinct
$p_1,\ldots ,p_{\ell }\in {\mathbb {Z}}[x]$
be non-constant polynomials such that, for any distinct
![]() $i,j\in \{1,\ldots ,\ell \}$
,
$i,j\in \{1,\ldots ,\ell \}$
,
![]() $\deg (p_j-p_i)>0$
. Suppose that
$\deg (p_j-p_i)>0$
. Suppose that
![]() $\deg (p_1)>1$
. Then, for any
$\deg (p_1)>1$
. Then, for any
![]() $m\geq 2$
,
$m\geq 2$
,
![]() $H_{p_1,\ldots ,p_{\ell }}$
contains no
$H_{p_1,\ldots ,p_{\ell }}$
contains no
![]() $\tilde {\Sigma }_m$
sets. Equivalently,
$\tilde {\Sigma }_m$
sets. Equivalently,
![]() ${\mathbb {Z}}^{\ell }\setminus H_{p_1,\ldots ,p_{\ell }}$
is a
${\mathbb {Z}}^{\ell }\setminus H_{p_1,\ldots ,p_{\ell }}$
is a
![]() $\tilde {\Sigma }_m^*$
set for each
$\tilde {\Sigma }_m^*$
set for each
![]() $m\geq 2$
.
$m\geq 2$
.
Proof. Since the projection onto the first coordinate of any
![]() $\tilde {\Sigma }_m$
set
$\tilde {\Sigma }_m$
set
![]() $E\subseteq {\mathbb {Z}}^{\ell }$
is a
$E\subseteq {\mathbb {Z}}^{\ell }$
is a
![]() $\Sigma _m$
set in
$\Sigma _m$
set in
![]() ${\mathbb {Z}}$
, it suffices to show that the set
${\mathbb {Z}}$
, it suffices to show that the set
![]() $\{p_1(n)\,|\,n\in {\mathbb {Z}}\}$
contains no
$\{p_1(n)\,|\,n\in {\mathbb {Z}}\}$
contains no
![]() $\Sigma _m$
sets. Suppose for contradiction that
$\Sigma _m$
sets. Suppose for contradiction that
![]() $\{p_1(n)\,|\,n\in {\mathbb {Z}}\}$
contains a
$\{p_1(n)\,|\,n\in {\mathbb {Z}}\}$
contains a
![]() $\Sigma _m$
set
$\Sigma _m$
set
where
![]() $(n_k^{(1)})_{k\in {\mathbb {N}}},\ldots,$
$(n_k^{(1)})_{k\in {\mathbb {N}}},\ldots,$
![]() $(n_k^{(m)})_{k\in {\mathbb {N}}}$
are non-degenerated sequences in
$(n_k^{(m)})_{k\in {\mathbb {N}}}$
are non-degenerated sequences in
![]() ${\mathbb {Z}}$
.
${\mathbb {Z}}$
.
Choose
![]() $t_1,t_2,t_3\in {\mathbb {N}}$
to be such that
$t_1,t_2,t_3\in {\mathbb {N}}$
to be such that
![]() $n^{(1)}_{t_1}<n^{(1)}_{t_2}<n^{(1)}_{t_3}$
and let
$n^{(1)}_{t_1}<n^{(1)}_{t_2}<n^{(1)}_{t_3}$
and let
Clearly, I is an infinite subset of D. So, letting
![]() $a=n_{t_2}^{(1)}-n_{t_1}^{(1)}$
and
$a=n_{t_2}^{(1)}-n_{t_1}^{(1)}$
and
![]() $b=n_{t_3}^{(1)}-n_{t_1}^{(1)}$
, we have
$b=n_{t_3}^{(1)}-n_{t_1}^{(1)}$
, we have
![]() $a+I\subseteq D$
and
$a+I\subseteq D$
and
![]() $b+I\subseteq D$
.
$b+I\subseteq D$
.
Let
![]() $(n_k)_{k\in {\mathbb {N}}}$
be an enumeration of the elements of I. One can find an increasing sequence
$(n_k)_{k\in {\mathbb {N}}}$
be an enumeration of the elements of I. One can find an increasing sequence
![]() $(k_j)_{j\in {\mathbb {N}}}$
for which at least two of the sets
$(k_j)_{j\in {\mathbb {N}}}$
for which at least two of the sets
![]() $\{n_{k_j}\,|\,j\in {\mathbb {N}}\}$
,
$\{n_{k_j}\,|\,j\in {\mathbb {N}}\}$
,
![]() $\{a+n_{k_j}\,|\,j\in {\mathbb {N}}\}$
and
$\{a+n_{k_j}\,|\,j\in {\mathbb {N}}\}$
and
![]() $\{b+n_{k_j}\,|\,j\in {\mathbb {N}}\}$
are contained in at least one of the sets
$\{b+n_{k_j}\,|\,j\in {\mathbb {N}}\}$
are contained in at least one of the sets
![]() $\{p_1(n)\,|\,n\in {\mathbb {N}}\}$
and
$\{p_1(n)\,|\,n\in {\mathbb {N}}\}$
and
![]() $\{p_1(-n)\,|\,n\in {\mathbb {N}}\}$
. We will assume that
$\{p_1(-n)\,|\,n\in {\mathbb {N}}\}$
. We will assume that
![]() $\{a+n_{k_j}\,|\,j\in {\mathbb {N}}\}$
and
$\{a+n_{k_j}\,|\,j\in {\mathbb {N}}\}$
and
![]() $\{b+n_{k_j}\,|\,j\in {\mathbb {N}}\}$
are contained in
$\{b+n_{k_j}\,|\,j\in {\mathbb {N}}\}$
are contained in
![]() $\{p_1(n)\,|\, n\in {\mathbb {N}}\}$
(the other cases can be handled similarly). It follows that there exist infinitely many pairs
$\{p_1(n)\,|\, n\in {\mathbb {N}}\}$
(the other cases can be handled similarly). It follows that there exist infinitely many pairs
![]() $(n,m)\in {\mathbb {N}}\times {\mathbb {N}}$
such that
$(n,m)\in {\mathbb {N}}\times {\mathbb {N}}$
such that
![]() $p_1(n)-p_1(m)=b-a$
. Since
$p_1(n)-p_1(m)=b-a$
. Since
![]() $b>a$
, this contradicts the fact that
$b>a$
, this contradicts the fact that
![]() $\deg (p_1)>1$
.
$\deg (p_1)>1$
.
6 Multiple recurrence for mildly and weakly mixing systems via
 $\mathcal R$
-limits
$\mathcal R$
-limits
As we saw above,
![]() $\mathcal R$
-limits can be successfully used to characterize strong mixing and establish higher-order mixing properties. In this section, we will show that
$\mathcal R$
-limits can be successfully used to characterize strong mixing and establish higher-order mixing properties. In this section, we will show that
![]() $\mathcal R$
-limits can be also useful in dealing with mildly and weakly mixing systems. In particular, we will obtain analogues of Theorem 3.1 for mildly and weakly mixing systems.
$\mathcal R$
-limits can be also useful in dealing with mildly and weakly mixing systems. In particular, we will obtain analogues of Theorem 3.1 for mildly and weakly mixing systems.
6.1 Mildly mixing systems
In this subsection we will deal with mildly mixing systems (see Definition 6.4 below) from the perspective of
![]() $\mathcal R$
-limits. The notion of mild mixing, which lies between weak and strong mixing, was introduced by Walters in 1972 [Reference Walters32] and rediscovered by Furstenberg and Weiss in 1978 [Reference Furstenberg, Weiss, Markley, Martin and Perrizo16]. Mild mixing has multiple equivalent forms (see [Reference Bergelson, Bezuglyi and Kolyada3, Reference Bergelson and Downarowicz4, Reference Furstenberg14, Reference Furstenberg, Weiss, Markley, Martin and Perrizo16]) and plays a fundamental role in IP ergodic theory and its applications, including various refinements of the classical Szemerédi theorem (see [Reference Bergelson and McCutcheon5, Reference Furstenberg and Katznelson15]). The multiple recurrence theorems for mildly mixing systems (see [Reference Bergelson and McCutcheon5, Reference Furstenberg14, Reference Furstenberg and Katznelson15]) utilize the notion of IP-limit which we will presently define. We will then establish a connection between IP-limits and
$\mathcal R$
-limits. The notion of mild mixing, which lies between weak and strong mixing, was introduced by Walters in 1972 [Reference Walters32] and rediscovered by Furstenberg and Weiss in 1978 [Reference Furstenberg, Weiss, Markley, Martin and Perrizo16]. Mild mixing has multiple equivalent forms (see [Reference Bergelson, Bezuglyi and Kolyada3, Reference Bergelson and Downarowicz4, Reference Furstenberg14, Reference Furstenberg, Weiss, Markley, Martin and Perrizo16]) and plays a fundamental role in IP ergodic theory and its applications, including various refinements of the classical Szemerédi theorem (see [Reference Bergelson and McCutcheon5, Reference Furstenberg and Katznelson15]). The multiple recurrence theorems for mildly mixing systems (see [Reference Bergelson and McCutcheon5, Reference Furstenberg14, Reference Furstenberg and Katznelson15]) utilize the notion of IP-limit which we will presently define. We will then establish a connection between IP-limits and
![]() $\mathcal R$
-limits and, finally, prove an analogue of Theorem 3.1 for mildly mixing actions.
$\mathcal R$
-limits and, finally, prove an analogue of Theorem 3.1 for mildly mixing actions.
Definition 6.1. (Cf. [Reference Furstenberg and Katznelson15, Definitions 1.1 and 1.3]) Let
![]() $(X,d)$
be a compact metric space and let
$(X,d)$
be a compact metric space and let
![]() $(x_{\alpha })_{\alpha \in \mathcal F}$
be an
$(x_{\alpha })_{\alpha \in \mathcal F}$
be an
![]() $\mathcal F$
-sequence in X. A set
$\mathcal F$
-sequence in X. A set
![]() $\mathcal F^{(1)}\subseteq \mathcal F$
is an
$\mathcal F^{(1)}\subseteq \mathcal F$
is an
![]() $\mathrm {IP}$
-ring if there exists a sequence
$\mathrm {IP}$
-ring if there exists a sequence
![]() $(\alpha _k)_{k\in {\mathbb {N}}}$
in
$(\alpha _k)_{k\in {\mathbb {N}}}$
in
![]() $\mathcal F$
with
$\mathcal F$
with
![]() $\alpha _k<\alpha _{k+1}$
, for each
$\alpha _k<\alpha _{k+1}$
, for each
![]() $k\in {\mathbb {N}}$
, for which
$k\in {\mathbb {N}}$
, for which
 $$ \begin{align*}\mathcal F^{(1)}=\bigg\{\bigcup_{j\in\alpha}\alpha_j\,\bigg|\,\alpha\in\mathcal F\bigg\}.\end{align*} $$
$$ \begin{align*}\mathcal F^{(1)}=\bigg\{\bigcup_{j\in\alpha}\alpha_j\,\bigg|\,\alpha\in\mathcal F\bigg\}.\end{align*} $$
For any
![]() $\mathrm {IP}$
-ring
$\mathrm {IP}$
-ring
![]() $\mathcal F^{(1)}$
, we write
$\mathcal F^{(1)}$
, we write
if, for every
![]() $\epsilon>0$
, there exists an
$\epsilon>0$
, there exists an
![]() $\alpha _0\in \mathcal F^{(1)}$
such that, for any
$\alpha _0\in \mathcal F^{(1)}$
such that, for any
![]() $\alpha \in \mathcal F^{(1)}$
with
$\alpha \in \mathcal F^{(1)}$
with
![]() $\alpha>\alpha _0$
,
$\alpha>\alpha _0$
,
It follows from a result of Hindman [Reference Hindman17] that if
![]() $(x_{\alpha })_{\alpha \in \mathcal F}$
is an
$(x_{\alpha })_{\alpha \in \mathcal F}$
is an
![]() $\mathcal F$
-sequence in a compact metric space X, then, for any
$\mathcal F$
-sequence in a compact metric space X, then, for any
![]() $\mathrm {IP}$
-ring
$\mathrm {IP}$
-ring
![]() $\mathcal F^{(1)}\subseteq \mathcal F$
, one can always find an
$\mathcal F^{(1)}\subseteq \mathcal F$
, one can always find an
![]() $x\in X$
and an
$x\in X$
and an
![]() $\mathrm {IP}$
-ring
$\mathrm {IP}$
-ring
![]() $\mathcal F^{(2)}\subseteq \mathcal F^{(1)}$
such that
$\mathcal F^{(2)}\subseteq \mathcal F^{(1)}$
such that
(see [Reference Furstenberg14, Theorem 8.14]). In particular, for any countable abelian group
![]() $(G,+)$
, any sequence
$(G,+)$
, any sequence
![]() $(g_k)_{k\in {\mathbb {N}}}$
in G and any probability measure-preserving system
$(g_k)_{k\in {\mathbb {N}}}$
in G and any probability measure-preserving system
![]() $(X,\mathcal A,\mu , (T_g)_{g\in G})$
, there exists an
$(X,\mathcal A,\mu , (T_g)_{g\in G})$
, there exists an
![]() $\mathrm {IP}$
-ring
$\mathrm {IP}$
-ring
![]() $\mathcal F^{(1)}$
for which
$\mathcal F^{(1)}$
for which
exists in the weak operator topology of
![]() $L^2(\mu )$
. This implies (and is equivalent to) the fact that for any
$L^2(\mu )$
. This implies (and is equivalent to) the fact that for any
![]() $A_0,A_1\in \mathcal A$
,
$A_0,A_1\in \mathcal A$
,
exists.
Theorem 6.2. Let
![]() $(X,d)$
be a compact metric space, let
$(X,d)$
be a compact metric space, let
![]() $(G,+)$
be a countable abelian group, let
$(G,+)$
be a countable abelian group, let
![]() $(x_g)_{g\in G}$
be a sequence in X, let
$(x_g)_{g\in G}$
be a sequence in X, let
![]() $x_0\in X$
and let
$x_0\in X$
and let
![]() $(g_k)_{k\in {\mathbb {N}}}$
be a sequence in G. The following statements are equivalent.
$(g_k)_{k\in {\mathbb {N}}}$
be a sequence in G. The following statements are equivalent.
-
(i) For any
 $\mathit {IP}$
-ring
$\mathit {IP}$
-ring
 $\mathcal F^{(1)}\subseteq \mathcal F$
for which
$\mathcal F^{(1)}\subseteq \mathcal F$
for which
 $\mathop {\mathrm {IP}\text {-}\mathrm {lim}}_{\alpha \in \mathcal F^{(1)}}x_{g_{\alpha }}$
exists, one has (6.2)
$\mathop {\mathrm {IP}\text {-}\mathrm {lim}}_{\alpha \in \mathcal F^{(1)}}x_{g_{\alpha }}$
exists, one has (6.2) $$ \begin{align} \mathop{\mathrm{IP}\text{-}\mathrm{lim}}_{\alpha\in\mathcal F^{(1)}}x_{g_{\alpha}}=x_0. \end{align} $$
$$ \begin{align} \mathop{\mathrm{IP}\text{-}\mathrm{lim}}_{\alpha\in\mathcal F^{(1)}}x_{g_{\alpha}}=x_0. \end{align} $$
-
(ii) For any
 $\mathit {IP}$
-ring
$\mathit {IP}$
-ring
 $\mathcal F^{(1)}\subseteq \mathcal F$
, there exist an
$\mathcal F^{(1)}\subseteq \mathcal F$
, there exist an
 $m\in {\mathbb {N}}$
and a sequence
$m\in {\mathbb {N}}$
and a sequence
 $(h_{k,1},\ldots ,h_{k,m})_{k\in {\mathbb {N}}}$
in
$(h_{k,1},\ldots ,h_{k,m})_{k\in {\mathbb {N}}}$
in
 $G^m$
such that
$G^m$
such that
 $\{h_{\alpha }\,|\,\alpha \in {\mathbb {N}}^{(m)}\}\subseteq \{g_{\alpha }\,|\,\alpha \in \mathcal F^{(1)}\}$
and (6.3)
$\{h_{\alpha }\,|\,\alpha \in {\mathbb {N}}^{(m)}\}\subseteq \{g_{\alpha }\,|\,\alpha \in \mathcal F^{(1)}\}$
and (6.3) $$ \begin{align} {\mathop { \mathcal {R}{\text{-}\mathrm{lim}}}_{{\alpha\in{\mathbb{N}}^{(m)}}}}\, x_{h_{\alpha}}=x_0. \end{align} $$
$$ \begin{align} {\mathop { \mathcal {R}{\text{-}\mathrm{lim}}}_{{\alpha\in{\mathbb{N}}^{(m)}}}}\, x_{h_{\alpha}}=x_0. \end{align} $$
Proof. (i)
![]() $\implies $
(ii): Let
$\implies $
(ii): Let
![]() $\mathcal F^{(1)}$
be an
$\mathcal F^{(1)}$
be an
![]() $\mathrm {IP}$
-ring. Since X is compact, we can assume (by passing, if needed, to a sub-
$\mathrm {IP}$
-ring. Since X is compact, we can assume (by passing, if needed, to a sub-
![]() $\mathrm {IP}$
-ring) that
$\mathrm {IP}$
-ring) that
![]() $\mathop {\mathrm {IP}\text {-}\mathrm {lim}}_{\alpha \in \mathcal F^{(1)}}x_{g_{\alpha }}$
exists. Thus, by (i), (6.2) holds. It follows from the definition of an IP-limit that there exists a sequence
$\mathop {\mathrm {IP}\text {-}\mathrm {lim}}_{\alpha \in \mathcal F^{(1)}}x_{g_{\alpha }}$
exists. Thus, by (i), (6.2) holds. It follows from the definition of an IP-limit that there exists a sequence
![]() $(h_k)_{k\in {\mathbb {N}}}$
in G such that
$(h_k)_{k\in {\mathbb {N}}}$
in G such that
![]() $\{h_k\,|\,k\in {\mathbb {N}}\}\subseteq \{g_{\alpha }\,|\,\alpha \in \mathcal F^{(1)}\}$
and
$\{h_k\,|\,k\in {\mathbb {N}}\}\subseteq \{g_{\alpha }\,|\,\alpha \in \mathcal F^{(1)}\}$
and
![]() $\lim _{k\rightarrow \infty }x_{h_k}=x_0$
. This completes the proof of (i)
$\lim _{k\rightarrow \infty }x_{h_k}=x_0$
. This completes the proof of (i)
![]() $\implies $
(ii).
$\implies $
(ii).
(ii)
![]() $\implies $
(i): Let
$\implies $
(i): Let
![]() $\mathcal F^{(1)}$
be an
$\mathcal F^{(1)}$
be an
![]() $\mathrm {IP}$
-ring for which
$\mathrm {IP}$
-ring for which
![]() $\mathop {\mathrm {IP}\text {-}\mathrm {lim}}_{\alpha \in \mathcal F^{(1)}}x_{g_{\alpha }}=y$
for some
$\mathop {\mathrm {IP}\text {-}\mathrm {lim}}_{\alpha \in \mathcal F^{(1)}}x_{g_{\alpha }}=y$
for some
![]() $y\in X$
. Suppose for contradiction that there exists an
$y\in X$
. Suppose for contradiction that there exists an
![]() $\epsilon>0$
for which
$\epsilon>0$
for which
![]() $d(y,x_0)>\epsilon $
. By the definition of an IP-limit, there exists
$d(y,x_0)>\epsilon $
. By the definition of an IP-limit, there exists
![]() $\alpha _0\in \mathcal F$
such that, for any
$\alpha _0\in \mathcal F$
such that, for any
![]() $\alpha \in \mathcal F^{(1)}$
with
$\alpha \in \mathcal F^{(1)}$
with
![]() $\alpha>\alpha _0$
,
$\alpha>\alpha _0$
,
![]() $d(x_{g_{\alpha }},x_0)>\epsilon $
. Since
$d(x_{g_{\alpha }},x_0)>\epsilon $
. Since
![]() $\{\alpha \in \mathcal F^{(1)}\,|\,\alpha>\alpha _0\}$
is an
$\{\alpha \in \mathcal F^{(1)}\,|\,\alpha>\alpha _0\}$
is an
![]() $\mathrm {IP}$
-ring, it follows from (ii) that there exist an
$\mathrm {IP}$
-ring, it follows from (ii) that there exist an
![]() $m\in {\mathbb {N}}$
and a sequence
$m\in {\mathbb {N}}$
and a sequence
![]() $(h_{k,1},\ldots ,h_{k,m})_{k\in {\mathbb {N}}}$
in
$(h_{k,1},\ldots ,h_{k,m})_{k\in {\mathbb {N}}}$
in
![]() $G^m$
such that
$G^m$
such that
![]() $\{h_{\alpha }\,|\,\alpha \in {\mathbb {N}}^{(m)}\}\subseteq \{g_{\alpha }\,|\,\alpha \in \mathcal F^{(1)}\text { and }\alpha>\alpha _0\}$
and
$\{h_{\alpha }\,|\,\alpha \in {\mathbb {N}}^{(m)}\}\subseteq \{g_{\alpha }\,|\,\alpha \in \mathcal F^{(1)}\text { and }\alpha>\alpha _0\}$
and
![]() ${\mathop { \mathcal {R}{\text {-}\mathrm {lim}}}_{{\alpha \in {\mathbb {N}}^{(m)}}}} x_{h_{\alpha }}=x_0$
. In particular, there exists an
${\mathop { \mathcal {R}{\text {-}\mathrm {lim}}}_{{\alpha \in {\mathbb {N}}^{(m)}}}} x_{h_{\alpha }}=x_0$
. In particular, there exists an
![]() $h\in \{g_{\alpha }\,|\,\alpha \in \mathcal F^{(1)}\text { and }\alpha>\alpha _0\}$
for which
$h\in \{g_{\alpha }\,|\,\alpha \in \mathcal F^{(1)}\text { and }\alpha>\alpha _0\}$
for which
![]() $d(x_h,x_0)<\epsilon $
, a contradiction.
$d(x_h,x_0)<\epsilon $
, a contradiction.
Remark 6.3. Theorem 6.2 shows that IP-limits can be attained via
![]() $\mathcal R$
-limits. The following example demonstrates that this is not the case the other way around. Let
$\mathcal R$
-limits. The following example demonstrates that this is not the case the other way around. Let
![]() $G={\mathbb {Z}}$
, let
$G={\mathbb {Z}}$
, let
![]() $X=\{0,1\}$
, let
$X=\{0,1\}$
, let
![]() $m\in {\mathbb {N}}$
and consider the
$m\in {\mathbb {N}}$
and consider the
![]() $\Sigma _m$
set
$\Sigma _m$
set
![]() $E=\{3^{k_1}+\cdots +3^{k_m}\,|\,k_1<\cdots <k_m\}$
. The set E is comprised of all the elements of
$E=\{3^{k_1}+\cdots +3^{k_m}\,|\,k_1<\cdots <k_m\}$
. The set E is comprised of all the elements of
![]() $3{\mathbb {N}}$
whose base 3 expansion has exactly m non-zero entries, all of which are 1. It follows that there are no
$3{\mathbb {N}}$
whose base 3 expansion has exactly m non-zero entries, all of which are 1. It follows that there are no
![]() $a,b,c\in E$
for which
$a,b,c\in E$
for which
![]() $a+b=c$
. This, in turn, implies that E contains no IP sets and hence
$a+b=c$
. This, in turn, implies that E contains no IP sets and hence
![]() ${\mathbb {Z}}\setminus E$
is an IP
${\mathbb {Z}}\setminus E$
is an IP
![]() $^*$
set. Let
$^*$
set. Let
![]() $(n_k)_{k\in {\mathbb {N}}}$
be a sequence in
$(n_k)_{k\in {\mathbb {N}}}$
be a sequence in
![]() ${\mathbb {Z}}$
and let
${\mathbb {Z}}$
and let
![]() $\mathcal F^{(1)}\subseteq \mathcal F$
be an
$\mathcal F^{(1)}\subseteq \mathcal F$
be an
![]() $\mathrm {IP}$
-ring for which
$\mathrm {IP}$
-ring for which
exists. Since
![]() $0\not \in E$
and
$0\not \in E$
and
![]() ${\mathbb {Z}}\setminus E$
is IP
${\mathbb {Z}}\setminus E$
is IP
![]() $^*$
, one has
$^*$
, one has
. On the other hand, since for any
![]() $k_1<\cdots <k_m$
,
$k_1<\cdots <k_m$
,
, one has that, for any infinite set
![]() $S\subseteq {\mathbb {N}}$
,
$S\subseteq {\mathbb {N}}$
,
Definition 6.4. Let
![]() $(G,+)$
be a countable abelian group and let
$(G,+)$
be a countable abelian group and let
![]() $(X,\mathcal A,\mu , (T_g)_{g\in G})$
be a measure-preserving system.
$(X,\mathcal A,\mu , (T_g)_{g\in G})$
be a measure-preserving system.
![]() $(T_g)_{g\in G}$
is mildly mixing if, for any sequence
$(T_g)_{g\in G}$
is mildly mixing if, for any sequence
![]() $(g_k)_{k\in {\mathbb {N}}}$
in G for which
$(g_k)_{k\in {\mathbb {N}}}$
in G for which
![]() $\lim _{\alpha \rightarrow \infty }g_{\alpha }=\infty $
, there exists an
$\lim _{\alpha \rightarrow \infty }g_{\alpha }=\infty $
, there exists an
![]() $\mathrm {IP}$
-ring
$\mathrm {IP}$
-ring
![]() $\mathcal F^{(1)}$
such that, for any
$\mathcal F^{(1)}$
such that, for any
![]() $f\in L^2(\mu )$
,
$f\in L^2(\mu )$
,
weakly.
We are now ready to state and prove the main theorem of this subsection. It can be viewed as an analogue of Theorem 3.1 for mildly mixing actions. We remind the reader that a sequence of measure-preserving transformations
![]() $(T_k)_{k\in {\mathbb {N}}}$
of a probability space
$(T_k)_{k\in {\mathbb {N}}}$
of a probability space
![]() $(X,\mathcal A,\mu )$
has the mixing property if, for every
$(X,\mathcal A,\mu )$
has the mixing property if, for every
![]() $A_0,A_1\in \mathcal A$
,
$A_0,A_1\in \mathcal A$
,
![]() $\lim _{k\rightarrow \infty }\mu (A_0\cap T_k^{-1}A_1)=\mu (A_0)\mu (A_1)$
.
$\lim _{k\rightarrow \infty }\mu (A_0\cap T_k^{-1}A_1)=\mu (A_0)\mu (A_1)$
.
Theorem 6.5. Let
![]() $\ell \in {\mathbb {N}}$
, let
$\ell \in {\mathbb {N}}$
, let
![]() $(G,+)$
be a countable abelian group and let
$(G,+)$
be a countable abelian group and let
![]() $(X,\mathcal A,\mu , (T_g)_{g\in G})$
be a measure-preserving system. The following statements are equivalent.
$(X,\mathcal A,\mu , (T_g)_{g\in G})$
be a measure-preserving system. The following statements are equivalent.
-
(i)
 $(T_g)_{g\in G}$
is mildly mixing.
$(T_g)_{g\in G}$
is mildly mixing. -
(ii) For any
 $\tilde {\text {IP}}$
set
$\tilde {\text {IP}}$
set
 $E\subseteq G^{\ell }$
and any
$E\subseteq G^{\ell }$
and any
 $m\in {\mathbb {N}}$
, there exist non-degenerated and essentially distinct sequences
$m\in {\mathbb {N}}$
, there exist non-degenerated and essentially distinct sequences
 $(\textbf g_k^{(j)})_{k\in {\mathbb {N}}}=(g_{k,1}^{(j)},\ldots ,g_{k,m}^{(j)})_{k\in {\mathbb {N}}}$
,
$(\textbf g_k^{(j)})_{k\in {\mathbb {N}}}=(g_{k,1}^{(j)},\ldots ,g_{k,m}^{(j)})_{k\in {\mathbb {N}}}$
,
 $j\in \{1,\ldots ,\ell \}$
, in
$j\in \{1,\ldots ,\ell \}$
, in
 $G^m$
with the following properties.
$G^m$
with the following properties.-
(a)
 $\{(g_{\alpha }^{(1)},\ldots ,g_{\alpha }^{(\ell )})\,|\,\alpha \in {\mathbb {N}}^{(m)}\}\subseteq E$
.
$\{(g_{\alpha }^{(1)},\ldots ,g_{\alpha }^{(\ell )})\,|\,\alpha \in {\mathbb {N}}^{(m)}\}\subseteq E$
. -
(b) For any
 $t\in \{1,\ldots ,m\}$
and any
$t\in \{1,\ldots ,m\}$
and any
 $j\in \{1,\ldots ,\ell \}$
,
$j\in \{1,\ldots ,\ell \}$
,
 $(T_{g_{k,t}^{(j)}})_{k\in {\mathbb {N}}}$
has the mixing property.
$(T_{g_{k,t}^{(j)}})_{k\in {\mathbb {N}}}$
has the mixing property. -
(c) For any t and any
 $i\neq j$
,
$i\neq j$
,
 $(T_{g_{k,t}^{(j)}-g_{k,t}^{(i)}})_{k\in {\mathbb {N}}}$
has the mixing property.
$(T_{g_{k,t}^{(j)}-g_{k,t}^{(i)}})_{k\in {\mathbb {N}}}$
has the mixing property.
-
-
(iii) For any
 $\tilde {\text {IP}}$
set
$\tilde {\text {IP}}$
set
 $E\subseteq G^{\ell }$
, there exist an
$E\subseteq G^{\ell }$
, there exist an
 $m\in {\mathbb {N}}$
and non-degenerated and essentially distinct sequences
$m\in {\mathbb {N}}$
and non-degenerated and essentially distinct sequences
 $(\textbf g_k^{(1)})_{k\in {\mathbb {N}}},\ldots ,(\textbf g_k^{(\ell )})_{k\in {\mathbb {N}}}$
in
$(\textbf g_k^{(1)})_{k\in {\mathbb {N}}},\ldots ,(\textbf g_k^{(\ell )})_{k\in {\mathbb {N}}}$
in
 $G^m$
with
$G^m$
with
 $\{(g_{\alpha }^{(1)},\ldots ,g_{\alpha }^{(\ell )})\,|\, \alpha \in {\mathbb {N}}^{(m)}\}\subseteq E$
and such that, for any
$\{(g_{\alpha }^{(1)},\ldots ,g_{\alpha }^{(\ell )})\,|\, \alpha \in {\mathbb {N}}^{(m)}\}\subseteq E$
and such that, for any
 $A_0,\ldots ,A_{\ell }\in \mathcal A$
, (6.5)
$A_0,\ldots ,A_{\ell }\in \mathcal A$
, (6.5) $$ \begin{align} {\mathop { \mathcal {R}{\text{-}\mathrm{lim}}}_{{\alpha\in {\mathbb{N}}^{(m)}}}}\, \mu(A_0\cap T_{g^{(1)}_{\alpha}} A_1\cap\cdots\cap T_{g^{(\ell)}_{\alpha}}A_{\ell})=\prod_{j=0}^{\ell}\mu(A_j). \end{align} $$
$$ \begin{align} {\mathop { \mathcal {R}{\text{-}\mathrm{lim}}}_{{\alpha\in {\mathbb{N}}^{(m)}}}}\, \mu(A_0\cap T_{g^{(1)}_{\alpha}} A_1\cap\cdots\cap T_{g^{(\ell)}_{\alpha}}A_{\ell})=\prod_{j=0}^{\ell}\mu(A_j). \end{align} $$
-
(iv) Given sequences
 $(g^{(1)}_k)_{k\in {\mathbb {N}}},\ldots,$
$(g^{(1)}_k)_{k\in {\mathbb {N}}},\ldots,$
 $(g^{(\ell )}_k)_{k\in {\mathbb {N}}}$
in G such that, for any
$(g^{(\ell )}_k)_{k\in {\mathbb {N}}}$
in G such that, for any
 $j\in \{1,\ldots ,\ell \}$
,
$j\in \{1,\ldots ,\ell \}$
,
 $\lim _{\alpha \rightarrow \infty }g^{(j)}_{\alpha }=\infty $
and, for any
$\lim _{\alpha \rightarrow \infty }g^{(j)}_{\alpha }=\infty $
and, for any
 $i\neq j$
,
$i\neq j$
,
 $\lim _{\alpha \rightarrow \infty }g_{\alpha }^{(j)}-g_{\alpha }^{(i)}=\infty $
(and so
$\lim _{\alpha \rightarrow \infty }g_{\alpha }^{(j)}-g_{\alpha }^{(i)}=\infty $
(and so
 ${E=\{(g_{\alpha }^{(1)},\ldots ,g_{\alpha }^{(\ell )})\,|\,\alpha \in \mathcal F\}}$
is an
${E=\{(g_{\alpha }^{(1)},\ldots ,g_{\alpha }^{(\ell )})\,|\,\alpha \in \mathcal F\}}$
is an
 $\tilde {\text {IP}}$
set), there exists an
$\tilde {\text {IP}}$
set), there exists an
 $\mathrm {IP}$
-ring
$\mathrm {IP}$
-ring
 $\mathcal F^{(1)}$
such that, for any
$\mathcal F^{(1)}$
such that, for any
 $A_0,\ldots ,A_{\ell } \in \mathcal A$
, (6.6)
$A_0,\ldots ,A_{\ell } \in \mathcal A$
, (6.6) $$ \begin{align} \mathop{\mathrm{IP}\text{-}\mathrm{lim}}_{\alpha\in\mathcal F^{(1)}}\mu(A_0\cap T_{g_{\alpha}^{(1)}}A_1\cap\cdots\cap T_{g_{\alpha}^{(\ell)}}A_{\ell})=\prod_{j=1}^{\ell} \mu(A_j). \end{align} $$
$$ \begin{align} \mathop{\mathrm{IP}\text{-}\mathrm{lim}}_{\alpha\in\mathcal F^{(1)}}\mu(A_0\cap T_{g_{\alpha}^{(1)}}A_1\cap\cdots\cap T_{g_{\alpha}^{(\ell)}}A_{\ell})=\prod_{j=1}^{\ell} \mu(A_j). \end{align} $$
-
(v) For any
 $A_0,\ldots ,A_{\ell }\in \mathcal A$
and any
$A_0,\ldots ,A_{\ell }\in \mathcal A$
and any
 $\epsilon>0$
, the set is an
$\epsilon>0$
, the set is an $$ \begin{align*}&R_{\epsilon}(A_0,\ldots,A_{\ell})\\&\quad=\bigg\{(g_1,\ldots,g_{\ell})\in G^{\ell}\,\bigg|\,\,\bigg|\mu(A_0\cap T_{g_1}A_1\cap\cdots \cap T_{g_{\ell}}A_{\ell})-\prod_{j=0}^{\ell} \mu( A_j)\bigg|<\epsilon\bigg\}\end{align*} $$
$$ \begin{align*}&R_{\epsilon}(A_0,\ldots,A_{\ell})\\&\quad=\bigg\{(g_1,\ldots,g_{\ell})\in G^{\ell}\,\bigg|\,\,\bigg|\mu(A_0\cap T_{g_1}A_1\cap\cdots \cap T_{g_{\ell}}A_{\ell})-\prod_{j=0}^{\ell} \mu( A_j)\bigg|<\epsilon\bigg\}\end{align*} $$
 $\tilde {\mathit {IP}}^{\mathrm {*}}$
set.
$\tilde {\mathit {IP}}^{\mathrm {*}}$
set.
Proof. (i)
![]() $\implies $
(ii): Let
$\implies $
(ii): Let
![]() $m\in {\mathbb {N}}$
, let
$m\in {\mathbb {N}}$
, let
![]() $E\subseteq G^{\ell }$
be an
$E\subseteq G^{\ell }$
be an
![]() $\tilde {\text {IP}}$
set and let the sequences
$\tilde {\text {IP}}$
set and let the sequences
![]() $(h_k^{(1)})_{k\in {\mathbb {N}}},\ldots ,(h_k^{(\ell )})_{k\in {\mathbb {N}}}$
in G be such that
$(h_k^{(1)})_{k\in {\mathbb {N}}},\ldots ,(h_k^{(\ell )})_{k\in {\mathbb {N}}}$
in G be such that
![]() $E=\{(h_{\alpha }^{(1)},\ldots ,h_{\alpha }^{(\ell )})\,|\,\alpha \in \mathcal F\}$
. By the stipulation made in Remark 5.2, for any
$E=\{(h_{\alpha }^{(1)},\ldots ,h_{\alpha }^{(\ell )})\,|\,\alpha \in \mathcal F\}$
. By the stipulation made in Remark 5.2, for any
![]() $\mathrm {IP}$
-ring
$\mathrm {IP}$
-ring
![]() $\mathcal F^{(1)}\subseteq \mathcal F$
, the set
$\mathcal F^{(1)}\subseteq \mathcal F$
, the set
![]() $\{(h^{(1)}_{\alpha },\ldots ,h^{(\ell )}_{\alpha })\,|\, \alpha \in \mathcal F^{(1)}\}$
is again an
$\{(h^{(1)}_{\alpha },\ldots ,h^{(\ell )}_{\alpha })\,|\, \alpha \in \mathcal F^{(1)}\}$
is again an
![]() $\tilde {\text {IP}}$
set. Pick
$\tilde {\text {IP}}$
set. Pick
![]() $\mathcal F^{(1)}$
to be an
$\mathcal F^{(1)}$
to be an
![]() $\mathrm {IP}$
-ring such that, for any
$\mathrm {IP}$
-ring such that, for any
![]() $A_0,A_1\in \mathcal A$
and any
$A_0,A_1\in \mathcal A$
and any
![]() $i,j\in \{1,\ldots ,\ell \}$
,
$i,j\in \{1,\ldots ,\ell \}$
,
exist. Let
![]() $(\alpha _k)_{k\in {\mathbb {N}}}$
be the sequence in
$(\alpha _k)_{k\in {\mathbb {N}}}$
be the sequence in
![]() $\mathcal F$
generating
$\mathcal F$
generating
![]() $\mathcal F^{(1)}$
(so, in particular,
$\mathcal F^{(1)}$
(so, in particular,
![]() $\alpha _k<\alpha _{k+1}$
for each
$\alpha _k<\alpha _{k+1}$
for each
![]() $k\in {\mathbb {N}}$
). It follows from (i) that each of the limits appearing in (6.7) equals
$k\in {\mathbb {N}}$
). It follows from (i) that each of the limits appearing in (6.7) equals
![]() $\mu (A_0)\mu (A_1)$
(otherwise, we would have a contradiction with formula (6.4)). Thus, for any
$\mu (A_0)\mu (A_1)$
(otherwise, we would have a contradiction with formula (6.4)). Thus, for any
![]() $A_0,A_1\in \mathcal A$
and any
$A_0,A_1\in \mathcal A$
and any
![]() $i,j\in \{1,\ldots ,\ell \}$
,
$i,j\in \{1,\ldots ,\ell \}$
,
 $$ \begin{align*}&\lim_{k\rightarrow\infty}\mu(A_0\cap T_{h^{(j)}_{\alpha_k}}A_1)\\&\quad=\mu(A_0)\mu(A_1)\quad\text{and, if } i\neq j,\quad\lim_{k\rightarrow\infty}\mu(A_0\cap T_{h^{(j)}_{\alpha_k}-h^{(i)}_{\alpha_k}}A_1)=\mu(A_0)\mu(A_1).\end{align*} $$
$$ \begin{align*}&\lim_{k\rightarrow\infty}\mu(A_0\cap T_{h^{(j)}_{\alpha_k}}A_1)\\&\quad=\mu(A_0)\mu(A_1)\quad\text{and, if } i\neq j,\quad\lim_{k\rightarrow\infty}\mu(A_0\cap T_{h^{(j)}_{\alpha_k}-h^{(i)}_{\alpha_k}}A_1)=\mu(A_0)\mu(A_1).\end{align*} $$
For each
![]() $j\in \{1,\ldots ,\ell \}$
, let
$j\in \{1,\ldots ,\ell \}$
, let
 $(\textbf g^{(j)}_k)_{k\in {\mathbb {N}}}=(\underbrace {h_{\alpha _k}^{(j)},\ldots ,h_{\alpha _k}^{(j)})}_{m\text { times}}$
. It is now easy to check that the sequences
$(\textbf g^{(j)}_k)_{k\in {\mathbb {N}}}=(\underbrace {h_{\alpha _k}^{(j)},\ldots ,h_{\alpha _k}^{(j)})}_{m\text { times}}$
. It is now easy to check that the sequences
![]() $(\textbf g^{(1)}_k)_{k\in {\mathbb {N}}},\ldots,$
$(\textbf g^{(1)}_k)_{k\in {\mathbb {N}}},\ldots,$
![]() $(\textbf g^{(\ell )}_k)_{k\in {\mathbb {N}}}$
are non-degenerated, essentially distinct, and satisfy (a)–(c), completing the proof of (i)
$(\textbf g^{(\ell )}_k)_{k\in {\mathbb {N}}}$
are non-degenerated, essentially distinct, and satisfy (a)–(c), completing the proof of (i)
![]() $\implies $
(ii).
$\implies $
(ii).
(ii)
![]() $\implies $
(iii): This follows from Proposition 2.9.
$\implies $
(iii): This follows from Proposition 2.9.
(iii)
![]() $\implies $
(iv): We will prove (iv) by applying Theorem 6.2 to the
$\implies $
(iv): We will prove (iv) by applying Theorem 6.2 to the
![]() $G^{\ell }$
-sequence
$G^{\ell }$
-sequence
and the sequence
![]() $(g_k^{(1)},\ldots ,g_k^{(\ell )})_{k\in {\mathbb {N}}}$
in
$(g_k^{(1)},\ldots ,g_k^{(\ell )})_{k\in {\mathbb {N}}}$
in
![]() $G^{\ell }$
.
$G^{\ell }$
.
Note that for any IP-ring
![]() $\mathcal F^{(2)}$
,
$\mathcal F^{(2)}$
,
![]() $\{(g_{\alpha }^{(1)},\ldots ,g_{\alpha }^{(\ell )})\,|\,\alpha \in \mathcal F^{(2)}\}$
is an
$\{(g_{\alpha }^{(1)},\ldots ,g_{\alpha }^{(\ell )})\,|\,\alpha \in \mathcal F^{(2)}\}$
is an
![]() $\tilde {\text {IP}}$
set. By (iii), there exist an
$\tilde {\text {IP}}$
set. By (iii), there exist an
![]() $m\in {\mathbb {N}}$
and non-degenerated and essentially distinct sequences
$m\in {\mathbb {N}}$
and non-degenerated and essentially distinct sequences
![]() $(\textbf h_k^{(1)})_{k\in {\mathbb {N}}},\ldots ,(\textbf h_k^{(\ell )})_{k\in {\mathbb {N}}}$
in
$(\textbf h_k^{(1)})_{k\in {\mathbb {N}}},\ldots ,(\textbf h_k^{(\ell )})_{k\in {\mathbb {N}}}$
in
![]() $G^m$
with
$G^m$
with
for which (6.5) holds. Letting
![]() $\mathcal F^{(1)}$
be an
$\mathcal F^{(1)}$
be an
![]() $\mathrm {IP}$
-ring for which the left-hand side of (6.6) exists for any
$\mathrm {IP}$
-ring for which the left-hand side of (6.6) exists for any
![]() $A_0,\ldots ,A_{\ell }\in \mathcal A$
, we obtain by Theorem 6.2 that (6.6) holds.
$A_0,\ldots ,A_{\ell }\in \mathcal A$
, we obtain by Theorem 6.2 that (6.6) holds.
(iv)
![]() $\implies $
(v): This implication follows from the definition of
$\implies $
(v): This implication follows from the definition of
![]() $\tilde {\text {IP}}^{\mathrm {*}}$
.
$\tilde {\text {IP}}^{\mathrm {*}}$
.
(v)
![]() $\implies $
(i): Let
$\implies $
(i): Let
![]() $(g_k)_{k\in {\mathbb {N}}}$
be a sequence in G with the property that
$(g_k)_{k\in {\mathbb {N}}}$
be a sequence in G with the property that
![]() $\lim _{\alpha \rightarrow \infty }g_{\alpha }=\infty $
. It suffices to show that, for some
$\lim _{\alpha \rightarrow \infty }g_{\alpha }=\infty $
. It suffices to show that, for some
![]() $\mathrm {IP}$
-ring
$\mathrm {IP}$
-ring
![]() $\mathcal F^{(1)}$
and any
$\mathcal F^{(1)}$
and any
![]() $A_0,A_1\in \mathcal A$
,
$A_0,A_1\in \mathcal A$
,
By (6.1), there exists an
![]() $\mathrm {IP}$
-ring
$\mathrm {IP}$
-ring
![]() $\mathcal F^{(1)}\subseteq \mathcal F$
such that, for any
$\mathcal F^{(1)}\subseteq \mathcal F$
such that, for any
![]() $A_0,A_1\in \mathcal A$
,
$A_0,A_1\in \mathcal A$
,
exists. Let
![]() $(\gamma _k)_{k\in {\mathbb {N}}}$
be a sequence in
$(\gamma _k)_{k\in {\mathbb {N}}}$
be a sequence in
![]() $\mathcal F^{(1)}$
with
$\mathcal F^{(1)}$
with
![]() $\gamma _k<\gamma _{k+1}$
, for each
$\gamma _k<\gamma _{k+1}$
, for each
![]() $k\in {\mathbb {N}}$
, and such that the sequences
$k\in {\mathbb {N}}$
, and such that the sequences
![]() $(h_k^{(j)})_{k\in {\mathbb {N}}}=(g_{\gamma _{j+\ell k}})_{k\in {\mathbb {N}}}$
,
$(h_k^{(j)})_{k\in {\mathbb {N}}}=(g_{\gamma _{j+\ell k}})_{k\in {\mathbb {N}}}$
,
![]() $j\in \{1,\ldots ,\ell \}$
, in G satisfy that (a) for any
$j\in \{1,\ldots ,\ell \}$
, in G satisfy that (a) for any
![]() $j\in \{1,\ldots ,\ell \}$
,
$j\in \{1,\ldots ,\ell \}$
,
![]() $\lim _{\alpha \rightarrow \infty }h_{\alpha }^{(j)}=\infty $
, and (b) for any
$\lim _{\alpha \rightarrow \infty }h_{\alpha }^{(j)}=\infty $
, and (b) for any
![]() $i\neq j$
,
$i\neq j$
,
![]() $\lim _{\alpha \rightarrow \infty }h_{\alpha }^{(j)}-h_{\alpha }^{(i)}=\infty $
. For each
$\lim _{\alpha \rightarrow \infty }h_{\alpha }^{(j)}-h_{\alpha }^{(i)}=\infty $
. For each
![]() $\alpha _0\in \mathcal F$
, let
$\alpha _0\in \mathcal F$
, let
Since
![]() $E_{\alpha _0}$
is an
$E_{\alpha _0}$
is an
![]() $\tilde {\text {IP}}$
set, (v) implies that, for any
$\tilde {\text {IP}}$
set, (v) implies that, for any
![]() $\alpha _0\in \mathcal F$
, any
$\alpha _0\in \mathcal F$
, any
![]() $A_0,A_1\in \mathcal A$
and any
$A_0,A_1\in \mathcal A$
and any
![]() $\epsilon>0$
,
$\epsilon>0$
,
Thus, for any
![]() $\alpha _0\in \mathcal F$
, there exists an
$\alpha _0\in \mathcal F$
, there exists an
![]() $\alpha>\alpha _0$
such that
$\alpha>\alpha _0$
such that
![]() $h^{(1)}_{\alpha }\in R_{\epsilon }(A_0,A_1)$
. Note that
$h^{(1)}_{\alpha }\in R_{\epsilon }(A_0,A_1)$
. Note that
 $$ \begin{align*}\lim_{\alpha\rightarrow\infty}\min\bigg(\bigcup_{k\in\alpha}\gamma_{1+\ell k}\bigg)=\infty.\end{align*} $$
$$ \begin{align*}\lim_{\alpha\rightarrow\infty}\min\bigg(\bigcup_{k\in\alpha}\gamma_{1+\ell k}\bigg)=\infty.\end{align*} $$
It follows that, for any
![]() $\beta _0\in \mathcal F$
, there is an
$\beta _0\in \mathcal F$
, there is an
![]() $\alpha \in \mathcal F$
such that
$\alpha \in \mathcal F$
such that
![]() $h_{\alpha }^{(1)}\in R_{\epsilon }(A_0,A_1)$
and such that
$h_{\alpha }^{(1)}\in R_{\epsilon }(A_0,A_1)$
and such that
![]() $\beta =\bigcup _{k\in \alpha }\gamma _{1+\ell k}\in \mathcal F^{(1)}$
satisfies
$\beta =\bigcup _{k\in \alpha }\gamma _{1+\ell k}\in \mathcal F^{(1)}$
satisfies
![]() $\beta>\beta _0$
. But
$\beta>\beta _0$
. But
![]() $g_{\beta }=g_{(\bigcup _{k\in \alpha }\gamma _{1+\ell k})}=h_{\alpha }^{(1)}$
, so
$g_{\beta }=g_{(\bigcup _{k\in \alpha }\gamma _{1+\ell k})}=h_{\alpha }^{(1)}$
, so
Since
![]() $\epsilon $
was arbitrary, for any
$\epsilon $
was arbitrary, for any
![]() $A_0,A_1\in \mathcal A$
,
$A_0,A_1\in \mathcal A$
,
which completes the proof.
Remark 6.6. We saw in §4 that the versatility of
![]() $\mathcal R$
-limits allows one to obtain from the multiparameter Theorem 3.1 some interesting results of diagonal nature. Similarly, one can obtain diagonal results from Theorem 6.5. For example, let
$\mathcal R$
-limits allows one to obtain from the multiparameter Theorem 3.1 some interesting results of diagonal nature. Similarly, one can obtain diagonal results from Theorem 6.5. For example, let
![]() $G={\mathbb {Z}}$
and assume that
$G={\mathbb {Z}}$
and assume that
![]() $(X,\mathcal A,\mu ,T)$
is a mildly mixing system. Then, by Theorem 6.5(iv), for any strictly increasing sequence
$(X,\mathcal A,\mu ,T)$
is a mildly mixing system. Then, by Theorem 6.5(iv), for any strictly increasing sequence
![]() $(n_k)_{k\in {\mathbb {N}}}$
in
$(n_k)_{k\in {\mathbb {N}}}$
in
![]() ${\mathbb {Z}}$
, any non-zero and distinct integers
${\mathbb {Z}}$
, any non-zero and distinct integers
![]() $a_1,\ldots ,a_{\ell }$
and any
$a_1,\ldots ,a_{\ell }$
and any
![]() $\mathrm {IP}$
-ring
$\mathrm {IP}$
-ring
![]() $\mathcal F^{(1)}\subseteq \mathcal F$
, there exists an
$\mathcal F^{(1)}\subseteq \mathcal F$
, there exists an
![]() $\mathrm {IP}$
-ring
$\mathrm {IP}$
-ring
![]() $\mathcal F^{(2)}\subseteq \mathcal F^{(1)}$
such that, for any
$\mathcal F^{(2)}\subseteq \mathcal F^{(1)}$
such that, for any
![]() $A_0,\ldots ,A_{\ell }\in \mathcal A$
,
$A_0,\ldots ,A_{\ell }\in \mathcal A$
,
 $$ \begin{align} \mathop{\mathrm{IP}\text{-}\mathrm{lim}}_{\alpha\in\mathcal F^{(2)}}\mu(A_0\cap T^{a_1n_{\alpha}}A_1\cap \cdots\cap T^{a_{\ell} n_{\alpha}}A_{\ell})=\prod_{j=0}^{\ell} \mu(A_j) \end{align} $$
$$ \begin{align} \mathop{\mathrm{IP}\text{-}\mathrm{lim}}_{\alpha\in\mathcal F^{(2)}}\mu(A_0\cap T^{a_1n_{\alpha}}A_1\cap \cdots\cap T^{a_{\ell} n_{\alpha}}A_{\ell})=\prod_{j=0}^{\ell} \mu(A_j) \end{align} $$
(cf. [Reference Furstenberg14, Theorem 9.27] and [Reference Furstenberg and Katznelson15, Theorem 5.4].)
6.2 Weakly mixing systems
This subsection is devoted to weakly mixing systems (which were introduced in §5.2) and has a similar structure to that of §6.1. We will first establish a technical lemma which connects
![]() $\mathcal R$
-limits with Césaro convergence. We will then prove an analogue of Theorem 3.1 (see Theorem 6.10 below) for weakly mixing systems and derive a corollary which has diagonal nature.
$\mathcal R$
-limits with Césaro convergence. We will then prove an analogue of Theorem 3.1 (see Theorem 6.10 below) for weakly mixing systems and derive a corollary which has diagonal nature.
Lemma 6.7. Let
![]() $(G,+)$
be a countable abelian group, let
$(G,+)$
be a countable abelian group, let
![]() $(X,d)$
be a compact metric space, let
$(X,d)$
be a compact metric space, let
![]() $(x_g)_{g\in G}$
be a sequence in X, let
$(x_g)_{g\in G}$
be a sequence in X, let
![]() $x_0\in X$
, let
$x_0\in X$
, let
![]() $(F_k)_{k\in {\mathbb {N}}}$
be a Følner sequence in G and let
$(F_k)_{k\in {\mathbb {N}}}$
be a Følner sequence in G and let
![]() $E\subseteq G$
be such that
$E\subseteq G$
be such that
![]() $\overline d_{(F_k)}(E)>0$
. The following statements are equivalent.
$\overline d_{(F_k)}(E)>0$
. The following statements are equivalent.
-
(i)
(6.10)
-
(ii) For any
 $D\subseteq E$
with
$D\subseteq E$
with
 $\overline d_{(F_k)}(D)>0$
, there exist an
$\overline d_{(F_k)}(D)>0$
, there exist an
 $m\in {\mathbb {N}}$
and a sequence
$m\in {\mathbb {N}}$
and a sequence
 $(g_{k,1},\ldots ,g_{k,m})_{k\in {\mathbb {N}}}$
in
$(g_{k,1},\ldots ,g_{k,m})_{k\in {\mathbb {N}}}$
in
 $G^m$
for which
$G^m$
for which
 $\{g_{\alpha }\,|\,\alpha \in {\mathbb {N}}^{(m)}\}\subseteq D$
and (6.11)
$\{g_{\alpha }\,|\,\alpha \in {\mathbb {N}}^{(m)}\}\subseteq D$
and (6.11) $$ \begin{align} {\mathop { \mathcal {R}{\text{-}\mathrm{lim}}}_{{\alpha\in{\mathbb{N}}^{(m)}}}}\, x_{g_{\alpha}}=x_0. \end{align} $$
$$ \begin{align} {\mathop { \mathcal {R}{\text{-}\mathrm{lim}}}_{{\alpha\in{\mathbb{N}}^{(m)}}}}\, x_{g_{\alpha}}=x_0. \end{align} $$
Proof. (i)
![]() $\implies $
(ii): Let
$\implies $
(ii): Let
![]() $D\subseteq E$
be such that
$D\subseteq E$
be such that
![]() $\overline d_{(F_k)}(D)>0$
. It follows from (6.10) that
$\overline d_{(F_k)}(D)>0$
. It follows from (6.10) that

Let
![]() $\epsilon>0$
. There exist infinitely many
$\epsilon>0$
. There exist infinitely many
![]() $g\in D$
such that
$g\in D$
such that
![]() $d(x_g,x_0)<\epsilon $
(otherwise, we would have
$d(x_g,x_0)<\epsilon $
(otherwise, we would have
). Thus, for each
![]() $k\in {\mathbb {N}}$
, there is a
$k\in {\mathbb {N}}$
, there is a
![]() $g_k\in D$
with
$g_k\in D$
with
![]() $d(x_{g_k},x_0)<{1}/{k}$
. It follows now that
$d(x_{g_k},x_0)<{1}/{k}$
. It follows now that
(ii)
![]() $\implies $
(i): It suffices to show that, for any given
$\implies $
(i): It suffices to show that, for any given
![]() $\epsilon>0$
,
$\epsilon>0$
,
![]() $\overline d_{(F_k)}(D_{\epsilon })=0$
, where
$\overline d_{(F_k)}(D_{\epsilon })=0$
, where
(This will imply that, for each
![]() $\epsilon>0$
,
$\epsilon>0$
,

Fix
![]() $\epsilon>0$
and suppose for contradiction that
$\epsilon>0$
and suppose for contradiction that
![]() $\overline d_{(F_k)}(D_{\epsilon })>0$
. It follows from (ii) that there exist an
$\overline d_{(F_k)}(D_{\epsilon })>0$
. It follows from (ii) that there exist an
![]() $m\in {\mathbb {N}}$
and a sequence
$m\in {\mathbb {N}}$
and a sequence
![]() $(g_{k,1},\ldots ,g_{k,m})_{k\in {\mathbb {N}}}$
in
$(g_{k,1},\ldots ,g_{k,m})_{k\in {\mathbb {N}}}$
in
![]() $G^m$
with
$G^m$
with
![]() $\{g_{\alpha }\,|\,\alpha \in {\mathbb {N}}^{(m)}\}\subseteq D_{\epsilon }$
for which (6.11) holds. In particular, for some
$\{g_{\alpha }\,|\,\alpha \in {\mathbb {N}}^{(m)}\}\subseteq D_{\epsilon }$
for which (6.11) holds. In particular, for some
![]() $g\in D_{\epsilon }$
,
$g\in D_{\epsilon }$
,
![]() $d(x_g,x_0)<\epsilon $
, which gives us the desired contradiction.
$d(x_g,x_0)<\epsilon $
, which gives us the desired contradiction.
We collect in the following proposition some equivalent definitions of weak mixing which will be needed for the proof of Theorem 6.10. The proof is totally analogous to the classical case
![]() $G={\mathbb {Z}}$
and is omitted.
$G={\mathbb {Z}}$
and is omitted.
Proposition 6.8. Let
![]() $(G,+)$
be a countable abelian group and let
$(G,+)$
be a countable abelian group and let
![]() $(X,\mathcal A,\mu , (T_g)_{g\in G})$
be a measure-preserving system. The following statements are equivalent.
$(X,\mathcal A,\mu , (T_g)_{g\in G})$
be a measure-preserving system. The following statements are equivalent.
-
(i)
 $(T_g)_{g\in G}$
is weakly mixing.
$(T_g)_{g\in G}$
is weakly mixing. -
(ii) For any ergodic probability measure-preserving system
 $(Y,\mathcal B,\nu , (S_g)_{g\in G})$
, the system is ergodic.
$(Y,\mathcal B,\nu , (S_g)_{g\in G})$
, the system is ergodic. $$ \begin{align*}(X\times Y,\mathcal A\otimes \mathcal B,\mu\otimes\nu, (T_g\times S_g)_{g\in G})\end{align*} $$
$$ \begin{align*}(X\times Y,\mathcal A\otimes \mathcal B,\mu\otimes\nu, (T_g\times S_g)_{g\in G})\end{align*} $$
-
(iii) For any Følner sequence
 $(F_k)_{k\in {\mathbb {N}}}$
in G there exists a set
$(F_k)_{k\in {\mathbb {N}}}$
in G there exists a set
 $B\subseteq G$
with
$B\subseteq G$
with
 $\overline d_{(F_k)}(B)=0$
such that, for any
$\overline d_{(F_k)}(B)=0$
such that, for any
 $A_0,A_1\in \mathcal A$
,
$A_0,A_1\in \mathcal A$
,  $$ \begin{align*}\lim_{g\rightarrow\infty,\,g\not\in B}\mu(A_0\cap T_gA_1)=\mu(A_0)\mu(A_1).\end{align*} $$
$$ \begin{align*}\lim_{g\rightarrow\infty,\,g\not\in B}\mu(A_0\cap T_gA_1)=\mu(A_0)\mu(A_1).\end{align*} $$
-
(iv) There exists a sequence
 $(g_k)_{k\in {\mathbb {N}}}$
in G with
$(g_k)_{k\in {\mathbb {N}}}$
in G with
 $\lim _{k\rightarrow \infty }g_k=\infty $
such that, for any
$\lim _{k\rightarrow \infty }g_k=\infty $
such that, for any
 $A_0,A_1\in \mathcal A$
,
$A_0,A_1\in \mathcal A$
,  $$ \begin{align*}\lim_{k\rightarrow\infty}\mu(A_0\cap T_{g_k}A_1)=\mu(A_0)\mu(A_1).\end{align*} $$
$$ \begin{align*}\lim_{k\rightarrow\infty}\mu(A_0\cap T_{g_k}A_1)=\mu(A_0)\mu(A_1).\end{align*} $$
Remark 6.9. It follows from (ii) that, for any two weakly mixing systems
![]() $(X,\mathcal A,\mu , (T_g)_{g\in G})$
and
$(X,\mathcal A,\mu , (T_g)_{g\in G})$
and
![]() $(Y,\mathcal B,\nu , (S_g)_{g\in G})$
,
$(Y,\mathcal B,\nu , (S_g)_{g\in G})$
,
![]() $(T_g\times S_g)$
is again weakly mixing.
$(T_g\times S_g)$
is again weakly mixing.
Theorem 6.10. Let
![]() $\ell \in {\mathbb {N}}$
, let
$\ell \in {\mathbb {N}}$
, let
![]() $(G,+)$
be a countable abelian group and let
$(G,+)$
be a countable abelian group and let
![]() $(X,\mathcal A,\mu , (T_g)_{g\in G})$
be a measure-preserving system. The following statements are equivalent.
$(X,\mathcal A,\mu , (T_g)_{g\in G})$
be a measure-preserving system. The following statements are equivalent.
-
(i)
 $(T_g)_{g\in G}$
is weakly mixing.
$(T_g)_{g\in G}$
is weakly mixing. -
(ii) For any Følner sequence
 $(F_k)_{k\in {\mathbb {N}}}$
in
$(F_k)_{k\in {\mathbb {N}}}$
in
 $G^{\ell }$
, any set
$G^{\ell }$
, any set
 $E\subseteq G^{\ell }$
with
$E\subseteq G^{\ell }$
with
 $\overline d_{(F_k)}(E)>0$
and any
$\overline d_{(F_k)}(E)>0$
and any
 $m\in {\mathbb {N}}$
, there exist non-degenerated and essentially distinct sequences
$m\in {\mathbb {N}}$
, there exist non-degenerated and essentially distinct sequences
 $(\textbf g_k^{(j)})_{k\in {\mathbb {N}}}=(g_{k,1}^{(j)},\ldots ,g_{k,m}^{(j)})_{k\in {\mathbb {N}}}$
,
$(\textbf g_k^{(j)})_{k\in {\mathbb {N}}}=(g_{k,1}^{(j)},\ldots ,g_{k,m}^{(j)})_{k\in {\mathbb {N}}}$
,
 $j\in \{1,\ldots ,\ell \}$
, in
$j\in \{1,\ldots ,\ell \}$
, in
 $G^m$
with the following properties.
$G^m$
with the following properties.-
(a)
 $\{(g_{\alpha }^{(1)},\ldots ,g_{\alpha }^{(\ell )})\,|\,\alpha \in {\mathbb {N}}^{(m)}\}\subseteq E$
.
$\{(g_{\alpha }^{(1)},\ldots ,g_{\alpha }^{(\ell )})\,|\,\alpha \in {\mathbb {N}}^{(m)}\}\subseteq E$
. -
(b) For any
 $t\in \{1,\ldots ,m\}$
and any
$t\in \{1,\ldots ,m\}$
and any
 $j\in \{1,\ldots ,\ell \}$
,
$j\in \{1,\ldots ,\ell \}$
,
 $(T_{g_{k,t}^{(j)}})_{k\in {\mathbb {N}}}$
has the mixing property.
$(T_{g_{k,t}^{(j)}})_{k\in {\mathbb {N}}}$
has the mixing property. -
(c) For any t and any
 $i\neq j$
,
$i\neq j$
,
 $(T_{g_{k,t}^{(j)}-g_{k,t}^{(i)}})_{k\in {\mathbb {N}}}$
has the mixing property.
$(T_{g_{k,t}^{(j)}-g_{k,t}^{(i)}})_{k\in {\mathbb {N}}}$
has the mixing property.
-
-
(iii) For any Følner sequence
 $(F_k)_{k\in {\mathbb {N}}}$
in
$(F_k)_{k\in {\mathbb {N}}}$
in
 $G^{\ell }$
and any set
$G^{\ell }$
and any set
 $E\subseteq G^{\ell }$
with
$E\subseteq G^{\ell }$
with
 $\overline d_{(F_k)} (E)>0$
, there exist an
$\overline d_{(F_k)} (E)>0$
, there exist an
 $m\in {\mathbb {N}}$
and sequences
$m\in {\mathbb {N}}$
and sequences
 $(\textbf g_k^{(1)})_{k\in {\mathbb {N}}},\ldots ,(\textbf g_k^{(\ell )})_{k\in {\mathbb {N}}}$
in
$(\textbf g_k^{(1)})_{k\in {\mathbb {N}}},\ldots ,(\textbf g_k^{(\ell )})_{k\in {\mathbb {N}}}$
in
 $G^m$
with
$G^m$
with
 $\{(g_{\alpha }^{(1)},\ldots ,g_{\alpha }^{(\ell )})\,|\,\alpha \in {\mathbb {N}}^{(m)}\}\subseteq E$
and such that, for any
$\{(g_{\alpha }^{(1)},\ldots ,g_{\alpha }^{(\ell )})\,|\,\alpha \in {\mathbb {N}}^{(m)}\}\subseteq E$
and such that, for any
 $A_0,\ldots ,A_{\ell }\in \mathcal A$
,
$A_0,\ldots ,A_{\ell }\in \mathcal A$
,  $$ \begin{align*} {\mathop { \mathcal {R}{\text{-}\mathrm{lim}}}_{{\alpha\in {\mathbb{N}}^{(m)}}}}\, \mu(A_0\cap T_{g^{(1)}_{\alpha}} A_1\cap\cdots\cap T_{g^{(\ell)}_{\alpha}}A_{\ell})=\prod_{j=0}^{\ell}\mu(A_j). \end{align*} $$
$$ \begin{align*} {\mathop { \mathcal {R}{\text{-}\mathrm{lim}}}_{{\alpha\in {\mathbb{N}}^{(m)}}}}\, \mu(A_0\cap T_{g^{(1)}_{\alpha}} A_1\cap\cdots\cap T_{g^{(\ell)}_{\alpha}}A_{\ell})=\prod_{j=0}^{\ell}\mu(A_j). \end{align*} $$
-
(iv) For any
 $A_0,\ldots ,A_{\ell }\in \mathcal A$
and any
$A_0,\ldots ,A_{\ell }\in \mathcal A$
and any
 $\epsilon>0$
, the set has uniform density one.
$\epsilon>0$
, the set has uniform density one. $$ \begin{align*} &R_{\epsilon}(A_0,\ldots,A_{\ell})\\ &\quad=\bigg\{(g_1,\ldots,g_{\ell})\in G^{\ell}\,\bigg|\,\,\bigg|\mu(A_0\cap T_{g_1}A_1\cap\cdots \cap T_{g_{\ell}}A_{\ell})-\prod_{j=0}^{\ell} \mu( A_j)\bigg|<\epsilon\bigg\} \end{align*} $$
$$ \begin{align*} &R_{\epsilon}(A_0,\ldots,A_{\ell})\\ &\quad=\bigg\{(g_1,\ldots,g_{\ell})\in G^{\ell}\,\bigg|\,\,\bigg|\mu(A_0\cap T_{g_1}A_1\cap\cdots \cap T_{g_{\ell}}A_{\ell})-\prod_{j=0}^{\ell} \mu( A_j)\bigg|<\epsilon\bigg\} \end{align*} $$
Proof. (i)
![]() $\implies $
(ii): For each
$\implies $
(ii): For each
![]() $j\in \{1,\ldots ,\ell \}$
, let
$j\in \{1,\ldots ,\ell \}$
, let
![]() $\pi _j:G^{\ell }\rightarrow G$
be defined by
$\pi _j:G^{\ell }\rightarrow G$
be defined by
![]() $\pi _j(g_1,\ldots , g_{\ell })=g_j$
. Note that
$\pi _j(g_1,\ldots , g_{\ell })=g_j$
. Note that
![]() $(T_{\pi _j(\textbf g)})_{\textbf g\in G^{\ell }}$
is a weakly mixing action and, for any
$(T_{\pi _j(\textbf g)})_{\textbf g\in G^{\ell }}$
is a weakly mixing action and, for any
![]() $i\neq j$
,
$i\neq j$
,
![]() $(T_{(\pi _j-\pi _i)(\textbf g)})_{\textbf g\in G^{\ell }}$
is also weakly mixing. Moreover (see Remark 6.9),
$(T_{(\pi _j-\pi _i)(\textbf g)})_{\textbf g\in G^{\ell }}$
is also weakly mixing. Moreover (see Remark 6.9),
 $$ \begin{align*} (S_{\textbf g})_{\textbf g\in G^{\ell}}=\bigg(\prod_{j=1}^{\ell} T_{\pi_j(\textbf g)}\times\prod_{i\neq j}T_{(\pi_j-\pi_i)(\textbf g)}\bigg)_{\textbf g\in G^{\ell}} \end{align*} $$
$$ \begin{align*} (S_{\textbf g})_{\textbf g\in G^{\ell}}=\bigg(\prod_{j=1}^{\ell} T_{\pi_j(\textbf g)}\times\prod_{i\neq j}T_{(\pi_j-\pi_i)(\textbf g)}\bigg)_{\textbf g\in G^{\ell}} \end{align*} $$
is a weakly mixing
![]() $G^{\ell }$
-action on the probability space
$G^{\ell }$
-action on the probability space
 $$ \begin{align*} \bigg(X^{\ell^2},\bigotimes_{j=1}^{\ell^2}\mathcal A,\nu\bigg), \end{align*} $$
$$ \begin{align*} \bigg(X^{\ell^2},\bigotimes_{j=1}^{\ell^2}\mathcal A,\nu\bigg), \end{align*} $$
where
![]() $\nu =\underbrace {\mu \times \cdots \times \mu }_{\ell ^2\text { times}}$
.
$\nu =\underbrace {\mu \times \cdots \times \mu }_{\ell ^2\text { times}}$
.
By Proposition 6.8(iii), there exists a set
![]() $B\subseteq G^{\ell }$
with
$B\subseteq G^{\ell }$
with
![]() $\overline d_{(F_k)}(B)=0$
such that, for any
$\overline d_{(F_k)}(B)=0$
such that, for any
![]() $A_0,A_1\in \bigotimes _{j=1}^{\ell ^2}\mathcal A$
,
$A_0,A_1\in \bigotimes _{j=1}^{\ell ^2}\mathcal A$
,
We start with proving (ii) for
![]() $m=1$
. Let
$m=1$
. Let
![]() $E\subseteq G^{\ell }$
with
$E\subseteq G^{\ell }$
with
![]() $\overline d_{(F_k)}(E)>0$
. By Proposition 5.8 (applied to
$\overline d_{(F_k)}(E)>0$
. By Proposition 5.8 (applied to
![]() $d=\ell $
,
$d=\ell $
,
![]() $m=1$
and the set
$m=1$
and the set
![]() $(E\setminus B)\subseteq G^{\ell }$
) there exist non-degenerated and essentially distinct sequences
$(E\setminus B)\subseteq G^{\ell }$
) there exist non-degenerated and essentially distinct sequences
![]() $(g_k^{(1)})_{k\in {\mathbb {N}}},\ldots ,(g_k^{(\ell )})_{k\in {\mathbb {N}}}$
in G with the property that, for each
$(g_k^{(1)})_{k\in {\mathbb {N}}},\ldots ,(g_k^{(\ell )})_{k\in {\mathbb {N}}}$
in G with the property that, for each
![]() $k\in {\mathbb {N}}$
,
$k\in {\mathbb {N}}$
,
![]() $\textbf g_k=(g_k^{(1)},\ldots ,g_k^{(\ell )})\in E\setminus B$
. It follows now from (6.12) that
$\textbf g_k=(g_k^{(1)},\ldots ,g_k^{(\ell )})\in E\setminus B$
. It follows now from (6.12) that
![]() $(S_{\textbf g_k})_{k\in {\mathbb {N}}}$
has the mixing property and hence, for any
$(S_{\textbf g_k})_{k\in {\mathbb {N}}}$
has the mixing property and hence, for any
![]() $j\in \{1,\ldots ,\ell \}$
,
$j\in \{1,\ldots ,\ell \}$
,
![]() $(T_{g_k^{(j)}})_{k\in {\mathbb {N}}}$
has the mixing property and, for any
$(T_{g_k^{(j)}})_{k\in {\mathbb {N}}}$
has the mixing property and, for any
![]() $i\neq j$
,
$i\neq j$
,
![]() $(T_{g_k^{(j)}-g_k^{(i)}})_{k\in {\mathbb {N}}}$
has the mixing property as well.
$(T_{g_k^{(j)}-g_k^{(i)}})_{k\in {\mathbb {N}}}$
has the mixing property as well.
Assume now that
![]() $m>1$
. Let
$m>1$
. Let
![]() $(g_k^{(1)})_{k\in {\mathbb {N}}},\ldots,$
$(g_k^{(1)})_{k\in {\mathbb {N}}},\ldots,$
![]() $(g_k^{(\ell )})_{k\in {\mathbb {N}}}$
be non-degenerated and essentially distinct sequences in G such that, for any distinct
$(g_k^{(\ell )})_{k\in {\mathbb {N}}}$
be non-degenerated and essentially distinct sequences in G such that, for any distinct
![]() $i,j\in \{1,\ldots ,\ell \}$
,
$i,j\in \{1,\ldots ,\ell \}$
,
![]() $(T_{g_k^{(j)}})_{k\in {\mathbb {N}}}$
and
$(T_{g_k^{(j)}})_{k\in {\mathbb {N}}}$
and
![]() $(T_{g_k^{(j)}-g_k^{(i)}})_{k\in {\mathbb {N}}}$
have the mixing property. Let
$(T_{g_k^{(j)}-g_k^{(i)}})_{k\in {\mathbb {N}}}$
have the mixing property. Let
![]() $(\textbf h_k)_{k\in {\mathbb {N}}}=(h^{(1)}_k,\ldots ,h^{(\ell )}_k)_{k\in {\mathbb {N}}}$
be a subsequence of
$(\textbf h_k)_{k\in {\mathbb {N}}}=(h^{(1)}_k,\ldots ,h^{(\ell )}_k)_{k\in {\mathbb {N}}}$
be a subsequence of
![]() $(g^{(1)}_k,\ldots ,g_k^{(\ell )})_{k\in {\mathbb {N}}}$
such that, for any
$(g^{(1)}_k,\ldots ,g_k^{(\ell )})_{k\in {\mathbb {N}}}$
such that, for any
![]() $i,j\in \{1,\ldots ,\ell \}$
,
$i,j\in \{1,\ldots ,\ell \}$
,
Observe that, by (6.13),
![]() $\{(h^{(1)}_{\alpha },\ldots ,h^{(\ell )}_{\alpha })\,|\,\alpha \in \mathcal F\}$
is an
$\{(h^{(1)}_{\alpha },\ldots ,h^{(\ell )}_{\alpha })\,|\,\alpha \in \mathcal F\}$
is an
![]() $\tilde {\text {IP}}$
set. It follows from our choice of
$\tilde {\text {IP}}$
set. It follows from our choice of
![]() $(g_k^{(1)})_{k\in {\mathbb {N}}},\ldots ,(g_k^{(\ell )})_{k\in {\mathbb {N}}}$
, that, for any
$(g_k^{(1)})_{k\in {\mathbb {N}}},\ldots ,(g_k^{(\ell )})_{k\in {\mathbb {N}}}$
, that, for any
![]() $M\in {\mathbb {N}}$
, any non-empty set
$M\in {\mathbb {N}}$
, any non-empty set
![]() $\alpha \subseteq \{1,\ldots ,M\}$
, any
$\alpha \subseteq \{1,\ldots ,M\}$
, any
![]() $A_0,A_1\in \mathcal A$
and any
$A_0,A_1\in \mathcal A$
and any
![]() $j\in \{1,\ldots ,\ell \}$
,
$j\in \{1,\ldots ,\ell \}$
,
and, for any
![]() $i\neq j$
,
$i\neq j$
,
Passing, if needed, to a subsequence of
![]() $(\textbf h_k)_{k\in {\mathbb {N}}}$
, we can derive now from (6.14) and (6.15) the following equations
$(\textbf h_k)_{k\in {\mathbb {N}}}$
, we can derive now from (6.14) and (6.15) the following equations
and, if
![]() $i\neq j$
,
$i\neq j$
,
We can conclude now the proof of (i)
![]() $\implies $
(ii) by arguing as in the proof of Proposition 5.8 and imitating the constructions in the proofs of Proposition 5.7 and Lemma 5.3.
$\implies $
(ii) by arguing as in the proof of Proposition 5.8 and imitating the constructions in the proofs of Proposition 5.7 and Lemma 5.3.
(ii)
![]() $\implies $
(iii): This follows from Proposition 2.9.
$\implies $
(iii): This follows from Proposition 2.9.
(iii)
![]() $\implies $
(iv): Let
$\implies $
(iv): Let
![]() $E=G^{\ell }\setminus R_{\epsilon }(A_0,\ldots ,A_{\ell })$
. It suffices to show that, for any Følner sequence
$E=G^{\ell }\setminus R_{\epsilon }(A_0,\ldots ,A_{\ell })$
. It suffices to show that, for any Følner sequence
![]() $(F_k)_{k\in {\mathbb {N}}}$
in
$(F_k)_{k\in {\mathbb {N}}}$
in
![]() $G^{\ell }$
,
$G^{\ell }$
,
![]() $\overline d_{(F_k)}(E)=0$
. To see this, note that if this was not the case, (iii) would imply that
$\overline d_{(F_k)}(E)=0$
. To see this, note that if this was not the case, (iii) would imply that
![]() $E\cap R_{\epsilon }(A_0,\ldots ,A_{\ell })\neq \emptyset $
, a contradiction.
$E\cap R_{\epsilon }(A_0,\ldots ,A_{\ell })\neq \emptyset $
, a contradiction.
(iv)
![]() $\implies $
(i): This implication is trivial and is omitted.
$\implies $
(i): This implication is trivial and is omitted.
We conclude this section with a corollary of Theorem 6.10 which has diagonal nature (this corollary can also be obtained from the main result in [Reference Bergelson and Rosenblatt6]).
Corollary 6.11. Let
![]() $(G,+)$
be a countable abelian group, let
$(G,+)$
be a countable abelian group, let
![]() $(X,\mathcal A,\mu ,(T_g)_{g\in G})$
be a measure-preserving system and let
$(X,\mathcal A,\mu ,(T_g)_{g\in G})$
be a measure-preserving system and let
![]() $\phi _1,\ldots ,\phi _{\ell }:G\rightarrow G$
be homomorphisms with the property that, for any
$\phi _1,\ldots ,\phi _{\ell }:G\rightarrow G$
be homomorphisms with the property that, for any
![]() $j\in \{1,\ldots ,\ell \}$
,
$j\in \{1,\ldots ,\ell \}$
,
![]() $(T_{\phi _j(g)})_{g\in G}$
is weakly mixing and, for any
$(T_{\phi _j(g)})_{g\in G}$
is weakly mixing and, for any
![]() $i\neq j$
,
$i\neq j$
,
![]() $(T_{(\phi _j-\phi _i)(g)})_{g\in G}$
is also weakly mixing. For any Følner sequence
$(T_{(\phi _j-\phi _i)(g)})_{g\in G}$
is also weakly mixing. For any Følner sequence
![]() $(F_k)_{k\in {\mathbb {N}}}$
in G and any
$(F_k)_{k\in {\mathbb {N}}}$
in G and any
![]() $A_0,\ldots ,A_{\ell }\in \mathcal A$
,
$A_0,\ldots ,A_{\ell }\in \mathcal A$
,
 $$ \begin{align} \lim_{k\rightarrow\infty}\frac{1}{|F_k|}\sum_{g\in F_k}\bigg|\mu(A_0\cap T_{\phi_1(g)}A_1\cap\cdots\cap T_{\phi_{\ell}(g)}A_{\ell})-\prod_{j=0}^{\ell} \mu(A_j)\bigg|=0. \end{align} $$
$$ \begin{align} \lim_{k\rightarrow\infty}\frac{1}{|F_k|}\sum_{g\in F_k}\bigg|\mu(A_0\cap T_{\phi_1(g)}A_1\cap\cdots\cap T_{\phi_{\ell}(g)}A_{\ell})-\prod_{j=0}^{\ell} \mu(A_j)\bigg|=0. \end{align} $$
Proof. By Lemma 6.7, in order to prove (6.16), it suffices to show that for any
![]() $E\subseteq G$
with
$E\subseteq G$
with
![]() $\overline d_{(F_k)}(E)>0$
, there exists a non-degenerated sequence
$\overline d_{(F_k)}(E)>0$
, there exists a non-degenerated sequence
![]() $(\textbf g_k)_{k\in {\mathbb {N}}}=(g_{k,1},\ldots ,g_{k,\ell })_{k\in {\mathbb {N}}}$
in
$(\textbf g_k)_{k\in {\mathbb {N}}}=(g_{k,1},\ldots ,g_{k,\ell })_{k\in {\mathbb {N}}}$
in
![]() $G^{\ell }$
with
$G^{\ell }$
with
![]() $\{g_{\alpha }\,|\,\alpha \in {\mathbb {N}}^{(\ell )}\}\subseteq E$
such that
$\{g_{\alpha }\,|\,\alpha \in {\mathbb {N}}^{(\ell )}\}\subseteq E$
such that
 $$ \begin{align} {\mathop { \mathcal {R}{\text{-}\mathrm{lim}}}_{{\alpha\in{\mathbb{N}}^{(\ell)}}}}\, \mu(A_0\cap T_{\phi_1(g_{\alpha})}A_1\cap\cdots\cap T_{\phi_{\ell}(g_{\alpha})}A_{\ell})=\prod_{j=0}^{\ell} \mu(A_j). \end{align} $$
$$ \begin{align} {\mathop { \mathcal {R}{\text{-}\mathrm{lim}}}_{{\alpha\in{\mathbb{N}}^{(\ell)}}}}\, \mu(A_0\cap T_{\phi_1(g_{\alpha})}A_1\cap\cdots\cap T_{\phi_{\ell}(g_{\alpha})}A_{\ell})=\prod_{j=0}^{\ell} \mu(A_j). \end{align} $$
By Theorem 6.10(ii), applied to the weakly mixing G-action
 $$ \begin{align*} (S_g)_{g\in G}=\bigg(\prod_{j=1}^{\ell} T_{\phi_j(g)}\times\prod_{i\neq j}T_{(\phi_j-\phi_i)(g)}\bigg)_{g\in G}, \end{align*} $$
$$ \begin{align*} (S_g)_{g\in G}=\bigg(\prod_{j=1}^{\ell} T_{\phi_j(g)}\times\prod_{i\neq j}T_{(\phi_j-\phi_i)(g)}\bigg)_{g\in G}, \end{align*} $$
there exists a non-degenerated sequence
![]() $(g_{k,1},\ldots ,g_{k,\ell })_{k\in {\mathbb {N}}}$
in G, with
$(g_{k,1},\ldots ,g_{k,\ell })_{k\in {\mathbb {N}}}$
in G, with
![]() $\{g_{\alpha }\,|\,\alpha \in {\mathbb {N}}^{(\ell )}\}\subseteq E$
, and such that, for any
$\{g_{\alpha }\,|\,\alpha \in {\mathbb {N}}^{(\ell )}\}\subseteq E$
, and such that, for any
![]() $t\in \{1,\ldots ,\ell \}$
, the sequence
$t\in \{1,\ldots ,\ell \}$
, the sequence
![]() $(S_{g_{k,t}})_{k\in {\mathbb {N}}}$
has the mixing property. It follows that for any
$(S_{g_{k,t}})_{k\in {\mathbb {N}}}$
has the mixing property. It follows that for any
![]() $t\in \{1,\ldots ,\ell \}$
and any
$t\in \{1,\ldots ,\ell \}$
and any
![]() $j\in \{1,\ldots ,\ell \}$
,
$j\in \{1,\ldots ,\ell \}$
,
![]() $(T_{\phi _j(g_{k,t})})_{k\in {\mathbb {N}}}$
has the mixing property and, for any t and
$(T_{\phi _j(g_{k,t})})_{k\in {\mathbb {N}}}$
has the mixing property and, for any t and
![]() $i\neq j$
,
$i\neq j$
,
![]() $(T_{(\phi _j-\phi _i)(g_{k,t})})_{k\in {\mathbb {N}}}$
has the mixing property as well. The result now follows from Proposition 2.9.
$(T_{(\phi _j-\phi _i)(g_{k,t})})_{k\in {\mathbb {N}}}$
has the mixing property as well. The result now follows from Proposition 2.9.
Remark 6.12. Taking in Corollary 6.11
![]() $G={\mathbb {Z}}$
, one obtains the following classical result due to Furstenberg (cf. [Reference Furstenberg14, Theorem 4.11]).
$G={\mathbb {Z}}$
, one obtains the following classical result due to Furstenberg (cf. [Reference Furstenberg14, Theorem 4.11]).
For any weakly mixing system
![]() $(X,\mathcal A,\mu , T)$
, any non-zero and distinct integers
$(X,\mathcal A,\mu , T)$
, any non-zero and distinct integers
![]() $a_1,\ldots ,a_{\ell }$
and any
$a_1,\ldots ,a_{\ell }$
and any
![]() $A_0,\ldots ,A_{\ell }\in \mathcal A$
,
$A_0,\ldots ,A_{\ell }\in \mathcal A$
,
 $$ \begin{align*} \lim_{N-M\rightarrow\infty}\frac{1}{N-M}\sum_{n=M+1}^N\bigg|\mu(A_0\cap T^{a_1n}A_1\cap \cdots\cap T^{a_{\ell} n}A_{\ell})-\prod_{j=0}^{\ell}\mu(A_j)\bigg|=0. \end{align*} $$
$$ \begin{align*} \lim_{N-M\rightarrow\infty}\frac{1}{N-M}\sum_{n=M+1}^N\bigg|\mu(A_0\cap T^{a_1n}A_1\cap \cdots\cap T^{a_{\ell} n}A_{\ell})-\prod_{j=0}^{\ell}\mu(A_j)\bigg|=0. \end{align*} $$