Hostname: page-component-76fb5796d-vfjqv Total loading time: 0 Render date: 2024-04-27T04:33:07.723Z Has data issue: false hasContentIssue false
  • English
  • Français

SRB measures for almost Axiom A diffeomorphisms

Published online by Cambridge University Press:  19 March 2015

JOSÉ F. ALVES  and
RENAUD LEPLAIDEUR
JOSÉ F. ALVES
Affiliation:
Departamento de Matemática, Faculdade de Ciências da Universidade do Porto, Rua do Campo Alegre 687, 4169-007 Porto, Portugal email jfalves@fc.up.pt
RENAUD LEPLAIDEUR
Affiliation:
LMBA UMR 6205, Université de Brest, 6 Av. Victor Le Gorgeu, C.S. 93837, 29238 Brest cedex 3, France email Renaud.Leplaideur@univ-brest.fr
Get access Rights & Permissions [Opens in a new window]

Abstract

We consider a diffeomorphism 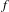$f$ of a compact manifold 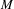$M$ which is almost Axiom A, i.e. 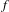$f$ is hyperbolic in a neighborhood of some compact 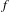$f$-invariant set, except in some singular set of neutral points. We prove that if there exists some $f$-invariant set of hyperbolic points with positive unstable Lebesgue measure such that for every point in this set the stable and unstable leaves are ‘long enough’, then 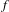$f$ admits an SRB (probability) measure.

Type
Research Article
Information
Ergodic Theory and Dynamical Systems , Volume 36 , Issue 7 , October 2016 , pp. 2015 - 2043
Copyright
© Cambridge University Press, 2015 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Alves, J. F.. SRB measures for non-hyperbolic systems with multidimensional expansion. Ann. Sci. Éc. Norm. Supér. (4) 33(1) (2000), 1–32.Google Scholar
Alves, J. F., Bonatti, C. and Viana, M.. SRB measures for partially hyperbolic systems whose central direction is mostly expanding. Invent. Math. 140 (2000), 351–398.Google Scholar
Benedicks, M. and Young, L.-S.. Sinai-Bowen-Ruelle measures for certain Hénon maps. Invent. Math. 112(3) (1993), 541–576.CrossRefGoogle Scholar
Bonatti, C., Díaz, L. J. and Pujals, E. R.. A C 1 -generic dichotomy for diffeomorphisms: weak forms of hyperbolicity or infinitely many sinks or sources. Ann. of Math. (2) 158(2) (2003), 355–418.CrossRefGoogle Scholar
Bonatti, C. and Viana, M.. SRB measures for partially hyperbolic systems whose central direction is mostly contracting. Israel J. Math. 115 (2000), 157–193.CrossRefGoogle Scholar
Bowen, R.. Equilibrium States and the Ergodic Theory of Anosov Diffeomorphisms (Lecture Notes in Mathematics, 470) . revised edn. Springer, Berlin, 2008, With a preface by David Ruelle. Edited by Jean–René Chazottes.Google Scholar
Hu, H.. Conditions for the existence of SBR measures for ‘almost Anosov’ diffeomorphisms. Trans. Amer. Math. Soc. 352(5) (2000), 2331–2367.CrossRefGoogle Scholar
Hu, H. and Young, L.-S.. Nonexistence of SBR-measures for some diffeomorphisms that are ‘almost Anosov’. Ergod. Th. & Dynam. Sys. 15(1) (1995), 67–76.Google Scholar
Ledrappier, F. and Young, L.-S.. The metric entropy of diffeomorphisms Part I: characterization of measures satisfying Pesin’s entropy formula. Ann. of Math. (2) 122 (1985), 509–539.CrossRefGoogle Scholar
Leplaideur, R.. Existence of SRB-measures for some topologically hyperbolic diffeomorphisms. Ergod. Th. & Dynam. Sys. 24(4) (2004), 1199–1225.CrossRefGoogle Scholar
Rohlin, V. A.. On the fundamental ideas of measure theory. Amer. Math. Soc. Transl. Ser. 2 10 (1962), 1–52.Google Scholar
Thaler, M.. Estimates of the invariant densities of endomorphisms with indifferent fixed points. Israel J. Math. 37(4) (1980), 303–314.CrossRefGoogle Scholar
Zweimüller, R.. Invariant measures for general(ized) induced transformations. Proc. Amer. Math. Soc. 133(8) (2005), 2283–2295 (electronic).Google Scholar