Hostname: page-component-76fb5796d-2lccl Total loading time: 0 Render date: 2024-04-27T15:16:04.334Z Has data issue: false hasContentIssue false
  • English
  • Français

Singular substitutions of constant length

Published online by Cambridge University Press:  18 January 2018

ARTEMI BERLINKOV  and
BORIS SOLOMYAK
ARTEMI BERLINKOV
Affiliation:
Department of Mathematics, Bar-Ilan University, Ramat-Gan, Israel email artem.berlinkov@gmail.com
BORIS SOLOMYAK
Affiliation:
Department of Mathematics, Bar-Ilan University, Ramat-Gan, Israel email bsolom3@gmail.com
Get access Rights & Permissions [Opens in a new window]

Abstract

We consider primitive aperiodic substitutions of constant length $q$ and prove that, in order to have a Lebesgue component in the spectrum of the associated dynamical system, it is necessary that one of the eigenvalues of the substitution matrix equals 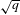$\sqrt{q}$ in absolute value. The proof is based on results of Queffélec combined with estimates of the local dimension of the spectral measure at zero.

Type
Original Article
Information
Ergodic Theory and Dynamical Systems , Volume 39 , Issue 9 , September 2019 , pp. 2384 - 2402
Copyright
© Cambridge University Press, 2018 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Adamczewski, B.. Symbolic discrepancy and self-similar dynamics. Ann. Inst. Fourier (Grenoble) 54 (2004), 2201–2234.Google Scholar
Aubry, S., Godrèche, C. and Luck, J. M.. Scaling properties of a structure intermediate between quasi-periodic and random. J. Stat. Phys. 51 (1988), 1033–1074.Google Scholar
Baake, M., Gähler, F. and Grimm, U.. Spectral and topological properties of a family of generalised Thue–Morse sequences. J. Math. Phys. 53(3) (2012), 032701.Google Scholar
Baake, M. and Grimm, U.. Aperiodic Order. Vol. 1, A Mathematical Invitation. With a Foreword by Roger Penrose (Encyclopedia of Mathematics and its Applications, 149) . Cambridge University Press, Cambridge, 2013.Google Scholar
Baake, M. and Grimm, U.. Squiral substitutions and beyond: substitution tilings with singular continuous spectrum. Ergod. Th. & Dynam. Sys. 34 (2014), 1077–1102.Google Scholar
Bartlett, A.. Spectral theory of ℤ d substitutions. Ergod. Th. & Dynam. Sys. to appear, published online 20 October 2016, doi:10.1017/etds.2016.66.Google Scholar
Bufetov, A. I.. Limit theorems for suspension flows over Vershik automorphisms. Russian Math. Surveys 68(5) (2013), 789–860.Google Scholar
Bufetov, A. I. and Solomyak, B.. Limit theorems for self-similar tilings. Comm. Math. Phys. 319 (2013), 761–789.Google Scholar
Bufetov, A. I. and Solomyak, B.. On the modulus of continuity for spectral measures in substitution dynamics. Adv. Math. 260 (2014), 84–129.Google Scholar
Chan, L. and Grimm, U.. Spectrum of a Rudin–Shapiro-like sequence. Adv. in Appl. Math. 87 (2017), 16–23.Google Scholar
Chan, L. and Grimm, U.. Substitution-based sequences with absolutely continuous diffraction. J. Phys.: Conf. Ser. 809(1) (2017), 012027.Google Scholar
Danilenko, A. I. and Lemańczyk, M.. Spectral multiplicities for ergodic flows. Discrete Contin. Dyn. Syst. 33(9) (2013), 4271–4289.Google Scholar
Dekking, F. M.. The spectrum of dynamical systems arising from substitutions of constant length. Z. Wahrscheinlichkeitsth. Verw. Geb. 41(3) (1977–1978), 221–239.Google Scholar
Dekking, F. M. and Keane, M.. Mixing properties of substitutions. Z. Wahrscheinlichkeitsth. Verw. Geb. 42 (1978), 23–33.Google Scholar
Durand, F.. A generalization of Cobham’s theorem. Theory Comput. Syst. 31(2) (1998), 169–185.Google Scholar
Emme, J.. Spectral measure at zero for self-similar tilings. Mosc. Math. J. 17(1) (2017), 35–49.Google Scholar
Frank, N. P.. Substitution sequences in ℤ d with a non-simple Lebesgue component in the spectrum. Ergod. Th. & Dynam. Sys. 23 (2003), 519–532.Google Scholar
Frank, N. P.. Multidimensional constant length substitution sequences. Topology Appl. 152 (2005), 44–69.Google Scholar
Godrèche, C. and Luck, J. M.. Multifractal analysis in reciprocal space and the nature of the Fourier transform of self-similar structures. J. Phys. A: Math. Gen. 23 (1990), 3769–3797.Google Scholar
Kakutani, S.. Strictly ergodic symbolic dynamical systems. Proc. 6th Berkeley Symp. Mathematical Statistics and Probability. Eds. LeCam, L. M., Neyman, J. and Scott, E. L.. University of California Press, Berkeley, CA, 1972, pp. 319–326.Google Scholar
Martin, J. C.. Substitution minimal flows. Amer. J. Math. 93 (1971), 503–526.Google Scholar
Pansiot, J.-J.. Decidability of periodicity for infinite words. RAIRO Théor. Inform. Appl. 20 (1986), 43–46.Google Scholar
Queffélec, M.. Substitution Dynamical Systems – Spectral Analysis (Lecture Notes in Mathematics, 1294) . 2nd edn. Springer, Berlin, 2010.Google Scholar
Siegel, A.. Spectral theory and geometric representation of substitutions. Substitutions in Dynamics, Arithmetics and Combinatorics (Lecture Notes in Mathematics, 1794) . Springer, Berlin, 2002, pp. 199–252.Google Scholar
Solomyak, B.. Dynamics of self-similar tilings. Ergod. Th. & Dynam. Sys. 17(3) (1997), 695–738.Google Scholar