Hostname: page-component-848d4c4894-x5gtn Total loading time: 0 Render date: 2024-05-01T11:22:00.702Z Has data issue: false hasContentIssue false
  • English
  • Français

Quasi-symmetric conjugacy for circle maps with a flat interval

Published online by Cambridge University Press:  20 June 2017

LIVIANA PALMISANO
LIVIANA PALMISANO*
Affiliation:
IMPAN, ul. Śniadeckich 8, 00-656 Warszawa, Poland email l.palmisano@impan.pl
Get access Rights & Permissions [Opens in a new window]

Abstract

In this paper we study quasi-symmetric conjugations of 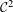${\mathcal{C}}^{2}$ weakly order-preserving circle maps with a flat interval. Under the assumption that the maps have the same rotation number of bounded type and that bounded geometry holds, we construct a quasi-symmetric conjugation between their non-wandering sets. Further, this conjugation is extended to a quasi-symmetric circle homeomorphism. Our proof techniques hinge on real-dynamic methods, allowing us to construct the conjugation under general and natural assumptions.

Type
Original Article
Information
Ergodic Theory and Dynamical Systems , Volume 39 , Issue 2 , February 2019 , pp. 425 - 445
Copyright
© Cambridge University Press, 2017 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Clark, T. and van Strien, S.. Quasisymmetric rigidity in one-dimensional dynamics. Manuscript.Google Scholar
Estevez, G. and de Faria, E.. Real bounds and quasisymmetric rigidity of multicritical circle maps. Trans. Amer. Math. Soc., to appear, https://doi.org/10.1090/tran/7177.Google Scholar
de Faria, E.. Quasisymmetric distortion and rigidity of expanding endomorphisms of S1 . Proc. Amer. Math. Soc. 124(6) (1996), 1949–1957.Google Scholar
de Faria, E. and de Melo, W.. Rigidity of critical circle mappings. I. J. Eur. Math. Soc. (JEMS) 1(4) (1999), 339–392.Google Scholar
de Melo, W. and van Strien, S.. One-dimensional Dynamics (Ergebnisse der Mathematik und ihrer Grenzgebiete (3), 25) . Springer, Berlin, 1993.Google Scholar
Graczyk, J.. Dynamics of circle maps with flat spots. Fund. Math. 209(3) (2010), 267–290.Google Scholar
Graczyk, J., Jonker, L. B., Świa̧tek, G., Tangerman, F. M. and Veerman, J. J. P.. Differentiable circle maps with a flat interval. Comm. Math. Phys. 173(3) (1995), 599–622.Google Scholar
Graczyk, J. and Świa̧tek, G.. Generic hyperbolicity in the logistic family. Ann. of Math. (2) 146(1) (1997), 1–52.Google Scholar
Heinonen, J.. Lectures on Analysis on Metric Spaces (Universitext) . Springer, New York, 2001.Google Scholar
Jakobson, M.. Quasisymmetric conjugacies for some one-dimensional maps inducing expansion. Symbolic Dynamics and its Applications (New Haven, CT, 1991) . American Mathematical Society, Providence, RI, 1992, pp. 203–211.Google Scholar
Jakobson, M. and Świa̧tek, G.. Metric properties of non-renormalizable S-unimodal maps. II. Quasisymmetric conjugacy classes. Ergod. Th. & Dynam. Sys. 15(5) (1995), 871–938.Google Scholar
Kozlovski, O., Shen, W. and van Strien, S.. Density of hyperbolicity in dimension one. Ann. of Math. (2) 166(1) (2007), 145–182.Google Scholar
Levin, G. and van Strien, S.. Bounds for maps of an interval with one critical point of inflection type. II. Invent. Math. 141(2) (2000), 399–465.Google Scholar
Lyubich, M.. Dynamics of quadratic polynomials. I. Acta Math. 178(2) (1997), 185–247.Google Scholar
Lyubich, M.. Dynamics of quadratic polynomials. II. Acta Math. 178(2) (1997), 247–297.Google Scholar
Martens, M., van Strien, S., de Melo, W. and Mendes, P.. On Cherry flows. Ergod. Th. & Dynam. Sys. 10(3) (1990), 531–554.Google Scholar
Moreira, P. C. and Ruas, A. A. G.. Metric properties of Cherry flows. J. Differential Equations 97(1) (1992), 16–26.Google Scholar
Palmisano, L.. A phase transition for circle maps and cherry flows. Comm. Math. Phys. 321(1) (2013), 135–155.Google Scholar
Palmisano, L.. Unbounded regime for circle maps with a flat interval. Discrete Contin. Dyn. Syst. 35(5) (2015), 2099–2122.Google Scholar
Sullivan, D.. Quasiconformal homeomorphisms in dynamics, topology, and geometry. Proc. Int. Congress Mathematicians, Vols 1, 2 (Berkeley, CA, 1986). American Mathematical Society, Providence, RI, 1987, pp. 1216–1228.Google Scholar
Świa̧tek, G.. Rational rotation numbers for maps of the circle. Comm. Math. Phys. 119(1) (1988), 109–128.Google Scholar
Tangerman, F. M. and Veerman, J. J. P.. Scalings in circle maps. II. Comm. Math. Phys. 141(2) (1991), 279–291.Google Scholar
Veerman, J. J. P. and Tangerman, F. M.. Scalings in circle maps. I. Comm. Math. Phys. 134(1) (1990), 89–107.Google Scholar
Yoccoz, J.-C.. Conjugaison analytique des difféomorphismes du cercle. Manuscript, 1989.Google Scholar