Article contents
Optimal lower bounds for multiple recurrence
Published online by Cambridge University Press: 07 October 2019
Abstract
Let 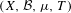 $(X,{\mathcal{B}},\unicode[STIX]{x1D707},T)$ be an ergodic measure-preserving system, let
$(X,{\mathcal{B}},\unicode[STIX]{x1D707},T)$ be an ergodic measure-preserving system, let 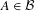 $A\in {\mathcal{B}}$ and let
$A\in {\mathcal{B}}$ and let 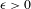 $\unicode[STIX]{x1D716}>0$. We study the largeness of sets of the form
$\unicode[STIX]{x1D716}>0$. We study the largeness of sets of the form 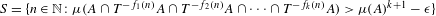 $$\begin{eqnarray}S=\{n\in \mathbb{N}:\unicode[STIX]{x1D707}(A\cap T^{-f_{1}(n)}A\cap T^{-f_{2}(n)}A\cap \cdots \cap T^{-f_{k}(n)}A)>\unicode[STIX]{x1D707}(A)^{k+1}-\unicode[STIX]{x1D716}\}\end{eqnarray}$$
$$\begin{eqnarray}S=\{n\in \mathbb{N}:\unicode[STIX]{x1D707}(A\cap T^{-f_{1}(n)}A\cap T^{-f_{2}(n)}A\cap \cdots \cap T^{-f_{k}(n)}A)>\unicode[STIX]{x1D707}(A)^{k+1}-\unicode[STIX]{x1D716}\}\end{eqnarray}$$ $\{f_{1},\ldots ,f_{k}\}$ of sequences
$\{f_{1},\ldots ,f_{k}\}$ of sequences 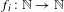 $f_{i}:\mathbb{N}\rightarrow \mathbb{N}$. For
$f_{i}:\mathbb{N}\rightarrow \mathbb{N}$. For 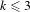 $k\leq 3$ and
$k\leq 3$ and 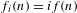 $f_{i}(n)=if(n)$, we show that
$f_{i}(n)=if(n)$, we show that  $S$ has positive density if
$S$ has positive density if 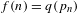 $f(n)=q(p_{n})$, where
$f(n)=q(p_{n})$, where 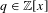 $q\in \mathbb{Z}[x]$ satisfies
$q\in \mathbb{Z}[x]$ satisfies 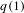 $q(1)$ or
$q(1)$ or 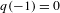 $q(-1)=0$ and
$q(-1)=0$ and 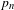 $p_{n}$ denotes the
$p_{n}$ denotes the  $n$th prime; or when
$n$th prime; or when 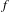 $f$ is a certain Hardy field sequence. If
$f$ is a certain Hardy field sequence. If 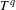 $T^{q}$ is ergodic for some
$T^{q}$ is ergodic for some 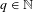 $q\in \mathbb{N}$, then, for all
$q\in \mathbb{N}$, then, for all 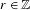 $r\in \mathbb{Z}$,
$r\in \mathbb{Z}$,  $S$ is syndetic if
$S$ is syndetic if 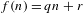 $f(n)=qn+r$. For
$f(n)=qn+r$. For 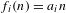 $f_{i}(n)=a_{i}n$, where
$f_{i}(n)=a_{i}n$, where 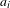 $a_{i}$ are distinct integers, we show that
$a_{i}$ are distinct integers, we show that  $S$ can be empty for
$S$ can be empty for 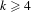 $k\geq 4$, and, for
$k\geq 4$, and, for 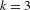 $k=3$, we found an interesting relation between the largeness of
$k=3$, we found an interesting relation between the largeness of  $S$ and the abundance of solutions to certain linear equations in sparse sets of integers. We also provide some partial results when the
$S$ and the abundance of solutions to certain linear equations in sparse sets of integers. We also provide some partial results when the 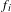 $f_{i}$ are distinct polynomials.
$f_{i}$ are distinct polynomials.
- Type
- Original Article
- Information
- Copyright
- © Cambridge University Press, 2019
References
- 3
- Cited by





