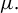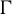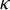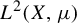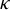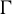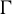1 Introduction
Let
![]() $\Gamma $
be a countable group acting measurably on a probability space
$\Gamma $
be a countable group acting measurably on a probability space
![]() $(X,\mu )$
by measure-preserving transformations. Let
$(X,\mu )$
by measure-preserving transformations. Let
![]() $\kappa =\kappa _{X}$
denote the corresponding Koopman representation of
$\kappa =\kappa _{X}$
denote the corresponding Koopman representation of
![]() $\Gamma $
, that is, the unitary representation of
$\Gamma $
, that is, the unitary representation of
![]() $\Gamma $
on
$\Gamma $
on
![]() $L^2(X,\mu )$
given by
$L^2(X,\mu )$
given by
We say that the action
![]() $\Gamma \curvearrowright (X,\mu )$
of
$\Gamma \curvearrowright (X,\mu )$
of
![]() $\Gamma $
on
$\Gamma $
on
![]() $(X,\mu )$
has a spectral gap if the restriction
$(X,\mu )$
has a spectral gap if the restriction
![]() $\kappa _0$
of
$\kappa _0$
of
![]() $\kappa $
to the
$\kappa $
to the
![]() $\Gamma $
-invariant subspace
$\Gamma $
-invariant subspace
 $$ \begin{align*} L^2_0(X,\mu)=\bigg\{\xi\in L^2(X,\mu) : \int_X \xi (x)\, d\mu (x)=0\bigg\} \end{align*} $$
$$ \begin{align*} L^2_0(X,\mu)=\bigg\{\xi\in L^2(X,\mu) : \int_X \xi (x)\, d\mu (x)=0\bigg\} \end{align*} $$
does not weakly contain the trivial representation
![]() $1_\Gamma $
; equivalently, if
$1_\Gamma $
; equivalently, if
![]() $\kappa _0$
does not have almost invariant vectors, that is, there is no sequence
$\kappa _0$
does not have almost invariant vectors, that is, there is no sequence
![]() $(\xi _n)_n$
of unit vectors in
$(\xi _n)_n$
of unit vectors in
![]() $ L^2_0(X,\mu )$
such that
$ L^2_0(X,\mu )$
such that
The existence of a spectral gap admits the following useful quantitative version. Let
![]() $\nu $
be a probability measure on
$\nu $
be a probability measure on
![]() $\Gamma $
and
$\Gamma $
and
![]() $\kappa _0(\nu )$
the convolution operator defined on
$\kappa _0(\nu )$
the convolution operator defined on
![]() $L^2_0(X,\mu )$
by
$L^2_0(X,\mu )$
by
 $$ \begin{align*} \kappa_0(\nu)\xi =\sum_{\gamma\in \Gamma} \nu(\gamma) \kappa_0(\gamma) \xi \quad\text{for all } \xi\in L^2_0(X,\mu). \end{align*} $$
$$ \begin{align*} \kappa_0(\nu)\xi =\sum_{\gamma\in \Gamma} \nu(\gamma) \kappa_0(\gamma) \xi \quad\text{for all } \xi\in L^2_0(X,\mu). \end{align*} $$
Observe that we have
![]() $\Vert \kappa _0(\nu ) \Vert \leq 1$
and hence
$\Vert \kappa _0(\nu ) \Vert \leq 1$
and hence
![]() $r(\kappa _0(\nu )) \leq 1$
for the spectral radius
$r(\kappa _0(\nu )) \leq 1$
for the spectral radius
![]() $r(\kappa _0(\nu ))$
of
$r(\kappa _0(\nu ))$
of
![]() $\kappa _0(\mu )$
. Assume that
$\kappa _0(\mu )$
. Assume that
![]() $\nu $
is aperiodic, that is, the support of
$\nu $
is aperiodic, that is, the support of
![]() $\nu $
is not contained in the coset of a proper subgroup of
$\nu $
is not contained in the coset of a proper subgroup of
![]() $\Gamma $
. Then the action of
$\Gamma $
. Then the action of
![]() $\Gamma $
on X has a spectral gap if and only if
$\Gamma $
on X has a spectral gap if and only if
![]() $r(\kappa _0(\nu ))<1$
and this is equivalent to
$r(\kappa _0(\nu ))<1$
and this is equivalent to
![]() $\Vert \kappa _0(\nu ) \Vert <1$
; for more details, see the survey [Reference Bekka and Guivarc’hBekk16].
$\Vert \kappa _0(\nu ) \Vert <1$
; for more details, see the survey [Reference Bekka and Guivarc’hBekk16].
In this paper we will be concerned with the case where X is an S-adic nilmanifold, to be introduced below, and
![]() $\Gamma $
is a subgroup of automorphisms of
$\Gamma $
is a subgroup of automorphisms of
![]() $X.$
$X.$
Fix a finite set
![]() $\{p_1, \ldots , p_r\}$
of integer primes and set
$\{p_1, \ldots , p_r\}$
of integer primes and set
![]() $S= \{p_1, \ldots , p_r, \infty \}$
. The product
$S= \{p_1, \ldots , p_r, \infty \}$
. The product
 $$ \begin{align*}\mathbf Q_S:= \prod_{p\in S} \mathbf Q_p= \mathbf Q_\infty\times\mathbf Q_{p_1}\times\cdots\times \mathbf Q_{p_r}\end{align*} $$
$$ \begin{align*}\mathbf Q_S:= \prod_{p\in S} \mathbf Q_p= \mathbf Q_\infty\times\mathbf Q_{p_1}\times\cdots\times \mathbf Q_{p_r}\end{align*} $$
is a locally compact ring, where
![]() $\mathbf Q_\infty = {\mathbf R}$
and
$\mathbf Q_\infty = {\mathbf R}$
and
![]() $\mathbf Q_p$
is the field of p-adic numbers for a prime p. Let
$\mathbf Q_p$
is the field of p-adic numbers for a prime p. Let
![]() ${\mathbf Z}[1/S]={\mathbf Z}[1/p_1, \cdots , 1/p_r]$
denote the subring of
${\mathbf Z}[1/S]={\mathbf Z}[1/p_1, \cdots , 1/p_r]$
denote the subring of
![]() $\mathbf Q$
generated by
$\mathbf Q$
generated by
![]() $1$
and
$1$
and
![]() $\{1/p_1, \ldots , 1/p_r\}.$
Through the diagonal embedding
$\{1/p_1, \ldots , 1/p_r\}.$
Through the diagonal embedding
we may identify
![]() ${\mathbf Z}[1/S]$
with a discrete and cocompact subring of
${\mathbf Z}[1/S]$
with a discrete and cocompact subring of
![]() $ \mathbf Q_S.$
$ \mathbf Q_S.$
If
![]() $\mathbf {G}$
is a linear algebraic group defined over
$\mathbf {G}$
is a linear algebraic group defined over
![]() $\mathbf Q,$
we denote by
$\mathbf Q,$
we denote by
![]() $\mathbf {G}(R)$
the group of elements of
$\mathbf {G}(R)$
the group of elements of
![]() $\mathbf {G}$
with coefficients in R and determinant invertible in
$\mathbf {G}$
with coefficients in R and determinant invertible in
![]() $R,$
for every subring R of an overfield of
$R,$
for every subring R of an overfield of
![]() $\mathbf Q.$
$\mathbf Q.$
Let
![]() $\mathbf {U}$
be a linear algebraic unipotent group defined over
$\mathbf {U}$
be a linear algebraic unipotent group defined over
![]() $\mathbf Q,$
that is,
$\mathbf Q,$
that is,
![]() $\mathbf {U}$
is an algebraic subgroup of the group of
$\mathbf {U}$
is an algebraic subgroup of the group of
![]() $n\times n$
upper triangular unipotent matrices for some
$n\times n$
upper triangular unipotent matrices for some
![]() $n\geq 1.$
The group
$n\geq 1.$
The group
![]() $\mathbf {U}(\mathbf Q_S)$
is a locally compact group and
$\mathbf {U}(\mathbf Q_S)$
is a locally compact group and
![]() $\Lambda :=\mathbf {U}({\mathbf Z}[1/S])$
is a cocompact lattice in
$\Lambda :=\mathbf {U}({\mathbf Z}[1/S])$
is a cocompact lattice in
![]() $\mathbf {U}(\mathbf Q_S)$
. The corresponding S-adic compact nilmanifold
$\mathbf {U}(\mathbf Q_S)$
. The corresponding S-adic compact nilmanifold
will be equipped with the unique translation-invariant probability measure
![]() $\mu $
on its Borel subsets.
$\mu $
on its Borel subsets.
For
![]() $p\in S,$
let
$p\in S,$
let
![]() $\mathrm {Aut}(\mathbf {U}(\mathbf Q_p))$
be the group of continuous automorphisms of
$\mathrm {Aut}(\mathbf {U}(\mathbf Q_p))$
be the group of continuous automorphisms of
![]() $\mathbf {U}(\mathbf Q_p).$
Set
$\mathbf {U}(\mathbf Q_p).$
Set
 $$ \begin{align*}\mathrm{Aut}(\mathbf{U}(\mathbf Q_S)):=\prod_{p\in S} \mathrm{ Aut}(\mathbf{U}( \mathbf Q_p))\end{align*} $$
$$ \begin{align*}\mathrm{Aut}(\mathbf{U}(\mathbf Q_S)):=\prod_{p\in S} \mathrm{ Aut}(\mathbf{U}( \mathbf Q_p))\end{align*} $$
and denote by
![]() $\mathrm {Aut} (\mathbf {Nil}_S)$
the subgroup
$\mathrm {Aut} (\mathbf {Nil}_S)$
the subgroup
Every
![]() $g\in \mathrm {Aut}(\mathbf {Nil}_S)$
acts on
$g\in \mathrm {Aut}(\mathbf {Nil}_S)$
acts on
![]() $\mathbf {Nil}_S$
preserving the probability measure
$\mathbf {Nil}_S$
preserving the probability measure
![]() $\mu .$
$\mu .$
The abelian quotient group
can be identified with
![]() $\mathbf Q_S^d$
for some
$\mathbf Q_S^d$
for some
![]() $d\geq 1$
and the image
$d\geq 1$
and the image
![]() $\Delta $
of
$\Delta $
of
![]() $\mathbf {U}({\mathbf Z}[1/S])$
in
$\mathbf {U}({\mathbf Z}[1/S])$
in
![]() $\overline {\mathbf {U}(\mathbf Q_S)}$
is a cocompact and discrete subgroup of
$\overline {\mathbf {U}(\mathbf Q_S)}$
is a cocompact and discrete subgroup of
![]() $\overline {\mathbf {U}(\mathbf Q_S)}$
; so,
$\overline {\mathbf {U}(\mathbf Q_S)}$
; so,
is a solenoid (that is, is a finite-dimensional, connected, compact abelian group; see [Reference Hewitt and RossHeRo63, §25]). We refer to
![]() $\mathbf {Sol}_S$
as the S-adic solenoid attached to the S- adic nilmanifold
$\mathbf {Sol}_S$
as the S-adic solenoid attached to the S- adic nilmanifold
![]() $\mathbf {Nil}_S.$
We equip
$\mathbf {Nil}_S.$
We equip
![]() $\mathbf {Sol}_S$
with the probability measure
$\mathbf {Sol}_S$
with the probability measure
![]() $\nu $
which is the image of
$\nu $
which is the image of
![]() $\mu $
under the canonical projection
$\mu $
under the canonical projection
![]() $\mathbf {Nil}_S\to \mathbf {Sol}_S.$
$\mathbf {Nil}_S\to \mathbf {Sol}_S.$
Observe that
![]() $\mathrm {Aut}(\mathbf Q_S^d)$
is canonically isomorphic to
$\mathrm {Aut}(\mathbf Q_S^d)$
is canonically isomorphic to
![]() $\prod _{s\in S}GL_d(\mathbf Q_{s})$
and that
$\prod _{s\in S}GL_d(\mathbf Q_{s})$
and that
![]() $\mathrm {Aut}(\mathbf {Sol}_S)$
can be identified with the subgroup
$\mathrm {Aut}(\mathbf {Sol}_S)$
can be identified with the subgroup
![]() $GL_d({\mathbf Z}[1/S]).$
The group
$GL_d({\mathbf Z}[1/S]).$
The group
![]() $\mathrm {Aut}(\mathbf {Nil}_S)$
acts naturally by automorphisms of
$\mathrm {Aut}(\mathbf {Nil}_S)$
acts naturally by automorphisms of
![]() $\mathbf {Sol}_S$
; we denote by
$\mathbf {Sol}_S$
; we denote by
the corresponding representation.
Theorem 1. Let
![]() $\mathbf {U}$
be an algebraic unipotent group defined over
$\mathbf {U}$
be an algebraic unipotent group defined over
![]() $\mathbf Q$
and
$\mathbf Q$
and
![]() $S= \{p_1, \ldots , p_r, \infty \},$
where
$S= \{p_1, \ldots , p_r, \infty \},$
where
![]() $p_1, \ldots , p_r$
are integer primes. Let
$p_1, \ldots , p_r$
are integer primes. Let
![]() $\mathbf {Nil}_S= \mathbf {U}(\mathbf Q_S)/\mathbf {U}({\mathbf Z}[1/S])$
be the associated S-adic nilmanifold and let
$\mathbf {Nil}_S= \mathbf {U}(\mathbf Q_S)/\mathbf {U}({\mathbf Z}[1/S])$
be the associated S-adic nilmanifold and let
![]() $\mathbf {Sol}_S$
be the corresponding S-adic solenoid, respectively equipped with the probability measures
$\mathbf {Sol}_S$
be the corresponding S-adic solenoid, respectively equipped with the probability measures
![]() $\mu $
and
$\mu $
and
![]() $\nu $
as above. Let
$\nu $
as above. Let
![]() $\Gamma $
be a countable subgroup of
$\Gamma $
be a countable subgroup of
![]() $\mathrm {Aut}(\mathbf {Nil}_S)$
. The following properties are equivalent.
$\mathrm {Aut}(\mathbf {Nil}_S)$
. The following properties are equivalent.
-
(i) The action
 $\Gamma \curvearrowright (\mathbf {Nil}_S,\mu )$
has a spectral gap.
$\Gamma \curvearrowright (\mathbf {Nil}_S,\mu )$
has a spectral gap. -
(ii) The action
 $p_S(\Gamma ) \curvearrowright (\mathbf {Sol}_S, \nu )$
has a spectral gap, where
$p_S(\Gamma ) \curvearrowright (\mathbf {Sol}_S, \nu )$
has a spectral gap, where
 $p_S: \mathrm {Aut}(\mathbf {Nil}_S)\to GL_d({\mathbf Z}[1/S])$
is the canonical homomorphism.
$p_S: \mathrm {Aut}(\mathbf {Nil}_S)\to GL_d({\mathbf Z}[1/S])$
is the canonical homomorphism.
Actions with spectral gap of groups of automorphisms (or more generally groups of affine transformations) of the S-adic solenoid
![]() $\mathbf {Sol}_S$
have been completely characterized in [Reference Bekka and FranciniBeFr20, Theorem 5]. The following result is an immediate consequence of this characterization and of Theorem 1. For a subset T of
$\mathbf {Sol}_S$
have been completely characterized in [Reference Bekka and FranciniBeFr20, Theorem 5]. The following result is an immediate consequence of this characterization and of Theorem 1. For a subset T of
![]() $GL_d(\mathbf K)$
for a field
$GL_d(\mathbf K)$
for a field
![]() $\mathbf K,$
we denote by
$\mathbf K,$
we denote by
![]() $T^t=\{g^t \mid g\in T\}$
the set of transposed matrices from T.
$T^t=\{g^t \mid g\in T\}$
the set of transposed matrices from T.
Corollary 2. With the notation as in Theorem 1, the following properties are equivalent.
-
(i) The action of
 $\Gamma $
on the S-adic nilmanifold
$\Gamma $
on the S-adic nilmanifold
 $\mathbf {Nil}_S$
does not have a spectral gap.
$\mathbf {Nil}_S$
does not have a spectral gap. -
(ii) There exists a non-zero linear subspace W of
 $\mathbf Q^d$
which is invariant under
$\mathbf Q^d$
which is invariant under
 $p_S(\Gamma )^t$
and such that the image of
$p_S(\Gamma )^t$
and such that the image of
 $p_S(\Gamma )^t$
in
$p_S(\Gamma )^t$
in
 $GL(W)$
is a virtually abelian group.
$GL(W)$
is a virtually abelian group.
Here is an immediate consequence of Corollary 2.
Corollary 3. With the notation as in Theorem 1, assume that the linear representation of
![]() $p_S(\Gamma)^t$
in
$p_S(\Gamma)^t$
in
![]() $\mathbf{Q}^d$
is irreducible and that
$\mathbf{Q}^d$
is irreducible and that
![]() $p_S(\Gamma)^t$
is not virtually abelian. Then the action
$p_S(\Gamma)^t$
is not virtually abelian. Then the action
![]() $\Gamma \curvearrowright (\mathbf {Nil}_S,\mu )$
has a spectral gap.
$\Gamma \curvearrowright (\mathbf {Nil}_S,\mu )$
has a spectral gap.
Recall that the action of a countable group
![]() $\Gamma $
by measure-preserving transformations on a probability space
$\Gamma $
by measure-preserving transformations on a probability space
![]() $(X, \mu )$
is strongly ergodic (see [Reference SchmidtSchm81]) if every sequence
$(X, \mu )$
is strongly ergodic (see [Reference SchmidtSchm81]) if every sequence
![]() $(B_n)_n$
of measurable subsets of X which is asymptotically invariant (that is, which is such that
$(B_n)_n$
of measurable subsets of X which is asymptotically invariant (that is, which is such that
![]() $\lim _n\mu (\gamma B_n \bigtriangleup B_n)=0$
for all
$\lim _n\mu (\gamma B_n \bigtriangleup B_n)=0$
for all
![]() $\gamma \in \Gamma $
) is trivial (that is,
$\gamma \in \Gamma $
) is trivial (that is,
![]() $\lim _n\mu ( B_n)(1-\mu (B_n))=0$
). It is straightforward to check that the spectral gap property implies strong ergodicity and it is known that the converse does not hold in general.
$\lim _n\mu ( B_n)(1-\mu (B_n))=0$
). It is straightforward to check that the spectral gap property implies strong ergodicity and it is known that the converse does not hold in general.
The following corollary is a direct consequence of Theorem 1 (compare with [Reference Bekka and HeuBeGu15, Corollary 2]).
Corollary 4. With the notation as in Theorem 1, the following properties are equivalent.
-
(i) The action
 $\Gamma \curvearrowright (\mathbf {Nil}_S,\mu )$
has the spectral gap property.
$\Gamma \curvearrowright (\mathbf {Nil}_S,\mu )$
has the spectral gap property. -
(ii) The action
 $\Gamma \curvearrowright (\mathbf {Nil}_S,\mu )$
is strongly ergodic.
$\Gamma \curvearrowright (\mathbf {Nil}_S,\mu )$
is strongly ergodic.
Theorem 1 generalizes our previous work [Reference Bekka and HeuBeGu15], where we treated the real case (that is, the case
![]() $S=\infty $
). This requires an extension of our methods to the S-adic setting, which is a non-straightforward task; more specifically, we had to establish the following four main tools for our proof:
$S=\infty $
). This requires an extension of our methods to the S-adic setting, which is a non-straightforward task; more specifically, we had to establish the following four main tools for our proof:
-
• a canonical decomposition of the Koopman representation of
 $\Gamma $
in
$\Gamma $
in
 $L^2(\mathbf {Nil}_S)$
as a direct sum of certain representations of
$L^2(\mathbf {Nil}_S)$
as a direct sum of certain representations of
 $\Gamma $
induced from stabilizers of representations of
$\Gamma $
induced from stabilizers of representations of
 $\mathbf {U}(\mathbf Q_S)$
—this fact is valid more generally for compact homogeneous spaces (see Proposition 9);
$\mathbf {U}(\mathbf Q_S)$
—this fact is valid more generally for compact homogeneous spaces (see Proposition 9); -
• a result of Howe and Moore [Reference Howe and TanHoMo79] about the decay of matrix coefficients of algebraic groups (see Proposition 11);
-
• the fact that the irreducible representations of
 $\mathbf {U}(\mathbf Q_S)$
appearing in the decomposition of
$\mathbf {U}(\mathbf Q_S)$
appearing in the decomposition of
 $L^2(\mathbf {Nil}_S)$
are rational, in the sense that the Kirillov data associated to each one of them are defined over
$L^2(\mathbf {Nil}_S)$
are rational, in the sense that the Kirillov data associated to each one of them are defined over
 $\mathbf Q$
(see Proposition 13);
$\mathbf Q$
(see Proposition 13); -
• a characterization (see Lemma 12) of the projective kernel of the extension of an irreducible representation of
 $\mathbf {U}(\mathbf Q_p)$
to its stabilizer in
$\mathbf {U}(\mathbf Q_p)$
to its stabilizer in
 $\mathrm { Aut}(\mathbf {U}(\mathbf Q_p).$
$\mathrm { Aut}(\mathbf {U}(\mathbf Q_p).$
Another tool we constantly use is a generalized version of Herz’s majoration principle (see Lemma 7).
Given a probability measure
![]() $\nu $
on
$\nu $
on
![]() $\Gamma ,$
our approach does not seem to provide quantitative estimates for the operator norm of the convolution operator
$\Gamma ,$
our approach does not seem to provide quantitative estimates for the operator norm of the convolution operator
![]() $\kappa _0(\nu )$
acting on
$\kappa _0(\nu )$
acting on
![]() $L^2_0(\mathbf {Nil}_S,\mu )$
for a general unipotent group
$L^2_0(\mathbf {Nil}_S,\mu )$
for a general unipotent group
![]() $\mathbf {U}.$
However, using known bounds for the so-called metaplectic representation of the symplectic group
$\mathbf {U}.$
However, using known bounds for the so-called metaplectic representation of the symplectic group
![]() $Sp_{2n}(\mathbf Q_p)$
, we give such estimates in the case of S-adic Heisenberg nilmanifolds (see §11).
$Sp_{2n}(\mathbf Q_p)$
, we give such estimates in the case of S-adic Heisenberg nilmanifolds (see §11).
Corollary 5. For an integer
![]() $n\geq 1,$
let
$n\geq 1,$
let
![]() $\mathbf {U}=\mathbf {H}_{2n+1}$
be the
$\mathbf {U}=\mathbf {H}_{2n+1}$
be the
![]() $(2n+1)$
-dimensional Heisenberg group and
$(2n+1)$
-dimensional Heisenberg group and
![]() $\mathbf {Nil}_S=\mathbf {H}_{2n+1}(\mathbf Q_S)/ \mathbf {H}_{2n+1}({\mathbf Z}[1/S]).$
Let
$\mathbf {Nil}_S=\mathbf {H}_{2n+1}(\mathbf Q_S)/ \mathbf {H}_{2n+1}({\mathbf Z}[1/S]).$
Let
![]() $\nu $
be a probability measure on the subgroup
$\nu $
be a probability measure on the subgroup
![]() $Sp_{2n}({\mathbf Z}[1/S])$
of
$Sp_{2n}({\mathbf Z}[1/S])$
of
![]() $\mathrm {Aut}(\mathbf {Nil}_S).$
Then
$\mathrm {Aut}(\mathbf {Nil}_S).$
Then
where
![]() $\kappa _1$
is the restriction of
$\kappa _1$
is the restriction of
![]() $\kappa _0$
to
$\kappa _0$
to
![]() $L^2_0(\mathbf {Sol}_S)$
and
$L^2_0(\mathbf {Sol}_S)$
and
![]() $\unicode{x3bb} _\Gamma $
is the regular representation of the group
$\unicode{x3bb} _\Gamma $
is the regular representation of the group
![]() $\Gamma $
generated by the support of
$\Gamma $
generated by the support of
![]() $\nu .$
In particular, in the case where
$\nu .$
In particular, in the case where
![]() $n=1$
and
$n=1$
and
![]() $\nu $
is aperiodic, the action of
$\nu $
is aperiodic, the action of
![]() $\Gamma $
on
$\Gamma $
on
![]() $\mathbf {Nil}_S$
has a spectral gap if and only if
$\mathbf {Nil}_S$
has a spectral gap if and only if
![]() $\Gamma $
is non-amenable.
$\Gamma $
is non-amenable.
2 Extension of representations
Let G be a locally compact group which we assume to be second countable. We will need the notion of a projective representation. Recall that a mapping
![]() $\pi : G \to U(\mathcal H)$
from G to the unitary group of the Hilbert space
$\pi : G \to U(\mathcal H)$
from G to the unitary group of the Hilbert space
![]() $\mathcal H$
is a projective representation of G if the following assertions hold.
$\mathcal H$
is a projective representation of G if the following assertions hold.
-
•
 $\pi (e)=I$
.
$\pi (e)=I$
. -
• For all
 $g_1,g_2\in G,$
there exists
$g_1,g_2\in G,$
there exists
 $c(g_1 , g_2 )\in \mathbf C $
such that
$c(g_1 , g_2 )\in \mathbf C $
such that  $$ \begin{align*} \pi(g_1 g_2 ) = c(g_1 , g_2 )\pi(g_1 )\pi(g_2). \end{align*} $$
$$ \begin{align*} \pi(g_1 g_2 ) = c(g_1 , g_2 )\pi(g_1 )\pi(g_2). \end{align*} $$
-
• The function
 $g\mapsto \langle \pi (g)\xi ,\eta \rangle $
is measurable for all
$g\mapsto \langle \pi (g)\xi ,\eta \rangle $
is measurable for all
 $\xi ,\eta \in \mathcal H.$
$\xi ,\eta \in \mathcal H.$
The mapping
![]() $c:G \times G \to {\mathbf S}^1$
is a
$c:G \times G \to {\mathbf S}^1$
is a
![]() $2$
-cocycle with values in the unit circle
$2$
-cocycle with values in the unit circle
![]() ${\mathbf S}^1.$
Every projective unitary representation of G can be lifted to an ordinary unitary representation of a central extension of
${\mathbf S}^1.$
Every projective unitary representation of G can be lifted to an ordinary unitary representation of a central extension of
![]() $G $
(for all this, see [Reference MackeyMack76] or [Reference MackeyMack58]).
$G $
(for all this, see [Reference MackeyMack76] or [Reference MackeyMack58]).
Let N be a closed normal subgroup of G. Let
![]() $\pi $
be an irreducible unitary representation of N on a Hilbert space
$\pi $
be an irreducible unitary representation of N on a Hilbert space
![]() $\mathcal H.$
Consider the stabilizer
$\mathcal H.$
Consider the stabilizer
of
![]() $\pi $
in G for the natural action of G on the unitary dual
$\pi $
in G for the natural action of G on the unitary dual
![]() $\widehat {N}$
given by
$\widehat {N}$
given by
![]() $\pi ^g(n)= \pi (g^{-1}n g).$
Then
$\pi ^g(n)= \pi (g^{-1}n g).$
Then
![]() $G_\pi $
is a closed subgroup of G containing
$G_\pi $
is a closed subgroup of G containing
![]() $N.$
The following lemma is a well-known part of Mackey’s theory of unitary representations of group extensions.
$N.$
The following lemma is a well-known part of Mackey’s theory of unitary representations of group extensions.
Lemma 6. Let
![]() $\pi $
be an irreducible unitary representation of N on the Hilbert space
$\pi $
be an irreducible unitary representation of N on the Hilbert space
![]() $\mathcal H.$
There exists a projective unitary representation
$\mathcal H.$
There exists a projective unitary representation
![]() $\widetilde \pi $
of
$\widetilde \pi $
of
![]() ${G}_{\pi }$
on
${G}_{\pi }$
on
![]() $\mathcal H$
which extends
$\mathcal H$
which extends
![]() $\pi $
. Moreover,
$\pi $
. Moreover,
![]() $ \widetilde \pi $
is unique, up to scalars: any other projective unitary representation
$ \widetilde \pi $
is unique, up to scalars: any other projective unitary representation
![]() $\widetilde \pi '$
of
$\widetilde \pi '$
of
![]() ${ G}_\pi $
extending
${ G}_\pi $
extending
![]() $\pi $
is of the form
$\pi $
is of the form
![]() $\widetilde \pi '=\unicode{x3bb} \widetilde \pi $
for a measurable function
$\widetilde \pi '=\unicode{x3bb} \widetilde \pi $
for a measurable function
![]() $\unicode{x3bb} : G_{\pi }\to {\mathbf S}^1.$
$\unicode{x3bb} : G_{\pi }\to {\mathbf S}^1.$
Proof. For every
![]() $g\in {G}_\pi $
, there exists a unitary operator
$g\in {G}_\pi $
, there exists a unitary operator
![]() $\widetilde \pi (g)$
on
$\widetilde \pi (g)$
on
![]() $\mathcal H$
such that
$\mathcal H$
such that
One can choose
![]() $\widetilde \pi (g)$
such that
$\widetilde \pi (g)$
such that
![]() $g\mapsto \widetilde \pi (g)$
is a projective unitary representation of
$g\mapsto \widetilde \pi (g)$
is a projective unitary representation of
![]() ${ G}_\pi $
which extends
${ G}_\pi $
which extends
![]() $\pi $
(see [Reference MackeyMack58, Theorem 8.2]). The uniqueness of
$\pi $
(see [Reference MackeyMack58, Theorem 8.2]). The uniqueness of
![]() $\pi $
follows from the irreducibility of
$\pi $
follows from the irreducibility of
![]() $\pi $
and Schur’s lemma.
$\pi $
and Schur’s lemma.
3 A weak containment result for induced representations
Let G be a locally compact group with Haar measure
![]() $\mu _G.$
Recall that a unitary representation
$\mu _G.$
Recall that a unitary representation
![]() $(\rho , \mathcal K)$
of G is weakly contained in another unitary representation
$(\rho , \mathcal K)$
of G is weakly contained in another unitary representation
![]() $(\pi , \mathcal H)$
of
$(\pi , \mathcal H)$
of
![]() $G,$
if every matrix coefficient
$G,$
if every matrix coefficient
of
![]() $\rho $
is the limit, uniformly over compact subsets of
$\rho $
is the limit, uniformly over compact subsets of
![]() $G,$
of a finite sum of matrix coefficients of
$G,$
of a finite sum of matrix coefficients of
![]() $\pi $
; equivalently, if
$\pi $
; equivalently, if
![]() $\Vert \rho (f)\Vert \leq \Vert \pi (f)\Vert $
for every
$\Vert \rho (f)\Vert \leq \Vert \pi (f)\Vert $
for every
![]() $f\in C_c(G),$
where
$f\in C_c(G),$
where
![]() $C_c(G)$
is the space of continuous functions with compact support on G and where the operator
$C_c(G)$
is the space of continuous functions with compact support on G and where the operator
![]() $\pi (f)\in \mathcal B(\mathcal H)$
is defined by the integral
$\pi (f)\in \mathcal B(\mathcal H)$
is defined by the integral
The trivial representation
![]() $1_G$
is weakly contained in
$1_G$
is weakly contained in
![]() $\pi $
if and only if there exists, for every compact subset Q of G and every
$\pi $
if and only if there exists, for every compact subset Q of G and every
![]() $\varepsilon>0,$
a unit vector
$\varepsilon>0,$
a unit vector
![]() $\xi \in \mathcal H$
which is
$\xi \in \mathcal H$
which is
![]() $(Q,\varepsilon )$
-invariant, that is, such that
$(Q,\varepsilon )$
-invariant, that is, such that
Let H be a closed subgroup of
![]() $G.$
We will always assume that the coset space
$G.$
We will always assume that the coset space
![]() $H\backslash G$
admits a non-zero G-invariant (possibly infinite) measure on its Borel subsets. Let
$H\backslash G$
admits a non-zero G-invariant (possibly infinite) measure on its Borel subsets. Let
![]() $(\sigma ,\mathcal K)$
be a unitary representation of
$(\sigma ,\mathcal K)$
be a unitary representation of
![]() $H.$
We will use the following model for the induced representation
$H.$
We will use the following model for the induced representation
![]() $\pi :=\mathrm {Ind}_H^G \sigma $
. Choose a Borel fundamental domain
$\pi :=\mathrm {Ind}_H^G \sigma $
. Choose a Borel fundamental domain
![]() $X\subset G$
for the action of G on
$X\subset G$
for the action of G on
![]() $H\backslash G$
. For
$H\backslash G$
. For
![]() $x \in X$
and
$x \in X$
and
![]() $g\in G,$
let
$g\in G,$
let
![]() $x\cdot g\in X$
and
$x\cdot g\in X$
and
![]() $c(x,g)\in H$
be defined by
$c(x,g)\in H$
be defined by
There exists a non-zero G-invariant measure on X for the action
![]() $(x,g)\mapsto x\cdot g$
of G on
$(x,g)\mapsto x\cdot g$
of G on
![]() $X.$
The Hilbert space of
$X.$
The Hilbert space of
![]() $\pi $
is the space
$\pi $
is the space
![]() $L^2(X, \mathcal K, \mu )$
of all square-integrable measurable mappings
$L^2(X, \mathcal K, \mu )$
of all square-integrable measurable mappings
![]() $\xi : X\to \mathcal K$
and the action of G on
$\xi : X\to \mathcal K$
and the action of G on
![]() $L^2(X, \mathcal K, \mu )$
is given by
$L^2(X, \mathcal K, \mu )$
is given by
Observe that, in the case where
![]() $\sigma $
is the trivial representation
$\sigma $
is the trivial representation
![]() $1_H,$
the induced representation
$1_H,$
the induced representation
![]() $\mathrm {Ind}_H^G1_H$
is equivalent to quasi-regular representation
$\mathrm {Ind}_H^G1_H$
is equivalent to quasi-regular representation
![]() $\unicode{x3bb} _{H\backslash G}$
, that is, the natural representation of G on
$\unicode{x3bb} _{H\backslash G}$
, that is, the natural representation of G on
![]() $L^2(H\backslash G,\mu )$
given by right translations.
$L^2(H\backslash G,\mu )$
given by right translations.
We will use several times the following elementary but crucial lemma, which can be viewed as a generalization of Herz’s majoration principle (see [Reference Bekka and HeuBeGu15, Proposition 17]).
Lemma 7. Let
![]() $(H_i)_{i\in I}$
be a family of closed subgroups of G such that
$(H_i)_{i\in I}$
be a family of closed subgroups of G such that
![]() $H_i\backslash G$
admits a non-zero G-invariant measure. Let
$H_i\backslash G$
admits a non-zero G-invariant measure. Let
![]() $(\sigma _i,\mathcal K_i)$
be a unitary representation of
$(\sigma _i,\mathcal K_i)$
be a unitary representation of
![]() $H_i.$
Assume that
$H_i.$
Assume that
![]() $1_G$
is weakly contained in the direct sum
$1_G$
is weakly contained in the direct sum
![]() $\bigoplus _{i\in I} \mathrm {Ind}_{H_i}^G\sigma _i$
. Then
$\bigoplus _{i\in I} \mathrm {Ind}_{H_i}^G\sigma _i$
. Then
![]() $1_G$
is weakly contained in
$1_G$
is weakly contained in
![]() $\bigoplus _{i\in I} \unicode{x3bb} _{H_i\backslash G}.$
$\bigoplus _{i\in I} \unicode{x3bb} _{H_i\backslash G}.$
Proof. Let Q be a compact subset of G and
![]() $\varepsilon>0.$
For every
$\varepsilon>0.$
For every
![]() $i\in I,$
let
$i\in I,$
let
![]() $X_i\subset G$
be a Borel fundamental domain for the action of G on
$X_i\subset G$
be a Borel fundamental domain for the action of G on
![]() $H_i\backslash G$
and
$H_i\backslash G$
and
![]() $\mu _i$
a non-zero G-invariant measure on
$\mu _i$
a non-zero G-invariant measure on
![]() $X_i.$
There exists a family of vectors
$X_i.$
There exists a family of vectors
![]() $\xi _i\in L^2(X_i, \mathcal K_i, \mu _i)$
such that
$\xi _i\in L^2(X_i, \mathcal K_i, \mu _i)$
such that
![]() $ \sum _{i}\Vert \xi _i\Vert ^2=1$
and
$ \sum _{i}\Vert \xi _i\Vert ^2=1$
and
Define
![]() $\varphi _i$
in
$\varphi _i$
in
![]() $L^2(X_i, \mu _i)$
by
$L^2(X_i, \mu _i)$
by
![]() $\varphi _i(x)=\Vert \xi _i(x)\Vert $
. Then
$\varphi _i(x)=\Vert \xi _i(x)\Vert $
. Then
![]() $ \sum _{i}\Vert \varphi _i\Vert ^2=1$
and, denoting by
$ \sum _{i}\Vert \varphi _i\Vert ^2=1$
and, denoting by
![]() $(x,g)\mapsto x\cdot _i g$
the action of G on
$(x,g)\mapsto x\cdot _i g$
the action of G on
![]() $X_i$
and by
$X_i$
and by
![]() $c_i:X_i\times G\to H_i$
the associated map as above, we have
$c_i:X_i\times G\to H_i$
the associated map as above, we have

for every
![]() $g\in G,$
and the claim follows.
$g\in G,$
and the claim follows.
4 Decay of matrix coefficients of unitary representations
We recall a few general facts about the decay of matrix coefficients of unitary representations, Recall that the projective kernel of a (genuine or projective) representation
![]() $\pi $
of the locally compact group G is the closed normal subgroup
$\pi $
of the locally compact group G is the closed normal subgroup
![]() $P_\pi $
of G consisting of the elements
$P_\pi $
of G consisting of the elements
![]() $g\in G$
such that
$g\in G$
such that
![]() $\pi (g)$
is a scalar multiple of the identity operator, that is, such that
$\pi (g)$
is a scalar multiple of the identity operator, that is, such that
![]() $\pi (g)=\unicode{x3bb} _\pi (g) I$
for some
$\pi (g)=\unicode{x3bb} _\pi (g) I$
for some
![]() $\unicode{x3bb} _\pi (g)\in {\mathbf S}^1.$
$\unicode{x3bb} _\pi (g)\in {\mathbf S}^1.$
Observe also that, for
![]() $\xi , \eta \in \mathcal H,$
the absolute value of the matrix coefficient
$\xi , \eta \in \mathcal H,$
the absolute value of the matrix coefficient
is constant on cosets modulo
![]() $P_\pi .$
For a real number p with
$P_\pi .$
For a real number p with
![]() $1\leq p <+\infty ,$
the representation
$1\leq p <+\infty ,$
the representation
![]() $\pi $
is said to be strongly
$\pi $
is said to be strongly
![]() $L^p$
modulo
$L^p$
modulo
![]() $P_\pi $
, if there is a dense subspace
$P_\pi $
, if there is a dense subspace
![]() $D\subset \mathcal H$
such that
$D\subset \mathcal H$
such that
![]() $|C^{\pi }_{\xi ,\eta }|\in L^p(G/P_\pi )$
for all
$|C^{\pi }_{\xi ,\eta }|\in L^p(G/P_\pi )$
for all
![]() $\xi ,\eta \in D.$
$\xi ,\eta \in D.$
Proposition 8. Assume that the unitary representation
![]() $\pi $
of the locally compact group G is strongly
$\pi $
of the locally compact group G is strongly
![]() $L^p$
modulo
$L^p$
modulo
![]() $P_\pi $
for
$P_\pi $
for
![]() $1\leq p <+\infty .$
Let k be an integer
$1\leq p <+\infty .$
Let k be an integer
![]() $k\geq p/2.$
Then the tensor power
$k\geq p/2.$
Then the tensor power
![]() $\pi ^{\otimes k} $
is contained in an infinite multiple of
$\pi ^{\otimes k} $
is contained in an infinite multiple of
![]() $\mathrm {Ind}_{P_\pi }^G \unicode{x3bb} _\pi ^k$
, where
$\mathrm {Ind}_{P_\pi }^G \unicode{x3bb} _\pi ^k$
, where
![]() $\unicode{x3bb} _\pi $
is the unitary character of
$\unicode{x3bb} _\pi $
is the unitary character of
![]() $P_\pi $
associated to
$P_\pi $
associated to
![]() $\pi .$
$\pi .$
Proof. Observe that
![]() $\sigma :=\pi ^{\otimes k}$
is square-integrable modulo
$\sigma :=\pi ^{\otimes k}$
is square-integrable modulo
![]() $P_\pi $
for every integer
$P_\pi $
for every integer
![]() $k\geq p/2.$
It follows (see [Reference Howe and TanHoMo79, Proposition 4.2] or [Reference HoweHoTa92, Ch. V, Proposition 1.2.3]) that
$k\geq p/2.$
It follows (see [Reference Howe and TanHoMo79, Proposition 4.2] or [Reference HoweHoTa92, Ch. V, Proposition 1.2.3]) that
![]() $\sigma $
is contained in an infinite multiple of
$\sigma $
is contained in an infinite multiple of
![]() $\mathrm {Ind}_{P_\sigma }^G \unicode{x3bb} _\sigma =\mathrm { Ind}_{P_\pi }^G \unicode{x3bb} _\pi ^k$
.
$\mathrm {Ind}_{P_\sigma }^G \unicode{x3bb} _\sigma =\mathrm { Ind}_{P_\pi }^G \unicode{x3bb} _\pi ^k$
.
5 The Koopman representation of the automorphism group of a homogeneous space
We establish a decomposition result for the Koopman representation of a group of automorphisms of an S-adic compact nilmanifold. We will state the result in the general context of a compact homogeneous space.
Let G be a locally compact group and
![]() $\Lambda $
a lattice in
$\Lambda $
a lattice in
![]() $G.$
We assume that
$G.$
We assume that
![]() $\Lambda $
is cocompact in
$\Lambda $
is cocompact in
![]() $G.$
The homogeneous space
$G.$
The homogeneous space
![]() $X:= G/\Lambda $
carries a probability measure
$X:= G/\Lambda $
carries a probability measure
![]() $\mu $
on the Borel subsets of X which is invariant by translations with elements from
$\mu $
on the Borel subsets of X which is invariant by translations with elements from
![]() $G.$
Every element from
$G.$
Every element from
induces a Borel isomorphism of X, which leaves
![]() $\mu $
invariant, as follows from the uniqueness of
$\mu $
invariant, as follows from the uniqueness of
![]() $\mu $
.
$\mu $
.
Given a subgroup
![]() $\Gamma $
of
$\Gamma $
of
![]() $\mathrm {Aut}(X),$
the following crucial proposition gives a decomposition of the associated Koopman
$\mathrm {Aut}(X),$
the following crucial proposition gives a decomposition of the associated Koopman
![]() $\Gamma $
on
$\Gamma $
on
![]() $L^2(X,\mu )$
as direct sum of certain induced representations of
$L^2(X,\mu )$
as direct sum of certain induced representations of
![]() $\Gamma $
.
$\Gamma $
.
Proposition 9. Let G be a locally compact group and
![]() $\Lambda $
a cocompact lattice in
$\Lambda $
a cocompact lattice in
![]() $G,$
and let
$G,$
and let
![]() $\Gamma $
be a countable subgroup of
$\Gamma $
be a countable subgroup of
![]() $\mathrm {Aut}(X)$
for
$\mathrm {Aut}(X)$
for
![]() $X:= G/\Lambda $
. Let
$X:= G/\Lambda $
. Let
![]() $\kappa $
denote the Koopman representation of
$\kappa $
denote the Koopman representation of
![]() $\Gamma $
associated to the action
$\Gamma $
associated to the action
![]() $\Gamma \curvearrowright X.$
There exists a family
$\Gamma \curvearrowright X.$
There exists a family
![]() $(\pi _i)_{i\in I}$
of irreducible unitary representations of G such that
$(\pi _i)_{i\in I}$
of irreducible unitary representations of G such that
![]() $\kappa $
is equivalent to a direct sum
$\kappa $
is equivalent to a direct sum
where
![]() $ \widetilde {\pi }_i$
is an irreducible projective representation of the stabilizer
$ \widetilde {\pi }_i$
is an irreducible projective representation of the stabilizer
![]() $G_i$
of
$G_i$
of
![]() $\pi _i$
in
$\pi _i$
in
![]() $\mathrm {Aut}(G)\ltimes G$
extending
$\mathrm {Aut}(G)\ltimes G$
extending
![]() $\pi _i$
, and where
$\pi _i$
, and where
![]() $W_i$
is a finite-dimensional projective unitary representation of
$W_i$
is a finite-dimensional projective unitary representation of
![]() $\Gamma _i :=\Gamma \cap G_i$
.
$\Gamma _i :=\Gamma \cap G_i$
.
Proof. We extend
![]() $\kappa $
to a unitary representation, again denoted by
$\kappa $
to a unitary representation, again denoted by
![]() $\kappa ,$
of
$\kappa ,$
of
![]() $\Gamma \ltimes G$
on
$\Gamma \ltimes G$
on
![]() $L^2(X,\mu )$
given by
$L^2(X,\mu )$
given by
Identifying
![]() $\Gamma $
and G with subgroups of
$\Gamma $
and G with subgroups of
![]() $\Gamma \ltimes G$
, we have
$\Gamma \ltimes G$
, we have
Since
![]() $\Lambda $
is cocompact in
$\Lambda $
is cocompact in
![]() $G,$
we can consider the decomposition of
$G,$
we can consider the decomposition of
![]() $L^2(X,\mu )$
into G-isotypical components: we have (see [Reference Gelfand, Graev and Pyatetskii-ShapiroGGPS69, Ch. I, §3, Theorem])
$L^2(X,\mu )$
into G-isotypical components: we have (see [Reference Gelfand, Graev and Pyatetskii-ShapiroGGPS69, Ch. I, §3, Theorem])
where
![]() $\Sigma $
is a certain set of pairwise non-equivalent irreducible unitary representations of G; for every
$\Sigma $
is a certain set of pairwise non-equivalent irreducible unitary representations of G; for every
![]() $\pi \in \Sigma $
, the space
$\pi \in \Sigma $
, the space
![]() $\mathcal H_{\pi }$
is the union of the closed
$\mathcal H_{\pi }$
is the union of the closed
![]() $\kappa (G)$
-invariant subspaces
$\kappa (G)$
-invariant subspaces
![]() $\mathcal K$
of
$\mathcal K$
of
![]() $\mathcal H:=L^2(X,\mu )$
for which the corresponding representation of G in
$\mathcal H:=L^2(X,\mu )$
for which the corresponding representation of G in
![]() ${\mathcal K}$
is equivalent to
${\mathcal K}$
is equivalent to
![]() $\pi $
; moreover, the multiplicity of every
$\pi $
; moreover, the multiplicity of every
![]() $\pi $
is finite, that is, every
$\pi $
is finite, that is, every
![]() $\mathcal H_{\pi }$
is a direct sum of finitely many irreducible unitary representations of G.
$\mathcal H_{\pi }$
is a direct sum of finitely many irreducible unitary representations of G.
Let
![]() $\gamma $
be a fixed automorphism in
$\gamma $
be a fixed automorphism in
![]() $\Gamma .$
Let
$\Gamma .$
Let
![]() $\kappa ^\gamma $
be the conjugate representation of
$\kappa ^\gamma $
be the conjugate representation of
![]() $\kappa $
by
$\kappa $
by
![]() $\gamma ,$
that is,
$\gamma ,$
that is,
![]() $ \kappa ^\gamma (g)=\kappa (\gamma g\gamma ^{-1})$
for all
$ \kappa ^\gamma (g)=\kappa (\gamma g\gamma ^{-1})$
for all
![]() $g\in \Gamma \ltimes G$
. On the one hand, for every
$g\in \Gamma \ltimes G$
. On the one hand, for every
![]() $\pi \in \Sigma ,$
the isotypical component of
$\pi \in \Sigma ,$
the isotypical component of
![]() $\kappa ^\gamma \vert _{G}$
corresponding to
$\kappa ^\gamma \vert _{G}$
corresponding to
![]() $\pi $
is
$\pi $
is
![]() $\mathcal H_{\pi ^{\gamma ^{-1}}}$
. On the other hand, relation
$\mathcal H_{\pi ^{\gamma ^{-1}}}$
. On the other hand, relation
![]() $(*)$
shows that
$(*)$
shows that
![]() $\kappa (\gamma )$
is a unitary equivalence between
$\kappa (\gamma )$
is a unitary equivalence between
![]() $\kappa \vert _{G} $
and
$\kappa \vert _{G} $
and
![]() $\kappa ^\gamma \vert _{G}.$
It follows that
$\kappa ^\gamma \vert _{G}.$
It follows that
so,
![]() $\Gamma $
permutes the
$\Gamma $
permutes the
![]() $\mathcal H_\pi $
s among themselves according to its action on
$\mathcal H_\pi $
s among themselves according to its action on
![]() $\widehat {G}.$
$\widehat {G}.$
Write
![]() $\Sigma =\bigcup _{i\in I} \Sigma _i,$
where the
$\Sigma =\bigcup _{i\in I} \Sigma _i,$
where the
![]() $\Sigma _i$
are the
$\Sigma _i$
are the
![]() $\Gamma $
-orbits in
$\Gamma $
-orbits in
![]() $\Sigma ,$
and set
$\Sigma ,$
and set
Every
![]() $\mathcal H_{\Sigma _i}$
is invariant under
$\mathcal H_{\Sigma _i}$
is invariant under
![]() $\Gamma \ltimes G$
and we have an orthogonal decomposition
$\Gamma \ltimes G$
and we have an orthogonal decomposition
Fix
![]() $i\in I.$
Choose a representation
$i\in I.$
Choose a representation
![]() ${\pi }_i $
in
${\pi }_i $
in
![]() $\Sigma _i$
and set
$\Sigma _i$
and set
![]() $\mathcal H_i= \mathcal H_{\pi _i}.$
Let
$\mathcal H_i= \mathcal H_{\pi _i}.$
Let
![]() $\Gamma _i$
denote the stabilizer of
$\Gamma _i$
denote the stabilizer of
![]() $\pi _i$
in
$\pi _i$
in
![]() $\Gamma .$
The space
$\Gamma .$
The space
![]() $\mathcal H_i$
is invariant under
$\mathcal H_i$
is invariant under
![]() $\Gamma _i.$
Let
$\Gamma _i.$
Let
![]() $V_i$
be the corresponding representation of
$V_i$
be the corresponding representation of
![]() $ \Gamma _i\ltimes G$
on
$ \Gamma _i\ltimes G$
on
![]() $\mathcal H_i.$
$\mathcal H_i.$
Choose a set
![]() $S_i$
of representatives for the cosets in
$S_i$
of representatives for the cosets in
with
![]() $e\in S_i.$
Then
$e\in S_i.$
Then
![]() $\Sigma _i=\{ \pi _i^s : s\in S_i\}$
and the Hilbert space
$\Sigma _i=\{ \pi _i^s : s\in S_i\}$
and the Hilbert space
![]() $\mathcal H_{\Sigma _i}$
is the sum of mutually orthogonal spaces:
$\mathcal H_{\Sigma _i}$
is the sum of mutually orthogonal spaces:
 $$ \begin{align*} \mathcal H_{\Sigma_i}= \bigoplus_{s\in S_i}\mathcal H_i^s. \end{align*} $$
$$ \begin{align*} \mathcal H_{\Sigma_i}= \bigoplus_{s\in S_i}\mathcal H_i^s. \end{align*} $$
Moreover,
![]() $\mathcal H_i^s$
is the image under
$\mathcal H_i^s$
is the image under
![]() $\kappa (s)$
of
$\kappa (s)$
of
![]() $\mathcal H_i$
for every
$\mathcal H_i$
for every
![]() $s\in S_i.$
This means that the restriction
$s\in S_i.$
This means that the restriction
![]() $\kappa _i$
of
$\kappa _i$
of
![]() $\kappa $
to
$\kappa $
to
![]() $\mathcal H_{\Sigma _i}$
of the Koopman representation
$\mathcal H_{\Sigma _i}$
of the Koopman representation
![]() $\kappa $
of
$\kappa $
of
![]() $\Gamma $
is equivalent to the induced representation
$\Gamma $
is equivalent to the induced representation
![]() $\mathrm {Ind}_{\Gamma _i}^{\Gamma } {V_i}.$
$\mathrm {Ind}_{\Gamma _i}^{\Gamma } {V_i}.$
Since every
![]() $\mathcal H_{i}$
is a direct sum of finitely many irreducible unitary representations of
$\mathcal H_{i}$
is a direct sum of finitely many irreducible unitary representations of
![]() $G,$
we can assume that
$G,$
we can assume that
![]() $\mathcal H_i$
is the tensor product
$\mathcal H_i$
is the tensor product
of the Hilbert space
![]() $\mathcal K_i$
of
$\mathcal K_i$
of
![]() $\pi _i$
with a finite-dimensional Hilbert space
$\pi _i$
with a finite-dimensional Hilbert space
![]() $\mathcal L_i,$
in such a way that
$\mathcal L_i,$
in such a way that
Let
![]() $\gamma \in \Gamma _i.$
By
$\gamma \in \Gamma _i.$
By
![]() $(*)$
and
$(*)$
and
![]() $(**)$
above, we have
$(**)$
above, we have
for all
![]() $g\in G.$
On the other hand, let
$g\in G.$
On the other hand, let
![]() $G_i$
be the stabilizer of
$G_i$
be the stabilizer of
![]() $\pi _i$
in
$\pi _i$
in
![]() $\mathrm {Aut}(G)\ltimes G$
; then
$\mathrm {Aut}(G)\ltimes G$
; then
![]() $\pi _i$
extends to an irreducible projective representation
$\pi _i$
extends to an irreducible projective representation
![]() $ \widetilde {\pi }_i$
of
$ \widetilde {\pi }_i$
of
![]() $G_i$
(see §2). Since
$G_i$
(see §2). Since
it follows from
![]() $(***)$
that
$(***)$
that
![]() $(\widetilde {\pi _i}(\gamma ^{-1})\otimes I_{\mathcal L_i})V_i(\gamma )$
commutes with
$(\widetilde {\pi _i}(\gamma ^{-1})\otimes I_{\mathcal L_i})V_i(\gamma )$
commutes with
![]() $\pi _i(g)\otimes I_{\mathcal L_i}$
for all
$\pi _i(g)\otimes I_{\mathcal L_i}$
for all
![]() $g\in G.$
As
$g\in G.$
As
![]() $\pi _i$
is irreducible, there exists a unitary operator
$\pi _i$
is irreducible, there exists a unitary operator
![]() $W_i(\gamma )$
on
$W_i(\gamma )$
on
![]() $\mathcal L_i$
such that
$\mathcal L_i$
such that
It is clear that
![]() $W_i$
is a projective unitary representation of
$W_i$
is a projective unitary representation of
![]() $\Gamma _i\ltimes G$
, since
$\Gamma _i\ltimes G$
, since
![]() $V_i$
is a unitary representation of
$V_i$
is a unitary representation of
![]() $\Gamma _i\ltimes G$
.
$\Gamma _i\ltimes G$
.
6 Unitary dual of solenoids
Let p be either a prime integer or
![]() $p=\infty .$
Define an element
$p=\infty .$
Define an element
![]() $e_p$
in the unitary dual group
$e_p$
in the unitary dual group
![]() $\widehat {\mathbf Q_p}$
of the additive group of
$\widehat {\mathbf Q_p}$
of the additive group of
![]() $\mathbf Q_p$
(recall that
$\mathbf Q_p$
(recall that
![]() $\mathbf Q_\infty = {\mathbf R}$
) by
$\mathbf Q_\infty = {\mathbf R}$
) by
![]() $e_p(x)= e^{2\pi i x}$
if
$e_p(x)= e^{2\pi i x}$
if
![]() $p=\infty $
and
$p=\infty $
and
![]() $e_p(x)= \exp (2\pi i \{x\})$
otherwise, where
$e_p(x)= \exp (2\pi i \{x\})$
otherwise, where
![]() $\{x\}= \sum _{j=m}^{-1} a_j p^j $
denotes the ‘fractional part’ of a p-adic number
$\{x\}= \sum _{j=m}^{-1} a_j p^j $
denotes the ‘fractional part’ of a p-adic number
![]() $x= \sum _{j=m}^\infty a_j p^j$
for integers
$x= \sum _{j=m}^\infty a_j p^j$
for integers
![]() $m\in {\mathbf Z}$
and
$m\in {\mathbf Z}$
and
![]() $a_j \in \{0, \ldots , p-1\}$
. Observe that
$a_j \in \{0, \ldots , p-1\}$
. Observe that
![]() $\mathrm {Ker} (e_p)={\mathbf Z}$
if
$\mathrm {Ker} (e_p)={\mathbf Z}$
if
![]() $p=\infty $
and that
$p=\infty $
and that
![]() $\mathrm {Ker} (e_p)={\mathbf Z}_p$
if p is a prime integer, where
$\mathrm {Ker} (e_p)={\mathbf Z}_p$
if p is a prime integer, where
![]() ${\mathbf Z}_p$
is the ring of p-adic integers. The map
${\mathbf Z}_p$
is the ring of p-adic integers. The map
is an isomorphism of topological groups (see [Reference Bekka, de la Harpe and ValetteBeHV08, §D.4]).
Fix an integer
![]() $d\geq 1.$
Then
$d\geq 1.$
Then
![]() $\widehat {\mathbf Q_p^d}$
will be identified with
$\widehat {\mathbf Q_p^d}$
will be identified with
![]() $\mathbf Q_p^d$
by means of the map
$\mathbf Q_p^d$
by means of the map
where
![]() $x\cdot y= \sum _{i=1}^d x_i y_i$
for
$x\cdot y= \sum _{i=1}^d x_i y_i$
for
![]() $x=(x_1, \ldots , x_d), y=(y_1, \ldots , y_d)\in \mathbf Q_p^d.$
$x=(x_1, \ldots , x_d), y=(y_1, \ldots , y_d)\in \mathbf Q_p^d.$
Let
![]() $S= \{p_1, \ldots , p_r, \infty \}$
, where
$S= \{p_1, \ldots , p_r, \infty \}$
, where
![]() $p_1, \ldots , p_r$
are integer primes. For an integer
$p_1, \ldots , p_r$
are integer primes. For an integer
![]() $d\geq 1$
, consider the S-adic solenoid
$d\geq 1$
, consider the S-adic solenoid
where
![]() ${\mathbf Z}[1/S]^d={\mathbf Z}[1/p_1, \ldots , 1/p_r]^d$
is embedded diagonally in
${\mathbf Z}[1/S]^d={\mathbf Z}[1/p_1, \ldots , 1/p_r]^d$
is embedded diagonally in
![]() $\mathbf Q_S= \prod _{p\in S} \mathbf Q_p.$
Then
$\mathbf Q_S= \prod _{p\in S} \mathbf Q_p.$
Then
![]() $\widehat {\mathbf {Sol}_S}$
is identified with the annihilator of
$\widehat {\mathbf {Sol}_S}$
is identified with the annihilator of
![]() ${\mathbf Z}[1/S]^d$
in
${\mathbf Z}[1/S]^d$
in
![]() $\mathbf Q_S^d,$
that is, with
$\mathbf Q_S^d,$
that is, with
![]() ${\mathbf Z}[1/S]^d$
embedded in
${\mathbf Z}[1/S]^d$
embedded in
![]() $\mathbf Q_S^d$
via the map
$\mathbf Q_S^d$
via the map
Under this identification, the dual action of the automorphism group
on
![]() $\widehat {\mathbf Q_S^d}$
corresponds to the right action on
$\widehat {\mathbf Q_S^d}$
corresponds to the right action on
![]() ${\mathbf R}^d\times \mathbf Q_{p_1}^d\times \cdots \times \mathbf Q_{p_r}^d$
given by
${\mathbf R}^d\times \mathbf Q_{p_1}^d\times \cdots \times \mathbf Q_{p_r}^d$
given by
where
![]() $(g,a)\mapsto ga$
is the usual (left) linear action of
$(g,a)\mapsto ga$
is the usual (left) linear action of
![]() $GL_d(\mathbf {k})$
on
$GL_d(\mathbf {k})$
on
![]() $\mathbf {k}^d$
for a field
$\mathbf {k}^d$
for a field
![]() $\mathbf {k}.$
$\mathbf {k}.$
7 Unitary representations of unipotent groups
Let
![]() $\mathbf {U}$
be a linear algebraic unipotent group defined over
$\mathbf {U}$
be a linear algebraic unipotent group defined over
![]() $\mathbf Q$
. The Lie algebra
$\mathbf Q$
. The Lie algebra
![]() $\mathfrak {u}$
is defined over
$\mathfrak {u}$
is defined over
![]() $\mathbf Q$
and the exponential map
$\mathbf Q$
and the exponential map
![]() $\exp : \mathfrak {u}\to U$
is a bijective morphism of algebraic varieties.
$\exp : \mathfrak {u}\to U$
is a bijective morphism of algebraic varieties.
Let p be either a prime integer or
![]() $p=\infty .$
The irreducible unitary representations of
$p=\infty .$
The irreducible unitary representations of
![]() $U_p:=\mathbf {U}(\mathbf Q_p)$
are parametrized by Kirillov’s theory as follows.
$U_p:=\mathbf {U}(\mathbf Q_p)$
are parametrized by Kirillov’s theory as follows.
The Lie algebra of
![]() $U_p$
is
$U_p$
is
![]() $\mathfrak {u}_p=\mathfrak {u}(\mathbf Q)\otimes _{\mathbf Q} \mathbf {Q}_p,$
where
$\mathfrak {u}_p=\mathfrak {u}(\mathbf Q)\otimes _{\mathbf Q} \mathbf {Q}_p,$
where
![]() $\mathfrak {u}(\mathbf Q)$
is the Lie algebra over
$\mathfrak {u}(\mathbf Q)$
is the Lie algebra over
![]() $\mathbf Q$
consisting of the
$\mathbf Q$
consisting of the
![]() $\mathbf Q$
-points in
$\mathbf Q$
-points in
![]() $\mathfrak u.$
$\mathfrak u.$
Fix an element f in the dual space
![]() ${\mathfrak u}_p^*= {\mathcal Hom}_{\mathbf Q_p}({\mathfrak u}_p, \mathbf Q_p)$
of
${\mathfrak u}_p^*= {\mathcal Hom}_{\mathbf Q_p}({\mathfrak u}_p, \mathbf Q_p)$
of
![]() $\mathfrak {u}_p.$
There exists a polarization
$\mathfrak {u}_p.$
There exists a polarization
![]() $\mathfrak m$
for
$\mathfrak m$
for
![]() $f,$
that is, a Lie subalgebra
$f,$
that is, a Lie subalgebra
![]() $\mathfrak m$
of
$\mathfrak m$
of
![]() ${\mathfrak u}_p$
such that
${\mathfrak u}_p$
such that
![]() $f([{\mathfrak m},{\mathfrak m}])=0$
and which is of maximal dimension. The induced representation
$f([{\mathfrak m},{\mathfrak m}])=0$
and which is of maximal dimension. The induced representation
![]() $\mathrm {Ind}_M^{U_p} \chi _f$
is irreducible, where
$\mathrm {Ind}_M^{U_p} \chi _f$
is irreducible, where
![]() $M=\exp (\mathfrak m)$
and
$M=\exp (\mathfrak m)$
and
![]() $\chi _f$
is the unitary character of M defined by
$\chi _f$
is the unitary character of M defined by
where
![]() $e_p\in \widehat {\mathbf Q_p}$
is as in §6. The unitary equivalence class of
$e_p\in \widehat {\mathbf Q_p}$
is as in §6. The unitary equivalence class of
![]() $\mathrm {Ind}_M^{U_p} \chi _f$
only depends on the co-adjoint orbit
$\mathrm {Ind}_M^{U_p} \chi _f$
only depends on the co-adjoint orbit
![]() $\mathrm {Ad}^* (U_p) f$
of f. The resulting map
$\mathrm {Ad}^* (U_p) f$
of f. The resulting map
called the Kirillov map, from the orbit space
![]() ${\mathfrak u}_p^*/\mathrm {Ad}^*(U_p)$
of the co-adjoint representation to the unitary dual
${\mathfrak u}_p^*/\mathrm {Ad}^*(U_p)$
of the co-adjoint representation to the unitary dual
![]() $\widehat {U}_p$
of
$\widehat {U}_p$
of
![]() $U_p$
, is a bijection. In particular,
$U_p$
, is a bijection. In particular,
![]() $U_p$
is a so-called type I locally compact group. For all of this, see [Reference KirillovKiri62] or [Reference Corwin and GreenleafCoGr89] in the case of
$U_p$
is a so-called type I locally compact group. For all of this, see [Reference KirillovKiri62] or [Reference Corwin and GreenleafCoGr89] in the case of
![]() $p=\infty $
and [Reference MooreMoor65] in the case of a prime integer p.
$p=\infty $
and [Reference MooreMoor65] in the case of a prime integer p.
The group
![]() $\mathrm {Aut} (U_p)$
of continuous automorphisms of
$\mathrm {Aut} (U_p)$
of continuous automorphisms of
![]() $U_p$
can be identified with the group of
$U_p$
can be identified with the group of
![]() $\mathbf Q_p$
-points of the algebraic group
$\mathbf Q_p$
-points of the algebraic group
![]() $\mathrm {Aut} (\mathfrak u)$
of automorphisms of the Lie algebra
$\mathrm {Aut} (\mathfrak u)$
of automorphisms of the Lie algebra
![]() $\mathfrak u$
of
$\mathfrak u$
of
![]() $\mathbf {U}.$
Notice also that the natural action of
$\mathbf {U}.$
Notice also that the natural action of
![]() $\mathrm {Aut}(U_p)$
on
$\mathrm {Aut}(U_p)$
on
![]() ${\mathfrak u}_p$
as well as its dual action on
${\mathfrak u}_p$
as well as its dual action on
![]() ${\mathfrak u}_p^*$
are algebraic.
${\mathfrak u}_p^*$
are algebraic.
Let
![]() $\pi \in \widehat {U_p}$
with corresponding Kirillov orbit
$\pi \in \widehat {U_p}$
with corresponding Kirillov orbit
![]() $\mathcal {O}_\pi $
and
$\mathcal {O}_\pi $
and
![]() $g\in \mathrm {Aut}(U_p).$
Then
$g\in \mathrm {Aut}(U_p).$
Then
![]() $g(\mathcal {O}_\pi )$
is the Kirillov orbit associated to the conjugate representation
$g(\mathcal {O}_\pi )$
is the Kirillov orbit associated to the conjugate representation
![]() $\pi ^g.$
$\pi ^g.$
Lemma 10. Let
![]() $\pi $
be an irreducible unitary representation of
$\pi $
be an irreducible unitary representation of
![]() $U_p.$
The stabilizer
$U_p.$
The stabilizer
![]() $G_\pi $
of
$G_\pi $
of
![]() $\pi $
in
$\pi $
in
![]() $\mathrm {Aut}(U_p)$
is an algebraic subgroup of
$\mathrm {Aut}(U_p)$
is an algebraic subgroup of
![]() $\mathrm {Aut}(U_p).$
$\mathrm {Aut}(U_p).$
Proof. Let
![]() ${\mathcal O}_\pi \subset {\mathfrak u}_p^*$
be the Kirillov orbit corresponding to
${\mathcal O}_\pi \subset {\mathfrak u}_p^*$
be the Kirillov orbit corresponding to
![]() $\pi .$
Then
$\pi .$
Then
![]() $G_\pi $
is the set of
$G_\pi $
is the set of
![]() $g\in \mathrm {Aut}(U_p)$
such that
$g\in \mathrm {Aut}(U_p)$
such that
![]() $g(\mathcal {O}_\pi )= \mathcal {O}_\pi .$
As
$g(\mathcal {O}_\pi )= \mathcal {O}_\pi .$
As
![]() $\mathcal {O}_\pi $
is an algebraic subvariety of
$\mathcal {O}_\pi $
is an algebraic subvariety of
![]() ${\mathfrak u}_p^*$
, the claim follows.
${\mathfrak u}_p^*$
, the claim follows.
8 Decay of matrix coefficients of unitary representations of S-adic groups
Let p be an integer prime or
![]() $p=\infty $
and let
$p=\infty $
and let
![]() $\mathbf {U}$
be a linear algebraic unipotent group defined over
$\mathbf {U}$
be a linear algebraic unipotent group defined over
![]() $\mathbf Q_p$
. Set
$\mathbf Q_p$
. Set
![]() $U_p:=\mathbf {U}(\mathbf Q_p).$
$U_p:=\mathbf {U}(\mathbf Q_p).$
Let
![]() $\pi $
be an irreducible unitary representation of
$\pi $
be an irreducible unitary representation of
![]() $U_p$
. Recall (see Lemma 10) that the stabilizer
$U_p$
. Recall (see Lemma 10) that the stabilizer
![]() $G_\pi $
of
$G_\pi $
of
![]() $\pi $
in
$\pi $
in
![]() $\mathrm {Aut}(U_p)$
is an algebraic subgroup of
$\mathrm {Aut}(U_p)$
is an algebraic subgroup of
![]() $\mathrm {Aut}(U_p).$
Recall also (see Lemma 6) that
$\mathrm {Aut}(U_p).$
Recall also (see Lemma 6) that
![]() $\pi $
extends to a projective representation of
$\pi $
extends to a projective representation of
![]() $G_\pi $
. The following result was proved in [Reference Bekka and HeuBeGu15, Proposition 22] in the case where
$G_\pi $
. The following result was proved in [Reference Bekka and HeuBeGu15, Proposition 22] in the case where
![]() $p=\infty ,$
using arguments from [Reference Howe and TanHoMo79]. The proof in the case where p is a prime integer is along similar lines and will be omitted.
$p=\infty ,$
using arguments from [Reference Howe and TanHoMo79]. The proof in the case where p is a prime integer is along similar lines and will be omitted.
Proposition 11. Let
![]() $\pi $
be an irreducible unitary representation of
$\pi $
be an irreducible unitary representation of
![]() $U_p$
and let
$U_p$
and let
![]() $\widetilde {\pi }$
be a projective unitary representation of
$\widetilde {\pi }$
be a projective unitary representation of
![]() ${G}_{\pi }$
which extends
${G}_{\pi }$
which extends
![]() ${\pi }.$
There exists a real number
${\pi }.$
There exists a real number
![]() $r\geq 1,$
only depending on the dimension of
$r\geq 1,$
only depending on the dimension of
![]() $G_\pi ,$
such that
$G_\pi ,$
such that
![]() $\widetilde {\pi }$
is strongly
$\widetilde {\pi }$
is strongly
![]() $L^r$
modulo its projective kernel.
$L^r$
modulo its projective kernel.
We will need later a precise description of the projective kernel of a representation
![]() $\widetilde {\pi }$
as above.
$\widetilde {\pi }$
as above.
Lemma 12. Let
![]() $\pi $
be an irreducible unitary representation of
$\pi $
be an irreducible unitary representation of
![]() $U_p$
and
$U_p$
and
![]() $\widetilde {\pi }$
a projective unitary representation of
$\widetilde {\pi }$
a projective unitary representation of
![]() ${G}_{\pi }$
which extends
${G}_{\pi }$
which extends
![]() ${\pi }.$
Let
${\pi }.$
Let
![]() ${\mathcal O}_\pi \subset {\mathfrak u}_p^*$
be the corresponding Kirillov orbit of
${\mathcal O}_\pi \subset {\mathfrak u}_p^*$
be the corresponding Kirillov orbit of
![]() $\pi .$
For
$\pi .$
For
![]() $g\in \mathrm {Aut}(U_p),$
the following properties are equivalent.
$g\in \mathrm {Aut}(U_p),$
the following properties are equivalent.
-
(i) g belongs to the projective kernel
 $P_{\widetilde {\pi }}$
of
$P_{\widetilde {\pi }}$
of
 $\widetilde {\pi }$
.
$\widetilde {\pi }$
. -
(ii) For every
 $u\in U_p$
, we have
$u\in U_p$
, we have  $$ \begin{align*}g(u)u^{-1}\in \bigcap_{f\in {\mathcal O}_\pi}\exp (\mathrm{ Ker}(f)).\end{align*} $$
$$ \begin{align*}g(u)u^{-1}\in \bigcap_{f\in {\mathcal O}_\pi}\exp (\mathrm{ Ker}(f)).\end{align*} $$
Proof. We can assume that
![]() $\pi = \mathrm {Ind}_M^{U_p} \chi _{f_0}$
, for
$\pi = \mathrm {Ind}_M^{U_p} \chi _{f_0}$
, for
![]() $f_0\in {\mathcal O}_\pi ,$
and
$f_0\in {\mathcal O}_\pi ,$
and
![]() $M= \exp \mathfrak m$
for a polarization
$M= \exp \mathfrak m$
for a polarization
![]() $\mathfrak m$
of
$\mathfrak m$
of
![]() $f_0$
.
$f_0$
.
Let
![]() $g\in \mathrm {Aut}(U_p).$
If g is in the stabilizer
$g\in \mathrm {Aut}(U_p).$
If g is in the stabilizer
![]() $G_\pi $
of
$G_\pi $
of
![]() $\pi $
in
$\pi $
in
![]() $\mathrm {Aut}(U_p)$
, recall (see Proof of Lemma 6) that
$\mathrm {Aut}(U_p)$
, recall (see Proof of Lemma 6) that
Since
![]() $\pi $
is irreducible, it follows from Schur’s lemma that
$\pi $
is irreducible, it follows from Schur’s lemma that
![]() $g\in P_{\widetilde {\pi }}$
if and only if
$g\in P_{\widetilde {\pi }}$
if and only if
that is,
Now we have (see [Reference Bekka and HeuBeGu15, Lemma 18])
 $$ \begin{align*}\mathrm{Ker} (\pi) =\bigcap_{f\in {\mathcal O}_\pi} \mathrm{Ker} (\chi_{f}\!),\end{align*} $$
$$ \begin{align*}\mathrm{Ker} (\pi) =\bigcap_{f\in {\mathcal O}_\pi} \mathrm{Ker} (\chi_{f}\!),\end{align*} $$
and so
![]() $g\in P_{\widetilde {\pi }}$
if and only if
$g\in P_{\widetilde {\pi }}$
if and only if
 $$ \begin{align*}g(u)u^{-1}\in \bigcap_{f\in {\mathcal O}_\pi} \mathrm{Ker} (\chi_{f}\!) \quad\text{for all } u\in U_p.\end{align*} $$
$$ \begin{align*}g(u)u^{-1}\in \bigcap_{f\in {\mathcal O}_\pi} \mathrm{Ker} (\chi_{f}\!) \quad\text{for all } u\in U_p.\end{align*} $$
Let
![]() $g\in P_{\widetilde {\pi }}.$
Denote by
$g\in P_{\widetilde {\pi }}.$
Denote by
![]() $X\mapsto g(X)$
the automorphism of
$X\mapsto g(X)$
the automorphism of
![]() $\mathfrak {u}_p$
corresponding to
$\mathfrak {u}_p$
corresponding to
![]() $g.$
Let
$g.$
Let
![]() $u=\exp (X)$
for
$u=\exp (X)$
for
![]() $X\in \mathfrak {u}_p$
and
$X\in \mathfrak {u}_p$
and
![]() $f\in {\mathcal O}_\pi $
. Set
$f\in {\mathcal O}_\pi $
. Set
![]() $u_t= \exp (tX).$
By the Campbell Hausdorff formula, there exist
$u_t= \exp (tX).$
By the Campbell Hausdorff formula, there exist
![]() $Y_1, \ldots Y_r\in \mathfrak {u}_p$
such that
$Y_1, \ldots Y_r\in \mathfrak {u}_p$
such that
for every
![]() $t\in \mathbf Q_p$
. Since
$t\in \mathbf Q_p$
. Since
it follows that the polynomial
takes its values in
![]() ${\mathbf Z}$
if
${\mathbf Z}$
if
![]() $p=\infty $
, and in
$p=\infty $
, and in
![]() ${\mathbf Z}_p$
(and so Q has bounded image) otherwise. This clearly implies that
${\mathbf Z}_p$
(and so Q has bounded image) otherwise. This clearly implies that
![]() $Q(t)=0$
for all
$Q(t)=0$
for all
![]() $t\in \mathbf Q_p$
; in particular, we have
$t\in \mathbf Q_p$
; in particular, we have
This shows that (i) implies (ii).
Conversely, assume that (ii) holds. Then clearly
 $$ \begin{align*}g(u)u^{-1}\in \bigcap_{f\in {\mathcal O}_\pi} \mathrm{Ker} (\chi_{f}\!) \quad\text{for all } u\in U_p\end{align*} $$
$$ \begin{align*}g(u)u^{-1}\in \bigcap_{f\in {\mathcal O}_\pi} \mathrm{Ker} (\chi_{f}\!) \quad\text{for all } u\in U_p\end{align*} $$
and so
![]() $g\in P_{\widetilde {\pi }}$
.
$g\in P_{\widetilde {\pi }}$
.
9 Decomposition of the Koopman representation for a nilmanifold
Let
![]() $\mathbf {U}$
be a linear algebraic unipotent group defined over
$\mathbf {U}$
be a linear algebraic unipotent group defined over
![]() $\mathbf Q$
. Let
$\mathbf Q$
. Let
![]() $S= \{p_1, \ldots , p_r, \infty \}$
, where
$S= \{p_1, \ldots , p_r, \infty \}$
, where
![]() $p_1, \ldots , p_r$
are integer primes. Set
$p_1, \ldots , p_r$
are integer primes. Set
 $$ \begin{align*}U:=\mathbf{U}(\mathbf Q_S)=\prod_{p\in S} U_p.\end{align*} $$
$$ \begin{align*}U:=\mathbf{U}(\mathbf Q_S)=\prod_{p\in S} U_p.\end{align*} $$
Since U is a type I group, the unitary dual
![]() $\widehat U$
of U can be identified with the cartesian product
$\widehat U$
of U can be identified with the cartesian product
![]() $\prod _{p\in S} \widehat {U_p}$
via the map
$\prod _{p\in S} \widehat {U_p}$
via the map
 $$ \begin{align*} \prod_{p\in S} \widehat{U_p}\to \widehat U, \quad (\pi_p)_{p\in S} \mapsto\bigotimes_{p\in S} \pi_p, \end{align*} $$
$$ \begin{align*} \prod_{p\in S} \widehat{U_p}\to \widehat U, \quad (\pi_p)_{p\in S} \mapsto\bigotimes_{p\in S} \pi_p, \end{align*} $$
where
![]() $\bigotimes _{p\in S} \pi _p= \pi _{\infty }\otimes \pi _{p_1} \otimes \cdots \otimes \pi_{p_r}$
is the tensor product of the
$\bigotimes _{p\in S} \pi _p= \pi _{\infty }\otimes \pi _{p_1} \otimes \cdots \otimes \pi_{p_r}$
is the tensor product of the
![]() $\pi _p$
.
$\pi _p$
.
Let
![]() $\Lambda :=\mathbf {U}({\mathbf Z}[1/S])$
and consider the corresponding S-adic compact nilmanifold
$\Lambda :=\mathbf {U}({\mathbf Z}[1/S])$
and consider the corresponding S-adic compact nilmanifold
equipped with the unique U-invariant probability measure
![]() $\mu $
on its Borel subsets.
$\mu $
on its Borel subsets.
The associated S-adic solenoid is
where
![]() $\overline {U}:=U/[U,U]$
is the quotient of U by its closed commutator subgroup
$\overline {U}:=U/[U,U]$
is the quotient of U by its closed commutator subgroup
![]() $[U,U]$
and where
$[U,U]$
and where
![]() $\overline {\Lambda }$
is the image of
$\overline {\Lambda }$
is the image of
![]() $\mathbf {U}({\mathbf Z}[1/S])$
in
$\mathbf {U}({\mathbf Z}[1/S])$
in
![]() $\overline {U}.$
$\overline {U}.$
Set
 $$ \begin{align*}\mathrm{Aut}(U):=\prod_{p\in S} \mathrm{Aut}(\mathbf{U}( \mathbf Q_p))\end{align*} $$
$$ \begin{align*}\mathrm{Aut}(U):=\prod_{p\in S} \mathrm{Aut}(\mathbf{U}( \mathbf Q_p))\end{align*} $$
and denote by
![]() $\mathrm {Aut} (\mathbf {Nil}_S)$
the subgroup of all
$\mathrm {Aut} (\mathbf {Nil}_S)$
the subgroup of all
![]() $g\in \mathrm {Aut}(U)$
with
$g\in \mathrm {Aut}(U)$
with
![]() $g(\Lambda ) =\Lambda .$
Observe that
$g(\Lambda ) =\Lambda .$
Observe that
![]() $\mathrm {Aut}(\mathbf {Nil}_S)$
is a discrete subgroup of
$\mathrm {Aut}(\mathbf {Nil}_S)$
is a discrete subgroup of
![]() $\mathrm { Aut}(U)$
, where every
$\mathrm { Aut}(U)$
, where every
![]() $\mathrm {Aut}(U_p)$
is endowed with its natural (locally compact) topology and
$\mathrm {Aut}(U_p)$
is endowed with its natural (locally compact) topology and
![]() $\mathrm {Aut}(U)$
with the product topology.
$\mathrm {Aut}(U)$
with the product topology.
Let
![]() $\Gamma $
be a subgroup of
$\Gamma $
be a subgroup of
![]() $\mathrm {Aut} (\mathbf {Nil}_S)$
. Let
$\mathrm {Aut} (\mathbf {Nil}_S)$
. Let
![]() $\kappa $
be the Koopman representation of
$\kappa $
be the Koopman representation of
![]() $\Gamma \ltimes U$
on
$\Gamma \ltimes U$
on
![]() $L^2(\mathbf {Nil}_S)$
associated to the action
$L^2(\mathbf {Nil}_S)$
associated to the action
![]() $\Gamma \ltimes U\curvearrowright \mathbf {Nil}_S.$
By Proposition 9, there exists a family
$\Gamma \ltimes U\curvearrowright \mathbf {Nil}_S.$
By Proposition 9, there exists a family
![]() $(\pi _i)_{i\in I}$
of irreducible representations of
$(\pi _i)_{i\in I}$
of irreducible representations of
![]() $U,$
such that
$U,$
such that
![]() $\kappa $
is equivalent to
$\kappa $
is equivalent to
where
![]() $ \widetilde {\pi }_i$
is an irreducible projective representation
$ \widetilde {\pi }_i$
is an irreducible projective representation
![]() $ \widetilde {\pi }_i$
of the stabilizer
$ \widetilde {\pi }_i$
of the stabilizer
![]() $G_i$
of
$G_i$
of
![]() $\pi _i$
in
$\pi _i$
in
![]() $\mathrm {Aut}(U)\ltimes U$
extending
$\mathrm {Aut}(U)\ltimes U$
extending
![]() $\pi _i$
, and where
$\pi _i$
, and where
![]() $W_i$
is a projective unitary representation of
$W_i$
is a projective unitary representation of
![]() $G_i \cap (\Gamma \ltimes U)$
.
$G_i \cap (\Gamma \ltimes U)$
.
Fix
![]() $i\in I.$
We have
$i\in I.$
We have
![]() $\pi _i=\bigotimes _{p\in S}\pi _{i,p}$
for irreducible representations
$\pi _i=\bigotimes _{p\in S}\pi _{i,p}$
for irreducible representations
![]() $\pi _{i, p}$
of
$\pi _{i, p}$
of
![]() $U_p.$
$U_p.$
We will need the following more precise description of
![]() $\pi _i.$
Recall that
$\pi _i.$
Recall that
![]() $\mathfrak u$
is the Lie algebra of
$\mathfrak u$
is the Lie algebra of
![]() $\mathbf U$
and that
$\mathbf U$
and that
![]() $\mathfrak {u}(\mathbf Q)$
denotes the Lie algebra over
$\mathfrak {u}(\mathbf Q)$
denotes the Lie algebra over
![]() $\mathbf Q$
consisting of the
$\mathbf Q$
consisting of the
![]() $\mathbf Q$
-points in
$\mathbf Q$
-points in
![]() $\mathfrak u.$
$\mathfrak u.$
Let
![]() $\mathfrak {u}^*(\mathbf Q)$
be the set of
$\mathfrak {u}^*(\mathbf Q)$
be the set of
![]() $\mathbf Q$
-rational points in the dual space
$\mathbf Q$
-rational points in the dual space
![]() $\mathfrak u^*$
; so,
$\mathfrak u^*$
; so,
![]() $\mathfrak {u}^*(\mathbf Q)$
is the subspace of
$\mathfrak {u}^*(\mathbf Q)$
is the subspace of
![]() $f\in \mathfrak u^*$
with
$f\in \mathfrak u^*$
with
![]() $f(X)\in \mathbf Q$
for all
$f(X)\in \mathbf Q$
for all
![]() $X\in \mathfrak {u}(\mathbf Q).$
Observe that, for
$X\in \mathfrak {u}(\mathbf Q).$
Observe that, for
![]() $f\in \mathfrak {u}^*(\mathbf Q),$
we have
$f\in \mathfrak {u}^*(\mathbf Q),$
we have
![]() $f(X)\in \mathbf Q_p$
for all
$f(X)\in \mathbf Q_p$
for all
![]() $X\in \mathfrak {u}_p=\mathfrak {u}(\mathbf Q_p)$
.
$X\in \mathfrak {u}_p=\mathfrak {u}(\mathbf Q_p)$
.
A polarization for
![]() $f\in \mathfrak {u}^*(\mathbf Q)$
is a Lie subalgebra
$f\in \mathfrak {u}^*(\mathbf Q)$
is a Lie subalgebra
![]() $\mathfrak m$
of
$\mathfrak m$
of
![]() ${\mathfrak u}(\mathbf Q)$
such that
${\mathfrak u}(\mathbf Q)$
such that
![]() $f([{\mathfrak m},{\mathfrak m}])=0$
and which is of maximal dimension with this property.
$f([{\mathfrak m},{\mathfrak m}])=0$
and which is of maximal dimension with this property.
Proposition 13. Let
![]() $\pi _i= \bigotimes _{p\in S} \pi _{i, p}$
be one of the irreducible representations of
$\pi _i= \bigotimes _{p\in S} \pi _{i, p}$
be one of the irreducible representations of
![]() $U=\mathbf {U}(\mathbf Q_S)$
appearing in the decomposition
$U=\mathbf {U}(\mathbf Q_S)$
appearing in the decomposition
![]() $L^2(\mathbf {Nil}_S)$
as above. There exist
$L^2(\mathbf {Nil}_S)$
as above. There exist
![]() $f_i\in \mathfrak {u}^*(\mathbf Q)$
and a polarization
$f_i\in \mathfrak {u}^*(\mathbf Q)$
and a polarization
![]() $\mathfrak {m}_{i} \subset \mathfrak {u}(\mathbf Q)$
for
$\mathfrak {m}_{i} \subset \mathfrak {u}(\mathbf Q)$
for
![]() $f_i$
with the following property: for every
$f_i$
with the following property: for every
![]() $p\in S,$
the representation
$p\in S,$
the representation
![]() $\pi _{i,p}$
is equivalent to
$\pi _{i,p}$
is equivalent to
![]() $\mathrm {Ind}_{ M_{i,p}}^U \chi _{f_i},$
where:
$\mathrm {Ind}_{ M_{i,p}}^U \chi _{f_i},$
where:
-
•
 $M_{i,p}=\exp (\mathfrak {m}_{i,p})$
for
$M_{i,p}=\exp (\mathfrak {m}_{i,p})$
for
 ;
; -
•
 $\chi _{f_i}$
is the unitary character of
$\chi _{f_i}$
is the unitary character of
 $M_{i,p}$
given by
$M_{i,p}$
given by
 $\chi _{f_i}(\exp X)=e_p( f_i(X)),$
for all
$\chi _{f_i}(\exp X)=e_p( f_i(X)),$
for all
 $X \in {\mathfrak m}_{i,p},$
with
$X \in {\mathfrak m}_{i,p},$
with
 $e_p\in \widehat {\mathbf Q_p}$
as in §6.
$e_p\in \widehat {\mathbf Q_p}$
as in §6.
Proof. The same result is proved in [Reference MooreMoor65, Theorem 11] (see also [Reference FoxFox89, Theorem 1.2]) for the Koopman representation of
![]() $\mathbf {U}(\mathbf {A})$
in
$\mathbf {U}(\mathbf {A})$
in
![]() $L^2(\mathbf {U}(\mathbf {A})/ \mathbf {U}(\mathbf {Q})),$
where
$L^2(\mathbf {U}(\mathbf {A})/ \mathbf {U}(\mathbf {Q})),$
where
![]() $\mathbf {A}$
is the ring of adeles of
$\mathbf {A}$
is the ring of adeles of
![]() $\mathbf Q.$
We could check that the proof, which proceeds by induction of the dimension of
$\mathbf Q.$
We could check that the proof, which proceeds by induction of the dimension of
![]() $\mathbf {U}$
, carries over to the Koopman representation on
$\mathbf {U}$
, carries over to the Koopman representation on
![]() $L^2(\mathbf {U}(\mathbf Q_S)/ \mathbf {U}(\mathbf {{\mathbf Z}}[1/S]))$
, with the appropriate changes. We prefer to deduce our claim from the result for
$L^2(\mathbf {U}(\mathbf Q_S)/ \mathbf {U}(\mathbf {{\mathbf Z}}[1/S]))$
, with the appropriate changes. We prefer to deduce our claim from the result for
![]() $\mathbf {U}(\mathbf {A})$
, as follows.
$\mathbf {U}(\mathbf {A})$
, as follows.
It is well known (see [Reference WeilWeil74]) that
 $$ \begin{align*}\mathbf A= \bigg(\mathbf Q_S \times \prod_{p\notin S} {\mathbf Z}_p\bigg) +\mathbf Q\end{align*} $$
$$ \begin{align*}\mathbf A= \bigg(\mathbf Q_S \times \prod_{p\notin S} {\mathbf Z}_p\bigg) +\mathbf Q\end{align*} $$
and that
 $$ \begin{align*}\bigg(\mathbf Q_S \times \prod_{p\notin S} {\mathbf Z}_p\bigg)\cap \mathbf Q= {\mathbf Z}[1/S]. \end{align*} $$
$$ \begin{align*}\bigg(\mathbf Q_S \times \prod_{p\notin S} {\mathbf Z}_p\bigg)\cap \mathbf Q= {\mathbf Z}[1/S]. \end{align*} $$
This gives rise to a well-defined projection
![]() $\varphi :\mathbf {A}/ \mathbf {Q} \to \mathbf Q_S/{\mathbf Z}[1/S]$
given by
$\varphi :\mathbf {A}/ \mathbf {Q} \to \mathbf Q_S/{\mathbf Z}[1/S]$
given by
 $$ \begin{align*}\varphi((a_S, (a_p)_{p\notin S}) +\mathbf Q)= a_S+{\mathbf Z}[1/S] \quad\text{for all } a_S\in \mathbf Q_S, (a_p)_{p\notin S}\in \prod_{p\notin S} {\mathbf Z}_p;\end{align*} $$
$$ \begin{align*}\varphi((a_S, (a_p)_{p\notin S}) +\mathbf Q)= a_S+{\mathbf Z}[1/S] \quad\text{for all } a_S\in \mathbf Q_S, (a_p)_{p\notin S}\in \prod_{p\notin S} {\mathbf Z}_p;\end{align*} $$
so the fiber over a point
![]() $a_S+{\mathbf Z}[1/S]\in \mathbf Q_S/{\mathbf Z}[1/S]$
is
$a_S+{\mathbf Z}[1/S]\in \mathbf Q_S/{\mathbf Z}[1/S]$
is
This induces an identification of
![]() $\mathbf {U}(\mathbf {\mathbf Q_S})/ \mathbf {U}(\mathbf {{\mathbf Z}}[1/S])=\mathbf {Nil}_S$
with the double coset space
$\mathbf {U}(\mathbf {\mathbf Q_S})/ \mathbf {U}(\mathbf {{\mathbf Z}}[1/S])=\mathbf {Nil}_S$
with the double coset space
![]() $K_S\backslash \mathbf {U}(\mathbf {A})/ \mathbf {U}(\mathbf {Q}),$
where
$K_S\backslash \mathbf {U}(\mathbf {A})/ \mathbf {U}(\mathbf {Q}),$
where
![]() $K_S$
is the compact subgroup
$K_S$
is the compact subgroup
 $$ \begin{align*}K_S=\prod_{p\notin S}\mathbf{U}({\mathbf Z}_p)\end{align*} $$
$$ \begin{align*}K_S=\prod_{p\notin S}\mathbf{U}({\mathbf Z}_p)\end{align*} $$
of
![]() $\mathbf {U}(\mathbf {A}).$
Observe that this identification is equivariant under translation by elements from
$\mathbf {U}(\mathbf {A}).$
Observe that this identification is equivariant under translation by elements from
![]() $\mathbf {U}(\mathbf Q_S).$
In this way, we can view
$\mathbf {U}(\mathbf Q_S).$
In this way, we can view
![]() $L^2(\mathbf {Nil}_S)$
as the
$L^2(\mathbf {Nil}_S)$
as the
![]() $\mathbf {U}(\mathbf Q_S)$
-invariant subspace
$\mathbf {U}(\mathbf Q_S)$
-invariant subspace
![]() $L^2(K_S\backslash \mathbf {U}(\mathbf {A})/ \mathbf {U}(\mathbf {Q}))$
of
$L^2(K_S\backslash \mathbf {U}(\mathbf {A})/ \mathbf {U}(\mathbf {Q}))$
of
![]() $L^2(\mathbf {U}(\mathbf {A})/ \mathbf {U}(\mathbf {Q})).$
$L^2(\mathbf {U}(\mathbf {A})/ \mathbf {U}(\mathbf {Q})).$
Choose a system T of representatives for the
![]() $\mathrm {Ad}^*(\mathbf {U}(\mathbf Q))$
-orbits in
$\mathrm {Ad}^*(\mathbf {U}(\mathbf Q))$
-orbits in
![]() $ \mathfrak {u}^*(\mathbf Q)$
. By [Reference MooreMoor65, Theorem 11], for every
$ \mathfrak {u}^*(\mathbf Q)$
. By [Reference MooreMoor65, Theorem 11], for every
![]() $f\in T,$
we can find a polarization
$f\in T,$
we can find a polarization
![]() $\mathfrak {m}_{f}\subset \mathfrak {u}(\mathbf Q)$
for f with the following property: setting
$\mathfrak {m}_{f}\subset \mathfrak {u}(\mathbf Q)$
for f with the following property: setting
we have a decomposition
 $$ \begin{align*} L^2(\mathbf{U}(\mathbf{A})/ \mathbf{U}(\mathbf{Q}))= \bigoplus_{f\in T} \mathcal H_f \end{align*} $$
$$ \begin{align*} L^2(\mathbf{U}(\mathbf{A})/ \mathbf{U}(\mathbf{Q}))= \bigoplus_{f\in T} \mathcal H_f \end{align*} $$
into irreducible
![]() $\mathbf {U}(\mathbf {A})$
-invariant subspaces
$\mathbf {U}(\mathbf {A})$
-invariant subspaces
![]() $\mathcal H_f$
such that the representation
$\mathcal H_f$
such that the representation
![]() $\pi _f$
of
$\pi _f$
of
![]() $\mathbf {U}(\mathbf {A})$
in
$\mathbf {U}(\mathbf {A})$
in
![]() $\mathcal H_f$
is equivalent to
$\mathcal H_f$
is equivalent to
![]() $\mathrm {Ind}_{ M_{f}(\mathbf {A})}^{\mathbf {U}(\mathbf {A}) }\chi _{f},$
where
$\mathrm {Ind}_{ M_{f}(\mathbf {A})}^{\mathbf {U}(\mathbf {A}) }\chi _{f},$
where
and
![]() $\chi _{f, \mathbf {A}}$
is the unitary character of
$\chi _{f, \mathbf {A}}$
is the unitary character of
![]() $M_{f}(\mathbf {A})$
given by
$M_{f}(\mathbf {A})$
given by
here, e is the unitary character of
![]() $\mathbf {A}$
defined by
$\mathbf {A}$
defined by
 $$ \begin{align*} e((a_p)_p) = \prod_{p\in \mathcal P \cup \{\infty\}} e_p(a_p) \quad\text{for all } (a_p)_p\in \mathbf{A}, \end{align*} $$
$$ \begin{align*} e((a_p)_p) = \prod_{p\in \mathcal P \cup \{\infty\}} e_p(a_p) \quad\text{for all } (a_p)_p\in \mathbf{A}, \end{align*} $$
where
![]() $\mathcal P$
is the set of integer primes.
$\mathcal P$
is the set of integer primes.
We have
 $$ \begin{align*}L^2(K_S\backslash \mathbf{U}(\mathbf{A})/ \mathbf{U}(\mathbf{Q}))= \bigoplus_{f\in T} \mathcal H_f^{K_S},\end{align*} $$
$$ \begin{align*}L^2(K_S\backslash \mathbf{U}(\mathbf{A})/ \mathbf{U}(\mathbf{Q}))= \bigoplus_{f\in T} \mathcal H_f^{K_S},\end{align*} $$
where
![]() $ \mathcal H_f^{K_S}$
is the space of
$ \mathcal H_f^{K_S}$
is the space of
![]() $K_S$
-fixed vectors in
$K_S$
-fixed vectors in
![]() $\mathcal H_f.$
It is clear that the representation of
$\mathcal H_f.$
It is clear that the representation of
![]() $\mathbf {U}(\mathbf Q_S)$
in
$\mathbf {U}(\mathbf Q_S)$
in
![]() $\mathcal H_f^{K_S}$
is equivalent to
$\mathcal H_f^{K_S}$
is equivalent to
 $$ \begin{align*}\mathrm{Ind}_{ M_{f}(\mathbf{Q}_S)}^{\mathbf{U}(\mathbf Q_S) }\bigg(\bigotimes_{p\in S}\chi_{f, p}\bigg)= \bigotimes_{p\in S}(\mathrm{Ind}_{ M_{f}({\mathbf Q_p})}^{\mathbf{U}({\mathbf Q_p}) }\chi_{f,p}),\end{align*} $$
$$ \begin{align*}\mathrm{Ind}_{ M_{f}(\mathbf{Q}_S)}^{\mathbf{U}(\mathbf Q_S) }\bigg(\bigotimes_{p\in S}\chi_{f, p}\bigg)= \bigotimes_{p\in S}(\mathrm{Ind}_{ M_{f}({\mathbf Q_p})}^{\mathbf{U}({\mathbf Q_p}) }\chi_{f,p}),\end{align*} $$
where
![]() $\chi _{f, p}$
is the unitary character of
$\chi _{f, p}$
is the unitary character of
![]() $M_{f}(\mathbf Q_p)$
given by
$M_{f}(\mathbf Q_p)$
given by
Since
![]() $ M_{f}({\mathbf Q_p})$
is a polarization for f, each of the
$ M_{f}({\mathbf Q_p})$
is a polarization for f, each of the
![]() $\mathbf {U}(\mathbf Q_p)$
-representations
$\mathbf {U}(\mathbf Q_p)$
-representations
![]() $\mathrm {Ind}_{ M_{f}(\mathbf {\mathbf Q_p})}^{\mathbf {U}(\mathbf {\mathbf Q_p}) }\chi _{f,p}$
and, hence, each of the
$\mathrm {Ind}_{ M_{f}(\mathbf {\mathbf Q_p})}^{\mathbf {U}(\mathbf {\mathbf Q_p}) }\chi _{f,p}$
and, hence, each of the
![]() $\mathbf {U}(\mathbf Q_S)$
-representations
$\mathbf {U}(\mathbf Q_S)$
-representations
 $$ \begin{align*}\mathrm{Ind}_{ M_{f}({\mathbf Q_S})}^{\mathbf{U}(\mathbf Q_S) }\bigg(\bigotimes_{p\in S}\chi_{f, p}\bigg)\end{align*} $$
$$ \begin{align*}\mathrm{Ind}_{ M_{f}({\mathbf Q_S})}^{\mathbf{U}(\mathbf Q_S) }\bigg(\bigotimes_{p\in S}\chi_{f, p}\bigg)\end{align*} $$
is irreducible. This proves the claim.
We establish another crucial fact about the representations
![]() $\pi _i$
in the following proposition.
$\pi _i$
in the following proposition.
Proposition 14. With the notation of Proposition 13, let
![]() ${\mathcal O}_{\mathbf Q}(f_i)$
be the co-adjoint orbit of
${\mathcal O}_{\mathbf Q}(f_i)$
be the co-adjoint orbit of
![]() $f_i$
under
$f_i$
under
![]() $\mathbf {U}(\mathbf Q)$
and set
$\mathbf {U}(\mathbf Q)$
and set
 $$ \begin{align*} \mathfrak{k}_{i,p}=\bigcap_{f\in {\mathcal O}_{\mathbf Q}(f_i)} \mathfrak{k}_p(f), \end{align*} $$
$$ \begin{align*} \mathfrak{k}_{i,p}=\bigcap_{f\in {\mathcal O}_{\mathbf Q}(f_i)} \mathfrak{k}_p(f), \end{align*} $$
where
![]() $\mathfrak {k}_{p}(f)$
is the kernel of f in
$\mathfrak {k}_{p}(f)$
is the kernel of f in
![]() $\mathfrak {u}_{p}.$
Let
$\mathfrak {u}_{p}.$
Let
![]() $K_{i,p}= \exp ( \mathfrak {k}_{i,p})$
and
$K_{i,p}= \exp ( \mathfrak {k}_{i,p})$
and
![]() $K_i= \prod _{p\in S} K_{i,p}.$
$K_i= \prod _{p\in S} K_{i,p}.$
-
(i)
 $K_i$
is a closed normal subgroup of U and
$K_i$
is a closed normal subgroup of U and
 $K_{i} \cap \Lambda = K_i\cap \mathbf {U}({\mathbf Z}[1/S])$
is a lattice in
$K_{i} \cap \Lambda = K_i\cap \mathbf {U}({\mathbf Z}[1/S])$
is a lattice in
 $K_i.$
$K_i.$
-
(ii) Let
 $P_{\widetilde \pi _i}$
be the projective kernel of the extension
$P_{\widetilde \pi _i}$
be the projective kernel of the extension
 $\widetilde \pi _i$
of
$\widetilde \pi _i$
of
 $\pi _i$
to the stabilizer
$\pi _i$
to the stabilizer
 $G_i$
of
$G_i$
of
 $\pi _i$
in
$\pi _i$
in
 $\mathrm {Aut}(U)\ltimes U$
. For
$\mathrm {Aut}(U)\ltimes U$
. For
 $g\in G_i$
, we have
$g\in G_i$
, we have
 $g\in P_{\widetilde \pi _i}$
if and only if
$g\in P_{\widetilde \pi _i}$
if and only if
 $g(u)\in u K_i$
for every
$g(u)\in u K_i$
for every
 $u\in U.$
$u\in U.$
Proof. (i) Let
 $$ \begin{align*} \mathfrak{k}_{i,\mathbf Q}=\bigcap_{f\in {\mathcal O}_{\mathbf Q}(f_i)} \mathfrak{k}_{\mathbf Q(f)}, \end{align*} $$
$$ \begin{align*} \mathfrak{k}_{i,\mathbf Q}=\bigcap_{f\in {\mathcal O}_{\mathbf Q}(f_i)} \mathfrak{k}_{\mathbf Q(f)}, \end{align*} $$
where
![]() $\mathfrak {k}_{\mathbf Q}(f)$
is the kernel of f in
$\mathfrak {k}_{\mathbf Q}(f)$
is the kernel of f in
![]() $\mathfrak {u}(\mathbf Q).$
Observe that
$\mathfrak {u}(\mathbf Q).$
Observe that
![]() $ \mathfrak {k}_{i,\mathbf Q}$
is an ideal in
$ \mathfrak {k}_{i,\mathbf Q}$
is an ideal in
![]() $\mathfrak {u}(\mathbf Q),$
since it is
$\mathfrak {u}(\mathbf Q),$
since it is
![]() $\mathrm {Ad}(\mathbf {U}(\mathbf Q))$
-invariant. So, we have
$\mathrm {Ad}(\mathbf {U}(\mathbf Q))$
-invariant. So, we have
for an ideal
![]() $\mathfrak {k}_{i}$
in
$\mathfrak {k}_{i}$
in
![]() $ \mathfrak {u}.$
Since
$ \mathfrak {u}.$
Since
![]() $f\in \mathfrak {u}^*(\mathbf Q)$
for
$f\in \mathfrak {u}^*(\mathbf Q)$
for
![]() $f\in {\mathcal O}_{\mathbf Q}(f_i),$
we have
$f\in {\mathcal O}_{\mathbf Q}(f_i),$
we have
and hence
Let
![]() $\mathbf {K}_i=\exp ( \mathfrak {k}_{i}).$
Then
$\mathbf {K}_i=\exp ( \mathfrak {k}_{i}).$
Then
![]() $\mathbf {K}_i$
is a normal algebraic
$\mathbf {K}_i$
is a normal algebraic
![]() $\mathbf Q$
-subgroup of
$\mathbf Q$
-subgroup of
![]() $\mathbf {U}$
and we have
$\mathbf {U}$
and we have
![]() $K_{i,p}= \mathbf {K}_i(\mathbf Q_p)$
for every p; so,
$K_{i,p}= \mathbf {K}_i(\mathbf Q_p)$
for every p; so,
and
![]() $K_i \cap \Lambda = \mathbf {K}_i({\mathbf Z}[1/S])$
is a lattice in
$K_i \cap \Lambda = \mathbf {K}_i({\mathbf Z}[1/S])$
is a lattice in
![]() $K_i.$
This proves (i).
$K_i.$
This proves (i).
To prove (ii), observe that
 $$ \begin{align*}P_{\widetilde\pi_i}= \prod_{p\in S} P_{i,p},\end{align*} $$
$$ \begin{align*}P_{\widetilde\pi_i}= \prod_{p\in S} P_{i,p},\end{align*} $$
where
![]() $P_{i,p}$
is the projective kernel of
$P_{i,p}$
is the projective kernel of
![]() $\widetilde {\pi _{i,p}}$
.
$\widetilde {\pi _{i,p}}$
.
Fix
![]() $p\in S$
and let
$p\in S$
and let
![]() $g\in G_i$
. By Lemma 12,
$g\in G_i$
. By Lemma 12,
![]() $g\in P_{i,p}$
if and only if
$g\in P_{i,p}$
if and only if
![]() $g(u)\in u K_{i,p}$
for every
$g(u)\in u K_{i,p}$
for every
![]() $u\in U_p=\mathbf {U}(\mathbf Q_p). $
This finishes the proof.
$u\in U_p=\mathbf {U}(\mathbf Q_p). $
This finishes the proof.
10 Proof of Theorem 1
Let
![]() $\mathbf {U}$
be a linear algebraic unipotent group defined over
$\mathbf {U}$
be a linear algebraic unipotent group defined over
![]() $\mathbf Q$
and
$\mathbf Q$
and
![]() $S= \{p_1, \ldots , p_r, \infty \}$
, where
$S= \{p_1, \ldots , p_r, \infty \}$
, where
![]() $p_1, \ldots , p_r$
are integer primes. Set
$p_1, \ldots , p_r$
are integer primes. Set
![]() $U:=\mathbf {U}(\mathbf Q_S)$
and
$U:=\mathbf {U}(\mathbf Q_S)$
and
![]() $\Lambda :=\mathbf {U}({\mathbf Z}[1/S])$
. Let
$\Lambda :=\mathbf {U}({\mathbf Z}[1/S])$
. Let
![]() $\mathbf {Nil}_S= U/\Lambda $
and
$\mathbf {Nil}_S= U/\Lambda $
and
![]() $\mathbf {Sol}_S$
be the S-adic nilmanifold and the associated S-adic solenoid as in §9. Denote by
$\mathbf {Sol}_S$
be the S-adic nilmanifold and the associated S-adic solenoid as in §9. Denote by
![]() $\mu $
the translation-invariant probability measure on
$\mu $
the translation-invariant probability measure on
![]() $\mathbf {Nil}_S$
and let
$\mathbf {Nil}_S$
and let
![]() $\nu $
be the image of
$\nu $
be the image of
![]() $\mu $
under the canonical projection
$\mu $
under the canonical projection
![]() $\varphi : \mathbf {Nil}_S\to \mathbf {Sol}_S.$
We identify
$\varphi : \mathbf {Nil}_S\to \mathbf {Sol}_S.$
We identify
![]() $L^2(\mathbf {Sol}_S)=L^2(\mathbf {Sol}_S, \nu )$
with the closed
$L^2(\mathbf {Sol}_S)=L^2(\mathbf {Sol}_S, \nu )$
with the closed
![]() $\mathrm {Aut}(\mathbf {Nil}_S)$
-invariant subspace
$\mathrm {Aut}(\mathbf {Nil}_S)$
-invariant subspace
of
![]() $L^2(\mathbf {Nil}_S)=L^2(\mathbf {Nil}_S,\mu ).$
We have an orthogonal decomposition into
$L^2(\mathbf {Nil}_S)=L^2(\mathbf {Nil}_S,\mu ).$
We have an orthogonal decomposition into
![]() $\mathrm {Aut}(\mathbf {Nil}_S)$
-invariant subspaces
$\mathrm {Aut}(\mathbf {Nil}_S)$
-invariant subspaces
where
 $$ \begin{align*}L_0^2(\mathbf{Sol}_S)=\bigg\{f\in L^2(\mathbf{Sol}_S)\bigg| \int_{\mathbf{Nil}_S} f \,d\mu=0\bigg\}\end{align*} $$
$$ \begin{align*}L_0^2(\mathbf{Sol}_S)=\bigg\{f\in L^2(\mathbf{Sol}_S)\bigg| \int_{\mathbf{Nil}_S} f \,d\mu=0\bigg\}\end{align*} $$
and where
![]() $\mathcal H$
is the orthogonal complement of
$\mathcal H$
is the orthogonal complement of
![]() $L^2(\mathbf {Sol}_S)$
in
$L^2(\mathbf {Sol}_S)$
in
![]() $L^2(\mathbf {Nil}_S).$
$L^2(\mathbf {Nil}_S).$
Let
![]() $\Gamma $
be a subgroup of
$\Gamma $
be a subgroup of
![]() $\mathrm {Aut}(\mathbf {Nil}_S).$
Let
$\mathrm {Aut}(\mathbf {Nil}_S).$
Let
![]() $\kappa $
be the Koopman representation of
$\kappa $
be the Koopman representation of
![]() $\Gamma $
on
$\Gamma $
on
![]() $L^2(\mathbf {Nil}_S)$
and denote by
$L^2(\mathbf {Nil}_S)$
and denote by
![]() $\kappa _1$
and
$\kappa _1$
and
![]() $\kappa _2$
the restrictions of
$\kappa _2$
the restrictions of
![]() $\kappa $
to
$\kappa $
to
![]() $L_0^2(\mathbf {Sol}_S)$
and
$L_0^2(\mathbf {Sol}_S)$
and
![]() $ \mathcal H$
, respectively.
$ \mathcal H$
, respectively.
Let
![]() $\Sigma _1$
be a set of representatives for the
$\Sigma _1$
be a set of representatives for the
![]() $\Gamma $
-orbits in
$\Gamma $
-orbits in
![]() $\widehat {\mathbf {Sol}_S}\setminus \{ \mathbf {1}_{\mathbf {Sol}_S}\}$
. We have
$\widehat {\mathbf {Sol}_S}\setminus \{ \mathbf {1}_{\mathbf {Sol}_S}\}$
. We have
where
![]() $\Gamma _\chi $
is the stabilizer of
$\Gamma _\chi $
is the stabilizer of
![]() $\chi $
in
$\chi $
in
![]() $\Gamma $
and
$\Gamma $
and
![]() $\unicode{x3bb} _{\Gamma /\Gamma _\chi }$
is the quasi-regular representation of
$\unicode{x3bb} _{\Gamma /\Gamma _\chi }$
is the quasi-regular representation of
![]() $\Gamma $
on
$\Gamma $
on
![]() $\ell ^2(\Gamma /\Gamma _\chi ).$
$\ell ^2(\Gamma /\Gamma _\chi ).$
By Proposition 9, there exists a family
![]() $(\pi _i)_{i\in I}$
of irreducible representations of
$(\pi _i)_{i\in I}$
of irreducible representations of
![]() $U,$
such that
$U,$
such that
![]() $\kappa _2$
is equivalent to a direct sum
$\kappa _2$
is equivalent to a direct sum
where
![]() $\widetilde {\pi }_i$
is an irreducible projective representation of the stabilizer
$\widetilde {\pi }_i$
is an irreducible projective representation of the stabilizer
![]() $G_i$
of
$G_i$
of
![]() $\pi _i$
in
$\pi _i$
in
![]() $\mathrm {Aut}(U)$
and where
$\mathrm {Aut}(U)$
and where
![]() $W_i$
is a projective unitary representation of
$W_i$
is a projective unitary representation of
![]() $\Gamma _i := \Gamma \cap G_i.$
$\Gamma _i := \Gamma \cap G_i.$
Proposition 15. For
![]() $i\in I,$
let
$i\in I,$
let
![]() $\widetilde {\pi }_i$
be the (projective) representation of
$\widetilde {\pi }_i$
be the (projective) representation of
![]() $G_i$
and let
$G_i$
and let
![]() $\Gamma _i$
be as above. There exists a real number
$\Gamma _i$
be as above. There exists a real number
![]() $r\geq 1$
such that
$r\geq 1$
such that
![]() $\widetilde {\pi _i}|_{\Gamma _i}$
is strongly
$\widetilde {\pi _i}|_{\Gamma _i}$
is strongly
![]() $L^r$
modulo
$L^r$
modulo
![]() $ P_{\widetilde \pi _i}\cap \Gamma _i$
, where
$ P_{\widetilde \pi _i}\cap \Gamma _i$
, where
![]() $P_{\widetilde \pi _i}$
is the projective kernel of
$P_{\widetilde \pi _i}$
is the projective kernel of
![]() $\widetilde {\pi }_i.$
$\widetilde {\pi }_i.$
Proof. By Proposition 11, there exists a real number
![]() $r\geq 1$
such that the representation
$r\geq 1$
such that the representation
![]() $\widetilde {\pi }_i$
of the algebraic group
$\widetilde {\pi }_i$
of the algebraic group
![]() $G_i$
is strongly
$G_i$
is strongly
![]() $L^r$
modulo
$L^r$
modulo
![]() $P_{\widetilde \pi _i}$
. In order to show that
$P_{\widetilde \pi _i}$
. In order to show that
![]() $\widetilde {\pi _i}|_{\Gamma _i}$
is strongly
$\widetilde {\pi _i}|_{\Gamma _i}$
is strongly
![]() $L^r$
modulo
$L^r$
modulo
![]() $ P_{\widetilde \pi _i}\cap \Gamma _i$
, it suffices to show that
$ P_{\widetilde \pi _i}\cap \Gamma _i$
, it suffices to show that
![]() $\Gamma _i P_{\widetilde \pi _i}$
is closed in
$\Gamma _i P_{\widetilde \pi _i}$
is closed in
![]() $G_i$
(compare with the proof of [Reference Howe and TanHoMo79, Proposition 6.2]).
$G_i$
(compare with the proof of [Reference Howe and TanHoMo79, Proposition 6.2]).
Let
![]() $K_i$
be the closed
$K_i$
be the closed
![]() $G_i$
-invariant normal subgroup
$G_i$
-invariant normal subgroup
![]() $K_i$
of U as described in Proposition 14. Then
$K_i$
of U as described in Proposition 14. Then
![]() $\overline {\Lambda }=K_i\Lambda /K_i$
is a lattice in the unipotent group
$\overline {\Lambda }=K_i\Lambda /K_i$
is a lattice in the unipotent group
![]() $\overline {U}= U/K_i.$
By Proposition 14(ii),
$\overline {U}= U/K_i.$
By Proposition 14(ii),
![]() $P_{\widetilde \pi _i}$
coincides with the kernel of the natural homomorphism
$P_{\widetilde \pi _i}$
coincides with the kernel of the natural homomorphism
![]() $\varphi : \mathrm {Aut}(U)\to \mathrm {Aut}(\overline {U})$
. Hence, we have
$\varphi : \mathrm {Aut}(U)\to \mathrm {Aut}(\overline {U})$
. Hence, we have
Now,
![]() $\varphi (\Gamma _i)$
is a discrete (and hence closed) subgroup of
$\varphi (\Gamma _i)$
is a discrete (and hence closed) subgroup of
![]() $\mathrm {Aut}(\overline {U})$
, since
$\mathrm {Aut}(\overline {U})$
, since
![]() $\varphi (\Gamma _i)$
preserves
$\varphi (\Gamma _i)$
preserves
![]() $\overline {\Lambda }$
(and so
$\overline {\Lambda }$
(and so
![]() $\varphi ( \Gamma _i) \subset \mathrm {Aut}(\overline {U}/ \overline {\Lambda })).$
It follows from the continuity of
$\varphi ( \Gamma _i) \subset \mathrm {Aut}(\overline {U}/ \overline {\Lambda })).$
It follows from the continuity of
![]() $\varphi $
that
$\varphi $
that
![]() $\varphi ^{-1}(\varphi (\Gamma _i))$
is closed in
$\varphi ^{-1}(\varphi (\Gamma _i))$
is closed in
![]() $\mathrm {Aut}(U)$
.
$\mathrm {Aut}(U)$
.
Proof of Theorem 1
We have to show that, if
![]() $1_\Gamma $
is weakly contained in
$1_\Gamma $
is weakly contained in
![]() $\kappa _2,$
then
$\kappa _2,$
then
![]() $1_\Gamma $
is weakly contained in
$1_\Gamma $
is weakly contained in
![]() $\kappa _1.$
It suffices to show that, if
$\kappa _1.$
It suffices to show that, if
![]() $1_\Gamma $
is weakly contained in
$1_\Gamma $
is weakly contained in
![]() $\kappa _2,$
then there exists a finite-index subgroup H of
$\kappa _2,$
then there exists a finite-index subgroup H of
![]() $\Gamma $
such that
$\Gamma $
such that
![]() $1_H$
is weakly contained in
$1_H$
is weakly contained in
![]() $\kappa _1|_{H}$
(see [Reference Bekka and FranciniBeFr20, Theorem 2]).
$\kappa _1|_{H}$
(see [Reference Bekka and FranciniBeFr20, Theorem 2]).
We proceed by induction on the integer
 $$ \begin{align*}n(\Gamma):=\sum_{p\in S} \dim \mathrm{Zc}_p(\Gamma),\end{align*} $$
$$ \begin{align*}n(\Gamma):=\sum_{p\in S} \dim \mathrm{Zc}_p(\Gamma),\end{align*} $$
where
![]() $\mathrm {Zc}_p (\Gamma )$
is the Zariski closure of the projection of
$\mathrm {Zc}_p (\Gamma )$
is the Zariski closure of the projection of
![]() $\Gamma $
in
$\Gamma $
in
![]() $GL_n(\mathbf Q_p)$
.
$GL_n(\mathbf Q_p)$
.
If
![]() $n(\Gamma )=0,$
then
$n(\Gamma )=0,$
then
![]() $\Gamma $
is finite and there is nothing to prove.
$\Gamma $
is finite and there is nothing to prove.
Assume that
![]() $n(\Gamma )\geq 1$
and that the claim above is proved for every countable subgroup H of
$n(\Gamma )\geq 1$
and that the claim above is proved for every countable subgroup H of
![]() $\mathrm {Aut}(\mathbf {Nil}_S)$
with
$\mathrm {Aut}(\mathbf {Nil}_S)$
with
![]() $n(H) <n(\Gamma ).$
$n(H) <n(\Gamma ).$
Let
![]() $I_{\mathrm {fin}} \subset I$
be the set of all
$I_{\mathrm {fin}} \subset I$
be the set of all
![]() $i\in I$
such that
$i\in I$
such that
![]() $\Gamma _i=G_i\cap \Gamma $
has finite index in
$\Gamma _i=G_i\cap \Gamma $
has finite index in
![]() $\Gamma $
and set
$\Gamma $
and set
![]() $I_{\infty }=I \setminus I_{\mathrm {fin}}.$
With
$I_{\infty }=I \setminus I_{\mathrm {fin}}.$
With
![]() $V_i=\widetilde {\pi _i}|_{\Gamma _i}\otimes W_i$
, set
$V_i=\widetilde {\pi _i}|_{\Gamma _i}\otimes W_i$
, set
Two cases can occur.
First case:
![]() $1_\Gamma $
is weakly contained in
$1_\Gamma $
is weakly contained in
![]() $\kappa _2^\infty .$
Observe that
$\kappa _2^\infty .$
Observe that
![]() $n(\Gamma _i)<n(\Gamma )$
for
$n(\Gamma _i)<n(\Gamma )$
for
![]() $i\in I_{\infty }.$
Indeed, otherwise
$i\in I_{\infty }.$
Indeed, otherwise
![]() $\mathrm {Zc}_p (\Gamma _i)$
and
$\mathrm {Zc}_p (\Gamma _i)$
and
![]() $\mathrm {Zc}_p (\Gamma )$
would have the same connected component
$\mathrm {Zc}_p (\Gamma )$
would have the same connected component
![]() $C^0_p$
for every
$C^0_p$
for every
![]() $p\in S,$
since
$p\in S,$
since
![]() $\Gamma _i \subset \Gamma .$
Then
$\Gamma _i \subset \Gamma .$
Then
 $$ \begin{align*}C^0:=\prod_{p\in S} C^0_p \end{align*} $$
$$ \begin{align*}C^0:=\prod_{p\in S} C^0_p \end{align*} $$
would stabilize
![]() $\pi _i$
and
$\pi _i$
and
![]() $\Gamma \cap C^0$
would therefore be contained in
$\Gamma \cap C^0$
would therefore be contained in
![]() $\Gamma _i.$
Since
$\Gamma _i.$
Since
![]() $\Gamma \cap C^0$
has finite index in
$\Gamma \cap C^0$
has finite index in
![]() $\Gamma ,$
this would contradict the fact that
$\Gamma ,$
this would contradict the fact that
![]() $\Gamma _i$
has infinite index in
$\Gamma _i$
has infinite index in
![]() $\Gamma .$
$\Gamma .$
By restriction,
![]() $1_{\Gamma _i}$
is weakly contained in
$1_{\Gamma _i}$
is weakly contained in
![]() $\kappa _2|_{\Gamma _i}$
for every
$\kappa _2|_{\Gamma _i}$
for every
![]() $i\in I.$
Hence, by the induction hypothesis,
$i\in I.$
Hence, by the induction hypothesis,
![]() $1_{\Gamma _i}$
is weakly contained in
$1_{\Gamma _i}$
is weakly contained in
![]() $\kappa _1|_{\Gamma _i}$
for every
$\kappa _1|_{\Gamma _i}$
for every
![]() $i\in I_\infty .$
Now, on the one hand, we have
$i\in I_\infty .$
Now, on the one hand, we have

for a subset
![]() $T_i$
of
$T_i$
of
![]() $\widehat {\mathbf {Sol}_S}\setminus \{ \mathbf {1}_{\mathbf {Sol}_S}\}$
. It follows that
$\widehat {\mathbf {Sol}_S}\setminus \{ \mathbf {1}_{\mathbf {Sol}_S}\}$
. It follows that
![]() $\mathrm {Ind}_{\Gamma _i}^\Gamma 1_{\Gamma _i}=\unicode{x3bb} _{\Gamma /\Gamma _i}$
is weakly contained in
$\mathrm {Ind}_{\Gamma _i}^\Gamma 1_{\Gamma _i}=\unicode{x3bb} _{\Gamma /\Gamma _i}$
is weakly contained in

for every
![]() $i\in I_\infty .$
On the other hand, since
$i\in I_\infty .$
On the other hand, since
![]() $1_\Gamma $
is weakly contained in
$1_\Gamma $
is weakly contained in
Lemma 7 shows that
![]() $1_\Gamma $
is weakly contained in
$1_\Gamma $
is weakly contained in
![]() $\bigoplus _{i\in I_\infty }\unicode{x3bb} _{\Gamma /\Gamma _i}.$
It follows that
$\bigoplus _{i\in I_\infty }\unicode{x3bb} _{\Gamma /\Gamma _i}.$
It follows that
![]() $1_\Gamma $
is weakly contained in
$1_\Gamma $
is weakly contained in

Hence, by Lemma 7 again,
![]() $1_\Gamma $
is weakly contained in
$1_\Gamma $
is weakly contained in

This shows that
![]() $1_\Gamma $
is weakly contained in
$1_\Gamma $
is weakly contained in
![]() $\kappa _1.$
$\kappa _1.$
Second case:
![]() $1_\Gamma $
is weakly contained in
$1_\Gamma $
is weakly contained in
![]() $\kappa _2^{\mathrm {fin}}.$
By the Noetherian property of the Zariski topology, we can find finitely many indices
$\kappa _2^{\mathrm {fin}}.$
By the Noetherian property of the Zariski topology, we can find finitely many indices
![]() $i_1, \ldots , i_r$
in
$i_1, \ldots , i_r$
in
![]() $I_{\mathrm {fin}}$
such that, for every
$I_{\mathrm {fin}}$
such that, for every
![]() $p\in S,$
we have
$p\in S,$
we have
Set
![]() $H:=\Gamma _{i_1}\cap \cdots \cap \Gamma _{i_r}.$
Observe that H has finite index in
$H:=\Gamma _{i_1}\cap \cdots \cap \Gamma _{i_r}.$
Observe that H has finite index in
![]() $\Gamma .$
Moreover, it follows from Lemma 10 that
$\Gamma .$
Moreover, it follows from Lemma 10 that
![]() $\mathrm {Zc}_p(\Gamma _{i_1})\cap \cdots \cap \mathrm {Zc}_p(\Gamma _{i_r}) $
stabilizes
$\mathrm {Zc}_p(\Gamma _{i_1})\cap \cdots \cap \mathrm {Zc}_p(\Gamma _{i_r}) $
stabilizes
![]() $\pi _{i,p}$
for every
$\pi _{i,p}$
for every
![]() $i\in I_{\mathrm {fin}}$
and
$i\in I_{\mathrm {fin}}$
and
![]() $p\in S.$
Hence, H is contained in
$p\in S.$
Hence, H is contained in
![]() $\Gamma _i$
for every
$\Gamma _i$
for every
![]() $i\in I_{\mathrm {fin}}$
.
$i\in I_{\mathrm {fin}}$
.
By Proposition 9, we have a decomposition of
![]() $\kappa _2^{\mathrm { fin}}|_H$
into the direct sum
$\kappa _2^{\mathrm { fin}}|_H$
into the direct sum
By Propositions 11 and 15, there exists a real number
![]() $r\ge 1 ,$
which is independent of
$r\ge 1 ,$
which is independent of
![]() $i,$
such that
$i,$
such that
![]() $(\widetilde {\pi _i}\otimes W_i)|_H$
is a strongly
$(\widetilde {\pi _i}\otimes W_i)|_H$
is a strongly
![]() $L^r$
representation of H modulo its projective kernel
$L^r$
representation of H modulo its projective kernel
![]() $P_i$
. Observe that
$P_i$
. Observe that
![]() $P_i$
is contained in the projective kernel
$P_i$
is contained in the projective kernel
![]() $ P_{\widetilde \pi _i}$
of
$ P_{\widetilde \pi _i}$
of
![]() $ \widetilde \pi _i,$
since
$ \widetilde \pi _i,$
since
![]() $P_i= P_{\widetilde \pi _i}\cap H.$
Hence (see Proposition 8), there exists an integer
$P_i= P_{\widetilde \pi _i}\cap H.$
Hence (see Proposition 8), there exists an integer
![]() $k\geq 1$
such that
$k\geq 1$
such that
![]() $(\kappa _2^{\mathrm {fin}}|_H)^{\otimes k}$
is contained in a multiple of the direct sum
$(\kappa _2^{\mathrm {fin}}|_H)^{\otimes k}$
is contained in a multiple of the direct sum
for representations
![]() $\rho _i$
of
$\rho _i$
of
![]() $ P_i.$
Since
$ P_i.$
Since
![]() $1_H$
is weakly contained in
$1_H$
is weakly contained in
![]() $\kappa _2^{\mathrm {fin}}|H$
and hence in
$\kappa _2^{\mathrm {fin}}|H$
and hence in
![]() $(\kappa _2^{\mathrm {fin}}|_H)^{\otimes k},$
using Lemma 7, it follows that
$(\kappa _2^{\mathrm {fin}}|_H)^{\otimes k},$
using Lemma 7, it follows that
![]() $1_H$
is weakly contained in
$1_H$
is weakly contained in
Let
![]() $i\in I.$
We claim that
$i\in I.$
We claim that
![]() $P_i$
is contained in
$P_i$
is contained in
![]() $\Gamma _\chi $
for some character
$\Gamma _\chi $
for some character
![]() $\chi $
from
$\chi $
from
![]() $\widehat {\mathbf {Sol}_S}\setminus \{ \mathbf {1}_{\mathbf {Sol}_S}\}$
. Once proved, this will imply, again by Lemma 7,
$\widehat {\mathbf {Sol}_S}\setminus \{ \mathbf {1}_{\mathbf {Sol}_S}\}$
. Once proved, this will imply, again by Lemma 7,
![]() $1_H$
is weakly contained in
$1_H$
is weakly contained in
![]() $\kappa _1|_H.$
Since H has finite index in
$\kappa _1|_H.$
Since H has finite index in
![]() $\Gamma ,$
this will show that
$\Gamma ,$
this will show that
![]() $1_\Gamma $
is weakly contained in
$1_\Gamma $
is weakly contained in
![]() $\kappa _1$
and conclude the proof.
$\kappa _1$
and conclude the proof.
To prove the claim, recall from Proposition 14 that there exists a closed normal subgroup
![]() $K_i$
of U with the following properties:
$K_i$
of U with the following properties:
![]() $K_i\Lambda /K_i$
is a lattice in the unipotent algebraic group
$K_i\Lambda /K_i$
is a lattice in the unipotent algebraic group
![]() $U/K_i$
,
$U/K_i$
,
![]() $K_i$
is invariant under
$K_i$
is invariant under
![]() $ P_{\widetilde \pi _i}$
and
$ P_{\widetilde \pi _i}$
and
![]() $ P_{\widetilde \pi _i}$
acts as the identity on
$ P_{\widetilde \pi _i}$
acts as the identity on
![]() $U/K_i.$
Observe that
$U/K_i.$
Observe that
![]() $K_i\neq U$
, since
$K_i\neq U$
, since
![]() $\pi _i$
is not trivial on U. We can find a non-trivial unitary character
$\pi _i$
is not trivial on U. We can find a non-trivial unitary character
![]() $\chi $
of
$\chi $
of
![]() $U/K_i$
which is trivial on
$U/K_i$
which is trivial on
![]() $K_i\Lambda /K_i$
. Then
$K_i\Lambda /K_i$
. Then
![]() $\chi $
lifts to a non-trivial unitary character of U which is fixed by
$\chi $
lifts to a non-trivial unitary character of U which is fixed by
![]() $ P_{\widetilde \pi _i}$
and hence by
$ P_{\widetilde \pi _i}$
and hence by
![]() $P_i.$
Observe that
$P_i.$
Observe that
![]() $\chi \in \widehat {\mathbf {Sol}_S},$
since
$\chi \in \widehat {\mathbf {Sol}_S},$
since
![]() $\chi $
is trivial on
$\chi $
is trivial on
![]() $\Lambda $
.
$\Lambda $
.
11 An example: the S-adic Heisenberg nilmanifold
As an example, we study the spectral gap property for groups of automorphisms of the S-adic Heisenberg nilmanifold, proving Corollary 5. We will give a quantitative estimate for the norm of associated convolution operators, as we did in [Reference BekkaBeHe11] in the case of real Heisenberg nilmanifolds (that is, in the case
![]() $S=\{\infty \}$
).
$S=\{\infty \}$
).
Let
![]() $\mathbf K$
be an algebraically closed field containing
$\mathbf K$
be an algebraically closed field containing
![]() $\mathbf Q_p$
for
$\mathbf Q_p$
for
![]() $p=\infty $
and for all prime integers p. For an integer
$p=\infty $
and for all prime integers p. For an integer
![]() $n\geq 1$
, consider the symplectic form
$n\geq 1$
, consider the symplectic form
![]() $\beta $
on
$\beta $
on
![]() $\mathbf K^{2n}$
given by
$\mathbf K^{2n}$
given by
where J is the
![]() $(2n\times 2n)$
-matrix
$(2n\times 2n)$
-matrix
 $$ \begin{align*} J=\bigg( \begin{array}{@{}cc@{}} 0&I\\ -I_{n}& 0 \end{array}\ \bigg). \end{align*} $$
$$ \begin{align*} J=\bigg( \begin{array}{@{}cc@{}} 0&I\\ -I_{n}& 0 \end{array}\ \bigg). \end{align*} $$
The symplectic group
is an algebraic group defined over
![]() $\mathbf Q.$
$\mathbf Q.$
The
![]() $(2n+1)$
-dimensional Heisenberg group is the unipotent algebraic group
$(2n+1)$
-dimensional Heisenberg group is the unipotent algebraic group
![]() $\mathbf {H}$
defined over
$\mathbf {H}$
defined over
![]() $\mathbf Q,$
with underlying set
$\mathbf Q,$
with underlying set
![]() $\mathbf K^{2n}\times \mathbf K$
and product
$\mathbf K^{2n}\times \mathbf K$
and product
for
![]() $(x,y), (x',y')\in \mathbf K^{2n}, s,t\in \mathbf K.$
$(x,y), (x',y')\in \mathbf K^{2n}, s,t\in \mathbf K.$
The group
![]() $Sp_{2n}$
acts by rational automorphisms of
$Sp_{2n}$
acts by rational automorphisms of
![]() $\mathbf {H},$
given by
$\mathbf {H},$
given by
Let p be either an integer prime or
![]() $p=\infty .$
Set
$p=\infty .$
Set
![]() $H_p= \mathbf {H}(\mathbf Q_p).$
The center Z of
$H_p= \mathbf {H}(\mathbf Q_p).$
The center Z of
![]() $H_p$
is
$H_p$
is
![]() $\{(0,0, t)\mid t\in \mathbf Q_p\}.$
The unitary dual
$\{(0,0, t)\mid t\in \mathbf Q_p\}.$
The unitary dual
![]() $\widehat {H_p}$
of
$\widehat {H_p}$
of
![]() $H_p$
consists of the equivalence classes of the following representations:
$H_p$
consists of the equivalence classes of the following representations:
-
• the unitary characters of the abelianized group
 $H_p/Z$
;
$H_p/Z$
; -
• for every
 $t\in \mathbf Q_p\setminus \{0\},$
the infinite-dimensional representation
$t\in \mathbf Q_p\setminus \{0\},$
the infinite-dimensional representation
 $\pi _t$
defined on
$\pi _t$
defined on
 $L^2(\mathbf Q_p^n)$
by the formula for
$L^2(\mathbf Q_p^n)$
by the formula for $$ \begin{align*} \pi_t((a,b),s)\xi(x)= e_p({ts})e_p(\langle a, x-b \rangle) \xi(x-b) \end{align*} $$
$$ \begin{align*} \pi_t((a,b),s)\xi(x)= e_p({ts})e_p(\langle a, x-b \rangle) \xi(x-b) \end{align*} $$
 $((a,b),s)\in H_p, \xi \in L^2(\mathbf Q_p^n),$
and
$((a,b),s)\in H_p, \xi \in L^2(\mathbf Q_p^n),$
and
 $x\in \mathbf Q_p^n,$
where
$x\in \mathbf Q_p^n,$
where
 $e_p \in \widehat {\mathbf Q_p}$
is as in §6.
$e_p \in \widehat {\mathbf Q_p}$
is as in §6.
For
![]() $t\neq 0,$
the representation
$t\neq 0,$
the representation
![]() $\pi _t$
is, up to unitary equivalence, the unique irreducible unitary representation of
$\pi _t$
is, up to unitary equivalence, the unique irreducible unitary representation of
![]() $H_p$
whose restriction to the center Z is a multiple of the unitary character
$H_p$
whose restriction to the center Z is a multiple of the unitary character
![]() $s\mapsto e_p{(ts)}.$
$s\mapsto e_p{(ts)}.$
For
![]() $g\in Sp_{2n}(\mathbf Q_p)$
and
$g\in Sp_{2n}(\mathbf Q_p)$
and
![]() $t\in \mathbf Q_p\setminus \{0\},$
the representation
$t\in \mathbf Q_p\setminus \{0\},$
the representation
![]() $\pi _t^g$
is unitary equivalent to
$\pi _t^g$
is unitary equivalent to
![]() $\pi _t,$
since both representations have the same restriction to
$\pi _t,$
since both representations have the same restriction to
![]() $Z.$
This shows that
$Z.$
This shows that
![]() $Sp_{2n}(\mathbf Q_p)$
stabilizes
$Sp_{2n}(\mathbf Q_p)$
stabilizes
![]() $\pi _t$
. We denote the corresponding projective representation of
$\pi _t$
. We denote the corresponding projective representation of
![]() $Sp_{2n}(\mathbf Q_p)$
by
$Sp_{2n}(\mathbf Q_p)$
by
![]() $\omega _t^{(p)}$
. The representation
$\omega _t^{(p)}$
. The representation
![]() $\omega _t^{(p)}$
has different names: it is called the metaplectic representation, Weil’s representation or the oscillator representation. The projective kernel of
$\omega _t^{(p)}$
has different names: it is called the metaplectic representation, Weil’s representation or the oscillator representation. The projective kernel of
![]() $\omega _t^{(p)}$
coincides with the (finite) center of
$\omega _t^{(p)}$
coincides with the (finite) center of
![]() $Sp_{2n}(\mathbf Q_p)$
and
$Sp_{2n}(\mathbf Q_p)$
and
![]() $\omega _t^{(p)}$
is strongly
$\omega _t^{(p)}$
is strongly
![]() $L^{4n+2+ \varepsilon }$
on
$L^{4n+2+ \varepsilon }$
on
![]() $Sp_{2n}(\mathbf Q_p)$
for every
$Sp_{2n}(\mathbf Q_p)$
for every
![]() $\varepsilon>0$
(see [Reference Howe and TanHoMo79, Proposition 6.4] or [Reference Howe and MooreHowe82, Proposition 8.1]).
$\varepsilon>0$
(see [Reference Howe and TanHoMo79, Proposition 6.4] or [Reference Howe and MooreHowe82, Proposition 8.1]).
Let
![]() $S= \{p_1, \ldots , p_r, \infty \}$
, where
$S= \{p_1, \ldots , p_r, \infty \}$
, where
![]() $p_1, \ldots , p_r$
are integer primes. Set
$p_1, \ldots , p_r$
are integer primes. Set
![]() $H:=\mathbf {H}(\mathbf Q_S)$
and
$H:=\mathbf {H}(\mathbf Q_S)$
and
Let
![]() $\mathbf {Nil}_S= H/\Lambda $
; the associated S-adic solenoid is
$\mathbf {Nil}_S= H/\Lambda $
; the associated S-adic solenoid is
![]() $\mathbf {Sol}_S= \mathbf Q_S^{2n}/{\mathbf Z}[1/S]^{2n}.$
The group
$\mathbf {Sol}_S= \mathbf Q_S^{2n}/{\mathbf Z}[1/S]^{2n}.$
The group
![]() $Sp_{2n}({\mathbf Z}[1/S])$
is a subgroup of
$Sp_{2n}({\mathbf Z}[1/S])$
is a subgroup of
![]() $\mathrm { Aut}(\mathbf {Nil}_S)$
. The action of
$\mathrm { Aut}(\mathbf {Nil}_S)$
. The action of
![]() $Sp_{2n}({\mathbf Z}[1/S])$
on
$Sp_{2n}({\mathbf Z}[1/S])$
on
![]() $\mathbf {Sol}_S$
is induced by its representation by linear bijections on
$\mathbf {Sol}_S$
is induced by its representation by linear bijections on
![]() $\mathbf Q_S^{2n}$
.
$\mathbf Q_S^{2n}$
.
Let
![]() $\Gamma $
be a subgroup of
$\Gamma $
be a subgroup of
![]() $Sp_{2n}({\mathbf Z}[1/S])$
. The Koopman representation
$Sp_{2n}({\mathbf Z}[1/S])$
. The Koopman representation
![]() $\kappa $
of
$\kappa $
of
![]() $\Gamma $
on
$\Gamma $
on
![]() $L^2(\mathbf {Nil}_S)$
decomposes as
$L^2(\mathbf {Nil}_S)$
decomposes as
where
![]() $\kappa _1$
is the restriction of
$\kappa _1$
is the restriction of
![]() $\kappa $
to
$\kappa $
to
![]() $L_0^2(\mathbf {Sol}_S)$
and
$L_0^2(\mathbf {Sol}_S)$
and
![]() $\kappa _2$
the restriction of
$\kappa _2$
the restriction of
![]() $\kappa $
to the orthogonal complement of
$\kappa $
to the orthogonal complement of
![]() $L^2(\mathbf {Sol}_S)$
in
$L^2(\mathbf {Sol}_S)$
in
![]() $L^2(\mathbf {Nil}_S).$
Since
$L^2(\mathbf {Nil}_S).$
Since
![]() $Sp_{2n}(\mathbf Q_p)$
stabilizes every infinite-dimensional representation of
$Sp_{2n}(\mathbf Q_p)$
stabilizes every infinite-dimensional representation of
![]() $H_p,$
it follows from Proposition 13 that there exists a subset
$H_p,$
it follows from Proposition 13 that there exists a subset
![]() $I\subset \mathbf Q$
such that
$I\subset \mathbf Q$
such that
![]() $\kappa _2$
is equivalent to a direct sum
$\kappa _2$
is equivalent to a direct sum
 $$ \begin{align*}\bigoplus_{t\in I}\Big(\bigotimes_{p\in S}(\omega_t^{(p)}|_\Gamma\otimes W_i)\Big),\end{align*} $$
$$ \begin{align*}\bigoplus_{t\in I}\Big(\bigotimes_{p\in S}(\omega_t^{(p)}|_\Gamma\otimes W_i)\Big),\end{align*} $$
where
![]() $ W_i$
is an projective representation of
$ W_i$
is an projective representation of
![]() $\Gamma .$
$\Gamma .$
Let
![]() $\nu $
be a probability measure on
$\nu $
be a probability measure on
![]() $\Gamma .$
We can give an estimate of the norm of
$\Gamma .$
We can give an estimate of the norm of
![]() $\kappa _2(\nu )$
as in [Reference BekkaBeHe11] in the case of
$\kappa _2(\nu )$
as in [Reference BekkaBeHe11] in the case of
![]() $S=\{\infty \}.$
Indeed, by a general inequality (see [Reference Bekka and HeuBeGu15, Proposition 30]), we have
$S=\{\infty \}.$
Indeed, by a general inequality (see [Reference Bekka and HeuBeGu15, Proposition 30]), we have
for every integer
![]() $k\geq 1,$
where
$k\geq 1,$
where
![]() $\overline {\kappa _2}$
denotes the representation conjugate to
$\overline {\kappa _2}$
denotes the representation conjugate to
![]() $\kappa _2$
. Since
$\kappa _2$
. Since
![]() $\omega _t^{(p)}$
is strongly
$\omega _t^{(p)}$
is strongly
![]() $L^{4n+2+ \varepsilon }$
on
$L^{4n+2+ \varepsilon }$
on
![]() $Sp_{2n}(\mathbf Q_p)$
for any
$Sp_{2n}(\mathbf Q_p)$
for any
![]() $t\in I$
and
$t\in I$
and
![]() $p\in S,$
Proposition 8 implies that
$p\in S,$
Proposition 8 implies that
![]() $(\kappa _2\otimes \overline {\kappa _2})^{\otimes (n+1)}$
is contained in an infinite multiple of the regular representation
$(\kappa _2\otimes \overline {\kappa _2})^{\otimes (n+1)}$
is contained in an infinite multiple of the regular representation
![]() $\unicode{x3bb} _\Gamma $
of
$\unicode{x3bb} _\Gamma $
of
![]() $\Gamma .$
Hence,
$\Gamma .$
Hence,
and so,
where
![]() $\kappa _0$
is the restriction of
$\kappa _0$
is the restriction of
![]() $\kappa $
to
$\kappa $
to
![]() $L^2_0(\mathbf {Nil}_S).$
$L^2_0(\mathbf {Nil}_S).$
Assume that
![]() $\nu $
is aperiodic. If
$\nu $
is aperiodic. If
![]() $\Gamma $
is not amenable then
$\Gamma $
is not amenable then
![]() $\Vert \unicode{x3bb} _\Gamma (\nu )\Vert <1$
by Kesten’s theorem (see [Reference Bekka, de la Harpe and ValetteBeHV08, Appendix G]); so, in this case, the action of
$\Vert \unicode{x3bb} _\Gamma (\nu )\Vert <1$
by Kesten’s theorem (see [Reference Bekka, de la Harpe and ValetteBeHV08, Appendix G]); so, in this case, the action of
![]() $\Gamma $
on
$\Gamma $
on
![]() $\mathbf {Nil}_S$
has a spectral gap if and only if
$\mathbf {Nil}_S$
has a spectral gap if and only if
![]() $\Vert \kappa _1(\nu )\Vert <1,$
as stated in Theorem 1.
$\Vert \kappa _1(\nu )\Vert <1,$
as stated in Theorem 1.
Observe that, if
![]() $\Gamma $
is amenable, then the action of
$\Gamma $
is amenable, then the action of
![]() $\Gamma $
on
$\Gamma $
on
![]() $\mathbf {Nil}_S$
or
$\mathbf {Nil}_S$
or
![]() $\mathbf {Sol}_S$
does not have a spectral gap; indeed, by a general result (see [Reference del Junco and RosenblattJuRo79, Theorem 2.4]), no action of a countable amenable group by measure-preserving transformations on a non-atomic probability space has a spectral gap.
$\mathbf {Sol}_S$
does not have a spectral gap; indeed, by a general result (see [Reference del Junco and RosenblattJuRo79, Theorem 2.4]), no action of a countable amenable group by measure-preserving transformations on a non-atomic probability space has a spectral gap.
Let us look more closely to the case
![]() $n=1.$
We have
$n=1.$
We have
![]() $Sp_{2}({\mathbf Z}[1/S])=SL_2({\mathbf Z}[1/S])$
and the stabilizer of every element in
$Sp_{2}({\mathbf Z}[1/S])=SL_2({\mathbf Z}[1/S])$
and the stabilizer of every element in
![]() $\widehat {\mathbf {Sol}_S}\setminus \{ \mathbf {1}_{\mathbf {Sol}_S}\}$
is conjugate to the group of unipotent matrices in
$\widehat {\mathbf {Sol}_S}\setminus \{ \mathbf {1}_{\mathbf {Sol}_S}\}$
is conjugate to the group of unipotent matrices in
![]() $SL_2({\mathbf Z}[1/S])$
and hence amenable. This implies that
$SL_2({\mathbf Z}[1/S])$
and hence amenable. This implies that
![]() $\kappa _1$
is weakly contained in
$\kappa _1$
is weakly contained in
![]() $\unicode{x3bb} _\Gamma $
(see the decomposition of
$\unicode{x3bb} _\Gamma $
(see the decomposition of
![]() $\kappa _1$
appearing before Proposition 15); so, we have
$\kappa _1$
appearing before Proposition 15); so, we have
As a consequence, we see that the action of
![]() $\Gamma $
on
$\Gamma $
on
![]() $\mathbf {Nil}_S$
has a spectral gap if and only if
$\mathbf {Nil}_S$
has a spectral gap if and only if
![]() $\Gamma $
is not amenable.
$\Gamma $
is not amenable.