Hostname: page-component-8448b6f56d-t5pn6 Total loading time: 0 Render date: 2024-04-20T02:08:16.836Z Has data issue: false hasContentIssue false
  • English
  • Français

On the existence of homoclinic orbits on Riemannian manifolds

Published online by Cambridge University Press:  19 September 2008

Fabio Giannoni
Fabio Giannoni
Affiliation:
Center for the Mathematical Sciences, University of Wisconsin, Madison, WI53705, USA, Istituto di Matematiche Applicate ‘U.Dini’, University of Pisa, 56126 Pisa, Italy
Get access Rights & Permissions [Opens in a new window]

Abstract

We prove the existence of a non-trivial homoclinic orbit on a Riemannian manifold (possibly non-compact), for Hamiltonian systems of the second order of the form:

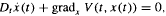
where the potential V is T-periodic in the time variable.

Type
Research Article
Information
Ergodic Theory and Dynamical Systems , Volume 14 , Issue 1 , March 1994 , pp. 103 - 127
Copyright
Copyright © Cambridge University Press 1994

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Benci, V. & Giannoni, F.. Homoclinic orbits on compact manifolds. J. Math. Anal. Appl. 157 (1991), 568–576.CrossRefGoogle Scholar
[2]Canino, A.. On p-convex sets and geodesics. J. Diff. Eq. 75 (1988), 118–157.CrossRefGoogle Scholar
[3]Coti-Zelati, V., Ekeland, I. & Séré, E.. A variational approach to homoclinic orbits in Hamiltonian systems. Math. Ann. 288 (1990), 133–160.CrossRefGoogle Scholar
[4]Coti-Zelati, V. & Rabinowitz, P. H.. Homoclinic orbits for second order Hamiltonian systems possessing superquadratic potentials. J. Amer. Math. Soc. 4 (1991), 693–727.CrossRefGoogle Scholar
[5]Fadell, E. & Husseini, S.. Category of loop space of open subsets in Euclidean space. Nonlin. Anal. T.M.A. 17 (1991), 1163–1175.CrossRefGoogle Scholar
[6]Giannoni, F.. Multiplicity of principal bounce trajectories on Riemannian manifolds. Diff. and Int. Eq. 6 (1993), 1451–1480.Google Scholar
[7]Giannoni, F. & Rabinowitz, P. H.. On the multiplicity of homoclinic orbits on Riemannian manifolds for a class of second order Hamiltonian systems. Nonl. Diff. Eq. Appl. 1 (1994), 1–46.CrossRefGoogle Scholar
[8]Hofer, H. & Wysocki, K.. First order elliptic systems and the existence of homoclinic orbits in Hamiltonian systems. Math. Ann. 288 (1990), 133–160.CrossRefGoogle Scholar
[9]Milnor, J.. Morse theory. Ann. Math. Studies 51 Princeton University Press: Princeton, 1963.Google Scholar
[10]Nash, J.. The embedding problem for Riemannian manifolds. Ann. of Math. 63 (1956), 20–63.CrossRefGoogle Scholar
[11]Palais, R. S.. Morse theory on Hilbert manifolds. Topology 2 (1963), 299–340.CrossRefGoogle Scholar
[12]Rabinowitz, P. H.. Minimax methods in critical point theory with applications to differential equations. CBMS Reg. Conf. Ser. 65 Amer. Math. Soc.: Providence, 1986.CrossRefGoogle Scholar
[13]Rabinowitz, P. H.. Homoclinic orbits for a class of Hamiltonian systems. Proc. R. Soc. Edinburgh 114A (1990), 33–38.Google Scholar
[14]Rabinowitz, P. H. & Tanaka, K.. Some results on connecting orbits for a class of Hamiltonian systems. Math. Z. 206 (1991), 473–199.CrossRefGoogle Scholar
[15]Schwartz, J. T.. Nonlinear Functional Analysis. Gordon and Breach: New York, 1969.Google Scholar
[16]Séré, E.. Existence of infinitely many homoclinic orbits in Hamiltonian systems. Math. Z. 209 (1992), 27–2.CrossRefGoogle Scholar
[17]Tanaka, K.. Homoclinic orbits in a first order superquadratic Hamiltonian system: convergence of subharmonic orbits. J. Diff. Eq. 94 (1991), 315–339.CrossRefGoogle Scholar