Hostname: page-component-cd9895bd7-dk4vv Total loading time: 0 Render date: 2024-12-22T03:27:53.779Z Has data issue: false hasContentIssue false
  • English
  • Français

Mixing for suspension flows over skew-translations and time-changes of quasi-abelian filiform nilflows

Published online by Cambridge University Press:  28 March 2018

DAVIDE RAVOTTI
DAVIDE RAVOTTI*
Affiliation:
School of Mathematics, University of Bristol, University Walk, Bristol BS8 1TW, UK email davide.ravotti@bristol.ac.uk
Get access Rights & Permissions [Opens in a new window]

Abstract

We consider suspension flows over uniquely ergodic skew-translations on a 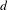$d$-dimensional torus 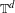$\mathbb{T}^{d}$ for 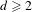$d\geq 2$. We prove that there exists a set 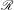$\mathscr{R}$ of smooth functions, which is dense in the space 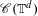$\mathscr{C}(\mathbb{T}^{d})$ of continuous functions, such that every roof function in 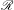$\mathscr{R}$ which is not cohomologous to a constant induces a mixing suspension flow. We also construct a dense set of mixing examples which is explicitly described in terms of their Fourier coefficients. In the language of nilflows on nilmanifolds, our result implies that, for every uniquely ergodic nilflow on a quasi-abelian filiform nilmanifold, there exists a dense subspace of smooth time-changes in which mixing occurs if and only if the time-change is not cohomologous to a constant. This generalizes a theorem by Avila, Forni and Ulcigrai [Mixing for time-changes of Heisenberg nilflows. J. Differential Geom.89(3) (2011), 369–410] for the classical Heisenberg group.

Type
Original Article
Information
Ergodic Theory and Dynamical Systems , Volume 39 , Issue 12 , December 2019 , pp. 3407 - 3436
Copyright
© Cambridge University Press, 2018 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Avila, A., Forni, G. and Ulcigrai, C.. Mixing for time-changes of Heisenberg nilflows. J. Differential Geom. 89(3) (2011), 369–410.Google Scholar
Choudary, A. D. R. and Niculescu, C.. Real Analysis on Intervals. Springer, India, New Delhi, 2014.Google Scholar
Corwin, L. and Greenleaf, F. P.. Representations of Nilpotent Lie Groups and Their Applications. Vol. 1, Part 1, Basic Theory and Examples. Cambridge University Press, Cambridge, 2004.Google Scholar
Einsiedler, M. and Ward, T.. Ergodic Theory (Graduate Texts in Mathematics, 259) . Springer, London, 2011.Google Scholar
Fayad, B. R.. Analytic mixing reparametrizations of irrational flows. Ergod. Th. & Dynam. Sys. 22(2) (2002), 437–468.Google Scholar
Flaminio, L. and Forni, G.. Equidistribution of nilflows and applications to theta sums. Ergod. Th. & Dynam. Sys. 26(2) (2006), 409–433.Google Scholar
Forni, G. and Ulcigrai, C.. Time-changes of horocycle flows. J. Mod. Dyn. 6(2) (2012), 251–273.Google Scholar
Furstenberg, H.. Strict ergodicity and transformation of the torus. Amer. J. Math. 83(4) (1961), 573–601.Google Scholar
Furstenberg, H.. Recurrence in Ergodic Theory and Combinatorial Number Theory. Princeton University Press, Princeton, NJ, 1981.Google Scholar
Gallot, S., Hulin, D. and Lafontaine, J.. Riemannian Geometry. Springer, Berlin, 2004.Google Scholar
Katok, A.. Combinatorial Constructions in Ergodic Theory and Dynamics (University Lecture Series, 30) . American Mathematical Society, Providence, RI, 2003.Google Scholar
Marcus, B.. Ergodic properties of horocycle flows for surfaces of negative curvature. Ann. of Math. (2) 105(1) (1977), 81–105.Google Scholar
Ravotti, D.. Quantitative mixing for locally Hamiltonian flows with saddle loops on compact surfaces. Ann. Henri Poincaré 18(12) (2017), 3815–3861.Google Scholar
Simonelli, L. D.. Absolutely continuous spectrum for parabolic flows/maps. Discrete Contin. Dyn. Syst. 38(1) (2018), 263–292.Google Scholar
Sinai, Ya. G. and Khanin, K. M.. Mixing for some classes of special flows over rotations of the circle. Funct. Anal. Appl. 26(3) (1992), 155–169.Google Scholar
Tiedra de Aldecoa, R.. Spectral analysis of time-changes of horocycle flows. J. Mod. Dyn. 6(2) (2012), 275–285.Google Scholar
Ulcigrai, C.. Mixing of asymmetric logarithmic suspension flows over interval exchange transformations. Ergod. Th. & Dynam. Sys. 27(3) (2007), 991–1035.Google Scholar