Article contents
A link between topological entropy and Lyapunov exponents
Published online by Cambridge University Press: 20 June 2017
Abstract
We show that a 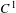 $C^{1}$-generic non-partially hyperbolic symplectic diffeomorphism
$C^{1}$-generic non-partially hyperbolic symplectic diffeomorphism 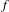 $f$ has topological entropy equal to the supremum of the sum of the positive Lyapunov exponents of its hyperbolic periodic points. Moreover, we also prove that
$f$ has topological entropy equal to the supremum of the sum of the positive Lyapunov exponents of its hyperbolic periodic points. Moreover, we also prove that 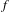 $f$ has topological entropy approximated by the topological entropy of
$f$ has topological entropy approximated by the topological entropy of 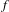 $f$ restricted to basic hyperbolic sets. In particular, the topological entropy map is lower semicontinuous in a
$f$ restricted to basic hyperbolic sets. In particular, the topological entropy map is lower semicontinuous in a 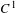 $C^{1}$-generic set of symplectic diffeomorphisms far from partial hyperbolicity.
$C^{1}$-generic set of symplectic diffeomorphisms far from partial hyperbolicity.
- Type
- Original Article
- Information
- Copyright
- © Cambridge University Press, 2017
References
- 1
- Cited by




