Hostname: page-component-848d4c4894-4rdrl Total loading time: 0 Render date: 2024-07-05T04:32:01.606Z Has data issue: false hasContentIssue false
  • English
  • Français

K-property for Maharam extensions of non-singular Bernoulli and Markov shifts

Published online by Cambridge University Press:  05 April 2018

ALEXANDRE I. DANILENKO  and
MARIUSZ LEMAŃCZYK
ALEXANDRE I. DANILENKO
Affiliation:
Institute for Low Temperature Physics & Engineering of National Academy of Sciences of Ukraine, 47 Nauky Avenue, Kharkiv, 61103, Ukraine email alexandre.danilenko@gmail.com
MARIUSZ LEMAŃCZYK
Affiliation:
Faculty of Mathematics and Computer Science, Nicolaus Copernicus University, ul. Chopina 12/18, 87-100 Toruń, Poland email mlem@mat.umk.pl
Get access Rights & Permissions [Opens in a new window]

Abstract

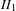It is shown that each conservative non-singular Bernoulli shift is either of type $\mathit{II}_{1}$ or $\mathit{III}_{1}$. Moreover, in the latter case the corresponding Maharam extension of the shift is a $K$-automorphism. This extends earlier results obtained by Kosloff for equilibrial shifts. Non-equilibrial shifts of type 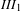$\mathit{III}_{1}$ are constructed. We further generalize (partly) the main results to non-singular Markov shifts.

Type
Original Article
Information
Ergodic Theory and Dynamical Systems , Volume 39 , Issue 12 , December 2019 , pp. 3292 - 3321
Copyright
© Cambridge University Press, 2018 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Aaronson, J.. Rational eregodicity and a metric invariant for Markov shifts. Israel J. Math. 27 (1977), 93–123.Google Scholar
Araki, H. and Woods, E. J.. A classification of factors. Publ. RIMS Kyoto Univ. Ser. A 3 (1968), 51–130.Google Scholar
Brown, G. and Dooley, A. H.. Ergodic measures are of weak product type. Math. Proc. Cambridge Philos. Soc. 98 (1985), 129–145.Google Scholar
Brown, G., Dooley, A. H. and Lake, J.. On the Krieger–Araki–Woods ratio set. Tohôku Math. J. 47 (1995), 1–13.Google Scholar
Choksi, J. R., Hawkins, J. M. and Prasad, V. S.. Abelian cocycles for nonsingular ergodic transformations and the genericity of type III 1 transformations. Monatsh. Math. 103 (1987), 187–205.Google Scholar
Connes, A. and Woods, E. J.. Approximately transitive flows and ITPFI factors. Ergod. Th. & Dynam. Sys. 5 (1985), 203–236.Google Scholar
Dajani, K. and Hawkins, J.. Examples of natural extensions of nonsingular endomorphisms. Proc. Amer. Math. Soc. 120 (1994), 1211–1217.Google Scholar
Danilenko, A. I. and Silva, C. E.. Ergodic theory: non-singular transformations. Mathematics of Complexity and Dynamical Systems. Springer, New York, 2012, pp. 329–356.Google Scholar
Dooley, A. N., Klemes, I. and Quas, A. N.. Product and Markov measures of type III . J. Austral. Math. Soc. 64 (1998), 84–110.Google Scholar
Dooley, A. N. and Mortiss, G.. The critical dimensions of Hamachi shifts. Tohoku Math. J. 59 (2007), 57–66.Google Scholar
Eigen, S. and Silva, C. E.. A structure theorem for n-to-1 nonsingular endomorphisms and existence of non-recurrent measures. J. Lond. Math. Soc. 40 (1989), 441–451.Google Scholar
Feldman, J. and Moore, C. C.. Ergodic equivalence relations, cohomology and von Neumann algebras, I . Trans. Amer. Math. Soc. 234 (1977), 289–324.Google Scholar
Fell, J. M.. A Hausdorff topology for the closed subsets of a locally compact non-Hausdorff space. Proc. Amer. Math. Soc. 13 (1962), 472–476.Google Scholar
Hamachi, T.. On a Bernoulli shift with non-identical factor measures. Ergod. Th. & Dynam. Sys. 1 (1981), 273–284.Google Scholar
Hamachi, T. and Osikawa, M.. Ergodic groups of automorphisms and Krieger’s theorems. Seminar on Mathematical Science of Keio University, Department of Mathematics, Yokohama, 1981, no. 3, pp. 1–113.Google Scholar
Hawkins, J. M.. Amenable relations for endomorphisms. Trans. Amer. Math. Soc. 343 (1994), 169–191.Google Scholar
Kakutani, S.. On equivalence of infinite product measures. Ann. of Math. (2) 49 (1948), 214–224.Google Scholar
Kosloff, Z.. On a type III 1 Bernoulli shift. Ergod. Th. & Dynam. Sys. 31 (2011), 1727–1743.Google Scholar
Kosloff, Z.. On the K property for Maharam extensions of Bernoulli shifts and a question of Krengel. Israel J. Math. 199 (2014), 485–506.Google Scholar
Krengel, U.. Transformations Without Finite Invariant Measure Have Strong Generators (Lecture Notes in Mathematics, 160) . Springer, New York, 1970, pp. 133–157.Google Scholar
Lodkin, A. A.. Absolute continuity of measures corresponding to Markov processes with discrete time. Teor. Veroyatnost. i Primenen. 16 (1971), 703–707 (Russian).Google Scholar
Osikawa, M.. Ergodic properties of product type odometers. Lect. Notes Math. 1299 (1988), 404–414.Google Scholar
Parry, W.. Ergodic and spectral analysis of certain infinite measure preserving transformations. Proc. Amer. Math. Soc. 16 (1965), 960–966.Google Scholar
Rudolph, D. J.. The second centralizer of a Bernoulli shift is just its powers. Israel J. Math. 29 (1978), 167–178.Google Scholar
Schmidt, K.. Cocycles on Ergodic Transformation Groups (MacMillan Lectures in Mathematics, 1) . MacMillan, India, 1977.Google Scholar
Silva, C. E.. On 𝜇-recurrent nonsingular endomorphisms. Israel J. Math. 61 (1988), 1–13.Google Scholar
Silva, C. E. and Thieullen, P.. A skew product entropy for nonsingular transformations. J. Lond. Math. Soc. 52 (1995), 497–516.Google Scholar