Hostname: page-component-76fb5796d-5g6vh Total loading time: 0 Render date: 2024-04-27T04:11:29.162Z Has data issue: false hasContentIssue false
  • English
  • Français

Invariant Jordan curves of Sierpiński carpet rational maps

Published online by Cambridge University Press:  09 September 2016

YAN GAO ,
PETER HAÏSSINSKY ,
DANIEL MEYER  and
JINSONG ZENG
YAN GAO
Affiliation:
Mathematical School of Sichuan University, 610065, PR China email gyan@scu.edu.cn
PETER HAÏSSINSKY
Affiliation:
Université d’Aix-Marseille, Institut de Mathématiques de Marseille (I2M), 39, rue Frédéric Joliot Curie 13453, Marseille Cedex 13, France email phaissin@math.univ-toulouse.fr
DANIEL MEYER
Affiliation:
Department of Mathematics and Statistics, PO Box 35, FI-40014 University of Jyväskylä, Finland email dmeyermail@gmail.com
JINSONG ZENG
Affiliation:
Academy of Mathematics and Systems Science, Chinese Academy of Sciences, Beijing 100190, PR China email zeng.jinsong@amss.ac.cn
Get access Rights & Permissions [Opens in a new window]

Abstract

In this paper, we prove that if 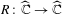$R:\widehat{\mathbb{C}}\rightarrow \widehat{\mathbb{C}}$ is a postcritically finite rational map with Julia set homeomorphic to the Sierpiński carpet, then there is an integer 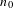$n_{0}$, such that, for any 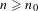$n\geq n_{0}$, there exists an 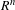$R^{n}$-invariant Jordan curve 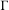$\unicode[STIX]{x1D6E4}$ containing the postcritical set of $R$.

Type
Original Article
Information
Ergodic Theory and Dynamical Systems , Volume 38 , Issue 2 , April 2018 , pp. 583 - 600
Copyright
© Cambridge University Press, 2016 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bernard, J.. Dynamique des perturbations d’un exemple de Lattès. PhD Thesis, Université de Paris-Sud, Orsay, 1994.Google Scholar
Bonk, M., Lyubich, M. and Merenkov, S.. Quasisymmetries of Sierpiński carpet Julia sets. Preprint, 2013.Google Scholar
Bonk, M. and Meyer, D.. Expanding Thurston maps. Available at https://sites.google.com/site/dmeyersite/publications.Google Scholar
Cannon, J. W., Floyd, W. J., Kenyon, R. and Parry, W. R.. Constructing rational maps from subdivision rules. Conform. Geom. Dyn. 7 (2003), 76–102 (electronic).Google Scholar
Cannon, J. W., Floyd, W. J. and Parry, W. R.. Constructing subdivision rules from rational maps. Conform. Geom. Dyn. 11 (2007), 128–136 (electronic).Google Scholar
Cordwell, K., Gilbertson, S., Nuechterlein, N., Pilgrim, K. M. and Pinella, S.. On the classification of critically fixed rational maps. Conform. Geom. Dyn. 19 (2015), 51–94 (electronic).Google Scholar
Daverman, R. J.. Decompositions of Manifolds (Pure and Applied Mathematics, 124) . Academic Press, Orlando, FL, 1986.Google Scholar
Devaney, R. L.. Singular perturbations of complex polynomials. Bull. Amer. Math. Soc. (N.S.) 50(3) (2013), 391–429.Google Scholar
Douady, A. and Hubbard, J.. Etude Dynamique des Polynomes Complexes, I, II. Publications Mathématiques d’Orsay, Université de Paris-Sud, Départment de Mathématiques, Orsay, 1984/5.Google Scholar
Epstein, A.. Bounded hyperbolic components of quadratic rational maps. Ergod. Th. & Dynam. Sys. 20(3) (2000), 727–748.CrossRefGoogle Scholar
Haïssinsky, P. and Pilgrim, K. M.. Coarse expanding conformal dynamics. Astérisque 325 (2009), viii + 139.Google Scholar
Lodge, R., Mikulich, Y. and Schleicher, D.. Combinatorial properties of Newton maps. Preprint, 2015, arXiv:1510.02761.Google Scholar
Lodge, R., Mikulich, Y. and Schleicher, D.. A classification of postcritically finite Newton maps. Preprint, 2015, arXiv:1510.02771.Google Scholar
McMullen, C. T.. The classification of conformal dynamical systems. Current Developments in Mathematics, 1995 (Cambridge, MA). International Press, Cambridge, MA, 1994, pp. 323–360.Google Scholar
McMullen, C. T.. Automorphisms of rational maps. Holomorphic Functions and Moduli I (Mathematical Sciences Research Institute Publications, 10) . Springer, New York, 1988, pp. 31–60.Google Scholar
Milnor, J.. Geometry and dynamics of quadratic rational maps. Experiment. Math. 2(1) (1993), 37–83 With an appendix by the author and Tan Lei.CrossRefGoogle Scholar
Milnor, J.. Dynamics in One Complex Variable (Introductory Lectures) . Friedr. Vieweg & Sohn, Braunschweig, 1999.Google Scholar
Rees, M.. Views of parameter space: Topographer and Resident. Astérisque 288 (2003), vi+418.Google Scholar
Rees, M.. Persistent Markov partitions for rational maps. Preprint, 2013, arXiv:1306.6166.Google Scholar
Rosetti, B.. Sur la détermination des fractions rationnelles postcritiquement finies par des graphes planaires finis. PhD Thesis, Université Paul Sabatier, 2015.Google Scholar
Whyburn, G. T.. Topological characterization of the Sierpiński curve. Fund. Math. 45 (1958), 320–324.CrossRefGoogle Scholar
Whyburn, G. T.. Analytic Topology (American Mathematical Society Colloquium Publications, XXVIII) . American Mathematical Society, Providence, RI, 1963.Google Scholar
Wittner, B.. On the deformation loci of rational maps of degree two. PhD Thesis, Cornell University, 1988.Google Scholar