Article contents
Host–Kra theory for 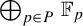 $\bigoplus _{p\in P}{\mathbb {F}}_p$-systems and multiple recurrence
$\bigoplus _{p\in P}{\mathbb {F}}_p$-systems and multiple recurrence
Published online by Cambridge University Press: 25 October 2021
Abstract
Let
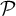 $\mathcal {P}$
be an (unbounded) countable multiset of primes (that is, every prime may appear multiple times) and let
$\mathcal {P}$
be an (unbounded) countable multiset of primes (that is, every prime may appear multiple times) and let
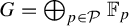 $G=\bigoplus _{p\in \mathcal {P}}\mathbb {F}_p$
. We develop a Host–Kra structure theory for the universal characteristic factors of an ergodic G-system. More specifically, we generalize the main results of Bergelson, Tao and Ziegler [An inverse theorem for the uniformity seminorms associated with the action of
$G=\bigoplus _{p\in \mathcal {P}}\mathbb {F}_p$
. We develop a Host–Kra structure theory for the universal characteristic factors of an ergodic G-system. More specifically, we generalize the main results of Bergelson, Tao and Ziegler [An inverse theorem for the uniformity seminorms associated with the action of
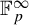 $\mathbb {F}_p^\infty $
. Geom. Funct. Anal. 19(6) (2010), 1539–1596], who studied these factors in the special case
$\mathbb {F}_p^\infty $
. Geom. Funct. Anal. 19(6) (2010), 1539–1596], who studied these factors in the special case
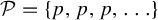 $\mathcal {P}=\{p,p,p,\ldots \}$
for some fixed prime p. As an application we deduce a Khintchine-type recurrence theorem in the flavor of Bergelson, Tao and Ziegler [Multiple recurrence and convergence results associated to
$\mathcal {P}=\{p,p,p,\ldots \}$
for some fixed prime p. As an application we deduce a Khintchine-type recurrence theorem in the flavor of Bergelson, Tao and Ziegler [Multiple recurrence and convergence results associated to
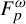 $F_p^\omega $
-actions. J. Anal. Math. 127 (2015), 329–378] and Bergelson, Host and Kra [Multiple recurrence and nilsequences. Invent. Math. 160(2) (2005), 261–303, with an appendix by I. Ruzsa].
$F_p^\omega $
-actions. J. Anal. Math. 127 (2015), 329–378] and Bergelson, Host and Kra [Multiple recurrence and nilsequences. Invent. Math. 160(2) (2005), 261–303, with an appendix by I. Ruzsa].
MSC classification
- Type
- Original Article
- Information
- Copyright
- © The Author(s), 2021. Published by Cambridge University Press
References
REFERENCES
- 2
- Cited by





